En electromagnetismo , una corriente de Foucault (también llamada corriente de Foucault ) es un bucle de corriente eléctrica inducido dentro de los conductores por un campo magnético cambiante en el conductor de acuerdo con la ley de inducción de Faraday o por el movimiento relativo de un conductor en un campo magnético. Las corrientes de Foucault fluyen en bucles cerrados dentro de los conductores, en planos perpendiculares al campo magnético. Pueden ser inducidas dentro de conductores estacionarios cercanos por un campo magnético variable en el tiempo creado por un electroimán de CA o un transformador , por ejemplo, o por el movimiento relativo entre un imán y un conductor cercano. La magnitud de la corriente en un bucle dado es proporcional a la fuerza del campo magnético, el área del bucle y la tasa de cambio de flujo , e inversamente proporcional a la resistividad del material. Cuando se grafican, estas corrientes circulares dentro de una pieza de metal se parecen vagamente a remolinos o torbellinos en un líquido.
Según la ley de Lenz , una corriente de Foucault crea un campo magnético que se opone al cambio en el campo magnético que la creó y, por lo tanto, las corrientes de Foucault reaccionan contra la fuente del campo magnético. Por ejemplo, una superficie conductora cercana ejercerá una fuerza de arrastre sobre un imán en movimiento que se opone a su movimiento, debido a las corrientes de Foucault inducidas en la superficie por el campo magnético en movimiento. Este efecto se emplea en los frenos de corrientes de Foucault que se utilizan para detener rápidamente las herramientas eléctricas giratorias cuando se apagan. La corriente que fluye a través de la resistencia del conductor también disipa energía en forma de calor en el material. Por lo tanto, las corrientes de Foucault son una causa de pérdida de energía en inductores de corriente alterna (CA) , transformadores , motores y generadores eléctricos y otra maquinaria de CA, que requieren una construcción especial, como núcleos magnéticos laminados o núcleos de ferrita para minimizarlas. Las corrientes de Foucault también se utilizan para calentar objetos en hornos y equipos de calentamiento por inducción , y para detectar grietas y fallas en piezas metálicas utilizando instrumentos de prueba de corrientes de Foucault .
El término corriente de Foucault proviene de corrientes análogas observadas en el agua en la dinámica de fluidos , que causan áreas localizadas de turbulencia conocidas como remolinos que dan lugar a vórtices persistentes. De manera algo análoga, las corrientes de Foucault pueden tardar un tiempo en acumularse y pueden persistir durante mucho tiempo en los conductores debido a su inductancia.
El primero en observar corrientes de Foucault fue François Arago (1786-1853), presidente del Consejo de Ministros de la Segunda República Francesa durante el breve período del 10 de mayo al 24 de junio de 1848 (equivalente al cargo actual de Primer Ministro francés), que también era matemático, físico y astrónomo. En 1824 observó lo que se ha llamado magnetismo rotatorio y que la mayoría de los cuerpos conductores podían magnetizarse; estos descubrimientos fueron completados y explicados por Michael Faraday (1791-1867).
En 1834, Emil Lenz formuló la ley de Lenz , que dice que la dirección del flujo de corriente inducida en un objeto será tal que su campo magnético se opondrá al cambio de flujo magnético que causó el flujo de corriente. Las corrientes de Foucault producen un campo secundario que cancela una parte del campo externo y hace que parte del flujo externo evite el conductor.
El descubrimiento de las corrientes parásitas se atribuye al físico francés Léon Foucault (1819-1868). En septiembre de 1855, descubrió que la fuerza necesaria para la rotación de un disco de cobre se hace mayor cuando se hace girar con su borde entre los polos de un imán, calentándose al mismo tiempo el disco por la corriente parásita inducida en el metal. El primer uso de las corrientes parásitas para ensayos no destructivos se produjo en 1879, cuando David E. Hughes utilizó los principios para realizar ensayos de clasificación metalúrgica.
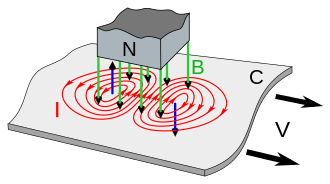
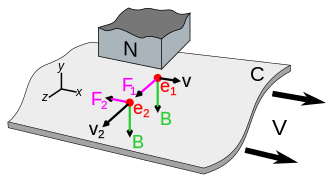
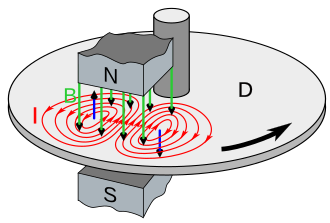
Un imán induce corrientes eléctricas circulares en una lámina metálica que se mueve a través de su campo magnético. Observa el diagrama de la derecha. Muestra una lámina metálica (C) que se mueve hacia la derecha con velocidad v bajo un imán estacionario. El campo magnético ( B , flechas verdes ) del polo norte N del imán pasa hacia abajo a través de la lámina. Como el metal se está moviendo, el flujo magnético a través de un área dada de la lámina está cambiando. En la parte de la lámina que se mueve bajo el borde delantero del imán (lado izquierdo), el campo magnético a través de un punto dado en la lámina aumenta a medida que se acerca al imán .dB/es > 0 . Según la ley de inducción de Faraday , esto crea un campo eléctrico circular en la lámina en sentido antihorario alrededor de las líneas de campo magnético. Este campo induce un flujo de corriente eléctrica en sentido antihorario ( I , rojo ) en la lámina. Esta es la corriente de Foucault. En la parte de la lámina debajo del borde posterior del imán (lado derecho), el campo magnético a través de un punto dado en la lámina disminuye a medida que se aleja del imán, dB/es < 0 , induciendo una segunda corriente de Foucault en el sentido de las agujas del reloj en la lámina.
Otra forma equivalente de entender la corriente es ver que los portadores de carga libres ( electrones ) en la lámina metálica se mueven con la lámina hacia la derecha, por lo que el campo magnético ejerce una fuerza lateral sobre ellos debido a la fuerza de Lorentz . Dado que la velocidad v de las cargas es hacia la derecha y el campo magnético B se dirige hacia abajo, de la regla de la mano derecha la fuerza de Lorentz sobre las cargas positivas F = q ( v × B ) es hacia la parte trasera del diagrama (hacia la izquierda cuando se mira en la dirección del movimiento v ). Esto provoca una corriente I hacia la parte trasera debajo del imán, que circula a través de partes de la lámina fuera del campo magnético, en el sentido de las agujas del reloj hacia la derecha [ cita requerida ] y en el sentido contrario a las agujas del reloj hacia la izquierda, hacia el frente del imán nuevamente. Los portadores de carga móviles en el metal, los electrones , en realidad tienen una carga negativa ( q < 0 ) por lo que su movimiento es opuesto en dirección a la corriente convencional mostrada.
El campo magnético del imán, que actúa sobre los electrones que se desplazan lateralmente bajo el imán, ejerce entonces una fuerza de Lorentz dirigida hacia atrás, en sentido opuesto a la velocidad de la lámina metálica. Los electrones, al colisionar con los átomos de la red metálica, transfieren esta fuerza a la lámina, ejerciendo sobre ella una fuerza de arrastre proporcional a su velocidad. La energía cinética que se consume para vencer esta fuerza de arrastre se disipa en forma de calor por las corrientes que fluyen a través de la resistencia del metal, de modo que el metal se calienta bajo el imán.
Debido a la ley circuital de Ampère, cada una de las corrientes circulares en la lámina crea un campo magnético contrario ( flechas azules ). Otra forma de entender la fuerza de arrastre es ver que debido a la ley de Lenz, los campos contrarios se oponen al cambio en el campo magnético a través de la lámina. En el borde delantero del imán (lado izquierdo), por la regla de la mano derecha, la corriente en sentido antihorario crea un campo magnético que apunta hacia arriba, oponiéndose al campo del imán, causando una fuerza repulsiva entre la lámina y el borde delantero del imán. Por el contrario, en el borde trasero (lado derecho) , la corriente en el sentido de las agujas del reloj causa un campo magnético que apunta hacia abajo, en la misma dirección que el campo del imán, creando una fuerza atractiva entre la lámina y el borde trasero del imán. Ambas fuerzas se oponen al movimiento de la lámina.
Las corrientes de Foucault en conductores de resistividad distinta de cero generan calor y fuerzas electromagnéticas. El calor se puede utilizar para el calentamiento por inducción . Las fuerzas electromagnéticas se pueden utilizar para la levitación, la creación de movimiento o para dar un fuerte efecto de frenado . Las corrientes de Foucault también pueden tener efectos indeseables, por ejemplo, la pérdida de potencia en los transformadores . En esta aplicación, se minimizan con placas delgadas, mediante laminación de conductores u otros detalles de la forma del conductor.
Las corrientes de Foucault autoinducidas son responsables del efecto pelicular en los conductores. [1] Este último se puede utilizar para pruebas no destructivas de materiales para características geométricas, como microfisuras. [2] Un efecto similar es el efecto de proximidad , que es causado por corrientes de Foucault inducidas externamente. [3]
Un objeto o parte de un objeto experimenta una intensidad y dirección de campo constantes en las que todavía hay movimiento relativo del campo y del objeto (por ejemplo, en el centro del campo en el diagrama), o campos inestables en los que las corrientes no pueden circular debido a la geometría del conductor. En estas situaciones, las cargas se acumulan sobre el objeto o dentro de él y producen potenciales eléctricos estáticos que se oponen a cualquier corriente adicional. Las corrientes pueden estar inicialmente asociadas con la creación de potenciales estáticos, pero estos pueden ser transitorios y pequeños.

Las corrientes de Foucault generan pérdidas resistivas que transforman algunas formas de energía, como la energía cinética, en calor. Este calentamiento Joule reduce la eficiencia de los transformadores de núcleo de hierro y los motores eléctricos y otros dispositivos que utilizan campos magnéticos cambiantes. Las corrientes de Foucault se minimizan en estos dispositivos seleccionando materiales de núcleo magnético que tengan baja conductividad eléctrica (por ejemplo, ferritas o polvo de hierro mezclado con resina ) o utilizando láminas delgadas de material magnético, conocidas como laminaciones . Los electrones no pueden cruzar el espacio aislante entre las laminaciones y, por lo tanto, no pueden circular en arcos amplios. Las cargas se reúnen en los límites de las laminaciones, en un proceso análogo al efecto Hall , produciendo campos eléctricos que se oponen a cualquier acumulación adicional de carga y, por lo tanto, suprimen las corrientes de Foucault. Cuanto menor sea la distancia entre las laminaciones adyacentes (es decir, cuanto mayor sea el número de laminaciones por unidad de área, perpendicular al campo aplicado), mayor será la supresión de las corrientes de Foucault.
Sin embargo, la conversión de energía de entrada en calor no siempre es indeseable, ya que existen algunas aplicaciones prácticas. Una de ellas es la de los frenos de algunos trenes, conocidos como frenos de corrientes parásitas . Durante el frenado, las ruedas metálicas se exponen a un campo magnético procedente de un electroimán, lo que genera corrientes parásitas en las ruedas. Esta corriente parásita se forma por el movimiento de las ruedas. Por tanto, según la ley de Lenz , el campo magnético formado por la corriente parásita se opondrá a su causa. Por tanto, la rueda se enfrentará a una fuerza que se opone al movimiento inicial de la rueda. Cuanto más rápido giran las ruedas, más fuerte es el efecto, lo que significa que a medida que el tren reduce la velocidad, la fuerza de frenado se reduce, lo que produce un movimiento de frenado suave.
El calentamiento por inducción utiliza corrientes de Foucault para calentar objetos metálicos.
Bajo ciertas suposiciones (material uniforme, campo magnético uniforme, sin efecto pelicular , etc.) la potencia perdida debido a corrientes de Foucault por unidad de masa para una lámina delgada o alambre se puede calcular a partir de la siguiente ecuación: [4] donde
Esta ecuación sólo es válida en las llamadas condiciones cuasiestáticas, donde la frecuencia de magnetización no produce el efecto pelicular , es decir, la onda electromagnética penetra completamente en el material.
En campos que cambian muy rápidamente, el campo magnético no penetra completamente en el interior del material. Este efecto pelicular invalida la ecuación anterior. Sin embargo, en cualquier caso, un aumento de frecuencia del mismo valor de campo siempre aumentará las corrientes parásitas, incluso con una penetración de campo no uniforme. [ cita requerida ]
La profundidad de penetración de un buen conductor se puede calcular a partir de la siguiente ecuación: [5] donde δ es la profundidad de penetración (m), f es la frecuencia (Hz), μ es la permeabilidad magnética del material (H/m) y σ es la conductividad eléctrica del material (S/m).
La derivación de una ecuación útil para modelar el efecto de las corrientes de Foucault en un material comienza con la forma magnetostática diferencial de la Ley de Ampère , [6] que proporciona una expresión para el campo magnetizante H que rodea una densidad de corriente J :
Tomando el rizo en ambos lados de esta ecuación y luego utilizando una identidad de cálculo vectorial común para el rizo del rizo, se obtiene
De la ley de Gauss para el magnetismo , ∇ ⋅ H = 0 , por lo que
Utilizando la ley de Ohm , J = σ E , que relaciona la densidad de corriente J con el campo eléctrico E en términos de la conductividad de un material σ , y asumiendo una conductividad homogénea isótropa, la ecuación se puede escribir como
Utilizando la forma diferencial de la ley de Faraday , ∇ × E = − ∂ B/∂ , esto da
Por definición, B = μ 0 ( H + M ) , donde M es la magnetización del material y μ 0 es la permeabilidad al vacío . Por lo tanto, la ecuación de difusión es
Los frenos por corrientes de Foucault utilizan la fuerza de arrastre creada por las corrientes de Foucault como freno para frenar o detener objetos en movimiento. Como no hay contacto con una zapata o tambor de freno, no hay desgaste mecánico. Sin embargo, un freno por corrientes de Foucault no puede proporcionar un par de "retención" y, por lo tanto, se puede utilizar en combinación con frenos mecánicos, por ejemplo, en grúas aéreas. Otra aplicación es en algunas montañas rusas, donde las placas de cobre pesadas que se extienden desde el vagón se mueven entre pares de imanes permanentes muy fuertes. La resistencia eléctrica dentro de las placas provoca un efecto de arrastre análogo a la fricción, que disipa la energía cinética del vagón. La misma técnica se utiliza en los frenos electromagnéticos de los vagones de ferrocarril y para detener rápidamente las cuchillas de las herramientas eléctricas, como las sierras circulares. Al utilizar electroimanes, a diferencia de los imanes permanentes, se puede ajustar la fuerza del campo magnético y, por lo tanto, cambiar la magnitud del efecto de frenado.

En un campo magnético variable, las corrientes inducidas exhiben efectos de repulsión similares a los diamagnéticos. Un objeto conductor experimentará una fuerza de repulsión. Esto puede levantar objetos contra la gravedad, aunque con una entrada de energía continua para reemplazar la energía disipada por las corrientes de Foucault. Un ejemplo de aplicación es la separación de latas de aluminio de otros metales en un separador de corrientes de Foucault . Los metales ferrosos se adhieren al imán y el aluminio (y otros conductores no ferrosos) son expulsados del imán; esto puede separar una corriente de desechos en chatarra ferrosa y no ferrosa.
Con un imán portátil muy potente, como los fabricados con neodimio , se puede observar fácilmente un efecto muy similar al pasar rápidamente el imán sobre una moneda con una pequeña separación. Dependiendo de la fuerza del imán, la identidad de la moneda y la separación entre el imán y la moneda, se puede inducir a que la moneda se empuje ligeramente por delante del imán, incluso si la moneda no contiene elementos magnéticos, como el centavo estadounidense . Otro ejemplo implica dejar caer un imán potente por un tubo de cobre [7] : el imán cae a un ritmo dramáticamente lento.
En un conductor perfecto sin resistencia , las corrientes parásitas superficiales cancelan exactamente el campo dentro del conductor, por lo que ningún campo magnético penetra en el conductor. Dado que no se pierde energía en la resistencia, las corrientes parásitas creadas cuando se acerca un imán al conductor persisten incluso después de que el imán esté estacionario y pueden equilibrar exactamente la fuerza de la gravedad, lo que permite la levitación magnética . Los superconductores también exhiben un fenómeno mecánico cuántico inherente independiente llamado efecto Meissner en el que se expulsan todas las líneas de campo magnético presentes en el material cuando se vuelve superconductor, por lo que el campo magnético en un superconductor siempre es cero.
Utilizando electroimanes con conmutación electrónica comparable al control electrónico de velocidad , es posible generar campos electromagnéticos que se mueven en una dirección arbitraria. Como se describió en la sección anterior sobre frenos de corrientes de Foucault, una superficie conductora no ferromagnética tiende a descansar dentro de este campo móvil. Sin embargo, cuando este campo se mueve, un vehículo puede levitar y propulsarse. Esto es comparable a un maglev pero no está ligado a un riel. [8]
En algunas máquinas expendedoras que funcionan con monedas , se utilizan corrientes parásitas para detectar monedas falsas o slugs . La moneda rueda frente a un imán fijo y las corrientes parásitas reducen su velocidad. La intensidad de las corrientes parásitas, y por lo tanto la desaceleración, depende de la conductividad del metal de la moneda. Los slugs se ralentizan en un grado diferente al de las monedas auténticas, y esto se utiliza para enviarlas a la ranura de rechazo.
Las corrientes de Foucault se utilizan en ciertos tipos de sensores de proximidad para observar la vibración y la posición de los ejes giratorios dentro de sus cojinetes. Esta tecnología fue desarrollada originalmente en la década de 1930 por investigadores de General Electric que utilizaban circuitos de tubos de vacío. A fines de la década de 1950, Donald E. Bently de Bently Nevada Corporation desarrolló versiones de estado sólido . Estos sensores son extremadamente sensibles a desplazamientos muy pequeños, lo que los hace muy adecuados para observar las vibraciones diminutas (del orden de varias milésimas de pulgada) en la turbomaquinaria moderna . Un sensor de proximidad típico utilizado para el monitoreo de vibraciones tiene un factor de escala de 200 mV/mil. [ aclaración necesaria ] El uso generalizado de dichos sensores en la turbomaquinaria ha llevado al desarrollo de estándares industriales que prescriben su uso y aplicación. Ejemplos de dichos estándares son la Norma 670 del Instituto Americano del Petróleo (API) y la ISO 7919.
Un sensor de aceleración Ferraris, también llamado sensor Ferraris, es un sensor sin contacto que utiliza corrientes de Foucault para medir la aceleración relativa. [9] [10] [11]
Las técnicas de corrientes de Foucault se utilizan comúnmente para el examen no destructivo (END) y el monitoreo de condición de una gran variedad de estructuras metálicas, incluidos tubos de intercambiadores de calor , fuselajes de aeronaves y componentes estructurales de aeronaves.
Las corrientes de Foucault son la causa principal del efecto pelicular en los conductores que transportan corriente alterna .
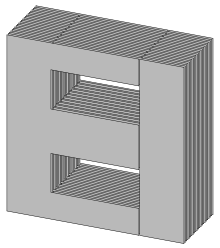
De manera similar, en materiales magnéticos de conductividad finita, las corrientes de Foucault hacen que la mayoría de los campos magnéticos se confinen a sólo un par de profundidades superficiales del material. Este efecto limita el enlace de flujo en inductores y transformadores que tienen núcleos magnéticos .
