Espiral de Arquímedes

Espiral con distancia constante de sí misma

Tres bucles de 360° de un brazo de una espiral de Arquímedes

La espiral de Arquímedes (también conocida como espiral de Arquímedes , espiral aritmética ) es una espiral que recibe su nombre del matemático griego del siglo III a. C. Arquímedes . El término espiral de Arquímedes se utiliza a veces para referirse a la clase más general de espirales de este tipo (véase más abajo), en contraste con la espiral de Arquímedes (la espiral aritmética específica de Arquímedes). Es el lugar geométrico correspondiente a las ubicaciones en el tiempo de un punto que se aleja de un punto fijo con una velocidad constante a lo largo de una línea que gira con velocidad angular constante . De manera equivalente, en coordenadas polares ( r , θ ) se puede describir mediante la ecuación con el número real b . Cambiar el parámetro b controla la distancia entre bucles. $${\displaystyle r=b\cdot \theta }$$

De la ecuación anterior se puede afirmar que la posición de la partícula desde el punto de inicio es proporcional al ángulo θ a medida que transcurre el tiempo.

Arquímedes describió una espiral de este tipo en su libro Sobre las espirales . Conón de Samos era amigo suyo y Pappus afirma que esta espiral fue descubierta por Conón. ^[1]

Derivación de la ecuación general de la espiral

A continuación se utiliza un enfoque físico para comprender el concepto de espirales de Arquímedes.

Supongamos que un objeto puntual se mueve en el sistema cartesiano con una velocidad constante v dirigida paralela al eje x con respecto al plano xy . Sea que en el instante t = 0 el objeto se encontraba en un punto arbitrario ( c , 0, 0) . Si el plano xy gira con una velocidad angular constante ω alrededor del eje z , entonces la velocidad del punto con respecto al eje z puede escribirse como:

El plano xy gira un ángulo ωt (en sentido antihorario) alrededor del origen en el tiempo t . ( c , 0) es la posición del objeto en t = 0 . P es la posición del objeto en el tiempo t , a una distancia de R = vt + c .

$${\displaystyle {\begin{aligned}|v_{0}|&={\sqrt {v^{2}+\omega ^{2}(vt+c)^{2}}}\\v_{x}&=v\cos \omega t-\omega (vt+c)\sin \omega t\\v_{y}&=v\sin \omega t+\omega (vt+c)\cos \omega t\end{aligned}}}$$

Como se muestra en la figura de al lado, tenemos vt + c que representa el módulo del vector de posición de la partícula en cualquier momento t , con v _x y v _y como los componentes de velocidad a lo largo de los ejes x e y, respectivamente.

$${\displaystyle {\begin{aligned}\int v_{x}\,dt&=x\\\int v_{y}\,dt&=y\end{aligned}}}$$

Las ecuaciones anteriores se pueden integrar aplicando integración por partes , lo que da lugar a las siguientes ecuaciones paramétricas:

$${\displaystyle {\begin{aligned}x&=(vt+c)\cos \omega t\\y&=(vt+c)\sin \omega t\end{aligned}}}$$

Al elevar al cuadrado las dos ecuaciones y luego sumarlas (y algunas pequeñas modificaciones), se obtiene la ecuación cartesiana (usando el hecho de que ωt = θ y θ = arctan ⁠ $${\displaystyle {\sqrt {x^{2}+y^{2}}}={\frac {v}{\omega }}\cdot \arctan {\frac {y}{x}}+c}$$y/incógnita⁠ ) ​​o $${\displaystyle \tan \left(\left({\sqrt {x^{2}+y^{2}}}-c\right)\cdot {\frac {\omega }{v}}\right)={\frac {y}{x}}}$$

Su forma polar es $${\displaystyle r={\frac {v}{\omega }}\cdot \theta +c.}$$

Longitud y curvatura del arco

Círculos osculadores de la espiral de Arquímedes, tangentes a la espiral y con la misma curvatura en el punto tangente. La espiral en sí no está dibujada, pero se pueden ver los puntos en los que los círculos están especialmente próximos entre sí.

Dada la parametrización en coordenadas cartesianas la longitud del arco desde θ ₁ hasta θ ₂ es o, equivalentemente: La longitud total desde θ ₁ = 0 hasta θ ₂ = θ es por lo tanto $${\displaystyle f\colon \theta \mapsto (r\,\cos \theta ,r\,\sin \theta )=(b\,\theta \,\cos \theta ,b\,\theta \,\sin \theta )}$$ $${\displaystyle {\frac {b}{2}}\left[\theta \,{\sqrt {1+\theta ^{2}}}+\ln \left(\theta +{\sqrt {1+\theta ^{2}}}\right)\right]_{\theta _{1}}^{\theta _{2}}}$$ $${\displaystyle {\frac {b}{2}}\left[\theta \,{\sqrt {1+\theta ^{2}}}+\operatorname {arsinh} \theta \right]_{\theta _{1}}^{\theta _{2}}.}$$ $${\displaystyle {\frac {b}{2}}\left[\theta \,{\sqrt {1+\theta ^{2}}}+\ln \left(\theta +{\sqrt {1+\theta ^{2}}}\right)\right].}$$

La curvatura viene dada por $${\displaystyle \kappa ={\frac {\theta ^{2}+2}{b\left(\theta ^{2}+1\right)^{\frac {3}{2}}}}}$$

Características

Espiral de Arquímedes representada en un gráfico polar

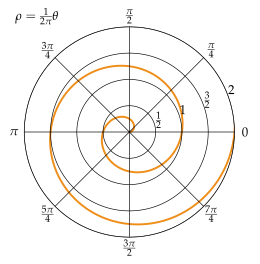
La espiral de Arquímedes tiene la propiedad de que cualquier rayo que parte del origen corta las sucesivas espiras de la espiral en puntos con una distancia de separación constante (igual a 2 πb si θ se mide en radianes ), de ahí el nombre de "espiral aritmética". En cambio, en una espiral logarítmica estas distancias, así como las distancias de los puntos de intersección medidas desde el origen, forman una progresión geométrica .

La espiral de Arquímedes tiene dos brazos, uno para θ > 0 y otro para θ < 0. Los dos brazos están conectados suavemente en el origen. En el gráfico adjunto se muestra solo un brazo. Si tomamos la imagen especular de este brazo a lo largo del eje y obtendremos el otro brazo.

Para un θ grande, un punto se mueve con una aceleración uniforme bien aproximada a lo largo de la espiral de Arquímedes, mientras que la espiral corresponde a las ubicaciones en el tiempo de un punto que se aleja de un punto fijo con una velocidad constante a lo largo de una línea que gira con velocidad angular constante ^[2] (ver la contribución de Mikhail Gaichenkov).

A medida que la espiral de Arquímedes crece, su evoluta se aproxima asintóticamente a un círculo con radio ⁠| en |/ω⁠ .

Espiral de Arquímedes general

A veces se utiliza el término espiral de Arquímedes para el grupo más general de espirales. $${\displaystyle r=a+b\cdot \theta ^{\frac {1}{c}}.}$$

La espiral arquimediana normal se produce cuando c = 1. Otras espirales que entran en este grupo son la espiral hiperbólica ( c = −1 ), la espiral de Fermat ( c = 2 ) y la espiral de Litus ( c = −2 ).

Aplicaciones

Un método para cuadrar el círculo , creado por Arquímedes, utiliza una espiral arquimediana. Arquímedes también demostró cómo se puede utilizar la espiral para trisecar un ángulo . Ambos enfoques flexibilizan las limitaciones tradicionales del uso de la regla y el compás en las demostraciones geométricas de la antigua Grecia. ^[3]

Mecanismo de un compresor scroll

La espiral de Arquímedes tiene una variedad de aplicaciones en el mundo real. Los compresores de espiral , utilizados para comprimir gases, tienen rotores que pueden estar hechos de dos espirales de Arquímedes intercaladas, involutas de un círculo del mismo tamaño que casi se parecen a las espirales de Arquímedes ^[4] o curvas híbridas.

Las espirales de Arquímedes se pueden encontrar en antenas espirales , que pueden funcionar en un amplio rango de frecuencias.

Las bobinas de los resortes de equilibrio de los relojes y las ranuras de los primeros discos de gramófono forman espirales de Arquímedes, lo que hace que las ranuras estén espaciadas de manera uniforme (aunque más tarde se introdujo el espaciado variable entre pistas para maximizar la cantidad de música que se podía cortar en un disco). ^[5]

Pedirle a un paciente que dibuje una espiral de Arquímedes es una forma de cuantificar el temblor humano ; esta información ayuda a diagnosticar enfermedades neurológicas.

Las espirales de Arquímedes también se utilizan en sistemas de proyección de procesamiento de luz digital (DLP) para minimizar el " efecto arco iris ", haciendo que parezca que se muestran múltiples colores al mismo tiempo, cuando en realidad el rojo, el verde y el azul están cambiando de color extremadamente rápido. ^[6] Además, las espirales de Arquímedes se utilizan en microbiología de alimentos para cuantificar la concentración bacteriana a través de un plato espiral. ^[7]

Imagen de Atacama Large Millimeter Array de LL Pegasi

También se utilizan para modelar el patrón que se produce en un rollo de papel o cinta de espesor constante enrollado alrededor de un cilindro. ^{[8] [9]}

Muchas espirales dinámicas (como la espiral de Parker del viento solar o el patrón formado por la rueda de Catalina ) son de Arquímedes. Por ejemplo, la estrella LL Pegasi muestra una espiral de Arquímedes aproximada en las nubes de polvo que la rodean, que se cree que son materia expulsada de la estrella que ha sido conducida a una espiral por otra estrella compañera como parte de un sistema estelar doble. ^[10]

Métodos de construcción

La espiral de Arquímedes no se puede construir con precisión mediante los métodos tradicionales de regla y compás, ya que la espiral aritmética requiere que el radio de la curva se incremente constantemente a medida que se incrementa el ángulo en el origen. Pero una espiral aritmética se puede construir de manera aproximada, con distintos grados de precisión, mediante varios métodos de dibujo manual. Uno de estos métodos utiliza regla y compás; otro método utiliza un compás de cuerda modificado.

La construcción tradicional común utiliza compás y regla para aproximarse a la espiral aritmética. Primero, se construye un círculo grande y su circunferencia se subdivide por 12 diámetros en 12 arcos (de 30 grados cada uno; ver dodecágono regular ). A continuación, el radio de este círculo se subdivide en 12 segmentos unitarios (unidades radiales), y se construye una serie de círculos concéntricos, cada uno con un radio incrementado en una unidad radial. Comenzando con el diámetro horizontal y el círculo concéntrico más interno, se marca el punto donde su radio interseca su circunferencia; luego se pasa al siguiente círculo concéntrico y al siguiente diámetro (moviéndose hacia arriba para construir una espiral en sentido antihorario, o hacia abajo para el sentido horario) para marcar el siguiente punto. Después de que se han marcado todos los puntos, los puntos sucesivos se conectan mediante una línea que se aproxima a la espiral aritmética (o mediante una curva suave de algún tipo; ver Curva Francesa ). Dependiendo del grado de precisión deseado, este método puede mejorarse aumentando el tamaño del círculo exterior grande, haciendo más subdivisiones tanto de su circunferencia como de su radio, aumentando el número de círculos concéntricos (ver Espiral poligonal ). Aproximar la espiral de Arquímedes mediante este método es, por supuesto, una reminiscencia del famoso método de Arquímedes de aproximar π duplicando los lados de polígonos sucesivos (ver Aproximación poligonal de π ).

La construcción con compás y regla de la espiral de Teodoro es otro método simple para aproximar la espiral de Arquímedes.

Un método mecánico para construir la espiral aritmética utiliza un compás de cuerda modificado, donde la cuerda se enrolla y se enrolla (o se desenrolla/desenrolla) alrededor de un pasador central fijo (que no gira), aumentando (o disminuyendo) así la longitud del radio (cuerda) a medida que cambia el ángulo (la cuerda se enrolla alrededor del pasador fijo que no gira). Este método es una forma sencilla de crear una espiral aritmética, que surge naturalmente del uso de un compás de cuerda con un pasador de enrollamiento (no el pivote suelto de un compás de cuerda común). La herramienta de dibujo del compás de cuerda tiene varias modificaciones y diseños, y este método de construcción recuerda a los métodos basados ​​en cuerdas para crear elipses (con dos pasadores fijos).

Otro método mecánico es una variante del anterior método de la brújula de cuerda, que proporciona una mayor precisión y más flexibilidad. En lugar del pasador central y la cuerda de la brújula de cuerda, este dispositivo utiliza un eje no giratorio (columna) con roscas helicoidales (tornillo; véase el tornillo de Arquímedes ) al que se unen dos brazos ranurados: un brazo horizontal está fijado a (se desplaza hacia arriba) las roscas del tornillo del eje vertical en un extremo, y sostiene una herramienta de dibujo en el otro extremo; otro brazo inclinado está fijado en un extremo a la parte superior del eje del tornillo, y está unido por un pasador ajustado de forma suelta en su ranura a la ranura del brazo horizontal. Los dos brazos giran juntos y trabajan en conjunto para producir la espiral aritmética: a medida que el brazo horizontal sube gradualmente por el tornillo, la unión ranurada de ese brazo al brazo inclinado acorta gradualmente el radio de dibujo. El ángulo del brazo inclinado permanece constante en todo momento (traza un cono ), y al establecer un ángulo diferente varía el paso de la espiral. Este dispositivo proporciona un alto grado de precisión, dependiendo de la precisión con la que se mecaniza el dispositivo (mecanizar una rosca helicoidal precisa es un desafío relacionado). Y, por supuesto, el uso de un eje de tornillo en este mecanismo recuerda al tornillo de Arquímedes .

Véase también

• Portal de matemáticas

• El tornillo de Arquímedes  : mecanismo de bombeo de agua
• Espiral de Fermat  : espiral que rodea un área igual por vuelta
• Espiral áurea  : curva autosimilar relacionada con la proporción áurea
• Espiral hiperbólica  – Espiral asintótica a una línea
• Lista de espirales
• Espiral logarítmica  – Curva de crecimiento autosimilar
• Espiral de Teodoro  – Curva poligonal formada por triángulos rectángulos
• Símbolo de triple espiral  : varios símbolos con simetría rotacional triplePages displaying short descriptions of redirect targets

Referencias

1. Bulmer-Thomas, Ivor . "Conón de Samos". Diccionario de biografía científica . Vol. 3. pág. 391.
2. Sloane, N. J. A. (ed.). "Secuencia A091154". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
3. Boyer, Carl B. (1968). Una historia de las matemáticas . Princeton, Nueva Jersey: Princeton University Press. pp. 140–142. ISBN 0-691-02391-3.
4. Sakata, Hirotsugu; Okuda, Masayuki. "Dispositivo de compresión de fluidos con elementos espirales coaxiales" . Consultado el 25 de noviembre de 2006 .
5. Penndorf, Ron. "Desarrollo temprano del LP". Archivado desde el original el 5 de noviembre de 2005. Consultado el 25 de noviembre de 2005 .. Vea el pasaje sobre Variable Groove .
6. Ballou, Glen (2008), Manual para ingenieros de sonido, CRC Press, pág. 1586, ISBN 9780240809694
7. Gilchrist, JE; Campbell, JE; Donnelly, CB; Peeler, JT; Delaney, JM (1973). "Método de placa espiral para la determinación bacteriana". Applied Microbiology . 25 (2): 244–52. doi :10.1128/AEM.25.2.244-252.1973. PMC 380780 . PMID  4632851. 
8. Peressini, Tony (3 de febrero de 2009). "El problema del rollo de papel de Joan" (PDF) . Archivado desde el original (PDF) el 3 de noviembre de 2013. Consultado el 6 de octubre de 2014 .
9. Walser, H.; Hilton, P.; Pedersen, J. (2000). Simetría . Asociación Matemática de Estados Unidos. pág. 27. ISBN 9780883855324. Recuperado el 6 de octubre de 2014 .
10. Kim, Hyosun; Trejo, Alfonso; Liu, Sheng-Yuan; Sahai, Raghvendra; Taam, Ronald E.; Morris, Mark R.; Hirano, Naomi; Hsieh, I-Ta (marzo de 2017). "El patrón nebular a gran escala de un binario de superviento en una órbita excéntrica". Astronomía de la Naturaleza . 1 (3): 0060. arXiv : 1704.00449 . Código Bib : 2017NatAs...1E..60K. doi :10.1038/s41550-017-0060. S2CID  119433782.

Enlaces externos

• Jonathan Matt hace que la espiral de Arquímedes sea interesante - Vídeo: La sorprendente belleza de las matemáticas - Charlas TedX , Green Farms
• Weisstein, Eric W. "Espiral de Arquímedes". MundoMatemático .
• espiral de Arquímedes en PlanetMath .
• Página con aplicación Java para explorar de forma interactiva la espiral de Arquímedes y sus curvas relacionadas
• Exploración en línea mediante JSXGraph (JavaScript)
• Espiral de Arquímedes en "mathcurve"