Diferencial de una función

Noción en cálculo

En cálculo , la diferencial representa la parte principal del cambio en una función con respecto a los cambios en la variable independiente. La diferencial se define por donde es la derivada de f con respecto a , y es una variable real adicional (por lo que es una función de y ). La notación es tal que la ecuación ${\displaystyle y=f(x)}$ ${\displaystyle dy}$ $${\displaystyle dy=f'(x)\,dx,}$$ ${\displaystyle f'(x)}$ ${\displaystyle x}$ ${\displaystyle dx}$ ${\displaystyle dy}$ ${\displaystyle x}$ ${\displaystyle dx}$

$${\displaystyle dy={\frac {dy}{dx}}\,dx}$$

se cumple, donde la derivada se representa en la notación de Leibniz , y esto es consistente con considerar la derivada como el cociente de las diferenciales. También se escribe ${\displaystyle dy/dx}$

$${\displaystyle df(x)=f'(x)\,dx.}$$

El significado preciso de las variables y depende del contexto de la aplicación y del nivel requerido de rigor matemático. El dominio de estas variables puede adquirir un significado geométrico particular si la diferencial se considera como una forma diferencial particular , o un significado analítico si la diferencial se considera como una aproximación lineal al incremento de una función. Tradicionalmente, las variables y se consideran muy pequeñas ( infinitesimales ), y esta interpretación se hace rigurosa en el análisis no estándar . ${\displaystyle dy}$ ${\displaystyle dx}$ ${\displaystyle dx}$ ${\displaystyle dy}$

Historia y uso

La diferencial fue introducida por primera vez a través de una definición intuitiva o heurística por Isaac Newton y ampliada por Gottfried Leibniz , quien pensó en la diferencial  dy como un cambio infinitamente pequeño (o infinitesimal ) en el valor  y de la función, correspondiente a un cambio infinitamente pequeño  dx en el argumento  x de la función . Por esa razón, la tasa instantánea de cambio de y con respecto a x , que es el valor de la derivada de la función, se denota por la fracción

$${\displaystyle {\frac {dy}{dx}}}$$en lo que se denomina la notación de Leibniz para derivadas. El cociente no es infinitamente pequeño, sino que es un número real . ${\displaystyle dy/dx}$

El uso de infinitesimales en esta forma fue ampliamente criticado, por ejemplo, por el famoso panfleto El analista del obispo Berkeley. Augustin-Louis Cauchy (1823) definió la diferencial sin apelar al atomismo de los infinitesimales de Leibniz. ^{[1] [2]} En cambio, Cauchy, siguiendo a d'Alembert , invirtió el orden lógico de Leibniz y sus sucesores: la derivada misma se convirtió en el objeto fundamental, definido como un límite de cocientes de diferencias, y las diferenciales se definieron entonces en términos de él. Es decir, uno era libre de definir la diferencial mediante una expresión en la que y son simplemente nuevas variables que toman valores reales finitos, ^[3] no infinitesimales fijos como lo habían sido para Leibniz. ^[4] ${\displaystyle dy}$ $${\displaystyle dy=f'(x)\,dx}$$ ${\displaystyle dy}$ ${\displaystyle dx}$

Según Boyer (1959, p. 12), el enfoque de Cauchy fue una mejora lógica significativa sobre el enfoque infinitesimal de Leibniz porque, en lugar de invocar la noción metafísica de infinitesimales, las cantidades y ahora podían manipularse exactamente de la misma manera que cualquier otra cantidad real de una manera significativa. El enfoque conceptual general de Cauchy para las diferenciales sigue siendo el estándar en los tratamientos analíticos modernos, ^[5] aunque la última palabra sobre el rigor, una noción completamente moderna del límite, se debió en última instancia a Karl Weierstrass . ^[6] ${\displaystyle dy}$ ${\displaystyle dx}$

En los tratamientos físicos, como los aplicados a la teoría de la termodinámica , todavía prevalece la visión infinitesimal. Courant y John (1999, p. 184) concilian el uso físico de diferenciales infinitesimales con la imposibilidad matemática de los mismos de la siguiente manera. Los diferenciales representan valores finitos distintos de cero que son menores que el grado de precisión requerido para el propósito particular para el que están destinados. Por lo tanto, los "infinitesimales físicos" no necesitan apelar a un infinitesimal matemático correspondiente para tener un sentido preciso.

Tras los avances del siglo XX en el análisis matemático y la geometría diferencial , se hizo evidente que la noción de diferencial de una función podía extenderse de diversas maneras. En el análisis real , es más deseable tratar directamente con la diferencial como la parte principal del incremento de una función. Esto conduce directamente a la noción de que la diferencial de una función en un punto es una funcional lineal de un incremento . Este enfoque permite desarrollar la diferencial (como una función lineal) para una variedad de espacios más sofisticados, dando lugar en última instancia a nociones como la derivada de Fréchet o Gateaux . Del mismo modo, en la geometría diferencial , la diferencial de una función en un punto es una función lineal de un vector tangente (un "desplazamiento infinitamente pequeño"), que la exhibe como una especie de forma única: la derivada exterior de la función. En el cálculo no estándar , las diferenciales se consideran infinitesimales, que pueden ponerse en una base rigurosa (véase diferencial (infinitesimal) ). ${\displaystyle \Delta x}$

Definición

La diferencial de una función en un punto . ${\displaystyle f(x)}$ ${\displaystyle x_{0}}$

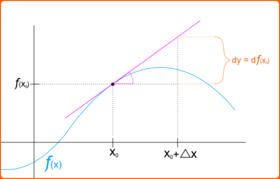
La diferencial se define en los tratamientos modernos del cálculo diferencial de la siguiente manera. ^[7] La ​​diferencial de una función de una sola variable real es la función de dos variables reales independientes y está dada por ${\displaystyle f(x)}$ ${\displaystyle x}$ ${\displaystyle df}$ ${\displaystyle x}$ ${\displaystyle \Delta x}$

$${\displaystyle df(x,\Delta x)\ {\stackrel {\mathrm {def} }{=}}\ f'(x)\,\Delta x.}$$

Se puede suprimir uno o ambos argumentos, es decir, se puede ver o simplemente . Si , la diferencial también se puede escribir como . Como , es convencional escribir de modo que se cumpla la siguiente igualdad: ${\displaystyle df(x)}$ ${\displaystyle df}$ ${\displaystyle y=f(x)}$ ${\displaystyle dy}$ ${\displaystyle dx(x,\Delta x)=\Delta x}$ ${\displaystyle dx=\Delta x}$

$${\displaystyle df(x)=f'(x)\,dx}$$

Esta noción de diferencial es ampliamente aplicable cuando se busca una aproximación lineal a una función, en la que el valor del incremento es suficientemente pequeño. Más precisamente, si es una función diferenciable en , entonces la diferencia en valores de ${\displaystyle \Delta x}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle y}$

$${\displaystyle \Delta y\ {\stackrel {\rm {def}}{=}}\ f(x+\Delta x)-f(x)}$$

satisface

$${\displaystyle \Delta y=f'(x)\,\Delta x+\varepsilon =df(x)+\varepsilon \,}$$

donde el error en la aproximación satisface como . En otras palabras, se tiene la identidad aproximada ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon /\Delta x\rightarrow 0}$ ${\displaystyle \Delta x\rightarrow 0}$

$${\displaystyle \Delta y\approx dy}$$

en la que el error puede hacerse tan pequeño como se desee en relación con restringiendo a que sea suficientemente pequeño; es decir, como . Por esta razón, la diferencial de una función se conoce como la parte principal (lineal) en el incremento de una función: la diferencial es una función lineal del incremento , y aunque el error puede ser no lineal, tiende a cero rápidamente a medida que tiende a cero. ${\displaystyle \Delta x}$ ${\displaystyle \Delta x}$ $${\displaystyle {\frac {\Delta y-dy}{\Delta x}}\to 0}$$ ${\displaystyle \Delta x\rightarrow 0}$ ${\displaystyle \Delta x}$ ${\displaystyle \varepsilon }$ ${\displaystyle \Delta x}$

Diferenciales en varias variables

Siguiendo a Goursat (1904, I, §15), para funciones de más de una variable independiente,

$${\displaystyle y=f(x_{1},\dots ,x_{n}),}$$

La diferencial parcial de y con respecto a cualquiera de las variables  x ₁ es la parte principal del cambio en y resultante de un cambio  dx ₁ en esa variable. La diferencial parcial es, por lo tanto,

$${\displaystyle {\frac {\partial y}{\partial x_{1}}}dx_{1}}$$

que involucra la derivada parcial de y con respecto a  x ₁ . La suma de las diferenciales parciales con respecto a todas las variables independientes es la diferencial total

$${\displaystyle dy={\frac {\partial y}{\partial x_{1}}}dx_{1}+\cdots +{\frac {\partial y}{\partial x_{n}}}dx_{n},}$$

que es la parte principal del cambio en y resultante de los cambios en las variables independientes  x _i .

Más precisamente, en el contexto del cálculo multivariable, siguiendo a Courant (1937b), si f es una función diferenciable, entonces por la definición de diferenciabilidad , el incremento

$${\displaystyle {\begin{aligned}\Delta y&{}~{\stackrel {\mathrm {def} }{=}}~f(x_{1}+\Delta x_{1},\dots ,x_{n}+\Delta x_{n})-f(x_{1},\dots ,x_{n})\\&{}={\frac {\partial y}{\partial x_{1}}}\Delta x_{1}+\cdots +{\frac {\partial y}{\partial x_{n}}}\Delta x_{n}+\varepsilon _{1}\Delta x_{1}+\cdots +\varepsilon _{n}\Delta x_{n}\end{aligned}}}$$

donde los términos de error ε _i  tienden a cero a medida que los incrementos Δ x _i tienden conjuntamente a cero. La diferencial total se define entonces rigurosamente como

$${\displaystyle dy={\frac {\partial y}{\partial x_{1}}}\Delta x_{1}+\cdots +{\frac {\partial y}{\partial x_{n}}}\Delta x_{n}.}$$

Ya que con esta definición se tiene $${\displaystyle dx_{i}(\Delta x_{1},\dots ,\Delta x_{n})=\Delta x_{i},}$$ $${\displaystyle dy={\frac {\partial y}{\partial x_{1}}}\,dx_{1}+\cdots +{\frac {\partial y}{\partial x_{n}}}\,dx_{n}.}$$

Como en el caso de una variable, la identidad aproximada se cumple

$${\displaystyle dy\approx \Delta y}$$

en el que el error total puede hacerse tan pequeño como se desee limitando la atención a incrementos suficientemente pequeños. ${\textstyle {\sqrt {\Delta x_{1}^{2}+\cdots +\Delta x_{n}^{2}}}}$

Aplicación del diferencial total a la estimación del error

En medición, la diferencial total se utiliza para estimar el error de una función en función de los errores de los parámetros . Suponiendo que el intervalo es lo suficientemente corto para que el cambio sea aproximadamente lineal: ${\displaystyle \Delta f}$ ${\displaystyle f}$ ${\displaystyle \Delta x,\Delta y,\ldots }$ ${\displaystyle x,y,\ldots }$

$${\displaystyle \Delta f(x)=f'(x)\Delta x}$$

y que todas las variables son independientes, entonces para todas las variables,

$${\displaystyle \Delta f=f_{x}\Delta x+f_{y}\Delta y+\cdots }$$

Esto se debe a que la derivada con respecto al parámetro particular proporciona la sensibilidad de la función a un cambio en , en particular el error . Como se supone que son independientes, el análisis describe el escenario del peor caso. Se utilizan los valores absolutos de los errores de los componentes, porque después de un cálculo simple, la derivada puede tener un signo negativo. A partir de este principio se derivan las reglas de error de suma, multiplicación, etc., por ejemplo: ${\displaystyle f_{x}}$ ${\displaystyle x}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle \Delta x}$

Sea . Entonces, el error finito puede aproximarse como ${\displaystyle f(a,b)=ab}$

$${\displaystyle \Delta f=f_{a}\Delta a+f_{b}\Delta b.}$$Evaluación de las derivadas: Dividiendo por f , que es a × b $${\displaystyle \Delta f=b\Delta a+a\Delta b.}$$

$${\displaystyle {\frac {\Delta f}{f}}={\frac {\Delta a}{a}}+{\frac {\Delta b}{b}}}$$

Es decir, en la multiplicación, el error relativo total es la suma de los errores relativos de los parámetros.

Para ilustrar cómo esto depende de la función considerada, considere el caso donde la función es en cambio. Entonces, se puede calcular que la estimación del error es con un factor ' ln b ' adicional que no se encuentra en el caso de un producto simple. Este factor adicional tiende a hacer que el error sea menor, ya que ln b no es tan grande como un  b simple . ${\displaystyle f(a,b)=a\ln b}$ $${\displaystyle {\frac {\Delta f}{f}}={\frac {\Delta a}{a}}+{\frac {\Delta b}{b\ln b}}}$$

Diferenciales de orden superior

Las diferenciales de orden superior de una función y = f ( x ) de una sola variable x se pueden definir mediante: ^[8] y, en general, De manera informal, esto motiva la notación de Leibniz para derivadas de orden superior Cuando se permite que la variable independiente x dependa de otras variables, entonces la expresión se vuelve más complicada, ya que debe incluir también diferenciales de orden superior en la propia x . Así, por ejemplo, y así sucesivamente. $${\displaystyle d^{2}y=d(dy)=d(f'(x)dx)=(df'(x))dx=f''(x)\,(dx)^{2},}$$ $${\displaystyle d^{n}y=f^{(n)}(x)\,(dx)^{n}.}$$ $${\displaystyle f^{(n)}(x)={\frac {d^{n}f}{dx^{n}}}.}$$ $${\displaystyle {\begin{aligned}d^{2}y&=f''(x)\,(dx)^{2}+f'(x)d^{2}x\\[1ex]d^{3}y&=f'''(x)\,(dx)^{3}+3f''(x)dx\,d^{2}x+f'(x)d^{3}x\end{aligned}}}$$

Consideraciones similares se aplican a la definición de diferenciales de orden superior de funciones de varias variables. Por ejemplo, si f es una función de dos variables x e y , entonces donde es un coeficiente binomial . En más variables, se cumple una expresión análoga, pero con una expansión multinomial apropiada en lugar de una expansión binomial. ^[9] $${\displaystyle d^{n}f=\sum _{k=0}^{n}{\binom {n}{k}}{\frac {\partial ^{n}f}{\partial x^{k}\partial y^{n-k}}}(dx)^{k}(dy)^{n-k},}$$ ${\textstyle {\binom {n}{k}}}$

Las diferenciales de orden superior en varias variables también se vuelven más complicadas cuando se permite que las variables independientes dependan de otras variables. Por ejemplo, para una función f de x e y que se permite que dependan de variables auxiliares, se tiene $${\displaystyle d^{2}f=\left({\frac {\partial ^{2}f}{\partial x^{2}}}(dx)^{2}+2{\frac {\partial ^{2}f}{\partial x\partial y}}dx\,dy+{\frac {\partial ^{2}f}{\partial y^{2}}}(dy)^{2}\right)+{\frac {\partial f}{\partial x}}d^{2}x+{\frac {\partial f}{\partial y}}d^{2}y.}$$

Debido a esta incomodidad de notación, el uso de diferenciales de orden superior fue duramente criticado por Hadamard (1935), quien concluyó:

En fin, que significa o que representa la igualdad

$${\displaystyle d^{2}z=r\,dx^{2}+2s\,dx\,dy+t\,dy^{2}\,?}$$

A mi juicio, nada de todo.

Es decir: ¿qué se quiere decir, o qué se representa, finalmente, con la igualdad [...]? En mi opinión, nada en absoluto. A pesar de este escepticismo, las diferenciales de orden superior surgieron como una herramienta importante en el análisis. ^[10]

En estos contextos, la diferencial de orden n de la función f aplicada a un incremento Δ x se define mediante o una expresión equivalente, como donde es una diferencia hacia adelante de orden n con incremento t Δ x . $${\displaystyle d^{n}f(x,\Delta x)=\left.{\frac {d^{n}}{dt^{n}}}f(x+t\Delta x)\right|_{t=0}}$$ $${\displaystyle \lim _{t\to 0}{\frac {\Delta _{t\Delta x}^{n}f}{t^{n}}}}$$ ${\displaystyle \Delta _{t\Delta x}^{n}f}$

Esta definición también tiene sentido si f es una función de varias variables (para simplificar, se toma aquí como un argumento vectorial). Entonces, la n -ésima diferencial definida de esta manera es una función homogénea de grado n en el incremento vectorial Δ x . Además, la serie de Taylor de f en el punto x está dada por La derivada de Gateaux de orden superior generaliza estas consideraciones a espacios de dimensión infinita. $${\displaystyle f(x+\Delta x)\sim f(x)+df(x,\Delta x)+{\frac {1}{2}}d^{2}f(x,\Delta x)+\cdots +{\frac {1}{n!}}d^{n}f(x,\Delta x)+\cdots }$$

Propiedades

Varias propiedades de la diferencial se derivan de manera directa de las propiedades correspondientes de la derivada, la derivada parcial y la derivada total. Entre ellas se incluyen: ^[11]

• Linealidad : Para constantes a y b y funciones diferenciables f y g , $${\displaystyle d(af+bg)=a\,df+b\,dg.}$$
• Regla del producto : Para dos funciones diferenciables f y g , $${\displaystyle d(fg)=f\,dg+g\,df.}$$

Una operación d con estas dos propiedades se conoce en álgebra abstracta como derivación . Implican la regla de potencia Además, se cumplen varias formas de la regla de la cadena , con un nivel de generalidad creciente: ^[12] $${\displaystyle d(f^{n})=nf^{n-1}df}$$

• Si y = f ( u ) es una función diferenciable de la variable u y u = g ( x ) es una función diferenciable de x , entonces $${\displaystyle dy=f'(u)\,du=f'(g(x))g'(x)\,dx.}$$
• Si y = f ( x ₁ , ..., x _n ) y todas las variables  x ₁ , ..., x _n dependen de otra variable  t , entonces por la regla de la cadena para derivadas parciales , se tiene Heurísticamente, la regla de la cadena para varias variables puede entenderse dividiendo ambos lados de esta ecuación por la cantidad infinitamente pequeña dt . $${\displaystyle {\begin{aligned}dy={\frac {dy}{dt}}dt&={\frac {\partial y}{\partial x_{1}}}dx_{1}+\cdots +{\frac {\partial y}{\partial x_{n}}}dx_{n}\\[1ex]&={\frac {\partial y}{\partial x_{1}}}{\frac {dx_{1}}{dt}}\,dt+\cdots +{\frac {\partial y}{\partial x_{n}}}{\frac {dx_{n}}{dt}}\,dt.\end{aligned}}}$$
• Se cumplen expresiones análogas más generales, en las que las variables intermedias x _i dependen de más de una variable.

Formulación general

Se puede desarrollar una noción consistente de diferencial para una función f  : R ⁿ → R ^m entre dos espacios euclidianos . Sea x ,Δ x ∈ R ⁿ un par de vectores euclidianos . El incremento en la función f es Si existe una matriz A m × n tal que en la que el vector ε → 0 cuando Δ x → 0 , entonces f es por definición diferenciable en el punto x . La matriz A a veces se conoce como matriz jacobiana , y la transformación lineal que asocia al incremento Δ x ∈ R ⁿ del vector A Δ x ∈ R ^m se conoce, en este contexto general, como diferencial df ( x ) de f en el punto x . Esta es precisamente la derivada de Fréchet , y se puede hacer que la misma construcción funcione para una función entre cualesquiera espacios de Banach . $${\displaystyle \Delta f=f(\mathbf {x} +\Delta \mathbf {x} )-f(\mathbf {x} ).}$$ $${\displaystyle \Delta f=A\Delta \mathbf {x} +\|\Delta \mathbf {x} \|{\boldsymbol {\varepsilon }}}$$

Otro punto de vista fructífero es definir la diferencial directamente como una especie de derivada direccional : que es el enfoque ya adoptado para definir diferenciales de orden superior (y es el que más se aproxima a la definición establecida por Cauchy). Si t representa el tiempo y x la posición, entonces h representa una velocidad en lugar de un desplazamiento como lo hemos considerado hasta ahora. Esto produce otro refinamiento de la noción de diferencial: que debería ser una función lineal de una velocidad cinemática. El conjunto de todas las velocidades a través de un punto dado del espacio se conoce como el espacio tangente , y por lo tanto df da una función lineal en el espacio tangente: una forma diferencial . Con esta interpretación, la diferencial de f se conoce como la derivada exterior , y tiene una amplia aplicación en geometría diferencial porque la noción de velocidades y el espacio tangente tienen sentido en cualquier variedad diferenciable . Si, además, el valor de salida de f también representa una posición (en un espacio euclidiano), entonces un análisis dimensional confirma que el valor de salida de df debe ser una velocidad. Si uno trata el diferencial de esta manera, entonces se lo conoce como empuje hacia adelante ya que "empuja" las velocidades desde un espacio fuente hacia velocidades en un espacio destino. $${\displaystyle df(\mathbf {x} ,\mathbf {h} )=\lim _{t\to 0}{\frac {f(\mathbf {x} +t\mathbf {h} )-f(\mathbf {x} )}{t}}=\left.{\frac {d}{dt}}f(\mathbf {x} +t\mathbf {h} )\right|_{t=0},}$$

Otros enfoques

Aunque la noción de tener un incremento infinitesimal dx no está bien definida en el análisis matemático moderno , existe una variedad de técnicas para definir la diferencial infinitesimal de modo que la diferencial de una función pueda manejarse de una manera que no entre en conflicto con la notación de Leibniz . Estas incluyen:

• Definir la diferencial como una especie de forma diferencial , específicamente la derivada exterior de una función. Los incrementos infinitesimales se identifican entonces con vectores en el espacio tangente en un punto. Este enfoque es popular en geometría diferencial y campos relacionados, porque se generaliza fácilmente a aplicaciones entre variedades diferenciables .
• Diferenciales como elementos nilpotentes de anillos conmutativos . Este enfoque es popular en geometría algebraica . ^[13]
• Diferenciales en modelos suaves de teoría de conjuntos. Este enfoque se conoce como geometría diferencial sintética o análisis infinitesimal suave y está estrechamente relacionado con el enfoque geométrico algebraico, excepto que se utilizan ideas de la teoría de topos para ocultar los mecanismos por los cuales se introducen los infinitesimales nilpotentes. ^[14]
• Diferenciales como infinitesimales en sistemas de números hiperreales , que son extensiones de los números reales que contienen infinitesimales invertibles y números infinitamente grandes. Este es el enfoque del análisis no estándar iniciado por Abraham Robinson . ^[15]

Ejemplos y aplicaciones

Las diferenciales pueden usarse eficazmente en el análisis numérico para estudiar la propagación de errores experimentales en un cálculo y, por lo tanto, la estabilidad numérica general de un problema (Courant 1937a). Supongamos que la variable x representa el resultado de un experimento e y es el resultado de un cálculo numérico aplicado a x . La pregunta es hasta qué punto los errores en la medición de x influyen en el resultado del cálculo de y . Si x se conoce dentro de Δ x de su valor verdadero, entonces el teorema de Taylor da la siguiente estimación del error Δ y en el cálculo de y : donde ξ = x + θ Δ x para algún 0 < θ < 1 . Si Δ x es pequeño, entonces el término de segundo orden es despreciable, de modo que Δ y es, para fines prácticos, bien aproximado por dy = f' ( x ) Δ x . $${\displaystyle \Delta y=f'(x)\Delta x+{\frac {(\Delta x)^{2}}{2}}f''(\xi )}$$

La diferencial suele ser útil para reescribir una ecuación diferencial en la forma , en particular cuando se quieren separar las variables . $${\displaystyle {\frac {dy}{dx}}=g(x)}$$ $${\displaystyle dy=g(x)\,dx,}$$

Notas

1. Para una descripción histórica detallada de la diferencial, véase Boyer 1959, especialmente la página 275, donde se encuentra la contribución de Cauchy sobre el tema. Una descripción abreviada aparece en Kline 1972, capítulo 40.
2. Cauchy negó explícitamente la posibilidad de cantidades reales infinitesimales e infinitas (Boyer 1959, pp. 273-275), y adoptó el punto de vista radicalmente diferente de que "una cantidad variable se vuelve infinitamente pequeña cuando su valor numérico disminuye indefinidamente de tal manera que converge a cero" (Cauchy 1823, p. 12; traducción de Boyer 1959, p. 273).
3. Boyer 1959, pág. 275
4. Boyer 1959, p. 12: "Los diferenciales así definidos son sólo nuevas variables , y no infinitesimales fijos..."
5. Courant 1937a, II, §9: "Aquí observamos sólo de pasada que es posible utilizar esta representación aproximada del incremento por la expresión lineal para construir una definición lógicamente satisfactoria de un "diferencial", como lo hizo Cauchy en particular". ${\displaystyle \Delta y}$ ${\displaystyle hf(x)}$
6. Boyer 1959, pág. 284
7. Véanse, por ejemplo, los influyentes tratados de Courant 1937a, Kline 1977, Goursat 1904 y Hardy 1908. Las fuentes terciarias para esta definición incluyen también Tolstov 2001 e Itô 1993, §106.
8. Cauchy 1823. Véase también, por ejemplo, Goursat 1904, I, §14.
9. Goursat 1904, I, §14
10. En particular, a la holomorfía de dimensión infinita (Hille y Phillips 1974) y al análisis numérico a través del cálculo de diferencias finitas .
11. Goursat 1904, I, §17
12. Goursat 1904, I, §§14,16
13. Eisenbud y Harris 1998.
14. Véase Kock 2006 y Moerdijk & Reyes 1991.
15. Véase Robinson 1996 y Keisler 1986.

Véase también

• Notación para diferenciación

Referencias

• Boyer, Carl B. (1959), La historia del cálculo y su desarrollo conceptual , Nueva York: Dover Publications , MR  0124178.
• Cauchy, Augustin-Louis (1823), Résumé des Leçons données à l'Ecole royale polytechnique sur les apps du calcul infinitésimal, archivado desde el original el 2007-07-08 , consultado el 19 de agosto de 2009..
• Courant, Richard (1937a), Cálculo diferencial e integral. Vol. I , Wiley Classics Library, Nueva York: John Wiley & Sons (publicado en 1988), ISBN 978-0-471-60842-4, Sr.  1009558.
• Courant, Richard (1937b), Cálculo diferencial e integral. Vol. II , Wiley Classics Library, Nueva York: John Wiley & Sons (publicado en 1988), ISBN 978-0-471-60840-0, Sr.  1009559.
• Courant, Richard ; John, Fritz (1999), Introducción al cálculo y análisis Volumen 1 , Classics in Mathematics, Berlín, Nueva York: Springer-Verlag , ISBN 3-540-65058-X, Sr.  1746554
• Eisenbud, David ; Harris, Joe (1998), La geometría de los esquemas , Springer-Verlag, ISBN 0-387-98637-5.
• Fréchet, Maurice (1925), "La notion de différentielle dans l'analyse générale", Annales Scientifiques de l'École Normale Supérieure , Série 3, 42 : 293–323, doi : 10.24033/asens.766 , ISSN  0012-9593, Señor  1509268.
• Goursat, Édouard (1904), Un curso de análisis matemático: Vol 1: Derivadas y diferenciales, integrales definidas, desarrollo en serie, aplicaciones a la geometría, ER Hedrick, Nueva York: Dover Publications (publicado en 1959), MR  0106155.
• Hadamard, Jacques (1935), "La notion de différentiel dans l'enseignement", Gaceta Matemática , XIX (236): 341–342, doi :10.2307/3606323, JSTOR  3606323.
• Hardy, Godfrey Harold (1908), Un curso de matemáticas puras , Cambridge University Press , ISBN 978-0-521-09227-2.
• Hille, Einar ; Phillips, Ralph S. (1974), Análisis funcional y semigrupos , Providence, RI: American Mathematical Society , MR  0423094.
• Itô, Kiyosi (1993), Diccionario enciclopédico de matemáticas (2.ª ed.), MIT Press , ISBN 978-0-262-59020-4.
• Kline, Morris (1977), "Capítulo 13: Diferenciales y la ley de la media", Cálculo: un enfoque intuitivo y físico , John Wiley and Sons.
• Kline, Morris (1972), Pensamiento matemático desde la antigüedad hasta los tiempos modernos (3.ª ed.), Oxford University Press (publicado en 1990), ISBN 978-0-19-506136-9
• Keisler, H. Jerome (1986), Cálculo elemental: un enfoque infinitesimal (2.ª ed.).
• Kock, Anders (2006), Geometría diferencial sintética (PDF) (2.ª ed.), Cambridge University Press.
• Moerdijk, I .; Reyes, GE (1991), Modelos para análisis infinitamente suave , Springer-Verlag.
• Robinson, Abraham (1996), Análisis no estándar , Princeton University Press , ISBN 978-0-691-04490-3.
• Tolstov, GP (2001) [1994], "Diferencial", Enciclopedia de Matemáticas , EMS Press.

Enlaces externos

• Diferencial de una función en el proyecto de demostraciones Wolfram