Optimización por enjambre de partículas
PSO es una metaheurística, ya que asume pocas o ninguna hipótesis sobre el problema a optimizar y puede aplicarse en grandes espacios de soluciones candidatas.
Cada abeja vuela de modo errático por el espacio, recordando en todo momento cuál es la región donde ha visto más flores.
A su vez, el enjambre sabe colectivamente cuál es la región del espacio, de entre todas las exploradas, donde se han encontrado más flores.
Cada abeja variará individualmente su movimiento con arreglo a estas dos direcciones, volando hacia algún lugar intermedio.
Pasado un tiempo, si se descubre otra región con mayor densidad floral, el enjambre reorientará nuevamente la búsqueda hacia allí, y así sucesivamente.
Dichas partículas se desplazan a lo largo del espacio de búsqueda conforme unas simples reglas matemáticas.
El proceso se repite con el objetivo, no garantizado, de hallar en algún momento una solución lo suficientemente satisfactoria.
Lo descrito anteriormente puede formalizarse del siguiente modo: sea f: ℝn → ℝ la función de coste que se desea minimizar.
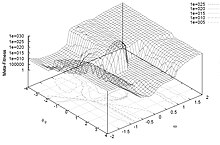
Para obtener soluciones con una hipersuperfie "poco irregular" en general se necesitan pocas partículas e iteraciones; en cambio, para conseguir soluciones de hipersuperficie "más irregular" se requiere una búsqueda más a fondo, que involucre mayor cantidad de partículas e iteraciones.
la búsqueda de los mejores pastos llevada a cabo por la ganadería trashumante, donde grandes rebaños han de atravesar terrenos difíciles y abruptos para alcanzar los mejores prados (léase óptimo global), mientras que rebaños más pequeños pueden bastarse con terrenos menos densos en vegetación (óptimo local), usando pocas iteraciones.
[21] La topología no es necesariamente fija, puede ser adaptativa según el caso (SPSO,[22] estrella estocástica,[23] TRIBES,[24] Cyber Swarm,[25] C-PSO[26]).
Esta interpretación ha dado pie a numerosas variantes dentro de la PSO, como se expone más adelante.
Este planteamiento ha llevado a simplificar los algoritmos de PSO, como se explica en un apartado posterior.
No obstante, estos análisis han sido objeto de críticas al ser considerados demasiado simplistas,[20] toda vez que asumen que el enjambre posee una sola partícula, sin variables aleatorias, y que la mejor posición p conocida de la partícula y la mejor posición global g del enjambre permanecen constantes durante el proceso de optimización.
Asimismo, ciertos análisis admiten un número infinito de iteraciones en la optimización, lo cual no es posible en un escenario real.
[29] Otra opción es modificar el propio algoritmo para hacerlo menos sensible al sistema de coordenadas.
Algunas de estas opciones y su impacto potencial en el rendimiento han sido discutidos en la literatura especializada.
[13][19][20][38] Con su puesta en práctica se han observado mejoras en el rendimiento, mayor facilidad para ajustar los parámetros y un comportamiento más consistente ante distintos problemas de optimización.
Como las ecuaciones usadas en PSO operan con números reales, un método común a la hora de resolver problemas discretos es mapear el espacio de búsqueda a un dominio continuo, para aplicar PSO clásica, y luego desmapear el resultado.