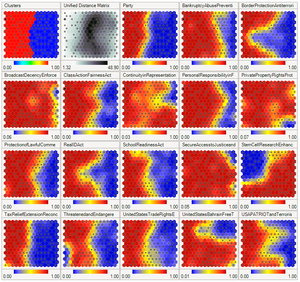
Mapa autoorganizado
El modelo fue descrito por primera vez como una red neuronal artificial por el profesor finlandés Teuvo Kohonen, debido a lo cual en ocasiones son llamadas redes o mapas de Kohonen.
[1][2] Al igual que la mayoría de las redes neuronales artificiales, los SOMs operan en dos modos: entrenamiento y mapeo.
Un mapa autoorganizado consiste en componentes llamadas nodos o neuronas.
Existen extensiones útiles que incluyen el uso de rejillas toroidales donde los ejes opuestos son conectados y usan un gran número de neuronas.
Se ha demostrado que mientras los SOMs con un pequeño número de neuronas tienen un comportamiento similar a las K-medias, los grandes mapas autoorganizados reconfiguran los datos de forma fundamentalmente topológica en carácter.
[4] Por ejemplo en una rejilla cuadrada se deben considerar cercanos 4 u 8 neuronas, según las vecindades de Von Neumann y Moore respectivamente.
[5] El objetivo del aprendizaje en los mapas autoorganizados es provocar que diferentes partes de la red respondan similarmente a ciertos patrones de la entrada.
Esto es parcialmente motivado por el manejo en partes separadas de la corteza cerebral del cerebro humano de la información sensorial, como la visual y la auditiva.
Con la segunda alternativa el aprendizaje es mucho más rápido puesto que los pesos iniciales ya dan una buena aproximación de los pesos reales.
[7] La red debe ser alimentada con un gran número de ejemplos entrenantes que representen, tan bien como sea posible, la naturaleza de los vectores esperados durante el mapeo.
Los ejemplos usualmente son administrados varias veces de forma iterativa.
Los pesos del BMU y las neuronas cercanas al mismo en la cuadrícula del SOM son ajustados hacia el vector de entrada.
La magnitud de los cambios se decrementan con el tiempo y con la distancia desde el BMU.
[6] Al inicio, cuando la vecindad es completa, la autoorganización tiene lugar a escala global.
explora rápidamente el conjunto de entrenamiento) el decrecimiento ocurre más lentamente.
Durante el mapeo, solo existirá una neurona ganadora, la neurona cuyo vector de pesos se encuentre más cerca del vector de entrada.
Mientras que la representación de los datos de entrada como vectores ha sido enfatizado en este artículo, se debe notar que cualquier clase de objeto puede ser representado digitalmente, definiendo una medida de distancia apropiada y las operaciones necesarias para que sea posible el entrenamiento usado para la construcción del mapa autoorganizado.
Esto incluye matrices, funciones continuas, e incluso otros mapas autoorganizados.
Debido a que en la fase de entrenamiento los pesos de toda la vecindad son movidos en la misma dirección, elementos similares tienden a excitar neuronas adyacentes.
Los mapas autoorganizados se consideran una generalización no linear del análisis de componentes principales (PCA por sus siglas en inglés).
[9] Esto ha sido mostrado usando datos geofísicos artificiales y reales, donde los SOMs ha tenido gran ventaja sobre los métodos convencionales de extracción de características como son las funciones ortogonales empíricas y el PCA.
Originalmente, los SOMs no fueron formulados como una solución a problemas de optimización.
No obstante, ha habido varios intentos por modificar la definición de los SOMs para dar solución a estos problemas con resultados similares.