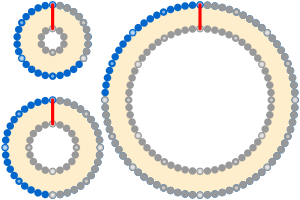
Cuerda que rodea la Tierra
El problema de la cuerda que rodea la Tierra es un acertijo matemático con una solución contraintuitiva.
Sorprendentemente, la respuesta correcta es que un gato pasará fácilmente por debajo de la cuerda, cuyo separación del suelo será de 1/2π metros o aproximadamente 16 cm.
Aún más sorprendente es que el tamaño de la esfera o círculo alrededor del cual se extiende la cuerda es irrelevante, y puede ser cualquier cosa desde el tamaño de un átomo hasta el de la Vía Láctea, y el resultado seguirá siendo 16 cm.
[1] Sea C la circunferencia de la Tierra, R su radio, c la longitud agregada a la cuerda y r el aumento del radio.
Como un círculo de radio R tiene una circunferencia de 2πR, entonces: independientemente del valor de C. Un corolario es que, para elevar la cuerda original 16 cm del suelo en todo el ecuador, solo se necesita agregar 1 m a la cuerda.