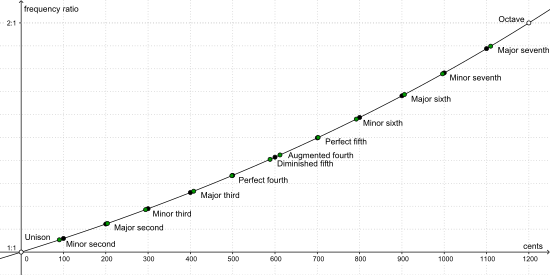
Cent

Equivale a una centésima de semitono temperado.

En cambio los intervalos físicos o puros tienen un número distinto.

Por ejemplo la quinta pura, perfecta o pitagórica, de razón 3:2, que tiene 702 cents).

El cent se utiliza como unidad de medida para cuantificar intervalos, y también para comparar intervalos semejantes en distintos sistemas de afinación.

= 1.00057778950655... que es la 1200ava parte geométrica o logarítmica de la octava.

Cuando se pretende hallar el número de cents de un intervalo cualquiera, el intervalo en cuestión es el dividendo, y el cent es el divisor.

Así pues, la medida en cents de un intervalo

Si se calcula previamente el logaritmo del divisor (que resulta en un número menor que la unidad), puede calcularse con buena aproximación multiplicando por el inverso del logaritmo.

Así, la medida aproximada en cents de un intervalo

El cent fue inventado en 1885 por el matemático y filólogo británico Alexander John Ellis (1814-1890).

La división decimal logarítmica del semitono ya había sido investigada por Gaspard de Prony (1755-1839) en los años 1830.

Ellis hizo innumerables medidas de instrumentos musicales de todo el mundo, utilizando los cents para informar y comparar las escalas empleadas.

y luego describió y empleó este sistema en su edición del libro On the Sensations of Tone de Hermann von Helmholtz (1821-1894)