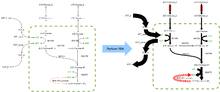
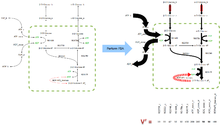
Análisis de balance de flujo
Estas tasas de crecimiento experimentales son comparadas con las predicciones del ABF, lo que permite corregir el modelo con las observaciones.
2001[1] (texto en inglés) el cual puede consultarse en el sitio web de Nature.
[2] Otros recursos son el libro "Systems Biology" de B. Palsson,[3] y artículos por J. Orth,[4] por Lee et al.
El único requisito para ser usada en ABF es que la red no contenga huecos.
Esto usualmente implica una curación manual, es decir, la revisión de artículos científicos por humanos para extraer las reacciones metabólicas reportadas en el sistema.
Algunos programas computacionales (Simpheny,[8][9] CellDesigner[10] y MetNetMaker[11]) aceleran la anotación de nuevas redes listas para su uso en ABF.
Generalmente los modelos son creados en formato BioPAX o SBML de modo que se pueda llevar a cabo un análisis o visualización más profundo; sin embargo estos formatos no son un requisito de ABF.
Esto le permite al modelo simular con mayor precisión el metabolismo real.
Los modelos metabólicos adaptados para ABF pueden ser analizados con COBRA toolbox[12] o FAME.
En ABF existe un gran número de soluciones matemáticamente aceptables para el problema del estado estacionario
Sin embargo algunas soluciones no tienen sentido biológico (no reflejan procesos que ocurran en la biología del sistema en la realidad), y las soluciones de interés son sólo aquellas que producen los metabolitos deseados en las proporciones correctas.
La función de biomasa juega un papel muy importante en hacer los resultados del ABF aplicables biológicamente (al asegurar que la proporción de metabolitos producida por el metabolismo sea la correcta, por ejemplo) por lo que debe ser definida con sensibilidad o medida experimentalmente.
Al modelar redes más pequeñas la función objetivo se modifica de acuerdo a estas.
Una red metabólica se compone de nodos (metabolitos) conectados por aristas con dirección (reacciones), por lo que puede representarse como una matriz.
Las propiedades de esta matriz son bien conocidas permitiendo analizar con computadoras problemas biológicos.
Existe un segundo obstáculo en la resolución del sistema: las tasas de reacción
Por ello el acercamiento de ecuaciones diferenciales sirve únicamente para modelar el metabolismo los organismos más estudiados (link to Heinemann E. Coli paper with all internal fluxes measured and Manchester yeast paper with internal fluxes measured).
(refiriéndose al número en relación con la estequiometría, S está comúnmente reservada para la entropía).
, es completamente equivalente a las ecuaciones derivadas directamente del diagrama de reacciones: Aplicando la condición homeostática: En general podemos escribir: con el
) y la mayoría de las reacciones son linearmente independientes existen muchos vectores
ABF tiene dos objetivos más: representar con precisión los límites del sistema y regresar la distribución de flujo más cercana a la que ocurre naturalmente dentro del sistema modelado.
), para asegurar que estos flujos conocidos sean reproducidos con precisión en la simulación.
La inhibición se simula restringiendo el flujo a través de una reacción.
El efecto puede clasificarse como letal o no letal aplicando el mismo criterio que con eliminación, definiendo un punto de corte para distinguir entre “reducción sustancial” y “reducción ligera”.
Con E. coli las tasas de crecimiento predichas en diferentes medios mantienen una correlación con los resultados experimentales.
A diferencia del Análisis del Punto de Asfixia, que sólo considera puntos en la red donde los metabolitos son producidos pero no consumidos y viceversa, ABF es una forma verdadera de modelaje de redes metabólicas puesto que sonsidera la red metabólica como una entidad completa en todas las etapas del análisis.
Esto implica que los efectos a nivel red, como reacciones químicas en vías distantes afectándose mutuamente, pueden ser reproducidos en el modelo.
La ventaja del Análisis del Punto de Asfixia consiste en que, por considerar cada reacción en aislamiento, puede sugerir cuáles son las reacciones importantes incluso si la red está altamente fragmentada y contiene huecos.
Es improbable que ABF pueda simular el funcionamiento de una célula nerviosa.
Debido a que la concentración interna de metabolitos no se considera en el modelo es posible que una solución de ABF contenga metabolitos a una concentración demasiado alta para ser biológicamente aceptable.