

La musicología clasifica comúnmente las escalas como hemitónicas o anhemitónicas . Las escalas hemitónicas contienen uno o más semitonos , mientras que las escalas anhemitónicas no contienen semitonos. Por ejemplo, en la música tradicional japonesa , la escala yo anhemitónica se contrasta con la escala in hemitónica . [4] La escala más simple y más utilizada en el mundo es la escala pentatónica "mayor" anhemitónica atritónica . La escala de tonos enteros también es anhemitónica.

Una subclase especial de las escalas hemitónicas son las escalas cohemitónicas . [6] Las escalas cohemitónicas contienen dos o más semitonos (lo que las convierte en hemitónicas) de modo que dos o más de los semitonos aparecen consecutivamente en el orden de la escala. Por ejemplo, la escala menor húngara en do incluye fa ♯ , sol y la ♭ en ese orden, con un semitono entre fa ♯ y sol, y luego un semitono entre sol y la ♭ .
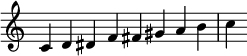

Las escalas ancohemitónicas , por el contrario, no contienen semitonos (y por lo tanto son anhemitónicas), o contienen semitonos (siendo hemitónicas) donde ninguno de los semitonos aparece consecutivamente en el orden de la escala. [7] [ verificación fallida ] Algunos autores, sin embargo, no incluyen escalas anhemitónicas en su definición de escalas ancohemitónicas. Los ejemplos de escalas ancohemitónicas son numerosos, ya que la ancohemitonia se favorece sobre la cohemitonia en las músicas del mundo: escala diatónica , mayor melódica / menor melódica , escala mayor armónica , escala menor armónica , escala mayor húngara , escala mayor rumana y la llamada escala octatónica .
La hemitonia también se cuantifica por el número de semitonos presentes. Las escalas no hemitónicas tienen solo un semitono; las escalas dihemitónicas tienen 2 semitonos; las escalas trihemitónicas tienen 3 semitonos, etc. De la misma manera que una escala anhemitónica es menos disonante que una escala hemitónica, una escala anhemitónica es menos disonante que una escala dihemitónica.
La calificación de cohemitónica versus ancohemitónica se combina con la cardinalidad de los semitonos, dando términos como: dicohemitónica, triancohemitónica, etc. Una escala ancohemitónica es menos disonante que una escala cohemitónica, siendo el conteo de sus semitonos igual. En general, el número de semitonos es más importante para la percepción de la disonancia que la adyacencia (o falta de ella) de cualquier par de ellos. La adyacencia adicional entre semitonos (una vez que la adyacencia está presente) no necesariamente aumenta la disonancia, siendo el conteo de semitonos nuevamente igual. [8]
Las escalas tritónicas y atritónicas están relacionadas con estas clasificaciones de semitonos . Las escalas tritónicas contienen uno o más tritonos , mientras que las escalas atritónicas no contienen tritonos. Existe una relación monótona especial entre los semitonos y los tritonos, ya que las escalas se construyen por proyección, como se ve a continuación.
La relación armónica de todas estas categorías proviene de la percepción de que los semitonos y tritonos son las disonancias más severas y que evitarlas es a menudo deseable. Las escalas más utilizadas en todo el planeta son anhemitónicas. De las escalas hemitónicas restantes, las más utilizadas son ancohemitónicas.
La mayor parte de la música del mundo es anhemitónica, quizás el 90%. [9] De esa otra porción hemitónica, quizás el 90% es no hemitónica, predominando en acordes de solo 1 semitono, todos los cuales son ancohemitónicos por definición. [9] Del 10% restante, quizás el 90% es dihemitónico, predominando en acordes de no más de 2 semitonos. Lo mismo se aplica a los acordes de 3 semitonos. [10] En ambos casos posteriores, sin embargo, hay una clara preferencia por la ancohemitónica, ya que la falta de adyacencia de dos semitonos contribuye en gran medida a suavizar la creciente disonancia.
La siguiente tabla representa gráficamente el tamaño de la sonoridad (hacia abajo a la izquierda) frente al número de semitonos (a la derecha) más la calidad de la ancohemitonia (indicada con la letra A) frente a la cohemitonia (indicada con la letra C). En general, las combinaciones ancohemitónicas son menos frecuentes para un acorde o tamaño de escala determinados, pero se utilizan con mucha más frecuencia, por lo que sus nombres son bien conocidos.
La columna "0" representa los acordes más utilizados, [8] evitando intervalos de M7 y novenas cromáticas y combinaciones de 4tas, 5tas cromáticas y 6tas para producir semitonos. La columna 1 representa acordes que apenas utilizan los grados armónicos que la columna "0" evita. La columna 2, sin embargo, representa sonidos mucho más intratables. [8]
La columna 0, fila 5 son los acordes completos pero agradables: 9.º, 6/9 y 9alt5 sin 7. [11] La columna "0", fila "6", es la única escala de tonos enteros . [12] [ verificación necesaria ] La columna "2A", fila "7", un mínimo local, se refiere a la escala diatónica y las escalas mayor melódica/ menor melódica . [13] [ verificación necesaria ] La ancohemitonia, entre otras cosas, probablemente hace que estas escalas sean populares. La columna "2C", fila "7", otro mínimo local, se refiere a la escala mayor napolitana , que es cohemitónica y algo menos común pero aún lo suficientemente popular como para llevar un nombre. [14] [ verificación necesaria ] La columna "3A", fila "7", otro mínimo local, representa la escala mayor armónica y su escala menor armónica de involución , y la escala mayor húngara y su escala mayor rumana de involución . [15] [ verificación necesaria ] La columna "3A", fila "6", son los análogos hexatónicos de estas cuatro escalas familiares, [16] [ verificación necesaria ] una de las cuales es la escala aumentada , [17] [ verificación necesaria ] y otra el análogo de la escala octatónica - que aparece, sola y solitaria, en la columna ">=4A". fila "8". [18] [ =4A fila 8. (enero de 2020)"> verificación necesaria ] La columna "2A", fila "4", otro mínimo, representa algunas combinaciones armónicas francamente disonantes, pero extrañamente resonantes : mM9 con ningún 5, 11 ♭ 9, dom13 ♭ 9 y M7 ♯ 11. [11]
Nótese también que en la fila de cardinalidad más alta de cada columna antes de que comiencen los ceros terminales, los conteos de sonoridad son pequeños, excepto en la fila "7" y las columnas "3" de todo tipo. Esta explosión de posibilidad hemitónica asociada con la cardinalidad de nota 7 (y superior) posiblemente marca el límite inferior para la entidad llamada "escala" (en contraste con "acorde").
Como se muestra en la tabla, la anhemitonia es una propiedad del dominio de los conjuntos de notas con cardinalidad 2 a 6, mientras que la ancohemitonia es una propiedad del dominio de los conjuntos de notas con cardinalidad 4 a 8 (3 a 8 para ancohemitonia impropia, incluida también la unhemitonia). Esto coloca a la anhemitonia generalmente en el rango de los "acordes" y a la ancohemitonia generalmente en el rango de las "escalas".
La interrelación de los semitonos, tritonos y el aumento del número de notas se puede demostrar tomando cinco tonos consecutivos del círculo de quintas ; [19] comenzando en C, estos son C, G, D, A y E. Al transponer los tonos para que encajen en una octava, se reorganizan en la escala pentatónica mayor : C, D, E, G, A. Esta escala es anhemitónica, no tiene semitonos; es atritónica, no tiene tritonos.
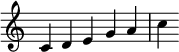
Además, este es el número máximo de notas tomadas consecutivamente del círculo de quintas para las cuales todavía es posible evitar un semitono. [20]
Si añadimos otra nota del círculo de quintas obtenemos la escala hexatónica mayor: CDEGA B. Esta escala es hemitónica, ya que tiene un semitono entre B y C; es atritónica, ya que no tiene tritonos. Además, este es el número máximo de notas tomadas consecutivamente del círculo de quintas para las que todavía es posible evitar un tritono. [21] [ verificación fallida ]
Si añadimos otra nota más del círculo de quintas obtenemos la escala heptatónica mayor: CDEFGAB (cuando la quinta se añade desde debajo de la tónica). Esta escala es estrictamente ancohemitónica, ya que tiene dos semitonos, pero no de forma consecutiva; es tritónica, ya que tiene un tritono entre F y B. Pasado este punto de la serie de proyecciones, no se añaden nuevos intervalos al análisis del vector de intervalos de la escala, [22] pero se produce la cohemitonia.

Si añadimos otra nota del círculo de quintas obtenemos la escala octatónica mayor: CDEFF ♯ GAB (cuando la quinta se añade desde encima de la nota superior de la serie, B en este caso). Esta escala es cohemitónica, ya que tiene 3 semitonos juntos en EFF ♯ G, y también tritónica. [22] [ verificación fallida ]
En general, se observa un comportamiento similar en todas las escalas: más notas en una escala tienden a agregar de manera acumulativa intervalos disonantes (específicamente: hemitonia y tritonia sin ningún orden en particular) y cohemitonia que no están ya presentes. Si bien también es cierto que más notas en una escala tienden a permitir más y más variados intervalos en el vector de intervalos , se podría decir que hay un punto de rendimientos decrecientes , cuando se compara con la disonancia también creciente, hemitonia, tritonia y cohemitonia. [22] Es cerca de estos puntos donde se encuentran las escalas más populares.
Aunque menos utilizadas que las escalas ancohemitónicas, las escalas cohemitónicas tienen una propiedad interesante. La secuencia de dos (o más) semitonos consecutivos en una escala presenta la oportunidad de "dividir" la escala colocando la nota tónica de la escala en la nota central del intervalo de semitonos. Esto permite que una nota principal desde abajo resuelva hacia arriba, así como una nota superior bemol-supertónica descendente , ambas convergiendo en la tónica. La división convierte una debilidad -disonancia de cohemitonia- en una fortaleza: convergencia contrapuntística en la tónica. Es muy común que una escala cohemitónica (o incluso hemitónica) (p. ej.: escala húngara menor { CDE ♭ F ♯ GA ♭ B }) se desplace preferentemente a un modo donde el intervalo de semitonos está dividido (p. ej.: escala armónica doble { GA ♭ BCDE ♭ F ♯ }), y por cuyo nombre conocemos más comúnmente la misma serie circular de intervalos. [23] Las escalas cohemitónicas con múltiples tramos de semitonos presentan la posibilidad adicional de modular entre tónicas, cada una provista de vecinos superiores e inferiores.

El sistema de tonalidades de la música occidental se basa en el supuesto de una escala heptatónica de 7 notas, de modo que nunca hay más de 7 alteraciones accidentales presentes en una tonalidad válida. La preferencia global por las escalas anhemitónicas se combina con esta base para destacar las 6 escalas heptatónicas ancohemitónicas, [24] [ verificación necesaria ] la mayoría de las cuales son comunes en la música romántica , y de las que se compone la mayor parte de la música romántica:
Estas escalas cohemitónicas son menos comunes:
Siguiendo la definición de escalas heptatónicas, todas ellas poseen 7 modos cada una y son adecuadas para su uso en mutación modal . [25] Aparecen en la tabla anterior en la fila "7", columnas "2A" y "3A".
A continuación se enumeran las armaduras de clave para todos los modos posibles no transpuestos de las escalas heptatónicas mencionadas anteriormente utilizando la nota C como tónica.