Solitón (óptica)

Término en óptica

En óptica , el término solitón se utiliza para referirse a cualquier campo óptico que no cambia durante la propagación debido a un delicado equilibrio entre los efectos no lineales y dispersivos en el medio. ^[1] Hay dos tipos principales de solitones:

• Solitones espaciales : el efecto no lineal puede equilibrar la dispersión . El campo electromagnético puede cambiar el índice de refracción del medio mientras se propaga, creando así una estructura similar a una fibra de índice graduado . ^[2] Si el campo es también un modo de propagación de la guía que ha creado, entonces permanecerá confinado y se propagará sin cambiar su forma.
• Solitones temporales : si el campo electromagnético ya está confinado espacialmente, es posible enviar pulsos que no cambiarán su forma porque los efectos no lineales equilibrarán la dispersión . Esos solitones se descubrieron primero y, a menudo, en óptica se les suele denominar simplemente "solitones".

solitones espaciales

cómo funciona una lente

Para poder entender cómo puede existir un solitón espacial, tenemos que hacer algunas consideraciones acerca de una lente convexa simple . Como se muestra en la imagen de la derecha, un campo óptico se acerca a la lente y luego se enfoca. El efecto de la lente es introducir un cambio de fase no uniforme que provoca el enfoque. Este cambio de fase es función del espacio y se puede representar con , cuya forma se representa aproximadamente en la imagen. ${\displaystyle \varphi (x)}$

El cambio de fase se puede expresar como el producto de la constante de fase y el ancho del camino que ha recorrido el campo. Podemos escribirlo como:

${\displaystyle \varphi (x)=k_{0}nL(x)}$

donde es el ancho de la lente, cambiando en cada punto con una forma que es la misma porque y n son constantes. En otras palabras, para conseguir un efecto de enfoque sólo tenemos que introducir un cambio de fase de dicha forma, pero no estamos obligados a cambiar el ancho. Si dejamos fijo el ancho L en cada punto, pero cambiamos el valor del índice de refracción conseguiremos exactamente el mismo efecto, pero con un enfoque completamente diferente. ${\displaystyle L(x)}$ ${\displaystyle \varphi (x)}$ ${\displaystyle k_{0}}$ ${\displaystyle n(x)}$

Esto tiene aplicación en fibras de índice graduado : el cambio en el índice de refracción introduce un efecto de enfoque que puede equilibrar la difracción natural del campo. Si los dos efectos se equilibran perfectamente, entonces tenemos un campo confinado que se propaga dentro de la fibra.

Los solitones espaciales se basan en el mismo principio: el efecto Kerr introduce una modulación de fase propia que cambia el índice de refracción según la intensidad:

${\displaystyle \varphi (x)=k_{0}n(x)L=k_{0}L[n+n_{2}I(x)]}$

Si tiene una forma similar a la que se muestra en la figura, entonces hemos creado el comportamiento de fase que queríamos y el campo mostrará un efecto de autoenfoque. En otras palabras, el campo crea una estructura guía similar a una fibra mientras se propaga. Si el campo crea una fibra y es el modo de dicha fibra al mismo tiempo, significa que los efectos no lineales de enfoque y lineales de difracción están perfectamente equilibrados y el campo se propagará para siempre sin cambiar su forma (siempre que el medio no no cambiar y si podemos descuidar las pérdidas, obviamente). Para que tenga un efecto de autoenfoque debemos tener un positivo , de lo contrario obtendremos el efecto contrario y no notaremos ningún comportamiento no lineal. ${\displaystyle I(x)}$ ${\displaystyle n_{2}}$

La guía de ondas óptica que crea el solitón mientras se propaga no es solo un modelo matemático, sino que en realidad existe y puede usarse para guiar otras ondas en diferentes frecuencias ^{[ cita requerida ]} . De esta manera es posible dejar que la luz interactúe con luz en diferentes frecuencias (esto es imposible en medios lineales).

Prueba

Un campo eléctrico se propaga en un medio que muestra el efecto óptico de Kerr , por lo que el índice de refracción viene dado por:

${\displaystyle n(I)=n+n_{2}I}$

Recordamos que la relación entre irradiancia y campo eléctrico es (en la representación compleja)

${\displaystyle I={\frac {|E|^{2}}{2\eta }}}$

donde y es la impedancia del espacio libre , dada por ${\displaystyle \eta =\eta _{0}/n}$ ${\displaystyle \eta _{0}}$

${\displaystyle \eta _{0}={\sqrt {\frac {\mu _{0}}{\varepsilon _{0}}}}\approx 377{\text{ }}\Omega .}$

El campo se propaga en la dirección con una constante de fase . Por ahora, ignoraremos cualquier dependencia del eje y , suponiendo que es infinito en esa dirección. Entonces el campo se puede expresar como: ${\displaystyle z}$ ${\displaystyle k_{0}n}$

${\displaystyle E(x,z,t)=A_{m}a(x,z)e^{i(k_{0}nz-\omega t)}}$

donde es la amplitud máxima del campo y es una función normalizada adimensional (de modo que su valor máximo es 1) que representa la forma del campo eléctrico entre el eje x . En general depende de z porque los campos cambian de forma mientras se propagan. Ahora tenemos que resolver la ecuación de Helmholtz : ${\displaystyle A_{m}}$ ${\displaystyle a(x,z)}$

${\displaystyle \nabla ^{2}E+k_{0}^{2}n^{2}(I)E=0}$

donde se señaló claramente que el índice de refracción (por lo tanto, la constante de fase) depende de la intensidad. Si reemplazamos la expresión del campo eléctrico en la ecuación, suponiendo que la envolvente cambia lentamente mientras se propaga, es decir ${\displaystyle a(x,z)}$

${\displaystyle \left|{\frac {\partial ^{2}a(x,z)}{\partial z^{2}}}\right|\ll \left|k_{0}{\frac {\partial a(x,z)}{\partial z}}\right|}$

la ecuación se convierte en:

${\displaystyle {\frac {\partial ^{2}a}{\partial x^{2}}}+i2k_{0}n{\frac {\partial a}{\partial z}}+k_{0}^{2}\left[n^{2}(I)-n^{2}\right]a=0.}$

Introduzcamos una aproximación que es válida porque los efectos no lineales son siempre mucho menores que los lineales:

${\displaystyle \left[n^{2}(I)-n^{2}\right]=[n(I)-n][n(I)+n]=n_{2}I(2n+n_{2}I)\approx 2nn_{2}I}$

ahora expresamos la intensidad en términos del campo eléctrico:

${\displaystyle \left[n^{2}(I)-n^{2}\right]\approx 2nn_{2}{\frac {|A_{m}|^{2}|a(x,z)|^{2}}{2\eta _{0}/n}}=n^{2}n_{2}{\frac {|A_{m}|^{2}|a(x,z)|^{2}}{\eta _{0}}}}$

la ecuación se convierte en:

${\displaystyle {\frac {1}{2k_{0}n}}{\frac {\partial ^{2}a}{\partial x^{2}}}+i{\frac {\partial a}{\partial z}}+{\frac {k_{0}nn_{2}|A_{m}|^{2}}{2\eta _{0}}}|a|^{2}a=0.}$

Ahora asumiremos que el efecto no lineal provocará el autoenfoque. Para que esto sea evidente, escribiremos en la ecuación. Ahora definamos algunos parámetros y reemplácelos en la ecuación: ${\displaystyle n_{2}>0}$ ${\displaystyle n_{2}=|n_{2}|}$

• ${\displaystyle \xi ={\frac {x}{X_{0}}}}$, entonces podemos expresar la dependencia del eje x con un parámetro adimensional; es una longitud, cuyo significado físico quedará más claro más adelante. ${\displaystyle X_{0}}$
• ${\displaystyle L_{d}=X_{0}^{2}k_{0}n}$, una vez que el campo eléctrico se ha propagado a través de z en esta longitud, ya no se pueden despreciar los efectos lineales de la difracción.
• ${\displaystyle \zeta ={\frac {z}{L_{d}}}}$, para estudiar la dependencia z con una variable adimensional.
• ${\displaystyle L_{n\ell }={\frac {2\eta _{0}}{k_{0}n|n_{2}|\cdot |A_{m}|^{2}}}}$, después de que el campo eléctrico se haya propagado a través de z durante esta longitud, los efectos no lineales ya no pueden despreciarse. Este parámetro depende de la intensidad del campo eléctrico, que es típico de los parámetros no lineales.
• ${\displaystyle N^{2}={\frac {L_{d}}{L_{n\ell }}}}$

La ecuación se convierte en:

${\displaystyle {\frac {1}{2}}{\frac {\partial ^{2}a}{\partial \xi ^{2}}}+i{\frac {\partial a}{\partial \zeta }}+N^{2}|a|^{2}a=0}$

esta es una ecuación común conocida como ecuación de Schrödinger no lineal . De esta forma, podemos entender el significado físico del parámetro N :

• si , entonces podemos ignorar la parte no lineal de la ecuación. Significa que el campo se verá afectado por el efecto lineal (difracción) mucho antes que el efecto no lineal, simplemente se difractará sin ningún comportamiento no lineal. ${\displaystyle N\ll 1}$ ${\displaystyle L_{d}\ll L_{n\ell }}$
• si , entonces el efecto no lineal será más evidente que la difracción y, debido a la automodulación de fase, el campo tenderá a enfocarse. ${\displaystyle N\gg 1}$
• si , entonces los dos efectos se equilibran y tenemos que resolver la ecuación. ${\displaystyle N\approx 1}$

Pues la solución de la ecuación es sencilla y es el solitón fundamental: ${\displaystyle N=1}$

${\displaystyle a(\xi ,\zeta )=\operatorname {sech} (\xi )e^{i\zeta /2}}$

donde sech es la secante hiperbólica . Todavía depende de z , pero sólo en fase, por lo que la forma del campo no cambiará durante la propagación.

Porque todavía es posible expresar la solución en forma cerrada, pero tiene una forma más complicada: ^[3] ${\displaystyle N=2}$

${\displaystyle a(\xi ,\zeta )={\frac {4[\cosh(3\xi )+3e^{4i\zeta }\cosh(\xi )]e^{i\zeta /2}}{\cosh(4\xi )+4\cosh(2\xi )+3\cos(4\zeta )}}.}$

Cambia su forma durante la propagación, pero es una función periódica de z con período . ${\displaystyle \zeta =\pi /2}$

Para soluciones de solitones, N debe ser un número entero y se dice que es el orden o el solitón. Para una solución exacta de forma cerrada también existe; ^[4] tiene una forma aún más complicada, pero ocurre la misma periodicidad. De hecho, todos los solitones tienen el punto . ^[5] Su forma sólo puede expresarse fácilmente inmediatamente después de la generación: ${\displaystyle N=3}$ ${\displaystyle N\geq 2}$ ${\displaystyle \zeta =\pi /2}$

${\displaystyle a(\xi ,\zeta =0)=N\operatorname {sech} (\xi )}$

a la derecha está la gráfica del solitón de segundo orden: al principio tiene forma de sech, luego aumenta la amplitud máxima y luego vuelve a la forma de sech. Dado que es necesaria una alta intensidad para generar solitones, si el campo aumenta aún más su intensidad el medio podría dañarse.

La condición a resolver si queremos generar un solitón fundamental se obtiene expresando N en términos de todos los parámetros conocidos y luego poniendo : ${\displaystyle N=1}$

${\displaystyle 1=N={\frac {L_{d}}{L_{n\ell }}}={\frac {X_{0}^{2}k_{0}^{2}n^{2}|n_{2}||A_{m}|^{2}}{2\eta _{0}}}}$

que, en términos de valor máximo de irradiancia, se convierte en:

${\displaystyle I_{\max }={\frac {|A_{m}|^{2}}{2\eta _{0}/n}}={\frac {1}{X_{0}^{2}k_{0}^{2}n|n_{2}|}}.}$

En la mayoría de los casos, las dos variables que se pueden cambiar son la intensidad máxima y el ancho del pulso . ${\displaystyle I_{\max }}$ ${\displaystyle X_{0}}$

Propagación de varios solitones ópticos de orden superior (serie de imágenes: baja potencia (sin solitón), luego n1 – n7)

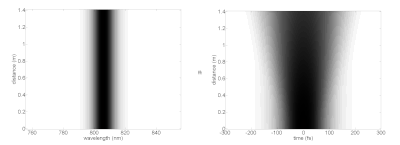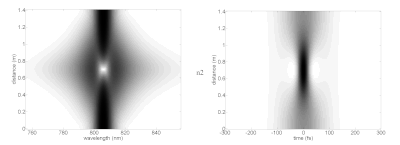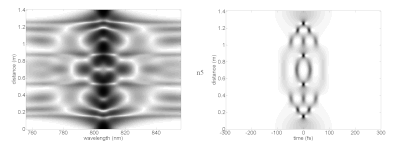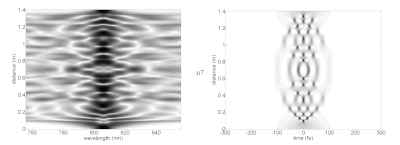
Curiosamente, los solitones de orden superior pueden adquirir formas complicadas antes de volver exactamente a su forma inicial al final del período del solitón. En la imagen de varios solitones, el espectro (izquierda) y el dominio del tiempo (derecha) se muestran a diferentes distancias de propagación (eje vertical) en un medio no lineal idealizado. Esto muestra cómo podría comportarse un pulso láser mientras viaja en un medio con las propiedades necesarias para soportar solitones fundamentales. En la práctica, para alcanzar la intensidad máxima muy alta necesaria para lograr efectos no lineales, los pulsos láser se pueden acoplar a fibras ópticas como la fibra de cristal fotónico con modos de propagación altamente confinados. Esas fibras tienen una dispersión más complicada y otras características que se apartan de los parámetros analíticos del solitón.

Generación de solitones espaciales.

El primer experimento con solitones ópticos espaciales fue realizado en 1974 por Ashkin y Bjorkholm ^[6] en una celda llena de vapor de sodio. Luego, el campo fue revisado en experimentos en la Universidad de Limoges ^[7] con disulfuro de carbono líquido y se expandió a principios de los años 90 con la primera observación de solitones en cristales fotorrefractivos, ^{[8] [9]} vidrio, semiconductores ^[10] y polímeros. Durante las últimas décadas se han reportado numerosos hallazgos en diversos materiales, para solitones de diferente dimensionalidad, forma, espirales, colisiones, fusiones, divisiones, en medios homogéneos, sistemas periódicos y guías de ondas. ^[11] Los solitones espaciales también se conocen como haces ópticos autoatrapados y su formación normalmente también va acompañada de una guía de ondas autoescrita. En los cristales líquidos nemáticos , ^[12] los solitones espaciales también se denominan nematicones .

Solitones de bloqueo de modo transversal

Pueden aparecer excitaciones localizadas en los láseres debido a la sincronización de los modos transversales.

Cavidad láser confocal con ganancia no lineal y cortes absorbentes en planos conjugados de Fourier ${\displaystyle 2F}$

En la cavidad del láser confocal, los modos transversales degenerados con un modo longitudinal único en la longitud de onda mezclados en un disco de ganancia no lineal (ubicado en ) y un disco absorbente saturable (ubicado en ) de diámetro son capaces de producir solitones espaciales de forma hiperbólica : ^[13] ${\displaystyle 2F}$ ${\displaystyle \lambda }$ ${\displaystyle G}$ ${\displaystyle z=0}$ ${\displaystyle \alpha }$ ${\displaystyle z=2F}$ ${\displaystyle D}$ ${\displaystyle \operatorname {sech} }$

${\displaystyle {\begin{aligned}E(x,z=0)&\sim \operatorname {sech} \left(\!{\frac {\pi xD}{2\lambda F}}{\sqrt {\frac {1-\alpha G}{G}}}\,\right)\\[3pt]E(x,z=2F)&\sim \operatorname {sech} \left(\!{\frac {2\pi x}{D}}{\sqrt {\frac {G}{1-\alpha G}}}\,\right)\end{aligned}}}$

en planos conjugados de Fourier y . ^[14] ${\displaystyle z=0}$ ${\displaystyle z=2F}$

solitones temporales

El principal problema que limita la velocidad de transmisión en fibras ópticas es la dispersión de velocidades de grupo . Esto se debe a que los impulsos generados tienen un ancho de banda distinto de cero y el medio por el que se propagan tiene un índice de refracción que depende de la frecuencia (o longitud de onda ). Este efecto está representado por el parámetro de dispersión de retardo de grupo D ; usándolo, es posible calcular exactamente cuánto se ampliará el pulso:

${\displaystyle \Delta \tau \approx DL\,\Delta \lambda }$

donde L es la longitud de la fibra y es el ancho de banda en términos de longitud de onda. El enfoque en los sistemas de comunicación modernos es equilibrar dicha dispersión con otras fibras que tienen D con diferentes signos en diferentes partes de la fibra: de esta manera los pulsos siguen ampliándose y encogiéndose mientras se propagan. Con los solitones temporales es posible eliminar este problema por completo. ${\displaystyle \Delta \lambda }$

Efectos lineales y no lineales sobre pulsos gaussianos.

Considere la imagen de la derecha. A la izquierda hay un pulso gaussiano estándar , es decir, la envolvente del campo que oscila a una frecuencia definida. Suponemos que la frecuencia permanece perfectamente constante durante el pulso.

Ahora dejamos que este pulso se propague a través de una fibra con , se verá afectado por la dispersión de velocidad del grupo. Para este signo de D , la dispersión es anómala , de modo que las componentes de mayor frecuencia se propagarán un poco más rápido que las de menor frecuencia, llegando así antes al final de la fibra. La señal general que recibimos es un pulso chirriante más amplio, que se muestra en la parte superior derecha de la imagen. ${\displaystyle D>0}$

efecto de la modulación de fase propia en la frecuencia

Ahora supongamos que tenemos un medio que muestra sólo el efecto Kerr no lineal pero su índice de refracción no depende de la frecuencia: tal medio no existe, pero vale la pena considerarlo para comprender los diferentes efectos.

La fase del campo viene dada por:

${\displaystyle \varphi (t)=\omega _{0}t-kz=\omega _{0}t-k_{0}z[n+n_{2}I(t)]}$

la frecuencia (según su definición) viene dada por:

${\displaystyle \omega (t)={\frac {\partial \varphi (t)}{\partial t}}=\omega _{0}-k_{0}zn_{2}{\frac {\partial I(t)}{\partial t}}}$

Esta situación está representada en la imagen de la izquierda. Al principio del pulso la frecuencia es menor, al final es mayor. Después de la propagación a través de nuestro medio ideal, obtendremos un pulso chirriante sin ampliación porque hemos descuidado la dispersión.

Volviendo a la primera imagen, vemos que los dos efectos introducen un cambio de frecuencia en dos direcciones opuestas diferentes. Es posible crear un pulso para que los dos efectos se equilibren entre sí. Considerando frecuencias más altas, la dispersión lineal tenderá a permitir que se propaguen más rápido, mientras que el efecto Kerr no lineal las ralentizará. El efecto general será que el pulso no cambia durante la propagación: tales pulsos se denominan solitones temporales.

Historia de los solitones temporales.

En 1973, Akira Hasegawa y Fred Tappert de AT&T Bell Labs fueron los primeros en sugerir que podrían existir solitones en las fibras ópticas , debido a un equilibrio entre la modulación de autofase y la dispersión anómala . ^{[15] [16]} También en 1973 Robin Bullough hizo el primer informe matemático sobre la existencia de solitones ópticos. También propuso la idea de un sistema de transmisión basado en solitones para aumentar el rendimiento de las telecomunicaciones ópticas .

Los solitones en un sistema de fibra óptica se describen mediante las ecuaciones de Manakov .

En 1987, P. Emplit, JP Hamaide, F. Reynaud, C. Froehly y A. Barthelemy, de las Universidades de Bruselas y Limoges, realizaron la primera observación experimental de la propagación de un solitón oscuro , en una fibra óptica.

En 1988, Linn Mollenauer y su equipo transmitieron pulsos de solitón a más de 4.000 kilómetros utilizando un fenómeno llamado efecto Raman , llamado así por el científico indio Sir CV Raman , quien lo describió por primera vez en la década de 1920, para proporcionar ganancia óptica en la fibra.

En 1991, un equipo de investigación de los Laboratorios Bell transmitió solitones sin errores a 2,5 gigabits a lo largo de más de 14.000 kilómetros, utilizando amplificadores de fibra óptica de erbio (segmentos empalmados de fibra óptica que contienen el elemento de tierras raras erbio). Los láseres de bomba, acoplados a los amplificadores ópticos, activan el erbio, que energiza los pulsos de luz ^{[ cita necesaria ]} .

En 1998, Thierry Georges y su equipo del Centro de I+D de France Télécom , combinando solitones ópticos de diferentes longitudes de onda ( multiplexación por división de longitud de onda ), demostraron una transmisión de datos de 1 terabit por segundo (1.000.000.000.000 de unidades de información por segundo) ^{[ cita necesaria ]} .

En 2020, Optics Communications informó a un equipo japonés de MEXT, conmutación de circuitos ópticos con ancho de banda de hasta 90 Tbps (terabits por segundo), Optics Communications, Volumen 466, 1 de julio de 2020, 125677.

Prueba de solitones temporales

Un campo eléctrico se propaga en un medio que muestra el efecto óptico de Kerr a través de una estructura guía (como una fibra óptica ) que limita la potencia en el plano xy . Si el campo se propaga hacia z con una constante de fase , entonces se puede expresar de la siguiente forma: ${\displaystyle \beta _{0}}$

${\displaystyle E(\mathbf {r} ,t)=A_{m}a(t,z)f(x,y)e^{i(\beta _{0}z-\omega _{0}t)}}$

donde es la amplitud máxima del campo, es la envolvente que da forma al impulso en el dominio del tiempo; en general depende de z porque el impulso puede cambiar de forma mientras se propaga; representa la forma del campo en el plano xy y no cambia durante la propagación porque hemos asumido que el campo es guiado. Tanto a como f son funciones adimensionales normalizadas cuyo valor máximo es 1, por lo que realmente representa la amplitud del campo. ${\displaystyle A_{m}}$ ${\displaystyle a(t,z)}$ ${\displaystyle f(x,y)}$ ${\displaystyle A_{m}}$

Dado que en el medio existe una dispersión que no podemos descuidar, la relación entre el campo eléctrico y su polarización viene dada por una integral de convolución . De todos modos, usando una representación en el dominio de Fourier , podemos reemplazar la convolución con un producto simple, usando así relaciones estándar que son válidas en medios más simples. Transformamos el campo eléctrico en Fourier usando la siguiente definición:

${\displaystyle {\tilde {E}}(\mathbf {r} ,\omega -\omega _{0})=\int \limits _{-\infty }^{\infty }E(\mathbf {r} ,t)e^{-i(\omega -\omega _{0})t}\,dt}$

Usando esta definición, una derivada en el dominio del tiempo corresponde a un producto en el dominio de Fourier:

${\displaystyle {\frac {\partial }{\partial t}}E\Longleftrightarrow i(\omega -\omega _{0}){\tilde {E}}}$

la expresión completa del campo en el dominio de la frecuencia es:

${\displaystyle {\tilde {E}}(\mathbf {r} ,\omega -\omega _{0})=A_{m}{\tilde {a}}(\omega ,z)f(x,y)e^{i\beta _{0}z}}$

Ahora podemos resolver la ecuación de Helmholtz en el dominio de la frecuencia:

${\displaystyle \nabla ^{2}{\tilde {E}}+n^{2}(\omega )k_{0}^{2}{\tilde {E}}=0}$

decidimos expresar la constante de fase con la siguiente notación:

${\displaystyle {\begin{aligned}n(\omega )k_{0}=\beta (\omega )&=\overbrace {\beta _{0}} ^{\text{linear non-dispersive}}+\overbrace {\beta _{\ell }(\omega )} ^{\text{linear dispersive}}+\overbrace {\beta _{n\ell }} ^{\text{non-linear}}\\[8pt]&=\beta _{0}+\Delta \beta (\omega )\end{aligned}}}$

donde asumimos que (la suma del componente dispersivo lineal y la parte no lineal) es una pequeña perturbación, es decir . La constante de fase puede tener cualquier comportamiento complicado, pero podemos representarla con una serie de Taylor centrada en : ${\displaystyle \Delta \beta }$ ${\displaystyle |\beta _{0}|\gg |\Delta \beta (\omega )|}$ ${\displaystyle \omega _{0}}$

${\displaystyle \beta (\omega )\approx \beta _{0}+(\omega -\omega _{0})\beta _{1}+{\frac {(\omega -\omega _{0})^{2}}{2}}\beta _{2}+\beta _{n\ell }}$

donde, como se sabe:

${\displaystyle \beta _{u}=\left.{\frac {d^{u}\beta (\omega )}{d\omega ^{u}}}\right|_{\omega =\omega _{0}}}$

Ponemos la expresión del campo eléctrico en la ecuación y hacemos algunos cálculos. Si asumimos la aproximación de la envolvente que varía lentamente :

${\displaystyle \left|{\frac {\partial ^{2}{\tilde {a}}}{\partial z^{2}}}\right|\ll \left|\beta _{0}{\frac {\partial {\tilde {a}}}{\partial z}}\right|}$

obtenemos:

${\displaystyle 2i\beta _{0}{\frac {\partial {\tilde {a}}}{\partial z}}+[\beta ^{2}(\omega )-\beta _{0}^{2}]{\tilde {a}}=0}$

estamos ignorando el comportamiento en el plano xy , porque ya se conoce y está dado por . Hacemos una pequeña aproximación, como hicimos para el solitón espacial: ${\displaystyle f(x,y)}$

${\displaystyle {\begin{aligned}\beta ^{2}(\omega )-\beta _{0}^{2}&=[\beta (\omega )-\beta _{0}][\beta (\omega )+\beta _{0}]\\[6pt]&=[\beta _{0}+\Delta \beta (\omega )-\beta _{0}][2\beta _{0}+\Delta \beta (\omega )]\approx 2\beta _{0}\,\Delta \beta (\omega )\end{aligned}}}$

reemplazando esto en la ecuación obtenemos simplemente:

${\displaystyle i{\frac {\partial {\tilde {a}}}{\partial z}}+\Delta \beta (\omega ){\tilde {a}}=0}$.

Ahora queremos volver al dominio del tiempo. Expresando los productos por derivadas obtenemos la dualidad:

${\displaystyle \Delta \beta (\omega )\Longleftrightarrow i\beta _{1}{\frac {\partial }{\partial t}}-{\frac {\beta _{2}}{2}}{\frac {\partial ^{2}}{\partial t^{2}}}+\beta _{n\ell }}$

Podemos escribir la componente no lineal en términos de irradiancia o amplitud del campo:

${\displaystyle \beta _{n\ell }=k_{0}n_{2}I=k_{0}n_{2}{\frac {|E|^{2}}{2\eta _{0}/n}}=k_{0}n_{2}n{\frac {|A_{m}|^{2}}{2\eta _{0}}}|a|^{2}}$

para la dualidad con el solitón espacial, definimos:

${\displaystyle L_{n\ell }={\frac {2\eta _{0}}{k_{0}nn_{2}|A_{m}|^{2}}}}$

y este símbolo tiene el mismo significado que el caso anterior, aunque el contexto sea diferente. La ecuación se convierte en:

${\displaystyle i{\frac {\partial a}{\partial z}}+i\beta _{1}{\frac {\partial a}{\partial t}}-{\frac {\beta _{2}}{2}}{\frac {\partial ^{2}a}{\partial t^{2}}}+{\frac {1}{L_{n\ell }}}|a|^{2}a=0}$

Sabemos que el impulso se propaga a lo largo del eje z con una velocidad de grupo dada por , por lo que no nos interesa porque solo queremos saber cómo el pulso cambia su forma mientras se propaga. Decidimos estudiar la forma del impulso, es decir, la función envolvente a (·) utilizando una referencia que se mueve con el campo a la misma velocidad. Así hacemos la sustitución ${\displaystyle v_{g}=1/\beta _{1}}$

${\displaystyle T=t-\beta _{1}z}$

y la ecuación queda:

${\displaystyle i{\frac {\partial a}{\partial z}}-{\frac {\beta _{2}}{2}}{\frac {\partial ^{2}a}{\partial T^{2}}}+{\frac {1}{L_{n\ell }}}|a|^{2}a=0}$

Ahora asumimos además que el medio donde se propaga el campo muestra una dispersión anómala , es decir , en términos del parámetro de dispersión del retardo de grupo . Hacemos esto más evidente reemplazando en la ecuación . Definamos ahora los siguientes parámetros (la dualidad con el caso anterior es evidente): ${\displaystyle \beta _{2}<0}$ ${\displaystyle D={\frac {-2\pi c}{\lambda ^{2}}}\beta _{2}>0}$ ${\displaystyle \beta _{2}=-|\beta _{2}|}$

${\displaystyle L_{d}={\frac {T_{0}^{2}}{|\beta _{2}|}};\qquad \tau ={\frac {T}{T_{0}}};\qquad \zeta ={\frac {z}{L_{d}}};\qquad N^{2}={\frac {L_{d}}{L_{n\ell }}}}$

reemplazando los de la ecuación obtenemos:

${\displaystyle {\frac {1}{2}}{\frac {\partial ^{2}a}{\partial \tau ^{2}}}+i{\frac {\partial a}{\partial \zeta }}+N^{2}|a|^{2}a=0}$

esa es exactamente la misma ecuación que hemos obtenido en el caso anterior. El solitón de primer orden viene dado por:

${\displaystyle a(\tau ,\zeta )=\operatorname {sech} (\tau )e^{i\zeta /2}}$

Las mismas consideraciones que hemos hecho son válidas en este caso. La condición N  = 1 se convierte en una condición sobre la amplitud del campo eléctrico:

${\displaystyle |A_{m}|^{2}={\frac {2\eta _{0}|\beta _{2}|}{T_{0}^{2}n_{2}k_{0}n}}}$

o, en términos de irradiancia:

${\displaystyle I_{\max }={\frac {|A_{m}|^{2}}{2\eta _{0}/n}}={\frac {|\beta _{2}|}{T_{0}^{2}n_{2}k_{0}}}}$

o podemos expresarlo en términos de potencia si introducimos un área efectiva definida de modo que : ${\displaystyle A_{\text{eff}}}$ ${\displaystyle P=IA_{\text{eff}}}$

${\displaystyle P={\frac {|\beta _{2}|A_{\text{eff}}}{T_{0}^{2}n_{2}k_{0}}}}$

Estabilidad de los solitones

Hemos descrito qué son los solitones ópticos y, usando las matemáticas, hemos visto que, si queremos crearlos, tenemos que crear un campo con una forma particular (sólo para el primer orden) con una potencia particular relacionada con la duración. del impulso. Pero ¿qué pasa si nos equivocamos un poco al crear tales impulsos? Agregando pequeñas perturbaciones a las ecuaciones y resolviéndolas numéricamente, es posible demostrar que los solitones monodimensionales son estables. A menudo se les conoce como (1 + 1) D solitones , lo que significa que están limitados en una dimensión ( x o t , como hemos visto) y se propagan en otra ( z ).

Si creamos un solitón de este tipo usando una potencia o forma ligeramente incorrecta, entonces se ajustará hasta alcanzar la forma estándar de sech con la potencia correcta. Desafortunadamente esto se logra a expensas de cierta pérdida de energía, que puede causar problemas porque puede generar otro campo no solitón que se propaga junto con el campo que queremos. Los solitones monodimensionales son muy estables: por ejemplo, si de todos modos generamos un solitón de primer orden; si N es mayor, generaremos un solitón de orden superior, pero el enfoque que realiza durante la propagación puede provocar picos de potencia elevados que dañen los medios. ${\displaystyle 0.5<N<1.5}$

La única forma de crear un solitón espacial (1 + 1) D es limitar el campo en el eje y usando una losa dieléctrica y luego limitar el campo en x usando el solitón.

Por otro lado, los solitones espaciales (2 + 1) D son inestables, por lo que cualquier pequeña perturbación (debida al ruido, por ejemplo) puede hacer que el solitón se difracte como un campo en un medio lineal o colapse, dañando así el material. Es posible crear solitones espaciales estables (2 + 1) D utilizando medios no lineales saturados, donde la relación de Kerr es válida hasta que alcanza un valor máximo. Trabajar cerca de este nivel de saturación permite crear un solitón estable en un espacio tridimensional. ${\displaystyle n(I)=n+n_{2}I}$

Si consideramos la propagación de pulsos de luz más cortos (temporales) o a mayor distancia, necesitamos considerar correcciones de orden superior y, por lo tanto, la envolvente de la portadora del pulso se rige por la ecuación de Schrödinger no lineal de orden superior (HONSE), para la cual existen algunas Soluciones de solitones especializadas (analíticas). ^[17]

Efecto de las pérdidas de energía.

Como hemos visto, para poder crear un solitón es necesario tener la potencia adecuada a la hora de generarlo. Si no hay pérdidas en el medio, entonces sabemos que el solitón seguirá propagándose para siempre sin cambiar de forma (primer orden) o cambiar su forma periódicamente (órdenes superiores). Lamentablemente cualquier medio introduce pérdidas, por lo que el comportamiento real de la potencia será de la forma:

${\displaystyle P(z)=P_{0}e^{-\alpha z}}$

Este es un problema grave para los solitones temporales que se propagan en fibras a lo largo de varios kilómetros. Consideremos lo que sucede con los solitones temporales, la generalización a los espaciales es inmediata. Hemos demostrado que la relación entre potencia y duración del impulso es: ${\displaystyle P_{0}}$ ${\displaystyle T_{0}}$

${\displaystyle P={\frac {|\beta _{2}|A_{\text{eff}}}{T_{0}^{2}n_{2}k_{0}}}}$

si el poder cambia, lo único que puede cambiar en la segunda parte de la relación es . si sumamos pérdidas a la potencia y resolvemos la relación en términos de obtenemos: ${\displaystyle T_{0}}$ ${\displaystyle T_{0}}$

${\displaystyle T(z)=T_{0}e^{(\alpha /2)z}}$

¡La amplitud del impulso crece exponencialmente para equilibrar las pérdidas! esta relación es cierta mientras exista el solitón, es decir, hasta que esta perturbación sea pequeña, por lo que debe ser así, de lo contrario no podemos usar las ecuaciones para solitones y tenemos que estudiar la dispersión lineal estándar. Si queremos crear un sistema de transmisión utilizando fibras ópticas y solitones, tenemos que añadir amplificadores ópticos para limitar la pérdida de potencia. ${\displaystyle \alpha z\ll 1}$

Generación de pulso de solitón.

Se han llevado a cabo experimentos para analizar el efecto del efecto Kerr no lineal inducido por un campo magnético externo de alta frecuencia (20 MHz-1 GHz) en fibras ópticas monomodo de longitud considerable (50-100 m) para compensar la dispersión de velocidad de grupo (GVD) y la posterior. Evolución del pulso de solitón (energía máxima, pulso hiperbólico secante, estrecho). ^[18] La generación de pulso de solitón en fibra es una conclusión obvia como modulación de fase propia debido a la alta energía del pulso compensado GVD, mientras que la longitud de evolución es de 2000 km. (la longitud de onda del láser elegida es superior a 1,3 micrómetros). Además, el pulso máximo de solitón tiene un período de 1 a 3 ps para que se acomode de manera segura en el ancho de banda óptico. Una vez que se genera el pulso de solitón, se dispersa menos en miles de kilómetros de longitud de fibra, lo que limita el número de estaciones repetidoras.

solitones oscuros

En el análisis de ambos tipos de solitones hemos asumido condiciones particulares sobre el medio:

• en solitones espaciales, eso significa que la modulación de fase propia provoca el autoenfoque ${\displaystyle n_{2}>0}$
• en solitones temporales, o dispersión anómala ${\displaystyle \beta _{2}<0}$ ${\displaystyle D>0}$

¿Es posible obtener solitones si no se verifican esas condiciones? si asumimos o , obtenemos la siguiente ecuación diferencial (tiene la misma forma en ambos casos, usaremos sólo la notación del solitón temporal): ${\displaystyle n_{2}<0}$ ${\displaystyle \beta _{2}>0}$

${\displaystyle {\frac {-1}{2}}{\frac {\partial ^{2}a}{\partial \tau ^{2}}}+i{\frac {\partial a}{\partial \zeta }}+N^{2}|a|^{2}a=0.}$

Esta ecuación tiene soluciones similares a las de un solitón. Para el primer orden ( N  = 1):

${\displaystyle a(\tau ,\zeta )=\tanh(\tau )e^{i\zeta }.\ }$

poder de un solitón oscuro

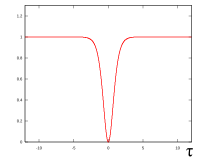
La trama de se muestra en la imagen de la derecha. Para solitones de orden superior ( ) podemos utilizar la siguiente expresión en forma cerrada: ${\displaystyle |a(\tau ,\zeta )|^{2}}$ ${\displaystyle N>1}$

${\displaystyle a(\tau ,\zeta =0)=N\tanh(\tau ).\ }$

Es un solitón, en el sentido de que se propaga sin cambiar de forma, pero no está formado por un pulso normal; más bien, es una falta de energía en un haz de tiempo continuo. La intensidad es constante, pero durante un breve periodo de tiempo durante el cual salta a cero y regresa, generando así un "pulso oscuro". En realidad, esos solitones se pueden generar introduciendo pulsos cortos y oscuros en pulsos estándar mucho más largos. Los solitones oscuros son más difíciles de manejar que los solitones estándar, pero han demostrado ser más estables y resistentes a las pérdidas.

Ver también

• solitón
• Modulación de fase propia
• Efecto Kerr óptico
• solitón vectorial
• nematicón
• Pulso ultracorto

Referencias

1. Taylor, James Roy (1992). Solitones ópticos: teoría y experimento . Cambridge: Prensa de la Universidad de Cambridge . ISBN 9780521405485. OCLC  23975147.
2. Rashidian Vaziri, señor (2013). "Descripción de la propagación de intensos pulsos láser en medios Kerr no lineales utilizando el modelo de conductos". Física del Láser . 23 (10): 105401. Código bibliográfico : 2013LaPhy..23j5401R. doi :10.1088/1054-660X/23/10/105401. S2CID  250912159.
3. Chen, Chin-Lin (11 de septiembre de 2006). Fundamentos de la óptica de ondas guiadas. John Wiley e hijos. ISBN 9780470042212.
4. Chen, Chin-Lin (11 de septiembre de 2006). Fundamentos de la óptica de ondas guiadas. John Wiley e hijos. ISBN 9780470042212.
5. Agrawal, Govind P. (2007). Fibra Óptica No Lineal. Prensa académica. ISBN 9780123695161.
6. JE Bjorkholm; A. Ashkin (1974). "cw autoenfoque y autoatrapamiento de luz en vapor de sodio". Física. Rev. Lett . 32 (4): 129. Código bibliográfico : 1974PhRvL..32..129B. doi :10.1103/PhysRevLett.32.129.
7. A. Barthelemy, S. Maneuf y C. Froehly (1985). "Propagación de solitón y autoconfinamiento de faisceaux láser por no linealidad óptica de kerr". Optar. Comunitario . 55 (3): 201. Código Bib :1985OptCo..55..201B. doi :10.1016/0030-4018(85)90047-1.
8. M. Segev; et al. (1992). "Solitones espaciales en medios fotorrefractivos". Física. Rev. Lett . 68 (7): 923–926. Código bibliográfico : 1992PhRvL..68..923S. doi : 10.1103/PhysRevLett.68.923. PMID  10046033.
9. E. DelRe y M. Segev (2009). "Autoenfoque y solitones en medios fotorrefractivos". Autoenfoque: pasado y presente . Temas de Física Aplicada. vol. 114, págs. 547–572. Código Bib : 2009sfpp.book..547D. doi :10.1007/978-0-387-34727-1_23. ISBN 978-0-387-32147-9.
10. JS Aitchison; et al. (1992). "Observación de solitones espaciales en guías de ondas de AlGaAs". Electrón. Lett . 28 (20): 1879. Bibcode : 1992ElL....28.1879A. doi :10.1049/el:19921203.
11. GI Stegeman y M. Segev (1999). "Solitones espaciales ópticos y sus interacciones: universalidad y diversidad". Ciencia . 286 (5444): 1518-1523. doi : 10.1126/ciencia.286.5444.1518. PMID  10567250.
12. J. Beeckman; K. Neyts; X. Hutsebaut; C. Cambournac; M. Haelterman (2004). "Simulaciones y experimentos sobre condiciones de autoenfoque en células planas nemáticas de cristal líquido". Optar. Expresar . 12 (6): 1011–1018. Código Bib : 2004OExpr..12.1011B. doi : 10.1364/OPEX.12.001011 . PMID  19474916.[1][2] ^{[ enlace muerto permanente ]}
13. Okulov, A Yu (2000). "Láser de solitón espacial: geometría y estabilidad". Óptica y Espectroscopia . 89 (1): 145-147. Código Bib : 2000OptSp..89..131O. doi :10.1134/BF03356001. S2CID  122790937.
14. Okulov, A Yu (2020). "Entidades ligeras estructuradas, caos y mapas no locales". Caos, solitones y fractales . 133 (4): 109638. arXiv : 1901.09274 . Código Bib : 2020CSF...13309638O. doi : 10.1016/j.caos.2020.109638. S2CID  247759987.
15. "Solitones en Telecomunicaciones" en el libro _Nonlinear Science_ (Capítulo 3). 1997. doi : 10.17226/5833. ISBN 978-0-309-05843-8.
16. ""Haciendo olas: solitones y sus aplicaciones ópticas "de SIAM News, volumen 31, número 2" (PDF) .
17. M. Gedalin, TC Scott e YB Band, "Solitones ópticos en la ecuación de Schrödinger no lineal de orden superior", Phys. Rev. Lett. 78 : 448–451 (1997) [3][4].
18. S.Chakraborty, "Informe sobre la generación de pulsos de solitones dentro de 50 m de longitud de fibra SM mediante un método de retroalimentación inteligente no lineal inducido por alta frecuencia", Actas, Conferencia Nacional IEEE sobre Aplicaciones de Sistemas Inteligentes , Sonepat, India, págs.91–94, 2008 , ISBN 978-81-906531-0-7 . ^{[ se necesita verificación ]} 

Bibliografía

• Saleh, BEA; Teich, MC (1991). Fundamentos de Fotónica . Nueva York: John Wiley & sons, inc. ISBN 978-0-471-83965-1.
• Agrawal, Govind P. (1995). Fibra óptica no lineal (2ª ed.). San Diego (California): Prensa académica. ISBN 978-0-12-045142-5.

enlaces externos

• Propagación de solitones en SMF-28 usando la GPU