
El principio de Pareto (también conocido como la regla 80/20 , la ley de los pocos vitales y el principio de escasez de factores [1] [2] ) establece que para muchos resultados, aproximadamente el 80% de las consecuencias provienen del 20% de las causas (los "pocos vitales"). [1]
En 1941, el consultor de gestión Joseph M. Juran desarrolló el concepto en el contexto del control y la mejora de la calidad después de leer las obras del sociólogo y economista italiano Vilfredo Pareto , quien escribió en 1906 sobre la conexión 80/20 mientras enseñaba en la Universidad de Lausana . [3] En su primer trabajo, Cours d'économie politique , Pareto mostró que aproximadamente el 80% de la tierra en el Reino de Italia era propiedad del 20% de la población. El principio de Pareto solo está relacionado tangencialmente con la eficiencia de Pareto .
Matemáticamente, la regla 80/20 se describe aproximadamente mediante una distribución de ley de potencia (también conocida como distribución de Pareto ) para un conjunto particular de parámetros. Muchos fenómenos naturales se distribuyen de acuerdo con estadísticas de ley de potencia. [4] Es un adagio de la gestión empresarial que "el 80% de las ventas provienen del 20% de los clientes ". [5]
En 1941, Joseph M. Juran, un ingeniero estadounidense nacido en Rumania, se encontró con el trabajo del erudito italiano Vilfredo Pareto . Pareto señaló que aproximadamente el 80% de las tierras de Italia eran propiedad del 20% de la población. [6] [4] Juran aplicó la observación de que el 80% de un problema es causado por el 20% de las causas a los problemas de calidad. Más adelante durante su carrera, Juran prefirió describir esto como "los pocos vitales y los muchos útiles" para destacar que la contribución del 80% restante no debería descartarse por completo. [7]
La demostración del principio de Pareto se explica por el hecho de que una gran proporción de la variación del proceso está asociada a una pequeña proporción de las variables del proceso. [2] Este es un caso especial del fenómeno más amplio de las distribuciones de Pareto . Si el índice de Pareto α , que es uno de los parámetros que caracterizan una distribución de Pareto, se elige como α = log 4 5 ≈ 1,16, entonces tenemos que el 80% de los efectos provienen del 20% de las causas. [8]
El término 80/20 es sólo una abreviatura del principio general en funcionamiento. En casos individuales, la distribución podría ser más cercana a 90/10 o 70/30. Tampoco hay necesidad de que los dos números sumen el número 100, ya que son medidas de cosas diferentes. El principio de Pareto es una ilustración de una relación de " ley de potencia ", que también ocurre en fenómenos como incendios forestales y terremotos. [9] Debido a que es autosimilar en un amplio rango de magnitudes, produce resultados completamente diferentes de los fenómenos de distribución normal o gaussiana . Este hecho explica las frecuentes fallas de instrumentos financieros sofisticados, que se modelan sobre la suposición de que una relación gaussiana es apropiada para algo como los movimientos de precios de acciones. [10]
Utilizando la notación " A : B " (por ejemplo, 0,8:0,2) y con A + B = 1, se pueden calcular medidas de desigualdad como el índice de Gini (G) y el índice de Hoover (H). En este caso, ambos son iguales:
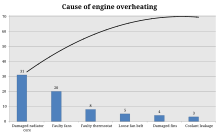
El análisis de Pareto es una técnica formal que resulta útil cuando hay muchos cursos de acción posibles que compiten por captar la atención. En esencia, el solucionador de problemas calcula el beneficio que ofrece cada acción y luego selecciona una serie de las acciones más eficaces que ofrecen un beneficio total razonablemente cercano al máximo posible.
El análisis de Pareto es una forma creativa de analizar las causas de los problemas porque ayuda a estimular el pensamiento y a organizarlo. Sin embargo, puede verse limitado por la exclusión de problemas posiblemente importantes que pueden ser pequeños al principio, pero que crecerán con el tiempo. Debe combinarse con otras herramientas analíticas, como el análisis de modos de falla y efectos y el análisis de árboles de fallas , por ejemplo. [ cita requerida ]
Esta técnica ayuda a identificar la parte principal de las causas que deben abordarse para resolver la mayoría de los problemas. Una vez identificadas las causas predominantes, se pueden utilizar herramientas como el diagrama de Ishikawa o el análisis de espina de pescado para identificar las causas fundamentales de los problemas. Si bien es común referirse a Pareto como la regla "80/20", partiendo del supuesto de que, en todas las situaciones, el 20% de las causas determinan el 80% de los problemas, esta proporción es simplemente una regla práctica conveniente y no es, ni debe considerarse, una ley inmutable de la naturaleza.
La aplicación del análisis de Pareto en la gestión de riesgos permite a la dirección centrarse en aquellos riesgos que tienen mayor impacto en el proyecto. [11]
Pasos para identificar las causas importantes utilizando la regla 80/20: [12]
La observación de Pareto estaba relacionada con la población y la riqueza . Pareto notó que aproximadamente el 80% de las tierras de Italia estaban en manos del 20% de la población. [6] Luego realizó encuestas en una variedad de otros países y descubrió, para su sorpresa, que se aplicaba una distribución similar. [ cita requerida ]
Un gráfico que demostró el efecto apareció en el Informe del Programa de las Naciones Unidas para el Desarrollo de 1992 , que mostraba que el 20% más rico de la población mundial recibe el 82,7% del ingreso mundial. [13] Sin embargo, entre las naciones, el índice de Gini muestra que las distribuciones de riqueza varían sustancialmente en torno a esta norma. [14]
El principio también se aplica a los extremos de la distribución. El físico Victor Yakovenko, de la Universidad de Maryland, College Park, y AC Silva analizaron los datos de ingresos del Servicio de Impuestos Internos de Estados Unidos de 1983 a 2001 y descubrieron que la distribución de los ingresos del 1-3% más rico de la población también sigue el principio de Pareto. [16]
En Talent: How to Identify Entrepreneurs , el economista Tyler Cowen y el empresario Daniel Gross sugieren que el Principio de Pareto se puede aplicar al papel del 20% de los individuos más talentosos en la generación de la mayor parte del crecimiento económico . [17] Según el New York Times en 1988, muchas tiendas de alquiler de videos informaron que el 80% de los ingresos provenían del 20% de las cintas de vídeo (aunque los clásicos raramente alquilados como Lo que el viento se llevó deben estar en stock para que parezca que tienen una buena selección). [18]
En informática, el principio de Pareto se puede aplicar a los esfuerzos de optimización . [19] Por ejemplo, Microsoft observó que al corregir el 20% de los errores más frecuentes, se eliminarían el 80% de los errores y fallos relacionados en un sistema determinado. [20] Lowell Arthur expresó que "el 20% del código tiene el 80% de los errores. ¡Encuéntrelos y arréglelos!" [21] También se descubrió que, en general, el 80% de un software se puede escribir en el 20% del tiempo total asignado. Por el contrario, el 20% más difícil del código requiere el 80% del tiempo. Este factor suele ser parte de la estimación COCOMO para la codificación de software. [ cita requerida ]
Los profesionales de la seguridad y la salud ocupacional utilizan el principio de Pareto para subrayar la importancia de la priorización de los peligros. Suponiendo que el 20% de los peligros representan el 80% de las lesiones, y al categorizar los peligros, los profesionales de la seguridad pueden centrarse en ese 20% de los peligros que causan el 80% de las lesiones o accidentes. Por el contrario, si se abordan los peligros en orden aleatorio, es más probable que un profesional de la seguridad solucione uno de los 80% de los peligros que representan solo una fracción del 20% restante de las lesiones. [22]
Además de garantizar prácticas eficientes de prevención de accidentes, el principio de Pareto también garantiza que los peligros se aborden en un orden económico, porque la técnica garantiza que los recursos utilizados se usen mejor para prevenir la mayor cantidad de accidentes. [23]
El principio de Pareto es la base del diagrama de Pareto , una de las herramientas clave utilizadas en el control de calidad total y en las técnicas Six Sigma . El principio de Pareto sirve como base para el análisis ABC y el análisis XYZ, ampliamente utilizados en logística y adquisiciones con el fin de optimizar el stock de bienes, así como los costos de mantenimiento y reposición de ese stock. [24] En la teoría de control de ingeniería, como en el caso de los convertidores de energía electromecánicos, el principio 80/20 se aplica a los esfuerzos de optimización. [19]
El notable éxito de las búsquedas de causas profundas basadas en la estadística se basa en una combinación de un principio empírico y lógica matemática. El principio empírico suele conocerse como el principio de Pareto. [25] Con respecto a la causalidad de la variación, este principio establece que existe una distribución no aleatoria de las pendientes de los numerosos términos (teóricamente infinitos) de la ecuación general.
Todos los términos son independientes entre sí por definición. Los factores interdependientes aparecen como términos de multiplicación. El principio de Pareto establece que el efecto del término dominante es mucho mayor que el del segundo término de mayor efecto, que a su vez es mucho mayor que el del tercero, y así sucesivamente. [26] No hay explicación para este fenómeno; por eso lo llamamos principio empírico.
La lógica matemática se conoce como el axioma de la raíz cuadrada de la suma de los cuadrados. Este establece que la variación causada por la pendiente más pronunciada debe elevarse al cuadrado y, luego, el resultado debe sumarse al cuadrado de la variación causada por la segunda pendiente más pronunciada, y así sucesivamente. La variación total observada es entonces la raíz cuadrada de la suma total de la variación causada por las pendientes individuales elevadas al cuadrado. Esto se deriva de la función de densidad de probabilidad para múltiples variables o la distribución multivariada (tratamos cada término como una variable independiente).
La combinación del principio de Pareto y el axioma de la raíz cuadrada de la suma de los cuadrados significa que el término más fuerte de la ecuación general domina totalmente la variación observada del efecto. Por lo tanto, el término más fuerte dominará los datos recopilados para la prueba de hipótesis.
En la disciplina de la ciencia de sistemas, Joshua M. Epstein y Robert Axtell crearon un modelo de simulación basado en agentes llamado Sugarscape , a partir de un enfoque de modelado descentralizado , basado en reglas de comportamiento individuales definidas para cada agente de la economía. En sus resultados surgieron la distribución de la riqueza y el principio 80/20 de Pareto, lo que sugiere que el principio es una consecuencia colectiva de estas reglas individuales. [27]
En 2009, la Agencia para la Investigación y la Calidad de la Atención Médica dijo que el 20% de los pacientes incurrieron en el 80% de los gastos de atención médica debido a enfermedades crónicas. [28] Un análisis de 2021 mostró una distribución desigual de los costos de la atención médica, y los pacientes de mayor edad y aquellos con peor salud incurrieron en más costos. [29] La regla 80/20 se ha propuesto como regla general para la distribución de la infección en eventos de superpropagación . [30] [31] Sin embargo, se ha descubierto que el grado de infecciosidad se distribuye de forma continua en la población. [31] En epidemias con superpropagación, la mayoría de los individuos infectan relativamente a pocos contactos secundarios .