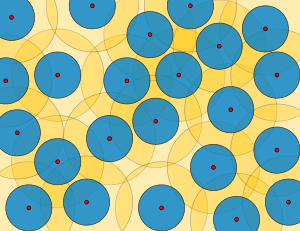
En la teoría matemática de los espacios métricos , las ε -redes , los ε -empaquetamientos , los ε -cubrimientos , los conjuntos uniformemente discretos , los conjuntos relativamente densos y los conjuntos de Delone (nombrados en honor a Boris Delone ) son varias definiciones estrechamente relacionadas de conjuntos de puntos bien espaciados , y el radio de empaquetamiento y el radio de recubrimiento de estos conjuntos miden qué tan bien espaciados están. Estos conjuntos tienen aplicaciones en la teoría de codificación , los algoritmos de aproximación y la teoría de los cuasicristales .
Si ( M , d ) es un espacio métrico, y X es un subconjunto de M , entonces el radio de empaquetamiento , r , de X es la mitad de la distancia más pequeña entre miembros distintos de X . Las bolas abiertas de radio r centradas en los puntos de X estarán todas disjuntas entre sí. El radio de empaquetamiento , R , de X es la distancia más pequeña tal que cada punto de M está dentro de la distancia R de al menos un punto en X ; es decir, R es el radio más pequeño tal que las bolas cerradas de ese radio centradas en los puntos de X tienen todo M como su unión.
Un empaquetamiento ε es un conjunto X con un radio de empaquetamiento r ≥ mi/2 (equivalentemente, distancia mínima ≥ ε ), una ε -cobertura es un conjunto X con un radio de cobertura R ≤ ε , y una ε -red es un conjunto que es a la vez un ε -empaquetamiento y una ε -cobertura ( mi/2 ≤ r ≤ R ≤ ε ).
Un conjunto es uniformemente discreto si tiene un radio de empaquetamiento distinto de cero ( 0 < r ), y relativamente denso si tiene un radio de cobertura finito ( R < ∞ ).
Un conjunto Delone es un conjunto que es uniformemente discreto y relativamente denso ( 0 < r ≤ R < ∞ ). Por lo tanto, cada ε -net es Delone, pero no viceversa. [1] [2]
Como la más restrictiva de las definiciones anteriores, las ε -redes son al menos tan difíciles de construir como los ε -empaquetamientos, ε -cubrimientos y conjuntos de Delone. Sin embargo, siempre que los puntos de M tengan un buen ordenamiento , la inducción transfinita muestra que es posible construir una ε -red N , incluyendo en N cada punto para el cual el ínfimo de distancias al conjunto de puntos anteriores en el ordenamiento sea al menos ε . Para conjuntos finitos de puntos en un espacio euclidiano de dimensión acotada, cada punto puede probarse en tiempo constante mapeándolo a una cuadrícula de celdas de diámetro ε , y usando una tabla hash para probar qué celdas cercanas ya contienen puntos de N ; por lo tanto, en este caso, una ε -red puede construirse en tiempo lineal . [3] [4]
Para espacios métricos finitos o compactos más generales, se puede utilizar un algoritmo alternativo de Teo González basado en el recorrido más lejano primero para construir una ε -red finita. Este algoritmo inicializa la red N para que esté vacía, y luego agrega repetidamente a N el punto más alejado en M desde N , rompiendo los empates arbitrariamente y deteniéndose cuando todos los puntos de M están dentro de la distancia ε de N . [5] En espacios de dimensión de duplicación acotada , el algoritmo de González se puede implementar en tiempo O( n log n ) para conjuntos de puntos con una razón polinómica entre sus distancias más lejanas y más cercanas, y aproximarse en el mismo límite de tiempo para conjuntos de puntos arbitrarios. [6]
En la teoría de códigos correctores de errores , el espacio métrico que contiene un código de bloque C consiste en cadenas de una longitud fija, digamos n , tomadas sobre un alfabeto de tamaño q (pueden considerarse como vectores ), con la métrica de Hamming . Este espacio se denota por El radio de cobertura y el radio de empaquetamiento de este espacio métrico están relacionados con la capacidad del código para corregir errores. Un ejemplo lo proporciona el juego de conmutación de Berlekamp .
Har-Peled y Raichel (2013) describen un paradigma algorítmico que denominan "net and prune" para diseñar algoritmos de aproximación para ciertos tipos de problemas de optimización geométrica definidos sobre conjuntos de puntos en espacios euclidianos . Un algoritmo de este tipo funciona realizando los siguientes pasos:
En ambos casos, el número esperado de puntos restantes disminuye en un factor constante, por lo que el tiempo está dominado por el paso de prueba. Como muestran, este paradigma se puede utilizar para construir algoritmos de aproximación rápidos para la agrupación de k centros , la búsqueda de un par de puntos con distancia mediana y varios problemas relacionados.
Se puede utilizar un sistema jerárquico de redes, llamado árbol de redes , en espacios de dimensión de duplicación acotada para construir descomposiciones de pares bien separados , llaves geométricas y vecinos más cercanos aproximados . [6] [7]
Para los puntos en el espacio euclidiano , un conjunto X es un conjunto de Meyer si es relativamente denso y su conjunto de diferencias X − X es uniformemente discreto. De manera equivalente, X es un conjunto de Meyer si tanto X como X − X son conjuntos de Delone. Los conjuntos de Meyer reciben su nombre de Yves Meyer , quien los introdujo (con una definición diferente pero equivalente basada en el análisis armónico ) como un modelo matemático para los cuasicristales . Incluyen los conjuntos puntuales de las redes , los teselados de Penrose y las sumas de Minkowski de estos conjuntos con conjuntos finitos. [8]
Las células de Voronoi de los conjuntos simétricos de Delone forman poliedros que llenan el espacio llamados plesioedros . [9]