Suavidad

Número de derivadas de una función (matemáticas)

Una función de protuberancia es una función suave con soporte compacto .

En análisis matemático , la suavidad de una función es una propiedad medida por el número de derivadas continuas ( clase de diferenciabilidad) que tiene sobre su dominio . ^[1]

Una función de clase es una función de suavidad al menos k ; es decir, una función de clase es una función que tiene una derivada k -ésima que es continua en su dominio. ${\displaystyle C^{k}}$ ${\displaystyle C^{k}}$

Una función de clase o -función (se pronuncia función C-infinita ) es una función infinitamente diferenciable , es decir, una función que tiene derivadas de todos los órdenes (esto implica que todas estas derivadas son continuas). ${\displaystyle C^{\infty }}$ ${\displaystyle C^{\infty }}$

En general, el término función suave se refiere a una función α. Sin embargo, también puede significar "suficientemente diferenciable" para el problema en cuestión. ${\displaystyle C^{\infty }}$

Clases de diferenciabilidad

La clase de diferenciabilidad es una clasificación de funciones según las propiedades de sus derivadas . Es una medida del orden más alto de derivada que existe y es continua para una función.

Consideremos un conjunto abierto en la recta real y una función definida en con valores reales. Sea k un entero no negativo . Se dice que la función es de clase de diferenciabilidad si las derivadas existen y son continuas en Si es -diferenciable en entonces está al menos en la clase ya que son continuas en Se dice que la función es infinitamente diferenciable , suave o de clase si tiene derivadas de todos los órdenes en (Por lo que todas estas derivadas son funciones continuas sobre ) ^[2] Se dice que la función es de clase o analítica , si es suave (es decir, está en la clase ) y su expansión en serie de Taylor alrededor de cualquier punto en su dominio converge a la función en alguna vecindad del punto. Existen funciones que son suaves pero no analíticas; por lo tanto, está estrictamente contenida en Las funciones Bump son ejemplos de funciones con esta propiedad. ${\displaystyle U}$ ${\displaystyle f}$ ${\displaystyle U}$ ${\displaystyle f}$ ${\displaystyle C^{k}}$ ${\displaystyle f',f'',\dots ,f^{(k)}}$ ${\displaystyle U.}$ ${\displaystyle f}$ ${\displaystyle k}$ ${\displaystyle U,}$ ${\displaystyle C^{k-1}}$ ${\displaystyle f',f'',\dots ,f^{(k-1)}}$ ${\displaystyle U.}$ ${\displaystyle f}$ ${\displaystyle C^{\infty },}$ ${\displaystyle U.}$ ${\displaystyle U.}$ ${\displaystyle f}$ ${\displaystyle C^{\omega },}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle C^{\infty }}$ ${\displaystyle C^{\omega }}$ ${\displaystyle C^{\infty }.}$

En otras palabras, la clase consta de todas las funciones continuas. La clase consta de todas las funciones diferenciables cuya derivada es continua; tales funciones se denominan continuamente diferenciables . Por lo tanto, una función es exactamente una función cuya derivada existe y es de la clase En general, las clases se pueden definir de forma recursiva declarando que es el conjunto de todas las funciones continuas y declarando que para cualquier entero positivo es el conjunto de todas las funciones diferenciables cuya derivada está en En particular, está contenido en para cada y hay ejemplos que muestran que esta contención es estricta ( ). La clase de funciones infinitamente diferenciables, es la intersección de las clases a medida que varía sobre los enteros no negativos. ${\displaystyle C^{0}}$ ${\displaystyle C^{1}}$ ${\displaystyle C^{1}}$ ${\displaystyle C^{0}.}$ ${\displaystyle C^{k}}$ ${\displaystyle C^{0}}$ ${\displaystyle C^{k}}$ ${\displaystyle k}$ ${\displaystyle C^{k-1}.}$ ${\displaystyle C^{k}}$ ${\displaystyle C^{k-1}}$ ${\displaystyle k>0,}$ ${\displaystyle C^{k}\subsetneq C^{k-1}}$ ${\displaystyle C^{\infty }}$ ${\displaystyle C^{k}}$ ${\displaystyle k}$

Ejemplos

Ejemplo: Continuo (do⁰) Pero no diferenciable

La función C ⁰ f ( x ) = x para x ≥ 0 y 0 en caso contrario.

La función g ( x ) = x ² sin(1/ x ) para x > 0 .

La función con para y es diferenciable. Sin embargo, esta función no es continuamente diferenciable. ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ ${\displaystyle f(x)=x^{2}\sin \left({\tfrac {1}{x}}\right)}$ ${\displaystyle x\neq 0}$ ${\displaystyle f(0)=0}$

Una función suave que no es analítica.

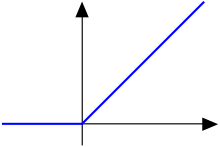
La función es continua, pero no diferenciable en x = 0 , por lo que es de clase C ⁰ , pero no de clase C ¹ . $${\displaystyle f(x)={\begin{cases}x&{\mbox{if }}x\geq 0,\\0&{\text{if }}x<0\end{cases}}}$$

Ejemplo: Diferenciable finitamente veces (do^a)

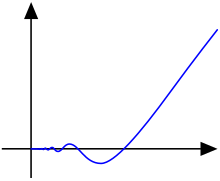
Para cada entero par k , la función es continua y k veces diferenciable en todos los x . Sin embargo, en x = 0 , no es ( k + 1) veces diferenciable, por lo que es de clase C ^k , pero no de clase C ^j donde j > k . $${\displaystyle f(x)=|x|^{k+1}}$$ ${\displaystyle f}$ ${\displaystyle f}$

Ejemplo: Diferenciable pero no continuamente diferenciable (nodo¹)

La función es diferenciable, con derivada $${\displaystyle g(x)={\begin{cases}x^{2}\sin {\left({\tfrac {1}{x}}\right)}&{\text{if }}x\neq 0,\\0&{\text{if }}x=0\end{cases}}}$$ $${\displaystyle g'(x)={\begin{cases}-{\mathord {\cos \left({\tfrac {1}{x}}\right)}}+2x\sin \left({\tfrac {1}{x}}\right)&{\text{if }}x\neq 0,\\0&{\text{if }}x=0.\end{cases}}}$$

Como oscila cuando x → 0, no es continua en cero. Por lo tanto, es diferenciable pero no de la clase C ¹ . ${\displaystyle \cos(1/x)}$ ${\displaystyle g'(x)}$ ${\displaystyle g(x)}$

Ejemplo: Diferenciable pero no Lipschitz Continuo

La función es diferenciable pero su derivada no está acotada en un conjunto compacto . Por lo tanto, es un ejemplo de una función que es diferenciable pero no localmente Lipschitz continua . $${\displaystyle h(x)={\begin{cases}x^{4/3}\sin {\left({\tfrac {1}{x}}\right)}&{\text{if }}x\neq 0,\\0&{\text{if }}x=0\end{cases}}}$$ ${\displaystyle h}$

Ejemplo: Analítico (do^ω)

La función exponencial es analítica y, por lo tanto, cae en la clase C ^ω . Las funciones trigonométricas también son analíticas donde sea que se definan, porque son combinaciones lineales de funciones exponenciales complejas y . ${\displaystyle e^{x}}$ ${\displaystyle e^{ix}}$ ${\displaystyle e^{-ix}}$

Ejemplo: Suave (do^∞) pero no Analítico (do^ω)

La función bump es suave, por lo tanto de clase C ^∞ , pero no es analítica en x = ±1 , y por lo tanto no es de clase C ^ω . La función f es un ejemplo de una función suave con soporte compacto . $${\displaystyle f(x)={\begin{cases}e^{-{\frac {1}{1-x^{2}}}}&{\text{ if }}|x|<1,\\0&{\text{ otherwise }}\end{cases}}}$$

Clases de diferenciabilidad multivariable

Una función definida en un conjunto abierto de se dice ^[3] que es de clase en , para un entero positivo , si todas las derivadas parciales existen y son continuas, para cada entero no negativo, tal que , y cada . Equivalentemente, es de clase en si la derivada de Fréchet de orden -ésimo de existe y es continua en cada punto de . Se dice que la función es de clase o si es continua en . También se dice que las funciones de clase son continuamente diferenciables . ${\displaystyle f:U\subset \mathbb {R} ^{n}\to \mathbb {R} }$ ${\displaystyle U}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle C^{k}}$ ${\displaystyle U}$ ${\displaystyle k}$ $${\displaystyle {\frac {\partial ^{\alpha }f}{\partial x_{1}^{\alpha _{1}}\,\partial x_{2}^{\alpha _{2}}\,\cdots \,\partial x_{n}^{\alpha _{n}}}}(y_{1},y_{2},\ldots ,y_{n})}$$ ${\displaystyle \alpha _{1},\alpha _{2},\ldots ,\alpha _{n}}$ ${\displaystyle \alpha =\alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}\leq k}$ ${\displaystyle (y_{1},y_{2},\ldots ,y_{n})\in U}$ ${\displaystyle f}$ ${\displaystyle C^{k}}$ ${\displaystyle U}$ ${\displaystyle k}$ ${\displaystyle f}$ ${\displaystyle U}$ ${\displaystyle f}$ ${\displaystyle C}$ ${\displaystyle C^{0}}$ ${\displaystyle U}$ ${\displaystyle C^{1}}$

Una función , definida en un conjunto abierto de , se dice que es de clase en , para un entero positivo , si todos sus componentes son de clase , donde son las proyecciones naturales definidas por . Se dice que es de clase o si es continua, o equivalentemente, si todos los componentes son continuos, en . ${\displaystyle f:U\subset \mathbb {R} ^{n}\to \mathbb {R} ^{m}}$ ${\displaystyle U}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle C^{k}}$ ${\displaystyle U}$ ${\displaystyle k}$ $${\displaystyle f_{i}(x_{1},x_{2},\ldots ,x_{n})=(\pi _{i}\circ f)(x_{1},x_{2},\ldots ,x_{n})=\pi _{i}(f(x_{1},x_{2},\ldots ,x_{n})){\text{ for }}i=1,2,3,\ldots ,m}$$ ${\displaystyle C^{k}}$ ${\displaystyle \pi _{i}}$ ${\displaystyle \pi _{i}:\mathbb {R} ^{m}\to \mathbb {R} }$ ${\displaystyle \pi _{i}(x_{1},x_{2},\ldots ,x_{m})=x_{i}}$ ${\displaystyle C}$ ${\displaystyle C^{0}}$ ${\displaystyle f_{i}}$ ${\displaystyle U}$

El espacio dedoafunciones

Sea un subconjunto abierto de la recta real. El conjunto de todas las funciones de valor real definidas en es un espacio vectorial de Fréchet , con la familia numerable de seminomas donde varía en una secuencia creciente de conjuntos compactos cuya unión es , y . ${\displaystyle D}$ ${\displaystyle C^{k}}$ ${\displaystyle D}$ $${\displaystyle p_{K,m}=\sup _{x\in K}\left|f^{(m)}(x)\right|}$$ ${\displaystyle K}$ ${\displaystyle D}$ ${\displaystyle m=0,1,\dots ,k}$

El conjunto de funciones sobre también forma un espacio de Fréchet. Se utilizan las mismas seminormas que antes, excepto que se permite abarcar todos los valores enteros no negativos. ${\displaystyle C^{\infty }}$ ${\displaystyle D}$ ${\displaystyle m}$

Los espacios anteriores ocurren naturalmente en aplicaciones donde son necesarias funciones que tienen derivadas de ciertos órdenes; sin embargo, particularmente en el estudio de ecuaciones diferenciales parciales , a veces puede ser más fructífero trabajar con los espacios de Sobolev .

Continuidad

Los términos continuidad paramétrica ( C ^k ) y continuidad geométrica ( G ⁿ ) fueron introducidos por Brian Barsky , para demostrar que la suavidad de una curva podía medirse eliminando las restricciones en la velocidad con la que el parámetro traza la curva. ^{[4] [5] [6]}

Continuidad paramétrica

La continuidad paramétrica ( C ^k ) es un concepto aplicado a las curvas paramétricas , que describe la suavidad del valor del parámetro con la distancia a lo largo de la curva. Se dice que una curva (paramétrica) es de clase C ^k , si existe y es continua en , donde las derivadas en los puntos finales y se toman como derivadas unilaterales (desde la derecha en y desde la izquierda en ). ${\displaystyle s:[0,1]\to \mathbb {R} ^{n}}$ ${\displaystyle \textstyle {\frac {d^{k}s}{dt^{k}}}}$ ${\displaystyle [0,1]}$ ${\displaystyle 0}$ ${\displaystyle 1}$ ${\displaystyle 0}$ ${\displaystyle 1}$

Como aplicación práctica de este concepto, una curva que describe el movimiento de un objeto con un parámetro de tiempo debe tener una continuidad C ¹ y su primera derivada debe ser diferenciable, para que el objeto tenga una aceleración finita. Para un movimiento más suave, como el de la trayectoria de una cámara al filmar una película, se requieren órdenes superiores de continuidad paramétrica.

Orden de continuidad paramétrica

Dos segmentos de curva de Bézier unidos que son solo C ⁰ continuos

Dos segmentos de curva de Bézier unidos de tal manera que sean C ¹ continuos

Los distintos órdenes de continuidad paramétrica se pueden describir de la siguiente manera: ^[7]

• ${\displaystyle C^{0}}$:la derivada cero es continua (las curvas son continuas)
• ${\displaystyle C^{1}}$:la derivada cero y la primera son continuas
• ${\displaystyle C^{2}}$:la derivada cero, primera y segunda son continuas
• ${\displaystyle C^{n}}$:Las derivadas 0-ésima a -ésima son continuas ${\displaystyle n}$

Continuidad geométrica

Curvas con contacto G ¹ (círculos, líneas)

${\displaystyle (1-\varepsilon ^{2})x^{2}-2px+y^{2}=0,\ p>0\ ,\varepsilon \geq 0}$
Lápiz de secciones cónicas con contacto G ² : p fijo, variable ( : círculo, : elipse, : parábola, : hipérbola) ${\displaystyle \varepsilon }$
${\displaystyle \varepsilon =0}$ ${\displaystyle \varepsilon =0.8}$ ${\displaystyle \varepsilon =1}$ ${\displaystyle \varepsilon =1.2}$

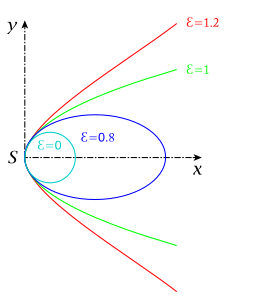
Una curva o superficie puede describirse como una superficie con continuidad, siendo α la medida creciente de suavidad. Consideremos los segmentos a cada lado de un punto en una curva: ${\displaystyle G^{n}}$ ${\displaystyle n}$

• ${\displaystyle G^{0}}$:Las curvas se tocan en el punto de unión.
• ${\displaystyle G^{1}}$:Las curvas también comparten una dirección tangente común en el punto de unión.
• ${\displaystyle G^{2}}$:Las curvas también comparten un centro de curvatura común en el punto de unión.

En general, existe continuidad si las curvas se pueden repararetrizar para tener continuidad (paramétrica). ^{[8] [9]} Una reparametrización de la curva es geométricamente idéntica a la original; solo se ve afectado el parámetro. ${\displaystyle G^{n}}$ ${\displaystyle C^{n}}$

De manera equivalente, dos funciones vectoriales y tales que tienen continuidad en el punto donde se encuentran si satisfacen ecuaciones conocidas como restricciones beta. Por ejemplo, las restricciones beta para la continuidad son: ${\displaystyle f(t)}$ ${\displaystyle g(t)}$ ${\displaystyle f(1)=g(0)}$ ${\displaystyle G^{n}}$ ${\displaystyle G^{4}}$

${\displaystyle {\begin{aligned}g^{(1)}(0)&=\beta _{1}f^{(1)}(1)\\g^{(2)}(0)&=\beta _{1}^{2}f^{(2)}(1)+\beta _{2}f^{(1)}(1)\\g^{(3)}(0)&=\beta _{1}^{3}f^{(3)}(1)+3\beta _{1}\beta _{2}f^{(2)}(1)+\beta _{3}f^{(1)}(1)\\g^{(4)}(0)&=\beta _{1}^{4}f^{(4)}(1)+6\beta _{1}^{2}\beta _{2}f^{(3)}(1)+(4\beta _{1}\beta _{3}+3\beta _{2}^{2})f^{(2)}(1)+\beta _{4}f^{(1)}(1)\\\end{aligned}}}$

donde , , y son arbitrarios, pero están restringidos a ser positivos. ^{[8] : 65} En el caso , esto se reduce a y , para un escalar (es decir, la dirección, pero no necesariamente la magnitud, de los dos vectores es igual). ${\displaystyle \beta _{2}}$ ${\displaystyle \beta _{3}}$ ${\displaystyle \beta _{4}}$ ${\displaystyle \beta _{1}}$ ${\displaystyle n=1}$ ${\displaystyle f'(1)\neq 0}$ ${\displaystyle f'(1)=kg'(0)}$ ${\displaystyle k>0}$

Si bien puede resultar obvio que una curva necesitaría continuidad para parecer suave, para lograr una buena estética , como la que se busca en la arquitectura y el diseño de autos deportivos , se requieren niveles más altos de continuidad geométrica. Por ejemplo, los reflejos en la carrocería de un automóvil no se verán suaves a menos que la carrocería tenga continuidad. ^{[ cita requerida ]} ${\displaystyle G^{1}}$ ${\displaystyle G^{2}}$

Un rectángulo redondeado (con arcos circulares de noventa grados en las cuatro esquinas) tiene continuidad, pero no tiene continuidad. Lo mismo sucede con un cubo redondeado , con octantes de una esfera en sus esquinas y cuartos de cilindro a lo largo de sus bordes. Si se requiere una curva editable con continuidad, generalmente se eligen splines cúbicos ; estas curvas se utilizan con frecuencia en el diseño industrial . ${\displaystyle G^{1}}$ ${\displaystyle G^{2}}$ ${\displaystyle G^{2}}$

Otros conceptos

Relación con la analiticidad

Si bien todas las funciones analíticas son "suaves" (es decir, tienen todas las derivadas continuas) en el conjunto en el que son analíticas, ejemplos como las funciones de protuberancia (mencionadas anteriormente) muestran que lo inverso no es cierto para las funciones en los números reales: existen funciones reales suaves que no son analíticas. Se pueden hacer ejemplos simples de funciones que son suaves pero no analíticas en ningún punto por medio de las series de Fourier ; otro ejemplo es la función Fabius . Aunque podría parecer que tales funciones son la excepción más que la regla, resulta que las funciones analíticas están muy dispersas entre las suaves; más rigurosamente, las funciones analíticas forman un subconjunto exiguo de las funciones suaves. Además, para cada subconjunto abierto A de la línea real, existen funciones suaves que son analíticas en A y en ningún otro lugar ^{[ cita requerida ]} .

Es útil comparar la situación con la de la ubicuidad de los números trascendentes en la recta real. Tanto en la recta real como en el conjunto de funciones suaves, los ejemplos que se nos ocurren a primera vista (números algebraicos/racionales y funciones analíticas) se comportan mucho mejor que la mayoría de los casos: los números trascendentes y en ningún caso las funciones analíticas tienen medida completa (sus complementos son escasos).

La situación así descrita contrasta marcadamente con las funciones complejas diferenciables. Si una función compleja es diferenciable sólo una vez en un conjunto abierto, es infinitamente diferenciable y analítica en ese conjunto ^{[ cita requerida ]} .

Particiones lisas de la unidad

Las funciones suaves con soporte cerrado dado se utilizan en la construcción de particiones suaves de la unidad (véase glosario de particiones de la unidad y topología ); éstas son esenciales en el estudio de variedades suaves , por ejemplo para mostrar que las métricas de Riemann se pueden definir globalmente a partir de su existencia local. Un caso simple es el de una función de protuberancia en la recta real, es decir, una función suave f que toma el valor 0 fuera de un intervalo [ a , b ] y tal que $${\displaystyle f(x)>0\quad {\text{ for }}\quad a<x<b.\,}$$

Dado un número de intervalos superpuestos en la línea, se pueden construir funciones de relieve en cada uno de ellos, y en intervalos semiinfinitos y para cubrir toda la línea, de modo que la suma de las funciones sea siempre 1. ${\displaystyle (-\infty ,c]}$ ${\displaystyle [d,+\infty )}$

De lo que se acaba de decir, las particiones de la unidad no se aplican a las funciones holomorfas ; su comportamiento diferente en relación con la existencia y la continuación analítica es una de las raíces de la teoría de haces . Por el contrario, los haces de funciones lisas tienden a no contener mucha información topológica.

Funciones suaves en y entre colectores

Dada una variedad suave , de dimensión y un atlas , entonces un mapa es suave en si para todo existe un gráfico tal que y es una función suave desde un entorno de en hasta (todas las derivadas parciales hasta un orden dado son continuas). La suavidad se puede comprobar con respecto a cualquier gráfico del atlas que contiene, ya que los requisitos de suavidad en las funciones de transición entre gráficos garantizan que si es suave cerca de en un gráfico, será suave cerca de en cualquier otro gráfico. ${\displaystyle M}$ ${\displaystyle m,}$ ${\displaystyle {\mathfrak {U}}=\{(U_{\alpha },\phi _{\alpha })\}_{\alpha },}$ ${\displaystyle f:M\to \mathbb {R} }$ ${\displaystyle M}$ ${\displaystyle p\in M}$ ${\displaystyle (U,\phi )\in {\mathfrak {U}},}$ ${\displaystyle p\in U,}$ ${\displaystyle f\circ \phi ^{-1}:\phi (U)\to \mathbb {R} }$ ${\displaystyle \phi (p)}$ ${\displaystyle \mathbb {R} ^{m}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle p,}$ ${\displaystyle f}$ ${\displaystyle p}$ ${\displaystyle p}$

Si es una función de a una variedad -dimensional , entonces es suave si, para cada hay una gráfica que contiene a y una gráfica que contiene a tal que y es una función suave de ${\displaystyle F:M\to N}$ ${\displaystyle M}$ ${\displaystyle n}$ ${\displaystyle N}$ ${\displaystyle F}$ ${\displaystyle p\in M,}$ ${\displaystyle (U,\phi )}$ ${\displaystyle p,}$ ${\displaystyle (V,\psi )}$ ${\displaystyle F(p)}$ ${\displaystyle F(U)\subset V,}$ ${\displaystyle \psi \circ F\circ \phi ^{-1}:\phi (U)\to \psi (V)}$ ${\displaystyle \mathbb {R} ^{n}.}$

Los mapas suaves entre variedades inducen mapas lineales entre espacios tangentes : para , en cada punto el empuje hacia adelante (o diferencial) asigna vectores tangentes en a vectores tangentes en : y en el nivel del fibrado tangente , el empuje hacia adelante es un homomorfismo de fibrado vectorial : El dual del empuje hacia adelante es el retroceso , que "tira" de los covectores de vuelta a los covectores de y de las -formas a las -formas: De esta manera, las funciones suaves entre variedades pueden transportar datos locales , como campos vectoriales y formas diferenciales , de una variedad a otra, o hacia abajo al espacio euclidiano donde los cálculos como la integración se entienden bien. ${\displaystyle F:M\to N}$ ${\displaystyle p}$ ${\displaystyle F(p)}$ ${\displaystyle F_{*,p}:T_{p}M\to T_{F(p)}N,}$ ${\displaystyle F_{*}:TM\to TN.}$ ${\displaystyle N}$ ${\displaystyle M,}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle F^{*}:\Omega ^{k}(N)\to \Omega ^{k}(M).}$

Las preimágenes y los empujes hacia delante a lo largo de funciones suaves no son, en general, variedades sin suposiciones adicionales. Las preimágenes de puntos regulares (es decir, si la diferencial no se anula en la preimagen) son variedades; este es el teorema de la preimagen . De manera similar, los empujes hacia delante a lo largo de incrustaciones son variedades. ^[10]

Funciones suaves entre subconjuntos de variedades

Existe una noción correspondiente de función suavizada para subconjuntos arbitrarios de variedades. Si es una función cuyo dominio y rango son subconjuntos de variedades y respectivamente. se dice que es suavizada si para todo hay un conjunto abierto con y una función suavizada tal que para todo ${\displaystyle f:X\to Y}$ ${\displaystyle X\subseteq M}$ ${\displaystyle Y\subseteq N}$ ${\displaystyle f}$ ${\displaystyle x\in X}$ ${\displaystyle U\subseteq M}$ ${\displaystyle x\in U}$ ${\displaystyle F:U\to N}$ ${\displaystyle F(p)=f(p)}$ ${\displaystyle p\in U\cap X.}$

Véase también

• Discontinuidad  – Análisis matemático de puntos discontinuosPages displaying short descriptions of redirect targets
• Lema de Hadamard
• Función suave no analítica  : funciones matemáticas que son suaves pero no analíticas
• Función cuasi-analítica
• Singularidad (matemáticas)  – Punto donde una función, una curva u otro objeto matemático no se comporta regularmente
• Sinuosidad  : relación entre la longitud del arco y la distancia en línea recta entre dos puntos en una función de tipo onda.
• Esquema suave  – tipo de esquemaPages displaying wikidata descriptions as a fallback
• Número liso  : entero que tiene solo factores primos pequeños (teoría de números)
• Suavizado  : ajuste de una función de aproximación a los datos
• Spline  – Función matemática definida por partes mediante polinomios
• Cartografía de Sobolev

Referencias

1. Weisstein, Eric W. "Función suave". mathworld.wolfram.com . Archivado desde el original el 2019-12-16 . Consultado el 2019-12-13 .
2. Warner, Frank W. (1983). Fundamentos de variedades diferenciables y grupos de Lie. Springer. p. 5 [Definición 1.2]. ISBN 978-0-387-90894-6Archivado desde el original el 1 de octubre de 2015. Consultado el 28 de noviembre de 2014 .
3. Henri Cartan (1977). Curso de cálculo diferencial . París: Hermann.
4. Barsky, Brian A. (1981). El beta-spline: una representación local basada en parámetros de forma y medidas geométricas fundamentales (Ph.D.). Universidad de Utah, Salt Lake City, Utah.
5. Brian A. Barsky (1988). Gráficos por computadora y modelado geométrico utilizando beta-splines . Springer-Verlag, Heidelberg. ISBN 978-3-642-72294-3.
6. Richard H. Bartels; John C. Beatty; Brian A. Barsky (1987). Introducción a las splines para su uso en gráficos de computadora y modelado geométrico . Morgan Kaufmann. Capítulo 13. Continuidad paramétrica frente a continuidad geométrica. ISBN 978-1-55860-400-1.
7. van de Panne, Michiel (1996). "Curvas paramétricas". Notas en línea de otoño de 1996. Universidad de Toronto, Canadá. Archivado desde el original el 26 de noviembre de 2020. Consultado el 1 de septiembre de 2019 .
8. Barsky, Brian A.; DeRose, Tony D. (1989). "Continuidad geométrica de curvas paramétricas: tres caracterizaciones equivalentes". IEEE Computer Graphics and Applications . 9 (6): 60–68. doi :10.1109/38.41470. S2CID  17893586.
9. Hartmann, Erich (2003). "Geometría y algoritmos para el diseño asistido por computadora" (PDF) . Universidad Técnica de Darmstadt . pag. 55. Archivado (PDF) desde el original el 23 de octubre de 2020 . Consultado el 31 de agosto de 2019 .
10. Guillemin, Victor; Pollack, Alan (1974). Topología diferencial . Englewood Cliffs: Prentice-Hall. ISBN 0-13-212605-2.