
El problema del lobo, la cabra y el repollo es un rompecabezas relacionado con el cruce de un río . Se remonta al menos al siglo IX [1] y ha entrado en el folclore de varias culturas. [2] [3]
Un granjero con un lobo , una cabra y un repollo debe cruzar un río en bote. El bote solo puede llevar al granjero y un solo objeto. Si se los deja solos juntos, el lobo se comerá a la cabra, o la cabra se comerá el repollo. ¿Cómo pueden cruzar el río sin comer nada?
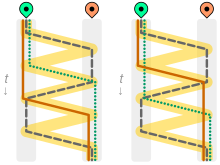
El primer paso que se debe dar es dejar que la cabra cruce el río, ya que cualquier otra acción dará como resultado que se coman la cabra o la col. Cuando el granjero regresa al lado original, tiene la opción de cruzar con el lobo o la col. Si cruza con el lobo, tendrá que volver a buscar la col, lo que hará que el lobo se coma a la cabra. Si cruza con la col en segundo lugar, tendrá que volver a buscar al lobo, lo que hará que la cabra se coma la col. El dilema se resuelve cruzando con el lobo (o la col) y trayendo a la cabra de vuelta . Ahora puede cruzar con la col (o el lobo) y finalmente regresar a buscar a la cabra.

Sus acciones en la solución se resumen en los siguientes pasos:
Hay siete cruces: cuatro hacia delante y tres hacia atrás.
La clave de la solución es darse cuenta de que se pueden recuperar las cosas (como se ha subrayado anteriormente). Esto no suele quedar claro en la redacción de la historia, pero nunca está prohibido. Saber esto hará que el problema sea fácil de resolver incluso para niños pequeños. El objetivo del rompecabezas no es solo programar tareas, sino pensar de forma creativa, de forma similar al rompecabezas de los nueve puntos .

El rompecabezas es uno de varios rompecabezas de cruce de río , donde el objetivo es mover un conjunto de elementos a través de un río sujeto a varias restricciones.
En la primera aparición conocida de este problema, en el manuscrito medieval Propositiones ad Acuendos Juvenes , los tres objetos son un lobo, una cabra y un repollo, pero también existen otras variaciones cosméticas del rompecabezas, como: lobo, oveja y repollo; [4] [2] , p. 26 zorro, pollo y grano; [5] zorro, ganso y maíz; [6] y pantera, cerdo y gachas. [7] La lógica del rompecabezas, en el que hay tres objetos, A , B y C , tales que ni A y B ni B y C pueden dejarse juntos, sigue siendo la misma.
Otra versión del rompecabezas que surge de una leyenda china está registrada en un panel pintado del siglo XVIII por el artista japonés Maruyama Ōkyo , en la colección del Museo Británico. Según la leyenda, cuando un tigre tiene tres cachorros, uno de ellos será un leopardo en lugar de un tigre, y más feroz que los otros. Siguiendo esta leyenda, el tema de un tigre con sus cachorros se convirtió en un tema tradicional para el arte en el este de Asia. [8] La representación de Ōkyo muestra a la familia de tigres cruzando un río, con la madre llevando un cachorro a través del río a la vez. Esto representa un rompecabezas equivalente al rompecabezas del lobo, la cabra y el repollo, preguntando cómo la madre puede hacer esto sin dejar al cachorro de leopardo solo con ninguno de los otros cachorros de tigre. [9] La misma variación del rompecabezas también se ha registrado como un koan de Ryōan-ji , un templo zen en Kioto . [10]
El rompecabezas se ha encontrado en el folclore de los afroamericanos, Camerún, las islas de Cabo Verde, Dinamarca, Etiopía, Ghana, Italia, Rumania, Rusia, Escocia, Sudán, Uganda, Zambia y Zimbabue. [2] , pp. 26–27; [11] Se le ha dado el número de índice H506.3 en el índice de motivos de literatura popular de Stith Thompson , y es ATU 1579 en el sistema de clasificación de Aarne–Thompson . [12]
El rompecabezas era uno de los favoritos de Lewis Carroll , [13] y ha sido reimpreso en varias colecciones de matemáticas recreativas . [2] , pág. 26.
En sus memorias de Las mil y una noches, Encuentros con hombres notables , el mago metafísico GI Gurdjieff cita este acertijo como "El lobo, la cabra y la col". Señala: "Este acertijo popular muestra claramente que... no sólo por medio del ingenio que todo hombre normal debería tener, sino que además no debe ser perezoso ni escatimar fuerzas, sino que debe cruzar el río más veces para alcanzar su objetivo".
Variaciones del rompecabezas también aparecen en el juego de aventuras Broken Sword: The Sleeping Dragon , el juego de rompecabezas de Nintendo DS El profesor Layton y la villa misteriosa , y en el episodio de Los Simpsons " Gone Maggie Gone ", donde Homer tiene que cruzar un río con Maggie , la pequeña ayudante de Santa Claus , y un frasco de veneno para ratas que parece caramelo. En el episodio de la Clase 3000 "Westley Side Story", Sunny y sus estudiantes realizan un ejercicio similar que involucra un pollo, un coyote y un saco de maíz. El episodio de Between the Lions "Farmer Ken's Puzzle" retrata cómo se convierte en un juego de computadora con un gato, una gallina y un saco de semillas.
En el episodio de Bull "Justicia para Cable", Benny comienza un acertijo con "un hombre tiene un zorro, un pato y una bolsa de frijoles". Bull inexplicablemente declara "No hay respuesta", y todos le creen. [14]
En algunas partes de África se han encontrado variantes del rompecabezas en las que el barco puede llevar dos objetos en lugar de uno solo. Cuando el rompecabezas se debilita de esta manera es posible introducir la restricción adicional de que no se pueden dejar juntos dos objetos, incluidos A y C. [2] , p. 27.
En el episodio "Time Amok" de Star Trek: Prodigy , una versión holográfica de Kathryn Janeway emplea la historia (aquí contada como el problema del pollo, el zorro y el grano ) para enseñar a la tripulación del USS Protostar cómo trabajar en conjunto.