Puentes capilares

Superficie minimizada del líquido que entra en contacto con dos objetos mojados

Un puente capilar es una superficie minimizada de líquido o membrana creada entre dos cuerpos rígidos de forma arbitraria. Los puentes capilares también pueden formarse entre dos líquidos. ^[1] Plateau definió una secuencia de formas capilares ^[2] conocidas como (1) nodoide con 'cuello', (2) catenoide , (3) onduloide con 'cuello', (4) cilindro , (5) onduloide con 'cadera', (6) esfera y (7) nodoide con 'cadera' . La presencia de un puente capilar, dependiendo de sus formas, puede conducir a atracción o repulsión entre los cuerpos sólidos. Los casos más simples de ellos son los axisimétricos. Distinguimos tres clases importantes de puentes, dependiendo de las formas de las superficies de los cuerpos conectados:

• dos superficies planas (fig.1)

Fig.1 Puente capilar cóncavo entre dos planos (representación esquemática)

• superficie plana y partícula esférica (fig. 2)

Fig.2 Puente capilar cóncavo entre partículas y superficie plana (representación esquemática)

• dos partículas esféricas (en general, las partículas pueden no ser de igual tamaño, fig. 3)

Fig.3 Puente capilar cóncavo entre dos partículas (representación esquemática)

Los puentes capilares y sus propiedades también pueden verse influenciados por la gravedad terrestre y por las propiedades de las superficies que forman los puentes. La sustancia que forma el puente puede ser un líquido o un gas. El límite que los encierra se denomina interfase ( superficie capilar ). La interfase se caracteriza por una tensión superficial particular .

Historia

Los puentes capilares se han estudiado durante más de 200 años. La cuestión fue planteada por primera vez por Josef Louis Lagrange en 1760, y el interés se extendió aún más por el astrónomo y matemático francés C. Delaunay . ^[3] Delaunay encontró una clase completamente nueva de superficies axialmente simétricas de curvatura media constante . La formulación y la prueba de su teorema tuvieron una larga historia. Comenzó con la proposición de Euler ^[4] de una nueva figura, llamada catenoide . (Mucho más tarde, Kenmotsu ^[5] resolvió las complejas ecuaciones no lineales, describiendo esta clase de superficies. Sin embargo, su solución es de poca importancia práctica porque no tiene interpretación geométrica.) J. Plateau demostró la existencia de tales formas con límites dados. El problema fue nombrado en su honor el problema de Plateau . ^[6]
Muchos científicos contribuyeron a la solución del problema. Uno de ellos es Thomas Young. ^[7] Pierre Simon Laplace aportó la noción de tensión capilar. Laplace incluso formuló la condición ampliamente conocida hoy en día para el equilibrio mecánico entre dos fluidos, dividido por una superficie capilar P _γ = Δ P es decir, la presión capilar entre dos fases se equilibra con su diferencia de presión adyacente.
Myshkis y Babskii completan un estudio general sobre el comportamiento del puente capilar en el campo de la gravedad. ^[8]
En el siglo pasado, se hicieron muchos esfuerzos para estudiar las fuerzas superficiales que impulsan los efectos capilares del puente. Se estableció que estas fuerzas resultan de fuerzas intermoleculares y se vuelven significativas en espacios de fluido delgados (<10 nm) entre dos superficies. ^{[9] [10]}
La inestabilidad de los puentes capilares fue discutida por primera vez por Rayleigh . ^[11] Demostró que un chorro de líquido o una superficie cilíndrica capilar se volvía inestable cuando la relación entre su longitud, H y el radio R , se vuelve mayor que 2π. En estas condiciones de pequeñas perturbaciones sinusoidales con una longitud de onda mayor que su perímetro, el área de la superficie del cilindro se vuelve mayor que la del cilindro no perturbado con el mismo volumen y, por lo tanto, se vuelve inestable. Más tarde, Hove ^[12]Formuló los requisitos variacionales para la estabilidad de superficies capilares axisimétricas (ilimitadas) en ausencia de gravedad y con perturbaciones limitadas a un volumen constante. Primero resolvió la ecuación de Young-Laplace para formas de equilibrio y demostró que la condición de Legendre para la segunda variación siempre se satisface. Por lo tanto, la estabilidad está determinada por la ausencia de valor propio negativo de la ecuación de Young-Laplace linealizada. Este enfoque de determinación de la estabilidad a partir de la segunda variación se utiliza ahora ampliamente. ^[8] Los métodos de perturbación se volvieron muy exitosos a pesar de que la naturaleza no lineal de la interacción capilar puede limitar su aplicación. Otros métodos ahora incluyen simulación directa. ^{[13] [14]} Hasta ese momento, la mayoría de los métodos para la determinación de la estabilidad requerían el cálculo del equilibrio como base para las perturbaciones. Surgió una nueva idea de que la estabilidad puede deducirse de los estados de equilibrio. ^{[15] [16]} La proposición fue probada además por Pitts ^[17] para volumen constante axisimétrico. En los años siguientes, Vogel ^{[18] [19]} amplió la teoría. Examinó el caso de puentes capilares axisimétricos con volúmenes constantes y los cambios de estabilidad corresponden a puntos de giro. El desarrollo reciente de la teoría de la bifurcación demostró que el intercambio de estabilidad entre puntos de giro y puntos de ramificación es un fenómeno general. ^{[20] [21]}

Aplicaciones y ocurrencias

Estudios recientes indican que los antiguos egipcios usaban las propiedades de la arena para crear puentes capilares al aplicar agua sobre ella. ^[22] De esta manera, reducían la fricción de la superficie y eran capaces de mover estatuas y piedras pesadas de las pirámides. Algunas artes contemporáneas, como el arte con arena , también están estrechamente relacionadas con la capacidad del agua para unir partículas. En la microscopía de fuerza atómica , cuando uno trabaja en un entorno de mayor humedad, sus estudios pueden verse afectados por la aparición de puentes capilares de tamaño nanométrico. ^[23] Estos puentes aparecen cuando la punta de trabajo se acerca a la muestra estudiada. Los puentes capilares también juegan un papel importante en el proceso de soldadura . ^[24]

• 
  Esquema de la tumba de Djehutihotep que representa el transporte de una estatua colosal
• 
  Fuerza Aérea de Estados Unidos
• 
  Soldadura
• 
  Rana arbórea de labios blancos

Los puentes capilares también están muy extendidos en la naturaleza. Insectos, moscas, saltamontes y ranas arbóreas son capaces de adherirse a superficies verticales rugosas debido a su capacidad de inyectar líquido humectante en el área de contacto entre la almohadilla y el sustrato. De esta manera se crea una interacción atractiva de largo alcance debido a la formación de puentes capilares. ^[25] Muchos problemas médicos relacionados con enfermedades respiratorias y la salud de las articulaciones del cuerpo dependen de pequeños puentes capilares. ^[26] Los puentes líquidos se utilizan ahora comúnmente en el crecimiento de cultivos celulares debido a la necesidad de imitar el trabajo de los tejidos vivos en la investigación científica. ^{[27] [28]}

Ecuaciones generales

La solución general para el perfil del capilar se conoce a partir de la consideración de la curvatura onduloide o nodoide . ^[29]
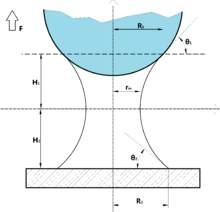
Supongamos el siguiente sistema de coordenadas cilíndricas: z muestra el eje de revolución; r representa la coordenada radial y φ es el ángulo entre la normal y el eje z positivo . El nodoide tiene tangentes verticales en r = r ₁ y r = r ₂ y tangente horizontal en r = r ₃ . Cuando φ es el ángulo entre la normal a la interfaz y el eje z positivo , entonces φ es igual a 90°, 0°, -90° para el nodoide.

La ecuación de Young-Laplace se puede escribir en una forma conveniente para la integración para simetría axial:

donde R ₁ , R ₂ son los radios de curvatura y γ es la tensión superficial interfacial.
La integración de la ecuación se denomina primera integral y da como resultado:

Desde:

Se encuentra:

Después de la integración, la ecuación obtenida se llama segunda integral :

donde: F y E son integrales elípticas de primer y segundo tipo, y φ está relacionado con r según ${\textstyle k^{2}={\frac {r_{1}^{2}-r_{2}^{2}}{r_{1}^{2}}}}$

${\displaystyle \sin ^{2}\phi ={\frac {r^{2}-r_{2}^{2}}{k^{2}r^{2}}}}$.

El onduloide sólo tiene tangentes verticales en r = r ₁ y r = r ₂ , donde φ = + 90. De manera completamente análoga:

La segunda integral para el onduloide se obtiene:

donde la relación entre los parámetros k y φ se define de la misma manera que antes. En el caso límite r ₁ = 0, tanto el nodoide como el onduloide consisten en una serie de esferas. Cuando r ₁ = r ₂ . El último y muy interesante caso límite es el catenoide . La ecuación de Laplace se reduce a:

Su integración se puede representar de una forma muy conveniente, en un sistema de coordenadas cilíndricas, llamada ecuación catenaria : ^[29]

Fig. 4. Dominio de existencia de catenoide (1) la altura está escalada por el radio R, (2) la altura está escalada por la raíz cúbica del volumen (solo válido para puentes capilares de C=0)

La ecuación (9) es importante porque muestra de forma simplificada todos los problemas relacionados con los puentes capilares. Al dibujarlos en coordenadas adimensionales, se muestra un máximo que distingue dos ramas. Una de ellas es energéticamente favorable y surge en estática, mientras que la otra (en línea discontinua) no es energéticamente favorable. El máximo es importante porque, al estirar el puente capilar en una dirección de cuasi-equilibrio, si se alcanza el máximo, se produce la rotura. Se pueden formar catenoides con dimensiones energéticamente desfavorables durante el proceso de estiramiento/prensado dinámico. ^[30] La presión capilar cero C = 0 es natural para el catenoide clásico (superficie de jabón capilar estirada entre dos anillos coaxiales). Cuando el puente capilar típico llega al estado catenoidal de C = 0, a pesar de que sus propiedades superficiales son las mismas que las del catenoide clásico, es más apropiado presentarlo como escalado por la raíz cúbica de su volumen en lugar del radio, R .

La solución de la segunda integral es diferente en los casos de puentes capilares oblatos (nodoide y onduloide):

donde: F y E son nuevamente integrales elípticas de primer y segundo tipo, y φ está relacionada con r según: . Es importante notar que todas las curvas descritas se encuentran al rodar una sección cónica sin deslizamiento a lo largo del eje z . El onduloide se describe por el foco de la elipse rodante, que puede degenerar en una línea, una esfera o una parábola, dando lugar a los casos límite correspondientes. De manera similar, un nodoide se describe por el foco de una hipérbola rodante. ${\textstyle k^{2}={\frac {r_{2}^{2}-r_{1}^{2}}{r_{2}^{2}}}}$ ${\textstyle \sin ^{2}\phi ={\frac {r_{2}^{2}-r^{2}}{k^{2}r_{2}^{2}}}}$

En la tabla 11.1 del libro de Kralchevsky y Nagayama se ofrece un resumen bien sistematizado de las formas de los puentes capilares. ^[2]

Estática entre dos superficies planas

El equilibrio mecánico comprende el equilibrio de presión en la interfaz líquido/gas y la fuerza externa sobre las placas, Δ P , que equilibra la atracción o repulsión capilar, es decir . Si se descuidan los efectos de la gravedad y otros campos externos, el equilibrio de presión es Δ P = P _i - P _e (los índices "i" y "e" denotan respectivamente las presiones interna y externa). En caso de simetría axial, la ecuación para la presión capilar toma la forma: ${\displaystyle P_{\gamma }}$ ${\displaystyle \Delta P=P_{\gamma }}$

donde γ es la tensión interfacial líquido/gas; r es la coordenada radial y φ es el ángulo entre el eje de simetría y la normal a la generatriz de la interfase.
La primera integral se obtiene fácilmente con respecto a la presión capilar adimensional en el contacto con la superficie:

donde , el radio adimensional en el contacto es y θ es el ángulo de contacto. La relación muestra que la presión capilar puede ser positiva o negativa. La forma de los puentes capilares está determinada por la ecuación: ^[2] ${\textstyle C=P_{\gamma }{\frac {r_{m}}{2\gamma }}}$ ${\textstyle X={\frac {R}{r_{m}}}}$

donde la ecuación se obtiene después de realizar la sustitución en la ecuación ( 11 ) y se introduce la escala. ${\textstyle \sin \phi ={\frac {dy}{dx}}\cos \phi }$ ${\textstyle x={\frac {r}{r_{m}}}}$

Puente líquido fino

A diferencia de los casos en los que aumenta la altura de los puentes capilares, que plantean una variedad de formas de perfil, el aplanamiento (adelgazamiento) hacia el espesor cero tiene un carácter mucho más universal. La universalidad aparece cuando H << R (fig. 1). La ecuación (11) puede escribirse: ^[31]

La generatriz converge a la ecuación:

Al integrar, la ecuación da como resultado:

Fig. 5. Puente líquido delgado

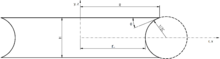
Los radios circulares adimensionales 1/2C coinciden con los radios de curvatura del puente capilar. El signo positivo '+' representa el perfil generatriz del puente cóncavo y el negativo '-', oblato. Para los puentes capilares convexos, la generatriz circular se mantiene hasta que se alcanza el límite del dominio de definición durante el estiramiento. Cerca del comienzo de la cinética de rotura autoiniciada, el perfil del puente evoluciona en consecuencia a una elipse, una parábola y posiblemente a una hipérbola. ^[32]

Definición de dominio

Las observaciones, presentadas en la figura 5, indican que se puede definir un dominio de existencia de puentes capilares. Por lo tanto, si se estira un puente líquido, podría interrumpir su existencia no solo por el aumento de las inestabilidades, sino también por alcanzar algunos puntos en los que la forma ya no puede existir. La estimación del dominio de definición requiere la manipulación de ecuaciones integradas para la altura del puente capilar y su volumen. Ambos son integrables, pero las integrales son impropias. El método aplicado incluye la división de las integrales en dos partes: singular pero integrable analíticamente y regular pero integrable solo de forma numérica.
Después de la integración, se obtiene la altura del puente capilar ^[31].

De manera similar para el radio de contacto R , se obtiene la ecuación integrada ^[31]

donde y ${\displaystyle \beta \left(C\right)=\left[1-{\frac {\left(1-2C\right)}{2C^{2}}}\right]}$ ${\displaystyle \alpha \left(C,X\right)={\frac {1}{2C}}\arcsin \left[\beta \left(C\right)-X^{2}{\frac {2C^{2}}{1-2C}}\right]}$

Fig. 6. Isógonas que muestran puentes capilares en el dominio estático, la curva roja muestra el estado catenoidal de C=0

En la figura 6 se muestra el número de estados estáticos estables del puente capilar líquido, representados por dos parámetros característicos: (i) altura adimensional que se obtiene escalando la altura del puente capilar por la raíz cúbica de su volumen Ec. ( 16 ) y (ii) su radio, también escalado por la raíz cúbica del volumen, Ec. ( 17 ). Las soluciones parcialmente analíticas, obtenidas para estos dos parámetros, se presentan arriba. Las soluciones difieren de alguna manera del enfoque ampliamente aceptado de Plateau [por funciones elípticas, Ec. ( 7 )], porque ofrecen un enfoque numérico conveniente para la integración de integrales regulares, mientras que la parte irregular de la ecuación se integró analíticamente. Estas soluciones se convirtieron además en una base para la predicción del estiramiento y la rotura de puentes capilares en cuasi-equilibrio para ángulos de contacto inferiores a 45° . La implementación práctica permite identificar no solo el final del dominio de definición sino también el comportamiento exacto durante el estiramiento del puente capilar, ^[32] porque en coordenadas el estiramiento forma una línea inclinada, donde el ángulo de inclinación es proporcional al ángulo de contacto. ${\textstyle \left(0\leq \theta \leq {\frac {\pi }{4}}\right)}$ ${\textstyle {\frac {H}{r_{m}}}\sim \ln \left({\frac {R}{r_{m}}}\right)}$

Puente capilar cóncavo

El caso del puente capilar cóncavo se presenta mediante isógonos para ángulos de contacto a continuación en la figura 6. Los isógonos muestran un máximo bien definido . Este máximo se indica mediante un punto para cada isógono. Nuevamente, de manera similar a un catenoide simple, separa dos ramas. La rama izquierda es energéticamente favorable mientras que la derecha es energéticamente desfavorable. ${\textstyle {\frac {\pi }{2}}}$ ${\textstyle \left(0\leq \theta <{\frac {\pi }{2}}\right)}$ ${\textstyle {\frac {dH^{*}}{dR^{*}}}\equiv {\frac {dH}{dR}}=0}$

Puente capilar cilíndrico

Este caso es bien analizado por Rayleigh. Nótese que el dominio de definición en su caso no muestra limitaciones y tiende al infinito, fig. 6, . Sin embargo, la rotura de puentes capilares cilíndricos se observa habitualmente. Tiene lugar como resultado de una inestabilidad bien estudiada conocida ahora como inestabilidad de Rayleigh . ^[11] El dominio de definición para la isógona de 90° se muestra en la fig. 6 mediante una línea discontinua. ${\textstyle \left(\theta ={\frac {\pi }{2}}\right)}$

Puente capilar convexo

El caso de los puentes capilares convexos se presenta en la fig. 6, a la izquierda del dominio del caso cilíndrico. ${\textstyle \left({\frac {\pi }{2}}<\theta \leq \pi \right)}$

Estabilidad entre dos superficies planas

Las formas de equilibrio y los límites de estabilidad para los puentes capilares de líquido son objeto de muchos estudios teóricos y experimentales. ^[33] Los estudios se concentran principalmente en la investigación de puentes entre discos iguales en condiciones gravitacionales. Es bien sabido que para cada valor del número de Bond , definido como ^[34] (donde: g es la aceleración gravitacional de la Tierra, γ es la tensión superficial y R es el radio del contacto) el diagrama de estabilidad puede representarse mediante una única curva cerrada por partes en el plano de esbeltez/volumen adimensional. La esbeltez se define como , y el volumen adimensional es el volumen del puente capilar dividido por el volumen del cilindro con la misma altura, H y radio R : . ${\textstyle {\rm {Bo}}={\frac {\rho gR^{2}}{\gamma }}}$ ${\textstyle {\frac {H}{2R}}}$ ${\textstyle {\frac {V}{\pi R^{2}H}}}$

Si tanto la esbeltez como el volumen del líquido son lo suficientemente pequeños, los límites de estabilidad están determinados por el desprendimiento de la forma del líquido de los bordes de los discos (línea de contacto trifásica), línea AB en la figura 7. La línea BC representa el mínimo en volumen que corresponde a la rotura axisimétrica. Se conoce en la literatura como límite mínimo de estabilidad de volumen . La curva CA representa otro límite de estabilidad, que caracteriza el volumen máximo. Es el límite superior de la región de estabilidad. También existe una región de transición entre la estabilidad de volumen mínimo y máximo. Todavía no está claramente definida y, por lo tanto, se indica mediante una línea discontinua en la figura 7. ^{[ ¿ dónde? ]}

Véase también

• Número de Eötvös
• Condensación capilar

Referencias

1. Ross, Sydney (1950). "La inhibición de la formación de espuma. II. Un mecanismo para la ruptura de películas líquidas por agentes antiespumantes". J. Phys. Chem . 54 (3): 429–436. doi :10.1021/j150477a018.
2. Kralchevsky, P.; Nagayama, K. (2001). Partículas en interfases de fluidos y membranas . Ámsterdam: Elsevier. págs. 469–502.
3. Delaunay (1841). "Sur la Surface de Revolution dont la Courbure Moyenne est Constante". J. Matemáticas. Pures Appl . 6 : 309–314.
4. L. Euler, Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, Opera omnia, I, 24, (1744)
5. Kenmotsu, K., Superficies de revolución con curvatura media prescrita, Tohoku Math. J. 32(1980), 147–153.
6. Meseta, Josef (1873). Statique expérimentale et théorique des liquides soumis aux seulesforces moleculares . Gauthier-Villars.
7. Young, T (1805). "Un ensayo sobre la cohesión de fluidos". Philos. Trans. R. Soc. Lond . 95 : 65–87. doi : 10.1098/rstl.1805.0005 .
8. AD Myshkis y VG Babskii, Mecánica de fluidos de baja gravedad: teoría matemática de los fenómenos capilares, Springer-Verlag 1987
9. Nikolai V. Churaev, B. V. Derjaguin, VM Muller, Fuerzas de superficie, Springer Scoence and Business Media, 1987
10. J. Israelashvilly, Fuerzas intermoleculares y de superficie, tercera edición: revisada, Elsevier, 2011
11. Lord Rayleigh (1878). "Sobre la inestabilidad de los chorros". Actas de la London Mathematical Society . 10 : 4–13.
12. Hove, W., Ph.D. Disertación, Friendlich-Wilhelms, Universitat zu Berlin (1887)
13. Meseguer, J.; Sanz, A. (1985). "Estudio numérico y experimental de la dinámica de puentes líquidos axisimétricos". J. Fluid Mech . 153 : 83. doi :10.1017/s002211208500115x (inactivo el 1 de noviembre de 2024).{{cite journal}}: CS1 maint: DOI inactive as of November 2024 (link)
14. Martínez; Perales, JM (1986). "Datos de estabilidad de puentes líquidos". J. Cryst. Growth . 78 (2): 369. Bibcode :1986JCrGr..78..369M. doi :10.1016/0022-0248(86)90073-4.
15. JF Padday, AR Pitt, La estabilidad de los meniscos axisimétricos, Philosophical Transactions of the Royal Society A, (1973)
16. Boucher, EA; Evans, MJB (1975). "Perfiles de gotas colgantes y fenómenos capilares relacionados". Actas de la Royal Society of London A: Ciencias matemáticas y físicas . 346 (1646): 349–374. Bibcode :1975RSPSA.346..349B. doi :10.1098/rspa.1975.0180.
17. Pitts, R., La estabilidad de una gota que cuelga de un tubo, IMA J Appl Math (1976) 17 (3): 387-397
18. Vogel, Thomas I., Estabilidad de una gota de líquido atrapada entre dos planos paralelos, SIAM J. Appl. Math. 47 (1987), 516–525
19. Vogel, Thomas I., Estabilidad de una gota de líquido atrapada entre dos planos paralelos II, SIAM J. Appl. Math. 49 (1989), 1009–1028
20. Michael, DH, Annual Review of Fluid Mechanics Vol. 13: 189-216 (Fecha de publicación del volumen: enero de 1981)
21. Brian James, Lowry; Steen, Paul H. (1995). "Superficies capilares: estabilidad a partir de familias de equilibrios con aplicación al puente líquido". Actas de la Royal Society A . 449 (1937): 411–439. Código Bibliográfico :1995RSPSA.449..411L. doi :10.1098/rspa.1995.0051.
22. A. Fall, B. Weber, M. Pakpour, N. Lenoir, N. Shahidzadeh, J. Fiscina, C. Wagner y D. Bonn, Fricción deslizante en arena húmeda y seca Phys. Rev. Lett. 112, 175502, publicado el 29 de abril de 2014
23. Yumei Men, Xianren Zhang y Wenchuan Wang, Puentes líquidos capilares en microscopía de fuerza atómica (AFM): formación, ruptura e histéresis, J. Chem. Phys. 131, 184702 (2009)
24. Ft. B. EDWARDS, Tolerancias de unión en uniones de tuberías de cobre capilares, Welding Journal, v06, págs. 321-(1972)
25. Persson, BNJ (2007). "Adhesión húmeda con aplicación de adhesivos para almohadillas de dedos y neumáticos de ranas arbóreas". J. Phys.: Condens. Matter . 19 (37): 376110. Bibcode :2007JPCM...19K6110P. doi :10.1088/0953-8984/19/37/376110. S2CID  73607791.
26. Alencar, AM; Majumdar, A.; Hantos, Z.; Buldyrev, SV; Stanley, HE; ​​Suki, B. (2005). "Crujidos e inestabilidades durante la inflación pulmonar". Physica A . 357 : 18–26. Bibcode :2005PhyA..357...18A. doi :10.1016/j.physa.2005.05.047.
27. Pampaloni, F.; Reynaud, EG; Stelzer, EHK (2007). "La tercera dimensión cierra la brecha entre el cultivo celular y el tejido vivo". Nature Reviews Molecular Cell Biology . 8 (10): 839–845. doi :10.1038/nrm2236. PMID  17684528.
28. G. DiLisi, R. Dempsey, R. Rarick y C. Rosenblatt, Uso de vuelos parabólicos para examinar cuantitativamente la estabilidad de puentes líquidos bajo fuerzas corporales totales variables, Sci. and Tech. (enviado)
29. Princen NM, "La forma de equilibrio de las interfaces, gotas y burbujas Partículas rígidas y deformables en las interfaces" en Surface and Colloid Science, ed. E. Matijievich, (1969), v.3, Nueva York
30. Masato Ito, Taku Sato, Observación in situ de un catenoide de película de jabón: un experimento de física educativa simple, Eur. J. Phys. 31 (2010) 357-365
31. Petkov, PV; Radoev, BR (2014). "Estática y dinámica de puentes capilares". Coloides y superficies A. 460 : 18–27. doi :10.1016/j.colsurfa.2014.03.038.
32. Petkov, PV; Radoev, BR (2019). "Investigación de puentes capilares líquidos convexos simples y binarios de tipo "sándwich", estirados entre dos superficies planas (enfoque experimental)". Coloides e interfaces . 3 (68): 68. doi : 10.3390/colloids3040068 .
33. Bezdenejnykh, NA; Meseguer, J.; Perales, JM (1992). "Análisis experimental de los límites de estabilidad de los puentes líquidos capilares". Phys. Fluids A . 4 (4): 677. Bibcode :1992PhFlA...4..677B. doi :10.1063/1.858286.
34. Shi, Z.; et al. (2018). "Histéresis dinámica del ángulo de contacto en puentes líquidos". Coloides y superficies A: aspectos fisicoquímicos y de ingeniería . 555 : 365–371. arXiv : 1712.04703 . doi :10.1016/j.colsurfa.2018.07.004.