Proyección oblicua

Type of technical drawing

Clasificación de la proyección oblicua y algunas proyecciones 3D

La proyección oblicua es un tipo simple de dibujo técnico de proyección gráfica que se utiliza para producir imágenes bidimensionales (2D) de objetos tridimensionales (3D).

Los objetos no están en perspectiva y por lo tanto no corresponden a ninguna vista de un objeto que pueda obtenerse en la práctica, pero la técnica produce resultados bastante convincentes y útiles.

La proyección oblicua se utiliza habitualmente en el dibujo técnico. La proyección caballeresca fue utilizada por los artistas militares franceses en el siglo XVIII para representar fortificaciones.

La proyección oblicua fue utilizada casi universalmente por los artistas chinos desde el siglo I o II hasta el siglo XVIII, especialmente para representar objetos rectilíneos como casas. ^[1]

Se pueden utilizar diversas técnicas de proyección gráfica en gráficos de computadora, incluso en diseño asistido por computadora (CAD), juegos de computadora, animaciones generadas por computadora y efectos especiales utilizados en películas.

Descripción general

Comparación de varios tipos de proyección gráfica . La presencia de uno o más ángulos de 90° en una imagen gráfica suele ser un buen indicio de que la perspectiva es oblicua .

Diversas proyecciones gráficas y cómo se producen

Proyección oblicua de un cubo con escorzo a la mitad, visto de lado

Vista superior de una comparación de una proyección oblicua (izquierda) y una proyección ortográfica (derecha) de un cubo unitario (cian) sobre el plano de proyección (rojo). El factor de escorzo (1/2 en este ejemplo) es inversamente proporcional a la tangente del ángulo (63,43° en este ejemplo) entre el plano de proyección (de color marrón) y las líneas de proyección (punteadas).

Vista frontal del mismo.

La proyección oblicua es un tipo de proyección paralela :

• Proyecta una imagen mediante la intersección de rayos paralelos (proyectores)
• desde el objeto fuente tridimensional con la superficie de dibujo (plano de proyección).

Tanto en la proyección oblicua como en la proyección ortográfica , las líneas paralelas del objeto de origen producen líneas paralelas en la imagen proyectada. Los proyectores en la proyección oblicua intersecan el plano de proyección en un ángulo oblicuo para producir la imagen proyectada, a diferencia del ángulo perpendicular utilizado en la proyección ortográfica.

Matemáticamente, la proyección paralela del punto sobre el plano - da . Las constantes y especifican de forma única una proyección paralela. Cuando , se dice que la proyección es "ortográfica" u "ortogonal". De lo contrario, es "oblicua". Las constantes y no son necesariamente menores que 1 y, como consecuencia, las longitudes medidas en una proyección oblicua pueden ser mayores o menores que en el espacio. En una proyección oblicua general, las esferas del espacio se proyectan como elipses en el plano de dibujo y no como círculos, como aparecerían en una proyección ortogonal. ${\displaystyle (x,y,z)}$ ${\displaystyle xy}$ ${\displaystyle (x+az,y+bz,0)}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a=b=0}$ ${\displaystyle a}$ ${\displaystyle b}$

El dibujo oblicuo es también el método de dibujo "3D" más rudimentario, pero el más fácil de dominar. Una forma de dibujar usando una vista oblicua es dibujar el lado del objeto que se está mirando en dos dimensiones, es decir, plano, y luego dibujar los otros lados en un ángulo de 45°, pero en lugar de dibujar los lados a tamaño completo, solo se dibujan con la mitad de la profundidad, creando una "profundidad forzada", que agrega un elemento de realismo al objeto. Incluso con esta "profundidad forzada", los dibujos oblicuos se ven muy poco convincentes a la vista. Por esta razón, los diseñadores o ingenieros profesionales rara vez utilizan el dibujo oblicuo.

Imagen oblicua

En un dibujo pictórico oblicuo , los ángulos representados entre los ejes, así como los factores de escorzo (escala) son arbitrarios. Más precisamente, cualquier conjunto dado de tres segmentos coplanares que se originan en el mismo punto puede interpretarse como si formaran una perspectiva oblicua de tres lados de un cubo. Este resultado se conoce como el teorema de Pohlke , del matemático alemán Pohlke, quien lo publicó a principios del siglo XIX. ^[2]

Las distorsiones resultantes hacen que la técnica no sea adecuada para dibujos formales y de trabajo. Sin embargo, las distorsiones se superan parcialmente alineando un plano de la imagen paralelo al plano de proyección. Al hacerlo, se crea una imagen de forma real del plano elegido. Esta categoría específica de proyecciones oblicuas, en las que se conservan las longitudes a lo largo de las direcciones y , pero las longitudes a lo largo de la dirección se dibujan en ángulo utilizando un factor de reducción, se utiliza mucho en dibujos industriales. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$

• La proyección caballera es el nombre de este tipo de proyección, donde la longitud a lo largo del eje permanece sin escala. ^[3] ${\displaystyle z}$
• La proyección de gabinete , popular en las ilustraciones de muebles, es un ejemplo de tal técnica, donde el eje que retrocede se escala a la mitad del tamaño ^[3] (a veces en lugar de dos tercios del original). ^[4]

Proyección de caballero

En la proyección caballera (a veces perspectiva caballera o punto de vista elevado ) un punto del objeto se representa mediante tres coordenadas, x , y y z . En el dibujo, se representa mediante solo dos coordenadas, x″ e y″ . En el dibujo plano, dos ejes, x y z en la figura, son perpendiculares y la longitud de estos ejes se dibuja con una escala 1:1; por lo tanto, es similar a las proyecciones dimétricas , aunque no es una proyección axonométrica , ya que el tercer eje, aquí y , se dibuja en diagonal, formando un ángulo arbitrario con el eje x″ , generalmente 30 o 45°. La longitud del tercer eje no está escalada. ^{[5] [6]}

Es muy fácil de dibujar, especialmente con lápiz y papel, por lo que se utiliza a menudo cuando se debe dibujar una figura a mano, por ejemplo en una pizarra (clase, examen oral).

La representación se utilizó inicialmente para fortificaciones militares . En francés, el "caballero" (literalmente jinete, véase Caballería ) es una colina artificial detrás de las murallas que permite avistar al enemigo por encima de las murallas. ^[7] La ​​perspectiva del caballero era la forma en que se veían las cosas desde este punto alto. Algunos también explican el nombre por el hecho de que era la forma en que un jinete podía ver un objeto pequeño en el suelo desde su caballo. ^[8]

Proyección del gabinete

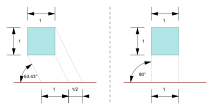
El término proyección de gabinete proviene de su uso en ilustraciones de la industria del mueble. ^[9] Al igual que en la perspectiva caballeresca, una cara del objeto proyectado es paralela al plano de visualización y el tercer eje se proyecta como si se alejara en un ángulo (normalmente atan(2) o aproximadamente ~63,4°). A diferencia de la proyección caballeresca, donde el tercer eje mantiene su longitud, con la proyección de gabinete la longitud de las líneas que se alejan se reduce a la mitad.

Fórmula matemática

Como fórmula, si el plano que mira hacia el espectador es xy y el eje que retrocede es z , entonces un punto P se proyecta de esta manera:

${\displaystyle P{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}x+{\frac {1}{2}}z\cos \alpha \\y+{\frac {1}{2}}z\sin \alpha \\0\end{pmatrix}}}$

¿Dónde está el ángulo mencionado? ${\displaystyle \alpha }$

La matriz de transformación es:

${\displaystyle P={\begin{bmatrix}1&0&{\frac {1}{2}}\cos \alpha \\0&1&{\frac {1}{2}}\sin \alpha \\0&0&0\end{bmatrix}}}$

Alternativamente, se podría quitar un tercio del brazo principal que sobresale de la cara de partida, obteniendo así el mismo resultado.

Proyección militar

En la proyección militar , los ángulos de los ejes x y z y de los ejes y y z son de 45°, lo que significa que el ángulo entre el eje x y el eje y es de 90°. Es decir, el plano xy no está sesgado, sino que está rotado 45°. ^[10]

Ejemplos

Además de los dibujos técnicos y las ilustraciones, los videojuegos (sobre todo los anteriores a la aparición de los juegos en 3D) también suelen utilizar algún tipo de proyección oblicua. Algunos ejemplos son SimCity , Ultima VII , Ultima Online , EarthBound , Paperboy y, más recientemente, Tibia .

• 
  Las figuras de la izquierda son proyecciones ortográficas . La figura de la derecha es una proyección oblicua con un ángulo de 30° y una razón de 1 ⁄ 2 .
• 
  Banco de macetas dibujado en proyección de gabinete con un ángulo de 45° y una relación de 2/3.
• 
  Piezas de fortificación en perspectiva caballeresca ( Ciclopedia vol. 1, 1728).
• 
  Cómo se utilizan las coordenadas para colocar un punto en una perspectiva caballera .
• Arco de piedra dibujado en perspectiva militar .
• 
  Arco de piedra dibujado en perspectiva de gabinete .
• 
  Una pintura representativa coreana que representa los dos palacios reales, Changdeokgung y Changgyeonggung, ubicados al este del palacio principal, Gyeongbokgung .
• 
  Entrada y patio de un yamen . Detalle de un pergamino sobre Suzhou realizado por Xu Yang, encargado por el emperador Qianlong . Siglo XVIII
• 
  Plano del siglo XVIII de Port-Royal-des-Champs dibujado en proyección militar
• 
  En el videojuego SimCity se utiliza una variación de la proyección militar.
• 
  Angiografía por resonancia magnética en 3D , mostrada en proyección oblicua para distinguir la arteria subclavia aberrante.

Véase también

• Proyección de Mercator oblicua al espacio
• Proyección oblicua de Mercator
• Hatsusaburō Yoshida
• Lista de técnicas artísticas

Referencias

1. Cucker, Felipe (2013). Espejos múltiples: el cruce de caminos entre las artes y las matemáticas . Cambridge University Press. pp. 269–278. ISBN 978-0-521-72876-8.
2. Weisstein, Eric W. "Teorema de Pohlke". De MathWorld—Un recurso web de Wolfram.
3. Proyecciones paralelas Archivado el 23 de abril de 2007 en Wayback Machine desde PlaneView3D Online
4. Bolton, William (1995), Ingeniería básica , Butterworth-Heinemann GNVQ Engineering Series, BH Newnes, pág. 140, ISBN 9780750625845.
5. "Manuales de reparación y mantenimiento - Publicaciones integradas". Archivado desde el original el 22 de agosto de 2010 . Consultado el 22 de agosto de 2010 .de "Manuales de reparación y mantenimiento - Publicaciones integradas". Archivado desde el original el 22 de agosto de 2010 . Consultado el 22 de agosto de 2010 .
6. Ingrid Carlbom, Joseph Paciorek, Proyecciones geométricas planas y transformaciones de visualización, ACM Computing Surveys , v.10 n.4, págs. 465–502, diciembre de 1978
7. Etimología de las matemáticas, letra C (francés)
8. DES QUESTIONS D'ORIGINES (francés)
9. Ching, Francis DK; Juroszek, Steven P. (2011), Dibujo de diseño (2.ª ed.), John Wiley & Sons, pág. 205, ISBN 9781118007372.
10. "La geometría del dibujo en perspectiva en el ordenador" . Consultado el 24 de abril de 2015 .

Lectura adicional

• Foley, James (1997). Gráficos por ordenador . Boston: Addison-Wesley. ISBN 0-201-84840-6.
• Ingrid Carlbom, Joseph Paciorek, Proyecciones geométricas planas y transformaciones de visualización, ACM Computing Surveys , v.10 n.4, p. 465–502, diciembre de 1978
• Alpha et al. 1988, Atlas de mapas oblicuos, una colección de representaciones de relieves de áreas seleccionadas del mundo ( Servicio Geológico de Estados Unidos )

Enlaces externos

• Illustrator Draftsman 3 y 2: volumen 2, prácticas estándar y teoría, página 68 de https://web.archive.org/web/20100822152816/http://www.tpub.com:80/