El dilema del prisionero

Ejemplo estándar en teoría de juegos

El dilema del prisionero es un experimento mental de teoría de juegos que involucra a dos agentes racionales , cada uno de los cuales puede cooperar para beneficio mutuo o traicionar a su compañero ("desertar") para obtener una ganancia individual. El dilema surge del hecho de que, si bien desertar es racional para cada agente, la cooperación produce una recompensa mayor para cada uno. El rompecabezas fue diseñado por Merrill Flood y Melvin Dresher en 1950 durante su trabajo en la Corporación RAND . ^[1] Invitaron al economista Armen Alchian y al matemático John Williams a jugar cien rondas del juego, observando que Alchian y Williams a menudo optaban por cooperar. Cuando se le preguntó sobre los resultados, John Nash señaló que el comportamiento racional en la versión iterada del juego puede diferir del de una versión de una sola ronda. Esta idea anticipó un resultado clave en la teoría de juegos : la cooperación puede surgir en interacciones repetidas, incluso en situaciones en las que no es racional en una interacción única.

Albert W. Tucker denominó más tarde al juego "dilema del prisionero" al enmarcar las recompensas en términos de sentencias de prisión. ^[2] El dilema del prisionero modela muchas situaciones del mundo real que implican un comportamiento estratégico. En el uso informal, la etiqueta "dilema del prisionero" se aplica a cualquier situación en la que dos entidades pueden obtener beneficios importantes al cooperar o sufrir al no hacerlo, pero les resulta difícil o costoso coordinar sus elecciones.

Premisa

Un ejemplo de matriz de resultados del dilema del prisionero

William Poundstone describió esta "versión contemporánea típica" del juego en su libro de 1993 El dilema del prisionero :

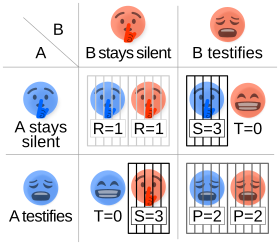
Dos miembros de una banda criminal son arrestados y encarcelados. Cada prisionero está en confinamiento solitario sin medios para hablar o intercambiar mensajes con el otro. La policía admite que no tiene pruebas suficientes para condenar a la pareja por el cargo principal. Planean condenar a ambos a un año de prisión por un cargo menor. Al mismo tiempo, la policía ofrece a cada prisionero un trato fáustico : si testifica contra su compañero, quedará libre, mientras que el compañero será condenado a tres años de prisión por el cargo principal. Ah, sí, hay una trampa... Si ambos prisioneros testifican uno contra el otro, ambos serán condenados a dos años de prisión. Los prisioneros tienen un poco de tiempo para pensarlo, pero en ningún caso pueden saber lo que el otro ha decidido hasta que haya tomado su decisión irrevocablemente. A cada uno se le informa de que al otro prisionero se le ofrece exactamente el mismo trato. Cada prisionero está preocupado sólo por su propio bienestar: minimizar su propia sentencia de prisión. ^[3]

Esto conduce a cuatro posibles resultados diferentes para los prisioneros A y B:

1. Si A y B permanecen en silencio, cada uno cumplirá un año de prisión.
2. Si A testifica contra B pero B permanece en silencio, A quedará libre mientras B cumplirá tres años de prisión.
3. Si A permanece en silencio pero B testifica contra A, A cumplirá tres años de prisión y B quedará en libertad.
4. Si A y B testifican uno contra el otro, cada uno cumplirá dos años de cárcel.

Estrategia para el dilema del prisionero

Dos prisioneros están separados en habitaciones individuales y no pueden comunicarse entre sí. Se supone que ambos prisioneros comprenden la naturaleza del juego, no tienen lealtad entre sí y no tendrán oportunidad de recibir retribución o recompensa fuera del juego. El juego normal se muestra a continuación: ^[4]

Independientemente de lo que decida el otro, cada prisionero obtiene una recompensa mayor por traicionar al otro ("desertar"). El razonamiento implica analizar las mejores respuestas de ambos jugadores : B cooperará o desertará. Si B coopera, A debería desertar, porque quedar libre es mejor que cumplir 1 año. Si B deserta, A también debería desertar, porque cumplir 2 años es mejor que cumplir 3. Por lo tanto, en cualquier caso, A debería desertar, ya que desertar es la mejor respuesta de A, independientemente de la estrategia de B. El razonamiento paralelo mostrará que B debería desertar.

La deserción siempre produce mejores resultados que la cooperación, por lo que es una estrategia estrictamente dominante para ambos jugadores. La deserción mutua es el único equilibrio de Nash sólido en el juego. Dado que el resultado ideal colectivo de la cooperación mutua es irracional desde un punto de vista egoísta, este equilibrio de Nash no es eficiente en el sentido de Pareto .

Forma generalizada

La estructura del dilema del prisionero tradicional se puede generalizar a partir de su escenario original. Supongamos que los dos jugadores están representados por los colores rojo y azul y que cada jugador elige "cooperar" o "desertar".

Si ambos jugadores cooperan, ambos reciben la recompensa por cooperar. Si ambos jugadores desertan, ambos reciben el castigo . Si Azul deserta mientras Rojo coopera, entonces Azul recibe el pago de la tentación , mientras que Rojo recibe el pago del "incauto", . De manera similar, si Azul coopera mientras Rojo deserta, entonces Azul recibe el pago del incauto , mientras que Rojo recibe el pago de la tentación . ${\displaystyle R}$ ${\displaystyle P}$ ${\displaystyle T}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle T}$

Esto se puede expresar en forma normal :

y para ser un juego de dilema del prisionero en el sentido estricto, la siguiente condición debe cumplirse para los pagos:

⁠ ⁠ ${\displaystyle T>R>P>S}$

La relación de pago ⁠ ⁠ ${\displaystyle R>P}$ implica que la cooperación mutua es superior a la deserción mutua, mientras que las relaciones de pago ⁠ ⁠ ${\displaystyle T>R}$ y ⁠ ⁠ ${\displaystyle P>S}$ implican que la deserción es la estrategia dominante para ambos agentes.

El dilema del prisionero reiterado

Si dos jugadores juegan el dilema del prisionero más de una vez seguidas, recuerdan las acciones anteriores de su oponente y se les permite cambiar su estrategia en consecuencia, el juego se denomina dilema del prisionero iterado.

Además de la forma general anterior, la versión iterativa también requiere que ⁠ ⁠ ${\displaystyle 2R>T+S}$ , para evitar que la cooperación y la deserción alternadas den una recompensa mayor que la cooperación mutua.

El dilema del prisionero iterado es fundamental para algunas teorías de la cooperación y la confianza humanas. Suponiendo que el juego modela eficazmente las transacciones entre dos personas que requieren confianza, el comportamiento cooperativo en las poblaciones puede modelarse mediante una versión iterada del juego para varios jugadores. En 1975, Grofman y Pool calcularon que el número de artículos académicos dedicados al dilema del prisionero iterado era superior a 2.000. El dilema del prisionero iterado también se denomina " juego de paz-guerra ". ^{[5] [6]}

Estrategia general

Si el dilema del prisionero iterado se juega un número finito de veces y ambos jugadores lo saben, entonces la estrategia dominante y el equilibrio de Nash es desertar en todas las rondas. La prueba es inductiva : uno podría desertar en el último turno, ya que el oponente no tendrá la oportunidad de tomar represalias más tarde. Por lo tanto, ambos desertarán en el último turno. Por lo tanto, el jugador también podría desertar en el penúltimo turno, ya que el oponente desertará en el último sin importar lo que haga, y así sucesivamente. Lo mismo se aplica si la duración del juego es desconocida pero tiene un límite superior conocido. ^{[ cita requerida ]}

Para que se produzca una cooperación entre jugadores racionales, el número de rondas debe ser desconocido o infinito. En ese caso, la estrategia de “siempre desertar” puede dejar de ser dominante. Como demostró Robert Aumann en un artículo de 1959 ^[7] , los jugadores racionales que interactúan repetidamente durante partidas indefinidamente largas pueden mantener la cooperación. En concreto, un jugador puede estar menos dispuesto a cooperar si su contraparte no cooperó muchas veces, lo que provoca decepción. Por el contrario, a medida que transcurre el tiempo, la probabilidad de cooperación tiende a aumentar, debido al establecimiento de un “acuerdo tácito” entre los jugadores participantes. En situaciones experimentales, la cooperación puede darse incluso cuando ambos participantes saben cuántas iteraciones se jugarán. ^[8]

Según un estudio experimental de 2019 publicado en la revista American Economic Review , que puso a prueba las estrategias que utilizaban los sujetos de la vida real en situaciones iteradas del dilema del prisionero con un seguimiento perfecto, la mayoría de las estrategias elegidas siempre fueron desertar, tit-for-tat y grim trigger . La estrategia que eligieron los sujetos dependía de los parámetros del juego. ^[9]

Condiciones de estrategia exitosas y torneo de Axelrod

El interés por el dilema del prisionero iterado fue despertado por Robert Axelrod en su libro de 1984 The Evolution of Cooperation (La evolución de la cooperación) , en el que informa sobre un torneo que organizó sobre el dilema del prisionero de N pasos (con N fijo) en el que los participantes tienen que elegir su estrategia repetidamente y recordar sus encuentros anteriores. Axelrod invitó a colegas académicos de todo el mundo a idear estrategias informáticas para competir en un torneo de dilema del prisionero iterado. Los programas que participaron variaban ampliamente en complejidad algorítmica, hostilidad inicial, capacidad de perdón, etc.

Axelrod descubrió que cuando estos encuentros se repetían durante un largo período de tiempo con muchos jugadores, cada uno con estrategias diferentes, las estrategias codiciosas tendían a tener un rendimiento muy deficiente a largo plazo, mientras que las estrategias más altruistas obtenían mejores resultados, a juzgar únicamente por el interés propio. Utilizó esto para demostrar un posible mecanismo para la evolución del comportamiento altruista a partir de mecanismos que inicialmente son puramente egoístas, por selección natural .

La estrategia determinista ganadora fue tit for tat , desarrollada y presentada en el torneo por Anatol Rapoport . Fue el programa más simple de todos los presentados, con solo cuatro líneas de BASIC , ^[10] y ganó el concurso. La estrategia es simplemente cooperar en la primera iteración del juego; después de eso, el jugador hace lo que hizo su oponente en el movimiento anterior. ^[11] Dependiendo de la situación, una estrategia ligeramente mejor puede ser "tit for tat con perdón": cuando el oponente deserta, en el siguiente movimiento, el jugador a veces coopera de todos modos, con una pequeña probabilidad (alrededor del 1-5%, dependiendo de la alineación de oponentes). Esto permite una recuperación ocasional de quedar atrapado en un ciclo de deserciones.

Después de analizar las estrategias con mayor puntuación, Axelrod enunció varias condiciones necesarias para que una estrategia tenga éxito: ^[12]

• Agradable : La estrategia no será la primera en fallar (a esto a veces se lo llama algoritmo "optimista" ^{[¿ quién lo llama? ]} ), es decir, no "engañará" a su oponente por razones puramente egoístas primero. Casi todas las estrategias con mejores puntajes fueron agradables. ^[a]
• Tomar represalias : la estrategia debe tomar represalias en ocasiones. Un ejemplo de una estrategia sin represalias es Cooperar siempre, una muy mala opción que con frecuencia será explotada por estrategias "malas".
• Perdonador : las estrategias exitosas deben ser indulgentes. Aunque los jugadores tomarán represalias, volverán a cooperar si el oponente no continúa desertando. Esto puede detener largas rachas de venganza y contravenganza, maximizando los puntos. ^[b]
• Sin envidia : La estrategia no debe esforzarse en anotar más que el oponente.

A diferencia del dilema del prisionero que se juega una sola vez, la estrategia óptima en el dilema del prisionero iterado depende de las estrategias de los oponentes probables y de cómo reaccionarán a las deserciones y la cooperación. Por ejemplo, si una población está formada exclusivamente por jugadores que siempre desertan, excepto uno que sigue la estrategia de ojo por ojo, esa persona está en ligera desventaja debido a la derrota en el primer turno. En una población así, la estrategia óptima es desertar siempre. En términos más generales, dada una población con un cierto porcentaje de desertores constantes y el resto de jugadores que siguen la estrategia de ojo por ojo, la estrategia óptima depende del porcentaje y la cantidad de iteraciones jugadas. ^{[ cita requerida ]}

Otras estrategias

La derivación de la estrategia óptima generalmente se realiza de dos maneras:

• Equilibrio de Nash bayesiano : si se puede determinar la distribución estadística de las estrategias opuestas, se puede derivar analíticamente una contraestrategia óptima. ^[c]
• Se han realizado simulaciones de poblaciones con el método Monte Carlo , en las que los individuos con puntuaciones bajas mueren y los que tienen puntuaciones altas se reproducen (un algoritmo genético para encontrar una estrategia óptima). La combinación de algoritmos en la población final depende generalmente de la combinación en la población inicial. La introducción de mutaciones (variación aleatoria durante la reproducción) reduce la dependencia de la población inicial; los experimentos empíricos con tales sistemas tienden a producir jugadores que se benefician mutuamente ^{[ aclaración necesaria ]} , pero no existe ninguna prueba analítica de que esto siempre ocurrirá. ^[16]

En la estrategia llamada ganar-quedarse, perder-cambiar , ante una falta de cooperación, el jugador cambia de estrategia en el siguiente turno. ^[17] En determinadas circunstancias, ^{[ especificar ]} Pavlov supera a todas las demás estrategias al dar un trato preferencial a los jugadores que utilizan una estrategia similar.

Aunque el tit-for-tat se considera la estrategia básica más sólida , un equipo de la Universidad de Southampton en Inglaterra introdujo una estrategia más exitosa en la competencia iterada del dilema del prisionero del 20 aniversario. Se basó en la colusión entre programas para lograr la mayor cantidad de puntos para un solo programa. La universidad presentó 60 programas a la competencia, que fueron diseñados para reconocerse entre sí a través de una serie de cinco a diez movimientos al comienzo. ^[18] Una vez que se hizo este reconocimiento, un programa siempre cooperaría y el otro siempre desertaría, asegurando la cantidad máxima de puntos para el desertor. Si el programa se daba cuenta de que estaba jugando con un jugador que no era de Southampton, desertaría continuamente en un intento de minimizar la puntuación del programa competidor. Como resultado, los resultados del Torneo del Dilema del Prisionero de 2004 muestran las estrategias de la Universidad de Southampton en los primeros tres lugares (y una serie de posiciones hacia el final), a pesar de tener menos victorias y muchas más derrotas que la estrategia GRIM. La estrategia de Southampton aprovecha el hecho de que se permitían múltiples inscripciones en esta competición en particular y que el rendimiento de un equipo se medía por el del jugador con mayor puntuación (lo que significa que el uso de jugadores abnegados era una forma de minmaxing ).

Debido a esta nueva regla, esta competencia también tiene poca importancia teórica al analizar estrategias de un solo agente en comparación con el torneo seminal de Axelrod. Pero proporcionó una base para analizar cómo lograr estrategias cooperativas en marcos de múltiples agentes, especialmente en presencia de ruido.

Mucho antes de que se jugara este torneo con nuevas reglas, Dawkins, en su libro El gen egoísta , señaló la posibilidad de que esas estrategias ganaran si se permitían múltiples participantes, pero remarcó que Axelrod probablemente no las hubiera permitido si se hubieran presentado. También se basa en eludir la regla de que no se permite la comunicación entre jugadores, lo que los programas de Southampton probablemente hicieron con su "baile de diez movimientos" preprogramado para reconocerse entre sí, lo que refuerza lo valiosa que puede ser la comunicación para cambiar el equilibrio del juego.

Incluso sin una colusión implícita entre las estrategias de software , el tit-for-tat no siempre es el ganador absoluto de un torneo determinado; más precisamente, sus resultados a largo plazo en una serie de torneos superan a sus rivales, pero esto no significa que sea el más exitoso en el corto plazo. Lo mismo se aplica al tit-for-tat con perdón y otras estrategias óptimas.

Esto también se puede ilustrar utilizando la simulación darwiniana de la ESS . En una simulación de este tipo, el sistema de represalias casi siempre acabará dominando, aunque las estrategias maliciosas irán entrando y saliendo de la población porque una población de represalias es penetrable por las estrategias amables que no toman represalias, que a su vez son presa fácil de las estrategias maliciosas. Dawkins demostró que aquí ninguna combinación estática de estrategias forma un equilibrio estable y el sistema siempre oscilará entre límites. ^{[ cita requerida ]}

Dilema del prisionero iterado estocástico

En un juego iterado estocástico de dilema del prisionero, las estrategias se especifican en términos de "probabilidades de cooperación". ^[19] En un encuentro entre el jugador X y el jugador Y , la estrategia de X se especifica mediante un conjunto de probabilidades P de cooperar con Y. P es una función de los resultados de sus encuentros anteriores o algún subconjunto de los mismos. Si P es una función solo de sus n encuentros más recientes , se denomina estrategia de "memoria-n". Una estrategia de memoria-1 se especifica entonces mediante cuatro probabilidades de cooperación: , donde P _cd es la probabilidad de que X coopere en el encuentro actual dado que el encuentro anterior se caracterizó por la cooperación de X y la deserción de Y. Si cada una de las probabilidades es 1 o 0, la estrategia se denomina determinista. Un ejemplo de una estrategia determinista es la estrategia tit-for-tat escrita como , en la que X responde como lo hizo Y en el encuentro anterior. Otra es la estrategia de cambio de ganar-quedarse, perder escrita como . Se ha demostrado que para cualquier estrategia de memoria-n existe una estrategia de memoria-1 correspondiente que da los mismos resultados estadísticos, de modo que solo es necesario considerar las estrategias de memoria-1. ^[19] ${\displaystyle P=\{P_{cc},P_{cd},P_{dc},P_{dd}\}}$ ${\displaystyle P=\{1,0,1,0\}}$ ${\displaystyle P=\{1,0,0,1\}}$

Si se define como el vector de estrategia de 4 elementos anterior de X y como el vector de estrategia de 4 elementos de Y (donde los índices son desde el punto de vista de Y ), se puede definir una matriz de transición M para X cuya entrada ij -ésima es la probabilidad de que el resultado de un encuentro particular entre X e Y sea j dado que el encuentro anterior fue i , donde i y j son uno de los cuatro índices de resultado: cc , cd , dc o dd . Por ejemplo, desde el punto de vista de X , la probabilidad de que el resultado del encuentro actual sea cd dado que el encuentro anterior fue cd es igual a . Según estas definiciones, el dilema del prisionero iterado califica como un proceso estocástico y M es una matriz estocástica , lo que permite aplicar toda la teoría de los procesos estocásticos. ^[19] ${\displaystyle P}$ ${\displaystyle Q=\{Q_{cc},Q_{cd},Q_{dc},Q_{dd}\}}$ ${\displaystyle M_{cd,cd}=P_{cd}(1-Q_{dc})}$

Un resultado de la teoría estocástica es que existe un vector estacionario v para la matriz v tal que . Sin pérdida de generalidad, se puede especificar que v está normalizado de modo que la suma de sus cuatro componentes es la unidad. La entrada ij -ésima en dará la probabilidad de que el resultado de un encuentro entre X e Y sea j dado que el encuentro n pasos anterior es i . En el límite, cuando n se acerca al infinito, M convergerá a una matriz con valores fijos, dando las probabilidades a largo plazo de un encuentro que produzca j independientemente de i . En otras palabras, las filas de serán idénticas, dando las probabilidades del resultado de equilibrio a largo plazo del dilema del prisionero iterado sin la necesidad de evaluar explícitamente un gran número de interacciones. Se puede ver que v es un vector estacionario para y particularmente , de modo que cada fila de será igual a v . Por lo tanto, el vector estacionario especifica las probabilidades del resultado de equilibrio para X . Al definir y como los vectores de pagos a corto plazo para los resultados { cc,cd,dc,dd } (desde el punto de vista de X ), los pagos de equilibrio para X e Y ahora se pueden especificar como y , lo que permite comparar las dos estrategias P y Q para sus pagos a largo plazo. ${\displaystyle v\cdot M=v}$ ${\displaystyle M^{n}}$ ${\displaystyle M^{\infty }}$ ${\displaystyle M^{n}}$ ${\displaystyle M^{\infty }}$ ${\displaystyle M^{\infty }}$ ${\displaystyle S_{x}=\{R,S,T,P\}}$ ${\displaystyle S_{y}=\{R,T,S,P\}}$ ${\displaystyle s_{x}=v\cdot S_{x}}$ ${\displaystyle s_{y}=v\cdot S_{y}}$

Estrategias de determinante cero

Relación entre las estrategias de determinante cero (ZD), de cooperación y de deserción en el dilema del prisionero iterado (dilema del prisionero iterado)

En 2012, William H. Press y Freeman Dyson publicaron una nueva clase de estrategias para el dilema del prisionero iterado estocástico llamadas estrategias de "determinante cero" (ZD). ^[19] Los pagos a largo plazo para los encuentros entre X e Y se pueden expresar como el determinante de una matriz que es una función de las dos estrategias y los vectores de pago a corto plazo: y , que no involucran al vector estacionario v . Dado que la función determinante es lineal en , se deduce que (donde ). Cualquier estrategia para la cual es por definición una estrategia ZD, y los pagos a largo plazo obedecen a la relación . ${\displaystyle s_{x}=D(P,Q,S_{x})}$ ${\displaystyle s_{y}=D(P,Q,S_{y})}$ ${\displaystyle s_{y}=D(P,Q,f)}$ ${\displaystyle f}$ ${\displaystyle \alpha s_{x}+\beta s_{y}+\gamma =D(P,Q,\alpha S_{x}+\beta S_{y}+\gamma U)}$ ${\displaystyle U=\{1,1,1,1\}}$ ${\displaystyle D(P,Q,\alpha S_{x}+\beta S_{y}+\gamma U)=0}$ ${\displaystyle \alpha s_{x}+\beta s_{y}+\gamma =0}$

El juego de ojo por ojo es una estrategia de ZD que es "justa", en el sentido de no obtener ventaja sobre el otro jugador. Pero el espacio de ZD también contiene estrategias que, en el caso de dos jugadores, pueden permitir a un jugador fijar unilateralmente la puntuación del otro jugador o, alternativamente, forzar a un jugador evolutivo a lograr una recompensa un porcentaje menor que la suya. El jugador extorsionado podría desertar, pero se perjudicaría a sí mismo al obtener una recompensa menor. Por lo tanto, las soluciones de extorsión convierten el dilema del prisionero iterado en una especie de juego de ultimátum . Específicamente, X puede elegir una estrategia para la cual , fijando unilateralmente s _y en un valor específico dentro de un rango particular de valores, independientemente de la estrategia de Y , ofreciendo una oportunidad para que X "extorsione" al jugador Y (y viceversa). Pero si X intenta fijar s _x en un valor particular, el rango de posibilidades es mucho más pequeño, y consiste solo en cooperación completa o deserción completa. ^[19] ${\displaystyle D(P,Q,\beta S_{y}+\gamma U)=0}$

Una extensión del dilema del prisionero iterado es un dilema del prisionero iterado estocástico evolutivo, en el que se permite que la abundancia relativa de estrategias particulares cambie, y las estrategias más exitosas aumenten relativamente. Este proceso se puede lograr haciendo que los jugadores menos exitosos imiten las estrategias más exitosas, o eliminando a los jugadores menos exitosos del juego, mientras se multiplican los más exitosos. Se ha demostrado que las estrategias ZD injustas no son evolutivamente estables . La intuición clave es que una estrategia evolutivamente estable no solo debe ser capaz de invadir otra población (lo que pueden hacer las estrategias ZD extorsivas), sino que también debe funcionar bien contra otros jugadores del mismo tipo (lo que los jugadores ZD extorsivos hacen mal porque reducen el excedente de los demás). ^[20]

La teoría y las simulaciones confirman que, más allá de un tamaño crítico de población, la extorsión ZD pierde en la competencia evolutiva frente a estrategias más cooperativas y, como resultado, la recompensa promedio en la población aumenta cuando la población es mayor. Además, hay algunos casos en los que los extorsionadores pueden incluso catalizar la cooperación ayudando a salir de un enfrentamiento entre desertores uniformes y agentes que ganan-se quedan, pierden-cambian . ^[21]

Si bien las estrategias ZD extorsivas no son estables en poblaciones grandes, otra clase de ZD llamada estrategias "generosas" es estable y robusta. Cuando la población no es demasiado pequeña, estas estrategias pueden suplantar a cualquier otra estrategia ZD e incluso funcionar bien contra una amplia gama de estrategias genéricas para el dilema del prisionero iterado, incluyendo ganar-quedarse, perder-cambiar. Esto fue probado específicamente para el juego de donación por Alexander Stewart y Joshua Plotkin en 2013. ^[22] Las estrategias generosas cooperarán con otros jugadores cooperativos, y ante la deserción, el jugador generoso pierde más utilidad que su rival. Las estrategias generosas son la intersección de las estrategias ZD y las llamadas estrategias "buenas", que fueron definidas por Ethan Akin como aquellas para las cuales el jugador responde a la cooperación mutua pasada con cooperación futura y divide los pagos esperados equitativamente si recibe al menos el pago esperado cooperativo. ^[23] Entre las buenas estrategias, el subconjunto generoso (ZD) funciona bien cuando la población no es demasiado pequeña. Si la población es muy pequeña, las estrategias de deserción tienden a dominar. ^[22]

Dilema del prisionero iterado continuo

La mayor parte de los trabajos sobre el dilema del prisionero iterado se han centrado en el caso discreto, en el que los jugadores cooperan o desertan, porque este modelo es relativamente sencillo de analizar. Sin embargo, algunos investigadores han estudiado modelos del dilema del prisionero iterado continuo, en el que los jugadores pueden hacer una contribución variable al otro jugador. Le y Boyd ^[24] descubrieron que en tales situaciones, la cooperación es mucho más difícil de desarrollar que en el dilema del prisionero iterado discreto. En un dilema del prisionero continuo, si una población comienza en un equilibrio no cooperativo, los jugadores que son sólo marginalmente más cooperativos que los no cooperadores obtienen poco beneficio de la selección entre ellos. Por el contrario, en un dilema del prisionero discreto, los cooperadores ojo por ojo obtienen un gran aumento de recompensa por la selección entre ellos en un equilibrio no cooperativo, en relación con los no cooperadores. Dado que se podría decir que la naturaleza ofrece más oportunidades para una cooperación variable que una dicotomía estricta de cooperación o deserción, el dilema del prisionero continuo puede ayudar a explicar por qué los ejemplos de la vida real de cooperación tipo "ojo por ojo" son extremadamente raros ^[25], aunque el "ojo por ojo" parece sólido en los modelos teóricos.

Ejemplos de la vida real

Muchos casos de interacción humana y procesos naturales tienen matrices de resultados como la del dilema del prisionero. Por lo tanto, es de interés para las ciencias sociales , como la economía , la política y la sociología , así como para las ciencias biológicas, como la etología y la biología evolutiva . Muchos procesos naturales se han abstraído en modelos en los que los seres vivos participan en juegos interminables de dilema del prisionero.

Estudios ambientales

En los estudios ambientales , el dilema es evidente en crisis como el cambio climático global . Se sostiene que todos los países se beneficiarán de un clima estable, pero cualquier país por sí solo suele ser reticente a reducir las emisiones de CO2 . Se considera que el beneficio inmediato que obtendría cualquier país si mantuviera su comportamiento actual es mayor que el supuesto beneficio final que obtendría ese país si cambiara el comportamiento de todos los países, lo que explica el impasse en torno al cambio climático en 2007. ^[26]

Una diferencia importante entre la política del cambio climático y el dilema del prisionero es la incertidumbre: no se sabe en qué medida y a qué ritmo la contaminación puede cambiar el clima. Por lo tanto, el dilema al que se enfrentan los gobiernos es diferente del dilema del prisionero en que se desconocen los beneficios de la cooperación. Esta diferencia sugiere que los Estados cooperarán mucho menos que en un dilema del prisionero iterado real, de modo que la probabilidad de evitar una posible catástrofe climática es mucho menor que la sugerida por un análisis de la situación basado en la teoría de juegos utilizando un dilema del prisionero iterado real. ^[27]

Thomas Osang y Arundhati Nandy ofrecen una explicación teórica con pruebas para una situación de beneficio mutuo impulsada por la regulación, en la línea de la hipótesis de Michael Porter , en la que la regulación gubernamental de las empresas competidoras es sustancial. ^[28]

Animales

La conducta cooperativa de muchos animales puede entenderse como un ejemplo del dilema del prisionero iterado. A menudo, los animales establecen asociaciones a largo plazo; por ejemplo, los guppies inspeccionan a los depredadores de manera cooperativa en grupos y se cree que castigan a los inspectores que no cooperan. ^[29]

Los murciélagos vampiros son animales sociales que intercambian alimentos de forma recíproca. La aplicación de los resultados del dilema del prisionero puede ayudar a explicar este comportamiento. ^[30]

Psicología

En el campo de la investigación sobre adicciones y la economía del comportamiento , George Ainslie señala que la adicción puede plantearse como un problema intertemporal de dilema del prisionero entre el yo presente y el futuro del adicto. En este caso, "desertar" significa recaer, y no recaer tanto hoy como en el futuro es, con diferencia, el mejor resultado. El caso en el que uno se abstiene hoy pero recae en el futuro es el peor resultado: en cierto sentido, la disciplina y el autosacrificio que implica la abstinencia hoy han sido "desperdiciados" porque la futura recaída significa que el adicto está de nuevo en el punto de partida y tendrá que empezar de nuevo. Recaer hoy y mañana es un resultado ligeramente "mejor", porque, aunque el adicto sigue siendo adicto, no ha hecho el esfuerzo de intentar dejarlo. El caso final, en el que uno se involucra en la conducta adictiva hoy mientras se abstiene mañana, tiene el problema de que (como en otros dilemas del prisionero) hay un beneficio obvio en desertar "hoy", pero mañana uno enfrentará el mismo dilema del prisionero, y el mismo beneficio obvio estará presente entonces, conduciendo en última instancia a una cadena interminable de deserciones. ^[31]

En The Science of Trust (La ciencia de la confianza) , John Gottman define las buenas relaciones como aquellas en las que los socios saben que no deben entrar en un comportamiento de deserción mutua, o al menos no quedarse estancados dinámicamente en él en un bucle. En la neurociencia cognitiva , la señalización cerebral rápida asociada con el procesamiento de diferentes rondas puede indicar opciones en la siguiente ronda. Los resultados de cooperación mutua implican cambios en la actividad cerebral que predicen la rapidez con la que una persona cooperará de la misma manera en la próxima oportunidad; ^[32] esta actividad puede estar vinculada a procesos homeostáticos y motivacionales básicos, posiblemente aumentando la probabilidad de tomar atajos hacia la cooperación mutua.

Ciencias económicas

El dilema del prisionero ha sido llamado la E. coli de la psicología social y se ha utilizado ampliamente para investigar diversos temas como la competencia oligopólica y la acción colectiva para producir un bien colectivo. ^[33]

La publicidad se cita a veces como un ejemplo real del dilema del prisionero. Cuando la publicidad de cigarrillos era legal en Estados Unidos, los fabricantes de cigarrillos que competían entre sí tenían que decidir cuánto dinero gastar en publicidad. La eficacia de la publicidad de la empresa A estaba determinada en parte por la publicidad realizada por la empresa B. Del mismo modo, el beneficio obtenido de la publicidad de la empresa B se ve afectado por la publicidad realizada por la empresa A. Si tanto la empresa A como la empresa B deciden hacer publicidad durante un período determinado, entonces la publicidad de cada empresa anula la de la otra, los ingresos permanecen constantes y los gastos aumentan debido al coste de la publicidad. Ambas empresas se beneficiarían de una reducción de la publicidad. Sin embargo, si la empresa B decide no hacer publicidad, la empresa A podría beneficiarse enormemente de la publicidad. No obstante, la cantidad óptima de publicidad de una empresa depende de la cantidad de publicidad que realice la otra. Como la mejor estrategia depende de lo que elija la otra empresa, no hay una estrategia dominante, lo que la hace ligeramente diferente de un dilema del prisionero. Sin embargo, el resultado es similar, en el sentido de que ambas empresas estarían en mejor situación si anunciaran menos que en el equilibrio.

A veces, en situaciones comerciales surgen comportamientos cooperativos. Por ejemplo, los fabricantes de cigarrillos respaldaron la promulgación de leyes que prohibieran la publicidad de cigarrillos, entendiendo que esto reduciría los costos y aumentaría las ganancias en toda la industria. ^{[34] [d]}

Sin acuerdos exigibles, los miembros de un cártel también se ven involucrados en un dilema del prisionero (en el que participan varios participantes). ^[35] "Cooperar" normalmente significa acordar un precio mínimo , mientras que "desertar" significa vender por debajo de ese nivel mínimo, quitándoles negocios instantáneamente a otros miembros del cártel. Las autoridades antimonopolio quieren que los posibles miembros del cártel se desistan mutuamente, asegurando los precios más bajos posibles para los consumidores.

Deporte

El dopaje en el deporte se ha citado como un ejemplo de dilema del prisionero. Dos atletas que compiten tienen la opción de utilizar una droga ilegal y/o peligrosa para mejorar su rendimiento. Si ninguno de los atletas toma la droga, entonces ninguno obtiene una ventaja. Si sólo uno lo hace, entonces ese atleta obtiene una ventaja significativa sobre el competidor, reducida por los peligros legales y/o médicos de haber tomado la droga. Pero si ambos atletas toman la droga, los beneficios se anulan y sólo quedan los peligros, poniéndolos a ambos en una posición peor que si ninguno se hubiera dopado. ^[36]

Política internacional

En la teoría de las relaciones internacionales , el dilema del prisionero se utiliza a menudo para demostrar por qué la cooperación fracasa en situaciones en las que la cooperación entre estados es colectivamente óptima pero individualmente subóptima. ^{[37] [38]} Un ejemplo clásico es el dilema de seguridad , por el cual un aumento en la seguridad de un estado (como aumentar su fuerza militar) lleva a otros estados a temer por su propia seguridad por temor a una acción ofensiva. ^[39] En consecuencia, las medidas de aumento de la seguridad pueden conducir a tensiones, escalada o conflicto con una o más partes, produciendo un resultado que ninguna de las partes desea realmente. ^{[40] [39] [41] [42] [43]} El dilema de seguridad es particularmente intenso en situaciones en las que es difícil distinguir las armas ofensivas de las defensivas, y la ofensiva tiene la ventaja en cualquier conflicto sobre la defensa. ^[39]

El dilema del prisionero ha sido frecuentemente utilizado por los teóricos realistas de las relaciones internacionales para demostrar por qué todos los estados (independientemente de sus políticas internas o ideología profesada) bajo la anarquía internacional tendrán dificultades para cooperar entre sí incluso cuando todos se benefician de dicha cooperación.

Los críticos del realismo sostienen que la iteración y la extensión de la sombra del futuro son soluciones al dilema del prisionero. Cuando los actores juegan el dilema del prisionero una vez, tienen incentivos para desertar, pero cuando esperan jugarlo repetidamente, tienen mayores incentivos para cooperar. ^[44]

Dilemas del modo multijugador

Muchos dilemas de la vida real involucran a múltiples jugadores. ^[45] Aunque metafórica, la tragedia de los comunes de Garrett Hardin puede verse como un ejemplo de una generalización del dilema del prisionero para múltiples jugadores: cada aldeano toma una decisión para su beneficio personal o para su moderación. La recompensa colectiva por la deserción unánime o frecuente es una recompensa muy baja y la destrucción de los comunes.

Los bienes comunes no siempre se explotan: William Poundstone , en un libro sobre el dilema del prisionero, describe una situación en Nueva Zelanda en la que las cajas de periódicos se dejan sin llave. Es posible que la gente tome un periódico sin pagar (desertar), pero muy pocos lo hacen, sintiendo que si no pagan, los demás tampoco lo harán, destruyendo el sistema. ^[46] Una investigación posterior de Elinor Ostrom , ganadora del Premio Nobel de Ciencias Económicas de 2009 , planteó la hipótesis de que la tragedia de los bienes comunes se simplifica demasiado, y que el resultado negativo está influenciado por influencias externas. Sin presiones complicadas, los grupos se comunican y gestionan los bienes comunes entre ellos para su beneficio mutuo, haciendo cumplir las normas sociales para preservar el recurso y lograr el máximo bien para el grupo, un ejemplo de cómo lograr el mejor resultado posible para el dilema del prisionero. ^{[47] [48]}

Entornos académicos

El dilema del prisionero se ha utilizado en diversos ámbitos académicos para ilustrar las complejidades de la cooperación y la competencia. Un ejemplo notable es el experimento en el aula realizado por el profesor de sociología Dan Chambliss en el Hamilton College en la década de 1980. A partir de 1981, Chambliss propuso que si ningún estudiante se presentaba al examen final, todos recibirían una A, pero si un solo estudiante lo hacía, los que no lo hicieran recibirían un cero. En 1988, John Werner , un estudiante de primer año, organizó con éxito a sus compañeros de clase para boicotear el examen, demostrando una aplicación práctica de la teoría de juegos y el concepto del dilema del prisionero. ^[49]

Casi 25 años después, en 2013, ocurrió un incidente similar en la Universidad Johns Hopkins. La política de calificación del profesor Peter Fröhlich escaló los exámenes finales según la puntuación más alta, lo que significa que si todos recibían la misma puntuación, todos obtendrían una A. Los estudiantes de las clases de Fröhlich organizaron un boicot al examen final, asegurándose de que nadie lo hiciera. Como resultado, todos los estudiantes recibieron una A, resolviendo con éxito el dilema del prisionero de una manera mutuamente óptima sin iteración. ^{[50] [51]} Estos ejemplos resaltan cómo se puede utilizar el dilema del prisionero para explorar el comportamiento cooperativo y la toma de decisiones estratégicas en contextos educativos.

Juegos relacionados

Intercambio de bolsa cerrada

El dilema del prisionero como intercambio de maletines

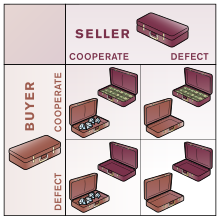
Douglas Hofstadter ^[52] sugirió que a menudo resulta más fácil entender problemas como el dilema del prisionero cuando se lo ilustra en forma de un juego simple o de un intercambio. Uno de los varios ejemplos que utilizó fue el del "intercambio de bolsas cerradas":

Dos personas se encuentran e intercambian bolsas cerradas, en el entendimiento de que una de ellas contiene dinero y la otra contiene una compra. Cualquiera de los jugadores puede optar por cumplir el trato colocando en su bolsa lo que acordaron o puede abandonar el trato entregando una bolsa vacía.

¿Amigo o enemigo?

¿Amigo o enemigo? es un concurso que se emitió entre 2002 y 2003 en la Game Show Network de Estados Unidos. En el concurso compiten tres parejas de personas. Cuando una pareja es eliminada, juegan un juego similar al dilema del prisionero para determinar cómo se dividen las ganancias. Si ambos cooperan (Amigo), comparten las ganancias 50-50. Si uno coopera y el otro se va (Enemigo), el que se va se queda con todas las ganancias y el que coopera no se lleva nada. Si ambos se van, ambos se van sin nada. Observe que la matriz de recompensas es ligeramente diferente de la estándar dada anteriormente, ya que las recompensas para los casos de "ambos se van" y "cooperan mientras el oponente se va" son idénticas. Esto hace que el caso de "ambos se van" sea un equilibrio débil, en comparación con el equilibrio estricto del dilema del prisionero estándar. Si un concursante sabe que su oponente va a votar "Enemigo", entonces su propia elección no afecta sus propias ganancias. En un sentido específico, Friend or Foe tiene un modelo de recompensas entre el dilema del prisionero y el juego del pollo .

Esta es la matriz de recompensas:

Esta matriz de pagos también se ha utilizado en los programas de televisión británicos Trust Me , Shafted , The Bank Job y Golden Balls , y en los concursos estadounidenses Take It All , así como para la pareja ganadora de los reality shows Bachelor Pad y Love Island . Los datos del juego de la serie Golden Balls han sido analizados por un equipo de economistas, que descubrieron que la cooperación era "sorprendentemente alta" para cantidades de dinero que parecerían importantes en el mundo real pero que eran comparativamente bajas en el contexto del juego. ^[53]

Ventisquero iterado

Investigadores de la Universidad de Lausana y la Universidad de Edimburgo han sugerido que el "juego iterado del ventisquero" puede reflejar con mayor precisión las situaciones sociales del mundo real, aunque este modelo es en realidad un juego de gallinas . En este modelo, el riesgo de ser explotado a través de la deserción es menor, y los individuos siempre ganan al elegir la opción cooperativa. El juego del ventisquero imagina a dos conductores que están atrapados en lados opuestos de un ventisquero , cada uno de los cuales tiene la opción de palear nieve para despejar un camino o permanecer en su automóvil. La mayor recompensa de un jugador proviene de dejar que el oponente limpie toda la nieve por sí solo, pero el oponente sigue siendo recompensado nominalmente por su trabajo.

Esto puede reflejar mejor situaciones del mundo real. Los investigadores dan el ejemplo de dos científicos que colaboran en un informe y ambos se beneficiarían si el otro trabajara más arduamente. "Pero cuando tu colaborador no hace ningún trabajo, probablemente sea mejor que hagas todo el trabajo tú mismo. De todos modos, terminarás con un proyecto terminado". ^{[54] [55]}

Juegos de coordinación

En los juegos de coordinación, los jugadores deben coordinar sus estrategias para obtener un buen resultado. Un ejemplo son dos coches que chocan de repente en medio de una tormenta de nieve; cada uno debe elegir si virar hacia la izquierda o hacia la derecha. Si ambos viran hacia la izquierda o hacia la derecha, los coches no chocan. La convención local de circulación por la izquierda y por la derecha ayuda a coordinar sus acciones.

Los juegos de coordinación simétrica incluyen " La caza del ciervo" y "Bach o Stravinsky" .

Dilemas del prisionero asimétricos

Un conjunto más general de juegos es el asimétrico. Como en el dilema del prisionero, el mejor resultado es la cooperación y existen motivos para la deserción. Sin embargo, a diferencia del dilema del prisionero simétrico, un jugador tiene más que perder y/o más que ganar que el otro. Algunos de estos juegos han sido descritos como un dilema del prisionero en el que un prisionero tiene una coartada , de ahí el término "juego de la coartada". ^[56]

En experimentos, los jugadores que obtienen pagos desiguales en juegos repetidos pueden tratar de maximizar las ganancias, pero sólo bajo la condición de que ambos jugadores reciban pagos iguales; esto puede conducir a una estrategia de equilibrio estable en la que el jugador en desventaja abandona cada juego X, mientras que el otro siempre coopera. Tal comportamiento puede depender de las normas sociales del experimento en torno a la justicia. ^[57]

Software

Se han creado varios paquetes de software para ejecutar simulaciones y torneos del dilema del prisionero, algunos de los cuales tienen su código fuente disponible:

• El código fuente del segundo torneo organizado por Robert Axelrod (escrito por Axelrod y muchos colaboradores en Fortran ) ^[58]
• Prison, ^[59] una biblioteca escrita en Java , actualizada por última vez en 1998
• Axelrod-Python, ^[60] escrito en Python
• Evoplex, ^[61] un programa de modelado rápido basado en agentes lanzado en 2018 por Marcos Cardinot

En la ficción

Hannu Rajaniemi ambientó la escena de apertura de su trilogía El ladrón cuántico en una "prisión de dilemas". El tema principal de la serie ha sido descrito como la "insuficiencia de un universo binario" y el antagonista final es un personaje llamado el Todo-Desertor. El primer libro de la serie se publicó en 2010, con dos secuelas, El príncipe fractal y El ángel causal , publicadas en 2012 y 2014, respectivamente.

Un juego inspirado en el dilema del prisionero iterado es el foco central del videojuego de 2012 Zero Escape: Virtue's Last Reward y una parte menor en su secuela de 2016 Zero Escape: Zero Time Dilemma .

En La misteriosa sociedad Benedict y el dilema del prisionero de Trenton Lee Stewart , los personajes principales comienzan jugando una versión del juego y escapan de la "prisión" por completo. Más tarde, se convierten en prisioneros reales y escapan una vez más.

En The Adventure Zone : Balance durante el subarco The Suffering Game , los personajes jugadores se enfrentan dos veces al dilema del prisionero durante su tiempo en el dominio de dos liches, una vez cooperando y otra desertando.

En la octava novela del autor James SA Corey, La ira de Tiamat , Winston Duarte le explica el dilema del prisionero a su hija de 14 años, Teresa, para entrenarla en el pensamiento estratégico. ^{[ cita requerida ]}

La película de 2008 The Dark Knight incluye una escena basada vagamente en el problema en el que el Joker manipula dos transbordadores, uno con prisioneros y el otro con civiles, armando a ambos grupos con los medios para detonar la bomba en los transbordadores del otro, amenazando con detonarlos a ambos si dudan. ^{[62] [63]}

En filosofía moral

El dilema del prisionero se utiliza comúnmente como herramienta de pensamiento en la filosofía moral como ilustración de la tensión potencial entre el beneficio del individuo y el beneficio de la comunidad.

Tanto el dilema del prisionero de una sola ronda como el dilema iterado tienen aplicaciones en la filosofía moral. De hecho, muchas de las situaciones morales, como el genocidio , no se repiten fácilmente más de una vez. Además, en muchas situaciones, los resultados de las rondas anteriores son desconocidos para los jugadores, ya que no son necesariamente los mismos (por ejemplo, la interacción con un mendigo en la calle). ^[64]

El filósofo David Gauthier utiliza el dilema del prisionero para mostrar cómo la moralidad y la racionalidad pueden entrar en conflicto. ^[65]

Algunos teóricos de juegos han criticado el uso del dilema del prisionero como herramienta de pensamiento en la filosofía moral. ^[65] Kenneth Binmore sostuvo que el dilema del prisionero no describe con precisión el juego que juega la humanidad, que, según él, se acerca más a un juego de coordinación . Brian Skyrms comparte esta perspectiva.

Steven Kuhn sugiere que estos puntos de vista pueden conciliarse considerando que el comportamiento moral puede modificar la matriz de pagos de un juego, transformándolo de un dilema del prisionero a otros juegos. ^[65]

Dilema del prisionero puro e impuro

El dilema del prisionero se considera "impuro" si una estrategia mixta puede dar mejores resultados esperados que una estrategia pura. Esto crea la interesante posibilidad de que la acción moral desde una perspectiva utilitarista (es decir, la que apunta a maximizar el bien de una acción) pueda requerir la aleatorización de la propia estrategia, como cooperar con un 80% de probabilidad y desertar con un 20% de probabilidad. ^[66]

Véase también

• Paradoja de Abilene
• Juego del ciempiés
• Problema de acción colectiva
• Exterioridad
• Teorema popular (teoría de juegos)
• Problema del polizón
• Juego de intercambio de regalos
• Trampa hobbesiana
• El dilema del prisionero inocente
• Juego de mentirosos
• Metajuego
• Dilema del prisionero opcional
• El dilema del prisionero y la cooperación
• Juego de bienes públicos
• Altruismo recíproco
• Búsqueda de rentas
• Preferencias sociales
• Superracionalidad
• Teoría de la confianza rápida
• La tragedia de los comunes
• El dilema del viajero
• El dilema del comensal sin escrúpulos

Notas

1. El torneo consta de dos rondas. En la primera, cada una de las ocho mejores estrategias fue buena, y ninguna de las siete peores fue buena. En la segunda ronda (los diseñadores de estrategias podrían tener en cuenta los resultados de la primera ronda), todas menos una de las quince mejores estrategias fueron buenas (y esa quedó en octavo lugar). De las quince peores estrategias, todas menos una no fueron buenas. ^[13]
2. A diferencia de estrategias como el grim trigger (también llamado Friedman), que nunca es el primero en desertar, sino una vez que el otro deserta aunque sea una vez, el grim trigger deserta a partir de ese momento. ^[14]
3. Por ejemplo, véase el estudio de 2003 ^[15] para un análisis del concepto y si puede aplicarse en situaciones económicas o estratégicas reales.
4. Este argumento a favor del desarrollo de la cooperación a través de la confianza se da en The Wisdom of Crowds , donde se sostiene que el capitalismo de larga distancia pudo formarse alrededor de un núcleo de cuáqueros , que siempre trataban honorablemente a sus socios comerciales (en lugar de desertar y renegar de sus promesas, un fenómeno que había desalentado los contratos anteriores de largo plazo e inaplicables en el extranjero). Se sostiene que los tratos con comerciantes confiables permitieron que el meme de la cooperación se extendiera a otros comerciantes, quienes lo difundieron aún más hasta que un alto grado de cooperación se convirtió en una estrategia rentable en el comercio general .

Referencias

1. "El dilema del prisionero". Stanford Encyclopedia of Philosophy . Consultado el 10 de marzo de 2024 .
2. Poundstone 1993, págs. 8, 117.
3. Poundstone 1993, pág. 118: "Una versión típica contemporánea de la historia es la siguiente: dos miembros de una banda criminal son arrestados y encarcelados. Cada prisionero está en confinamiento solitario sin medios para hablar o intercambiar mensajes con el otro. La policía admite que no tiene pruebas suficientes para condenar a la pareja por el cargo principal. Planean condenar a ambos a un año de prisión por un cargo menor. Al mismo tiempo, la policía ofrece a cada prisionero un trato fáustico. Si testifica contra su compañero, quedará libre, mientras que el compañero será condenado a tres años de prisión por el cargo principal. Ah, sí, hay una trampa... Si ambos prisioneros testifican uno contra el otro, ambos serán condenados a dos años de prisión. A los prisioneros se les da un poco de tiempo para pensarlo, pero en ningún caso ninguno puede saber lo que el otro ha decidido hasta que haya tomado su decisión irrevocablemente. A cada uno se le informa de que al otro prisionero se le ofrece exactamente el mismo trato. A cada prisionero sólo le preocupa su propio bienestar: minimizar su propia sentencia de prisión".
4. Poundstone 1993, pág. 118.
5. Grofman, Bernard; Pool, Jonathan (enero de 1977). "Cómo hacer de la cooperación la estrategia de optimización en un juego de dos personas". The Journal of Mathematical Sociology . 5 (2): 173–186. doi :10.1080/0022250x.1977.9989871. ISSN  0022-250X.
6. Shy, Oz (1995). Organización industrial: teoría y aplicaciones. Prensa del Instituto Tecnológico de Massachusetts. ISBN 978-0262193665. Recuperado el 27 de febrero de 2013 .
7. Aumann, Robert J. (2 de marzo de 2016), "16. Puntos aceptables en juegos cooperativos generales de n personas", Contribuciones a la teoría de juegos (AM-40), Volumen IV , Princeton University Press, págs. 287–324, doi :10.1515/9781400882168-018, ISBN 978-1-4008-8216-8, consultado el 14 de mayo de 2024
8. Cooper, Russell; DeJong, Douglas V.; Forsythe, Robert; Ross, Thomas W. (1996). "Cooperación sin reputación: evidencia experimental de los juegos del dilema del prisionero". Juegos y comportamiento económico . 12 (2): 187–218. doi :10.1006/game.1996.0013.
9. Dal Bó, Pedro; Fréchette, Guillaume R. (2019). "Elección de estrategia en el dilema del prisionero infinitamente repetido". American Economic Review . 109 (11): 3929–3952. doi :10.1257/aer.20181480. ISSN  0002-8282. S2CID  216726890.
10. Axelrod (2006), pág. 193
11. Axelrod (2006), pág. 31
12. Axelrod (2006), cap. 6
13. Axelrod (2006), págs. 113-114
14. Axelrod (2006), pág. 36
15. Landsberger, Michael; Tsirelson, Boris (2003). "Equilibrio de Nash bayesiano; una prueba estadística de la hipótesis" (PDF) . Universidad de Tel Aviv . Archivado desde el original (PDF) el 2 de octubre de 2005.
16. Wu, Jiadong; Zhao, Chengye (2019), Sun, Xiaoming; He, Kun; Chen, Xiaoyun (eds.), "Cooperación en la regla de Monte Carlo: el juego del dilema del prisionero en la red", Theoretical Computer Science , Communications in Computer and Information Science, vol. 1069, Springer Singapur, págs. 3–15, doi :10.1007/978-981-15-0105-0_1, ISBN 978-981-15-0104-3, Número de identificación del sujeto  118687103
17. Wedekind, C.; Milinski, M. (2 de abril de 1996). "Cooperación humana en el dilema del prisionero simultáneo y alterno: Pavlov versus el generoso ojo por ojo". Actas de la Academia Nacional de Ciencias . 93 (7): 2686–2689. Bibcode :1996PNAS...93.2686W. doi : 10.1073/pnas.93.7.2686 . PMC 39691 . PMID  11607644. 
18. "El equipo de la Universidad de Southampton gana la competición del dilema del prisionero" (Nota de prensa). Universidad de Southampton. 7 de octubre de 2004. Archivado desde el original el 21 de abril de 2014.
19. Press, WH; Dyson, FJ (26 de junio de 2012). "El dilema del prisionero iterado contiene estrategias que dominan a cualquier oponente evolutivo". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 109 (26): 10409–13. Bibcode :2012PNAS..10910409P. doi : 10.1073/pnas.1206569109 . PMC 3387070 . PMID  22615375. 
20. Adami, Christoph; Arend Hintze (2013). "La inestabilidad evolutiva de las estrategias de determinante cero demuestra que ganar no lo es todo". Nature Communications . 4 : 3. arXiv : 1208.2666 . Bibcode :2013NatCo...4.2193A. doi :10.1038/ncomms3193. PMC 3741637 . PMID  23903782. 
21. Hilbe, Christian; Martin A. Nowak; Karl Sigmund (abril de 2013). "Evolución de la extorsión en juegos iterados del dilema del prisionero". PNAS . 110 (17): 6913–18. arXiv : 1212.1067 . Bibcode :2013PNAS..110.6913H. doi : 10.1073/pnas.1214834110 . PMC 3637695 . PMID  23572576. 
22. Stewart, Alexander J.; Joshua B. Plotkin (2013). "De la extorsión a la generosidad, evolución en el dilema del prisionero iterado". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 110 (38): 15348–53. Bibcode :2013PNAS..11015348S. doi : 10.1073/pnas.1306246110 . PMC 3780848 . PMID  24003115. 
23. Akin, Ethan (2013). "Soluciones cooperativas estables para el dilema del prisionero iterado". pág. 9. arXiv : 1211.0969 [math.DS]. Código Bibliográfico :2012arXiv1211.0969A
24. Le S, Boyd R (2007). "Dinámica evolutiva del dilema del prisionero iterado continuo". Revista de biología teórica . 245 (2): 258–67. Bibcode :2007JThBi.245..258L. doi :10.1016/j.jtbi.2006.09.016. PMID  17125798.
25. Hammerstein, P. (2003). ¿Por qué la reciprocidad es tan poco frecuente en los animales sociales? Un llamamiento protestante. En: P. Hammerstein, Editor, Evolución genética y cultural de la cooperación, MIT Press. pp. 83–94.
26. "Mercados y datos". The Economist . 27 de septiembre de 2007.
27. Rehmeyer, Julie (29 de octubre de 2012). "La teoría de juegos sugiere que las actuales negociaciones sobre el clima no evitarán la catástrofe". Noticias de ciencia . Sociedad para la ciencia y el público.
28. Osang, Thomas; Nandyyz, Arundhati (agosto de 2003). Regulación ambiental de empresas contaminantes: revisión de la hipótesis de Porter (PDF) (documento). Archivado (PDF) desde el original el 2 de julio de 2010.
29. Brosnan, Sarah F.; Earley, Ryan L.; Dugatkin, Lee A. (octubre de 2003). "Aprendizaje observacional e inspección de depredadores en guppies (Poecilia reticulata): aprendizaje social en guppies". Ethology . 109 (10): 823–833. doi : 10.1046/j.0179-1613.2003.00928.x .
30. Dawkins, Richard (1976). El gen egoísta . Oxford University Press.
31. Ainslie, George (2001). El colapso de la voluntad . Cambridge University Press. ISBN 978-0-521-59694-7.
32. Cervantes Constantino, Garat, Nicolaisen, Paz, Martínez-Montes, Kessel, Cabana y Gradin (2020). "El procesamiento neuronal de los resultados iterados del dilema del prisionero indica la elección de la siguiente ronda y la velocidad para corresponder a la cooperación". Neurociencia social . 16 (2): 103–120. doi :10.1080/17470919.2020.1859410. PMID  33297873. S2CID  228087900.{{cite journal}}: CS1 maint: multiple names: authors list (link)
33. Axelrod, Robert (1980). "Elección eficaz en el dilema del prisionero". Revista de resolución de conflictos . 24 (1): 3–25. doi :10.1177/002200278002400101. ISSN  0022-0027. JSTOR  173932. S2CID  143112198.
34. Henriksen, Lisa (marzo de 2012). "Restricciones integrales a la comercialización del tabaco: promoción, empaquetado, precio y plaza". Tobacco Control . 21 (2): 147–153. doi :10.1136/tobaccocontrol-2011-050416. PMC 4256379 . PMID  22345238. 
35. Nicholson, Walter (2000). Microeconomía intermedia y su aplicación (8.ª ed.). Fort Worth, TX: Dryden Press : Harcourt College Publishers. ISBN 978-0-030-25916-6.
36. Schneier, Bruce (26 de octubre de 2012). "Lance Armstrong y el dilema del prisionero del dopaje en los deportes profesionales". Wired . Wired.com . Consultado el 29 de octubre de 2012 .
37. Snyder, Glenn H. (1971). "El dilema del prisionero" y los modelos "pollo" en la política internacional". International Studies Quarterly . 15 (1): 66–103. doi :10.2307/3013593. ISSN  0020-8833. JSTOR  3013593.
38. Jervis, Robert (1978). "Cooperación bajo el dilema de la seguridad". Política mundial . 30 (2): 167–214. doi :10.2307/2009958. hdl : 2027/uc1.31158011478350 . ISSN  1086-3338. JSTOR  2009958. S2CID  154923423.
39. Jervis, Robert (1978). "Cooperación ante el dilema de la seguridad". Política mundial . 30 (2): 167–214. doi :10.2307/2009958. hdl : 2027/uc1.31158011478350 . ISSN  0043-8871. JSTOR  2009958. S2CID  154923423.
40. Herz, John H. (1950). El internacionalismo idealista y el dilema de la seguridad . págs. 157–180.
41. Snyder, Glenn H. (1984). "El dilema de la seguridad en la política de alianzas". Política mundial . 36 (4): 461–495. doi :10.2307/2010183. ISSN  0043-8871. JSTOR  2010183. S2CID  154759602.
42. Jervis, Robert (1976). Percepción y percepción errónea en la política internacional. Princeton University Press. pp. 58-113. ISBN 978-0-691-10049-4.
43. Glaser, Charles L. (2010). Teoría racional de la política internacional. Princeton University Press. ISBN 9780691143729.
44. Axelrod, Robert; Hamilton, William D. (1981). "La evolución de la cooperación". Science . 211 (4489): 1390–1396. Bibcode :1981Sci...211.1390A. doi :10.1126/science.7466396. ISSN  0036-8075. PMID  7466396.
45. Gokhale CS, Traulsen A. Juegos evolutivos en el multiverso. Actas de la Academia Nacional de Ciencias. 23 de marzo de 2010. 107(12):5500–04.
46. Poundstone 1993, págs. 126-127.
47. "La conspiración de Volokh " Elinor Ostrom y la tragedia de los comunes". Volokh.com. 2009-10-12 . Consultado el 2011-12-17 .
48. Ostrom, Elinor (2015) [1990]. Gobernar los bienes comunes: la evolución de las instituciones para la acción colectiva . Cambridge University Press. doi :10.1017/CBO9781316423936. ISBN. 978-1-107-56978-2.
49. Rivard, Ry (21 de febrero de 2013). "Una mirada retrospectiva a otro exitoso boicot de exámenes finales". Inside Higher Ed . Consultado el 12 de julio de 2024 .
50. Wolfers, Justin (14 de febrero de 2013). "Gaming the System" (Cómo jugar con el sistema). The New York Times . Consultado el 12 de julio de 2024 .
51. "Estudiantes de Johns Hopkins boicotean examen final para que todos obtengan una A". Baltimore Fishbowl. 2013-02-25 . Consultado el 2024-07-12 .
52. Hofstadter, Douglas R. (1985). "Cap. 29 El dilema del prisionero Los torneos informáticos y la evolución de la cooperación ". Temas metamágicos: en busca de la esencia de la mente y los patrones . Bantam Dell Pub Group. ISBN 978-0-465-04566-2.
53. Van den Assem, Martijn J. (enero de 2012). "¿Dividir o robar? Comportamiento cooperativo cuando hay mucho en juego". Management Science . 58 (1): 2–20. doi :10.1287/mnsc.1110.1413. hdl : 1765/31292 . S2CID  1371739. SSRN  1592456.
54. Zyga, Lisa (9 de octubre de 2007). "El juego 'Snowdrift' supera al 'Dilema del Prisionero' en la explicación de la cooperación". Phys.org . Archivado desde el original el 11 de abril de 2024.
55. Kümmerli, Rolf; Colliard, Caroline; Fiechter, Nicolas; Petitpierre, Blaise; Russier, Flavien; Keller, Laurent (25 de septiembre de 2007). "Cooperación humana en dilemas sociales: comparación del juego Snowdrift con el dilema del prisionero". Actas de la Royal Society B: Ciencias Biológicas . 274 (1628). Royal Society: 2965–2970. doi :10.1098/rspb.2007.0793. ISSN  1471-2954. PMC 2291152 . PMID  17895227. 
56. Robinson, DR; Goforth, DJ (5 de mayo de 2004). Juegos de coartadas: los dilemas asimétricos del prisionero (PDF) . Reuniones de la Asociación Canadiense de Economía, Toronto, 4-6 de junio de 2004. Archivado (PDF) desde el original el 6 de diciembre de 2004.
57. Beckenkamp, ​​Martin; Hennig-Schmidt, Heike; Maier-Rigaud, Frank P. (4 de marzo de 2007). "Cooperación en juegos de dilema del prisionero simétricos y asimétricos" (PDF) . Instituto Max Planck para la Investigación de Bienes Colectivos . Archivado (PDF) desde el original el 2 de septiembre de 2019.
58. Disponible en línea en http://www-personal.umich.edu/~axe/research/Software/CC/CC2.html
59. https://web.archive.org/web/19991010053242/http://www.lifl.fr/IPD/ipd.frame.html
60. https://github.com/Axelrod-Python/Axelrod
61. https://evoplex.org/
62. Romain, Lindsey (18 de julio de 2018). «El único personaje redimible de El caballero oscuro es el criminal que salva los transbordadores». Polygon . Consultado el 6 de enero de 2024 .
63. "Blog del curso The Dark Knight: Game Theory: Networks para INFO 2040/CS 2850/Econ 2040/SOC 2090" . Consultado el 6 de enero de 2024 .
64. Kuhn, Steven T. (1 de julio de 2004). "Reflexiones sobre ética y teoría de juegos". Síntesis . 141 (1): 1–44. doi :10.1023/B:SYNT.0000035846.91195.cb. ISSN  1573-0964.
65. Kuhn, Steven (diciembre de 2016). "Gauthier y el dilema del prisionero". Diálogo . 55 (4): 659–676. doi :10.1017/S0012217316000603. ISSN  0012-2173.
66. Kuhn, Steven T.; Moresi, Serge (octubre de 1995). "Dilemas del prisionero puros y utilitaristas". Economía y filosofía . 11 (2): 333–343. doi :10.1017/S0266267100003424. ISSN  0266-2671.

Bibliografía

• Poundstone, William (1993). El dilema del prisionero (1.ª edición de Anchor Books). Nueva York: Anchor. ISBN 0-385-41580-X.

Lectura adicional

• Amadae, S. (2016). "El dilema del prisionero", Prisoners of Reason . Cambridge University Press , NY, págs. 24–61.
• Aumann, Robert (1959). "Puntos aceptables en juegos cooperativos generales de n personas". En Luce, RD; Tucker, AW (eds.). Contribuciones a la teoría de los juegos IV . Anales del estudio de las matemáticas. Vol. 40. Princeton, NJ: Princeton University Press. págs. 287–324. MR  0104521.
• Axelrod, Robert (2006). La evolución de la cooperación (edición revisada). Basic Books. ISBN 0-465-00564-0.
• Bicchieri, Cristina (1993). Racionalidad y coordinación. Cambridge University Press .
• Chess, David M. (diciembre de 1988). "Simulación de la evolución del comportamiento: el problema del dilema del prisionero iterado" (PDF) . Complex Systems . 2 (6): 663–70. Archivado (PDF) desde el original el 30 de mayo de 2015.
• Collins, Rory W. (marzo de 2022). «La paradoja del dilema del prisionero: racionalidad, moralidad y reciprocidad». Think: Philosophy for Everyone . 21 (61): 45–55. doi : 10.1017/S1477175621000464 .
• Dresher, M. (1961). Las matemáticas de los juegos de estrategia: teoría y aplicaciones Prentice-Hall , Englewood Cliffs, NJ.
• Greif, A. (2006). Instituciones y el camino hacia la economía moderna: lecciones del comercio medieval. Cambridge University Press, Cambridge , Reino Unido.
• Kopelman, Shirli (febrero de 2020). "Ojo por ojo y más allá: el trabajo legendario de Anatol Rapoport". Investigación sobre negociación y gestión de conflictos . 13 (1): 60–84. doi : 10.1111/ncmr.12172 . hdl : 2027.42/153763 .
• Rapoport, Anatol y Albert M. Chammah (1965). El dilema del prisionero . University of Michigan Press .
• Schneider, Mark; Shields, Timothy W. (junio de 2022). "Motivos para la cooperación en el dilema del prisionero de un solo uso". Revista de finanzas conductuales . 23 (4): 438–456. doi :10.1080/15427560.2022.2081974. S2CID  249903572.

Enlaces externos

• Medios relacionados con El dilema del prisionero en Wikimedia Commons
• El dilema del prisionero en ornitología: caricatura matemática de Larry Gonick.
• Dixit, Avinash ; Nalebuff, Barry (2008). "El dilema del prisionero". En David R. Henderson (ed.). Enciclopedia concisa de economía (2.ª ed.). Indianápolis: Biblioteca de Economía y Libertad . ISBN 978-0865976658.OCLC 237794267  .
• Dawkins: Los buenos chicos acaban primero
• Biblioteca de Python para el dilema del prisionero iterado de Axelrod
• Juega al dilema del prisionero en oTree (N/A 11-5-17)
• La evolución de la confianza de Nicky Case, un ejemplo del juego de la donación
• Juego en línea El dilema del prisionero iterado por Wayne Davis
• Lo que el dilema del prisionero revela sobre la vida, el universo y todo lo demás, por Veritasium