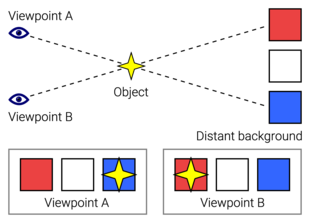
El paralaje es un desplazamiento o diferencia en la posición aparente de un objeto visto a lo largo de dos líneas de visión diferentes y se mide por el ángulo o semiángulo de inclinación entre esas dos líneas. [1] [2] Debido al escorzo , los objetos cercanos muestran un paralaje mayor que los objetos más lejanos, por lo que el paralaje se puede utilizar para determinar distancias.
Para medir grandes distancias, como la distancia de un planeta o una estrella a la Tierra , los astrónomos utilizan el principio de paralaje. Aquí, el término paralaje es el semiángulo de inclinación entre dos líneas de visión hacia la estrella, como se observa cuando la Tierra está en lados opuestos del Sol en su órbita. [a] Estas distancias forman el peldaño más bajo de lo que se llama "la escalera de distancias cósmicas ", el primero de una sucesión de métodos mediante los cuales los astrónomos determinan las distancias a los objetos celestes, que sirve como base para otras mediciones de distancia en astronomía que forman los peldaños más altos de la escalera.
El paralaje también afecta a instrumentos ópticos como miras telescópicas, binoculares , microscopios y cámaras réflex de doble lente que ven objetos desde ángulos ligeramente diferentes. Muchos animales, junto con los humanos, tienen dos ojos con campos visuales superpuestos que utilizan el paralaje para obtener percepción de profundidad ; este proceso se conoce como estereopsis . En visión por computadora , el efecto se utiliza para la visión estereoscópica por computadora , y hay un dispositivo llamado telémetro de paralaje que lo utiliza para encontrar la distancia y, en algunas variaciones, también la altitud a un objetivo.
Un ejemplo cotidiano y sencillo de paralaje se puede ver en los tableros de instrumentos de los vehículos de motor que utilizan un velocímetro mecánico de tipo aguja. Cuando se observa directamente desde el frente, la velocidad puede mostrar exactamente 60, pero cuando se observa desde el asiento del pasajero, la aguja puede parecer mostrar una velocidad ligeramente diferente debido al ángulo de visión combinado con el desplazamiento de la aguja con respecto al plano del dial numérico.

Debido a que los ojos de los humanos y de otros animales están en diferentes posiciones en la cabeza, presentan diferentes vistas simultáneamente. Esta es la base de la estereopsis , el proceso por el cual el cerebro explota la paralaje debido a las diferentes vistas desde el ojo para obtener percepción de profundidad y estimar distancias a los objetos. [3]
Los animales también utilizan la paralaje de movimiento , en la que los animales (o solo la cabeza) se mueven para obtener diferentes puntos de vista. Por ejemplo, las palomas (cuyos ojos no tienen campos de visión superpuestos y, por lo tanto, no pueden usar la estereopsis) mueven sus cabezas hacia arriba y hacia abajo para ver la profundidad. [4] La paralaje de movimiento también se explota en la estereoscopía de meneo , gráficos de computadora que brindan pistas de profundidad a través de una animación que cambia el punto de vista en lugar de a través de la visión binocular.

La paralaje se produce debido a un cambio en el punto de vista que se produce debido al movimiento del observador, de lo observado o de ambos. Lo esencial es el movimiento relativo. Observando la paralaje, midiendo ángulos y utilizando la geometría , se puede determinar la distancia .
La medición de distancias por paralaje es un caso especial del principio de triangulación , que establece que se pueden calcular todos los lados y ángulos de una red de triángulos si, además de todos los ángulos de la red, se ha medido la longitud de al menos un lado. Por lo tanto, la medición cuidadosa de la longitud de una línea base puede fijar la escala de toda una red de triangulación. En paralaje, el triángulo es extremadamente largo y estrecho, y midiendo tanto su lado más corto (el movimiento del observador) como el ángulo superior pequeño (siempre menor a 1 segundo de arco , [5] dejando los otros dos cerca de 90 grados), se puede determinar la longitud de los lados largos (en la práctica considerados iguales).
En astronomía, asumiendo que el ángulo es pequeño, la distancia a una estrella (medida en parsecs ) es el recíproco de la paralaje (medida en segundos de arco ): por ejemplo, la distancia a Próxima Centauri es 1/0,7687 = 1,3009 parsecs (4,243 años luz). [6]
En la Tierra, se puede utilizar un telémetro de coincidencia o de paralaje para encontrar la distancia a un objetivo. En topografía , el problema de la resección explora las mediciones angulares a partir de una línea base conocida para determinar las coordenadas de un punto desconocido.
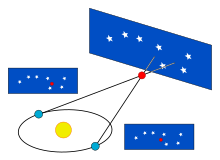
Las medidas de distancia fundamentales más importantes en astronomía provienen de la paralaje trigonométrico, tal como se aplica en el método de paralaje estelar . A medida que la Tierra orbita alrededor del Sol, la posición de las estrellas cercanas parecerá desplazarse ligeramente con respecto al fondo más distante. Estos desplazamientos son ángulos en un triángulo isósceles , con 2 UA (la distancia entre las posiciones extremas de la órbita de la Tierra alrededor del Sol) formando el cateto base del triángulo y la distancia a la estrella siendo los catetos largos de igual longitud. La cantidad de desplazamiento es bastante pequeña, incluso para las estrellas más cercanas, midiendo 1 segundo de arco para un objeto a una distancia de 1 pársec (3,26 años luz ), y luego disminuyendo en cantidad angular a medida que aumenta la distancia. Los astrónomos generalmente expresan las distancias en unidades de pársecs (segundos de arco de paralaje); los años luz se utilizan en los medios populares.
Debido a que la paralaje se hace más pequeña a mayor distancia estelar, las distancias útiles pueden medirse sólo para estrellas que están lo suficientemente cerca como para tener una paralaje mayor que unas pocas veces la precisión de la medición. En la década de 1990, por ejemplo, la misión Hipparcos obtuvo paralajes para más de cien mil estrellas con una precisión de alrededor de un milisegundo de arco , [7] proporcionando distancias útiles para estrellas de hasta unos pocos cientos de parsecs. La Wide Field Camera 3 del telescopio espacial Hubble tiene el potencial de proporcionar una precisión de 20 a 40 microsegundos de arco, lo que permite mediciones de distancias confiables de hasta 5000 parsecs (16 000 años luz) para pequeñas cantidades de estrellas. [8] [9] La misión espacial Gaia proporcionó distancias igualmente precisas para la mayoría de las estrellas más brillantes que la magnitud 15. [10]
Las distancias se pueden medir con un margen de error del 10% hasta el centro galáctico , a unos 30.000 años luz de distancia. Las estrellas tienen una velocidad relativa al Sol que provoca un movimiento propio (transversal a través del cielo) y una velocidad radial (movimiento hacia o desde el Sol). La primera se determina trazando la posición cambiante de las estrellas a lo largo de muchos años, mientras que la segunda proviene de la medición del desplazamiento Doppler del espectro de la estrella causado por el movimiento a lo largo de la línea de visión. Para un grupo de estrellas con la misma clase espectral y un rango de magnitud similar, se puede derivar una paralaje media a partir del análisis estadístico de los movimientos propios relativos a sus velocidades radiales. Este método de paralaje estadístico es útil para medir las distancias de estrellas brillantes más allá de los 50 parsecs y estrellas variables gigantes , incluidas las cefeidas y las variables RR Lyrae . [11]


El movimiento del Sol a través del espacio proporciona una línea de base más larga que aumentará la precisión de las mediciones de paralaje, conocida como paralaje secular . Para las estrellas en el disco de la Vía Láctea , esto corresponde a una línea de base media de 4 UA por año, mientras que para las estrellas del halo la línea de base es de 40 UA por año. Después de varias décadas, la línea de base puede ser órdenes de magnitud mayor que la línea de base Tierra-Sol utilizada para el paralaje tradicional. Sin embargo, el paralaje secular introduce un mayor nivel de incertidumbre porque la velocidad relativa de las estrellas observadas es una incógnita adicional. Cuando se aplica a muestras de múltiples estrellas, la incertidumbre se puede reducir; la incertidumbre es inversamente proporcional a la raíz cuadrada del tamaño de la muestra. [14]
La paralaje de cúmulos móviles es una técnica que permite utilizar los movimientos de estrellas individuales en un cúmulo estelar cercano para determinar la distancia al cúmulo. Solo los cúmulos abiertos están lo suficientemente cerca como para que esta técnica sea útil. En particular, la distancia obtenida para las Híades ha sido históricamente un paso importante en la escala de distancias.
En circunstancias especiales, se pueden realizar estimaciones de distancias fundamentales para otros objetos individuales. Si se puede observar la expansión de una nube de gas, como un remanente de supernova o una nebulosa planetaria , a lo largo del tiempo, se puede estimar una distancia de paralaje de expansión hasta esa nube. Sin embargo, esas mediciones sufren incertidumbres en la desviación del objeto de la esfericidad. Las estrellas binarias , que son binarias tanto visuales como espectroscópicas, también pueden tener su distancia estimada por medios similares y no sufren la incertidumbre geométrica mencionada anteriormente. La característica común de estos métodos es que se combina una medición del movimiento angular con una medición de la velocidad absoluta (generalmente obtenida a través del efecto Doppler ). La estimación de la distancia proviene del cálculo de qué tan lejos debe estar el objeto para que su velocidad absoluta observada aparezca con el movimiento angular observado.
En particular, las paralajes de expansión pueden proporcionar estimaciones fundamentales de la distancia para objetos que están muy lejos, porque los eyectados de supernova tienen grandes velocidades de expansión y tamaños grandes (en comparación con las estrellas). Además, pueden observarse con interferómetros de radio que pueden medir movimientos angulares muy pequeños. Estos se combinan para proporcionar estimaciones fundamentales de la distancia a las supernovas en otras galaxias. [15] Aunque valiosos, estos casos son bastante raros, por lo que sirven como comprobaciones de consistencia importantes en la escala de distancias en lugar de ser pasos de batalla por sí mismos.Las mediciones realizadas observando la posición de un marcador en relación con algo que se va a medir están sujetas a un error de paralaje si el marcador está a cierta distancia del objeto de medición y no se observa desde la posición correcta. Por ejemplo, si se mide la distancia entre dos marcas en una línea con una regla marcada en su superficie superior, el grosor de la regla separará sus marcas de las marcas. Si se observa desde una posición que no es exactamente perpendicular a la regla, la posición aparente se desplazará y la lectura será menos precisa de lo que la regla es capaz de ofrecer.
Un error similar ocurre cuando se lee la posición de un puntero en una escala en un instrumento como un multímetro analógico . Para ayudar al usuario a evitar este problema, la escala a veces se imprime sobre una tira estrecha de espejo y el ojo del usuario se coloca de manera que el puntero oculte su reflejo, garantizando que la línea de visión del usuario sea perpendicular al espejo y, por lo tanto, a la escala. El mismo efecto altera la velocidad leída en el velocímetro de un automóvil por un conductor que va delante de él y un pasajero que va a un lado, los valores leídos en una retícula que no están en contacto real con la pantalla de un osciloscopio , etc.
Cuando se observan a través de un visor estereoscópico, las imágenes aéreas ofrecen un efecto estereoscópico pronunciado del paisaje y los edificios. Los edificios altos parecen "inclinarse" en la dirección opuesta al centro de la fotografía. Las mediciones de esta paralaje se utilizan para deducir la altura de los edificios, siempre que se conozcan la altura de vuelo y las distancias de referencia. Este es un componente clave del proceso de fotogrametría .
El error de paralaje se puede observar al tomar fotografías con muchos tipos de cámaras, como las cámaras réflex de doble lente y las que incluyen visores (como las cámaras con telémetro ). En estas cámaras, el ojo ve el sujeto a través de una óptica diferente (el visor o una segunda lente) que aquella a través de la cual se toma la fotografía. Como el visor a menudo se encuentra encima del lente de la cámara, las fotos con error de paralaje a menudo son ligeramente más bajas de lo previsto, siendo el ejemplo clásico la imagen de una persona con la cabeza recortada. Este problema se soluciona en las cámaras réflex de lente única , en las que el visor ve a través del mismo lente a través del cual se toma la fotografía (con la ayuda de un espejo móvil), evitando así el error de paralaje.
El paralaje también es un problema en la unión de imágenes , como en las panorámicas.
El paralaje afecta a los dispositivos de puntería de las armas de largo alcance de muchas maneras. En las miras instaladas en armas pequeñas y arcos , etc., la distancia perpendicular entre la mira y el eje de lanzamiento del arma (por ejemplo, el eje del ánima de un arma), generalmente denominada " altura de la mira ", puede inducir errores de puntería significativos al disparar a corta distancia, en particular cuando se dispara a objetivos pequeños. [16] Este error de paralaje se compensa (cuando es necesario) mediante cálculos que también tienen en cuenta otras variables como la caída de la bala , la desviación del viento y la distancia a la que se espera que esté el objetivo. [17] La altura de la mira se puede utilizar de forma ventajosa al "alinear" los rifles para su uso en el campo. Un rifle de caza típico (.222 con miras telescópicas) ajustado a 75 m seguirá siendo útil desde 50 a 200 m (55 a 219 yd) sin necesidad de ajustes adicionales. [ cita requerida ]
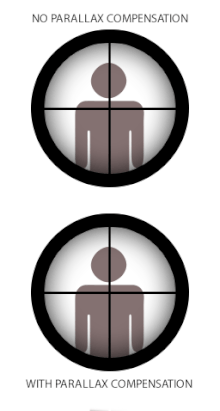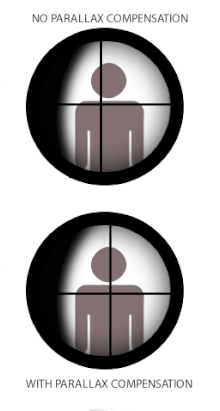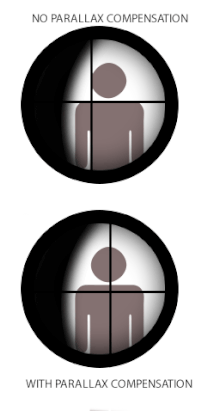
En algunos instrumentos ópticos reticulados , como telescopios , microscopios o miras telescópicas ("scopes") utilizadas en armas pequeñas y teodolitos , el paralaje puede crear problemas cuando la retícula no coincide con el plano focal de la imagen del objetivo. Esto se debe a que cuando la retícula y el objetivo no están en el mismo foco, las distancias ópticamente correspondientes que se proyectan a través del ocular también son diferentes, y el ojo del usuario registrará la diferencia en paralajes entre la retícula y el objetivo (siempre que cambie la posición del ojo) como un desplazamiento relativo uno sobre el otro. El término cambio de paralaje se refiere a los movimientos "flotantes" aparentes resultantes de la retícula sobre la imagen del objetivo cuando el usuario mueve su cabeza/ojo lateralmente (arriba/abajo o izquierda/derecha) detrás de la mira, [18] es decir, un error en el que la retícula no permanece alineada con el eje óptico del usuario .
Algunas miras telescópicas para armas de fuego están equipadas con un mecanismo de compensación de paralaje, que consiste en un elemento óptico móvil que permite al sistema óptico cambiar el foco de la imagen del objetivo a diferentes distancias en el mismo plano óptico de la retícula (o viceversa). Muchas miras telescópicas de gama baja pueden no tener compensación de paralaje porque en la práctica aún pueden funcionar de manera muy aceptable sin eliminar el cambio de paralaje. En este caso, la mira se fija a menudo a una distancia libre de paralaje designada que mejor se adapte a su uso previsto. Las distancias libres de paralaje estándar de fábrica típicas para las miras de caza son 100 yd (o 90 m) para que sean adecuadas para tiros de caza que rara vez superan los 300 yd/m. Algunas miras telescópicas de competición y de estilo militar sin compensación de paralaje pueden ajustarse para que no tengan paralaje a distancias de hasta 300 yd/m para que sean más adecuadas para apuntar a distancias más largas. [ cita requerida ] Las miras telescópicas para armas con alcances prácticos más cortos, como las pistolas de aire comprimido , los rifles de percusión anular , las escopetas y los rifles de avancarga , tendrán ajustes de paralaje para distancias más cortas, comúnmente 50 m (55 yd) para las miras telescópicas de percusión anular y 100 m (110 yd) para las escopetas y los rifles de avancarga. [ cita requerida ] Las miras telescópicas para armas de aire comprimido se encuentran muy a menudo con paralaje ajustable, generalmente en forma de un diseño de objetivo ajustable (o "AO" para abreviar), y pueden ajustarse hasta cerca de 3 metros (3,3 yd). [ cita requerida ]
Las miras reflectoras sin aumento o "réflex" pueden ser teóricamente "libres de paralaje". Pero como estas miras utilizan luz colimada paralela , esto solo es cierto cuando el objetivo está en el infinito. A distancias finitas, el movimiento del ojo perpendicular al dispositivo provocará un movimiento de paralaje en la imagen de la retícula en relación exacta con la posición del ojo en la columna cilíndrica de luz creada por la óptica colimadora. [19] [20] Las miras de armas de fuego, como algunas miras de punto rojo , intentan corregir esto al no enfocar la retícula en el infinito, sino en una distancia finita, un rango de objetivo diseñado donde la retícula mostrará muy poco movimiento debido al paralaje. [19] Algunos fabricantes comercializan modelos de miras reflectoras que denominan "libres de paralaje", [21] pero esto se refiere a un sistema óptico que compensa la aberración esférica fuera del eje , un error óptico inducido por el espejo esférico utilizado en la mira que puede causar que la posición de la retícula se desvíe del eje óptico de la mira con el cambio en la posición del ojo. [22] [23]
Debido a la posición de los cañones de artillería naval o de campaña , cada uno tiene una perspectiva ligeramente diferente del objetivo en relación con la ubicación del propio sistema de control de tiro . Por lo tanto, al apuntar sus cañones al objetivo, el sistema de control de tiro debe compensar el paralaje para asegurar que el fuego de cada cañón converja en el objetivo.
Varias de las obras escultóricas de Mark Renn juegan con el paralaje y parecen abstractas hasta que se las observa desde un ángulo específico. Una de esas esculturas es The Darwin Gate (en la imagen) en Shrewsbury , Inglaterra, que desde un cierto ángulo parece formar una cúpula, según Historic England , en "la forma de un casco sajón con una ventana normanda... inspirada en las características de la iglesia de Santa María a la que asistía Charles Darwin cuando era niño". [24]
En un sentido filosófico/geométrico: un cambio aparente en la dirección de un objeto, causado por un cambio en la posición de observación que proporciona una nueva línea de visión. El desplazamiento aparente, o diferencia de posición, de un objeto, visto desde dos estaciones o puntos de vista diferentes. En la escritura contemporánea, la paralaje también puede ser la misma historia, o una historia similar de aproximadamente la misma línea de tiempo, de un libro, contada desde una perspectiva diferente en otro libro. La palabra y el concepto ocupan un lugar destacado en la novela de James Joyce de 1922, Ulises . Orson Scott Card también utilizó el término al referirse a La sombra de Ender en comparación con El juego de Ender .
La metáfora es invocada por el filósofo esloveno Slavoj Žižek en su libro de 2006 The Parallax View , tomando prestado el concepto de "visión de paralaje" del filósofo y crítico literario japonés Kojin Karatani . Žižek señala
El giro filosófico que hay que añadir (al paralaje), por supuesto, es que la distancia observada no es simplemente "subjetiva", puesto que el mismo objeto que existe "ahí afuera" se ve desde dos posturas o puntos de vista diferentes. Se trata más bien de que, como diría Hegel , sujeto y objeto están inherentemente "mediados", de modo que un cambio " epistemológico " en el punto de vista del sujeto siempre refleja un cambio " ontológico " en el objeto mismo. O, para decirlo en términos lacanianos , la mirada del sujeto siempre está ya inscrita en el objeto percibido mismo, bajo la apariencia de su "punto ciego", aquello que está "en el objeto más que en el objeto mismo", el punto desde el cual el objeto mismo devuelve la mirada. "Claro que la imagen está en mi ojo, pero yo también estoy en la imagen"... [25]
- Slavoj Žižek, La visión del paralaje
Inclinación mutua de dos líneas que se encuentran en un ángulo.
Astron.
Desplazamiento aparente, o diferencia en la posición aparente, de un objeto, causado por un cambio real (o diferencia) de la posición del punto de observación; espec. la cantidad angular de dicho desplazamiento o diferencia de posición, siendo el ángulo contenido entre las dos líneas rectas trazadas hacia el objeto desde los dos puntos de vista diferentes y constituyendo una medida de la distancia del objeto.
{{cite web}}: CS1 maint: nombres numéricos: lista de autores ( enlace )