Oscilador de relajación

Oscilador que produce una forma de onda repetitiva no sinusoidal

Oscilador de relajación simple creado realimentando el voltaje de salida de un disparador Schmitt inversor a través de una red RC a su entrada.

En electrónica , un oscilador de relajación es un circuito oscilador electrónico no lineal que produce una señal de salida repetitiva no sinusoidal , como una onda triangular o una onda cuadrada . ^{[1] [2] [3] [4]} El circuito consta de un bucle de retroalimentación que contiene un dispositivo de conmutación como un transistor , comparador , relé , ^[5] amplificador operacional o un dispositivo de resistencia negativa como un diodo túnel , que carga repetidamente un capacitor o inductor a través de una resistencia hasta que alcanza un nivel umbral, luego lo descarga nuevamente. ^{[4] [6]} El período del oscilador depende de la constante de tiempo del circuito del capacitor o inductor. ^[2] El dispositivo activo cambia abruptamente entre los modos de carga y descarga, y por lo tanto produce una forma de onda repetitiva que cambia de manera discontinua. ^{[2] [4]} Esto contrasta con el otro tipo de oscilador electrónico, el oscilador armónico o lineal , que utiliza un amplificador con retroalimentación para excitar oscilaciones resonantes en un resonador , produciendo una onda sinusoidal . ^[7]

La señal de giro intermitente de algunos vehículos de motor se genera mediante un simple oscilador de relajación que alimenta un relé .

Los osciladores de relajación se pueden utilizar para una amplia gama de frecuencias, pero como son uno de los tipos de osciladores adecuados para frecuencias bajas, por debajo del audio, normalmente se utilizan para aplicaciones como luces intermitentes ( señales de giro ) y avisadores acústicos electrónicos , así como osciladores controlados por voltaje (VCO), inversores , fuentes de alimentación conmutadas , convertidores analógicos a digitales de doble pendiente y generadores de funciones .

El término oscilador de relajación , aunque se utiliza a menudo en ingeniería electrónica, también se aplica a sistemas dinámicos en muchas áreas diversas de la ciencia que producen oscilaciones no lineales y se pueden analizar utilizando el mismo modelo matemático que los osciladores de relajación electrónicos. ^{[8] [9] [10] [11] Por ejemplo,} los géiseres geotérmicos , ^{[12] [13]} las redes de células nerviosas en funcionamiento , ^[11] los sistemas de calefacción controlados por termostato , ^[14] las reacciones químicas acopladas, ^[9] el corazón humano que late, ^{[11] [14]} los terremotos, ^[12] el chirrido de la tiza en una pizarra, ^[14] las poblaciones cíclicas de animales depredadores y presas, y los sistemas de activación genética ^[9] se han modelado como osciladores de relajación. Las oscilaciones de relajación se caracterizan por dos procesos alternos en diferentes escalas de tiempo: un largo período de relajación durante el cual el sistema se acerca a un punto de equilibrio , alternando con un corto período impulsivo en el que el punto de equilibrio se desplaza. ^{[11] [12] [13] [15]} El período de un oscilador de relajación está determinado principalmente por la constante de tiempo de relajación . ^[11] Las oscilaciones de relajación son un tipo de ciclo límite y se estudian en la teoría de control no lineal . ^[16]

Osciladores electrónicos de relajación

Oscilador de relajación multivibrador Abraham-Bloch de tubo de vacío, Francia, 1920 (caja pequeña, izquierda) . Sus armónicos se utilizan para calibrar un medidor de ondas (centro) .

Oscilador multivibrador de tubo de vacío original de Abraham-Bloch, de su artículo de 1919

El primer circuito oscilador de relajación, el multivibrador astable , fue inventado por Henri Abraham y Eugene Bloch usando tubos de vacío durante la Primera Guerra Mundial . ^{[17] [18]} Balthasar van der Pol fue el primero en distinguir las oscilaciones de relajación de las oscilaciones armónicas, originó el término "oscilador de relajación" y derivó el primer modelo matemático de un oscilador de relajación, el influyente modelo de oscilador de Van der Pol , en 1920. ^{[18] [19] [20]} Van der Pol tomó prestado el término relajación de la mecánica; la descarga del condensador es análoga al proceso de relajación de la tensión , la desaparición gradual de la deformación y el retorno al equilibrio en un medio inelástico . ^[21] Los osciladores de relajación se pueden dividir en dos clases ^[13]

• Oscilador de diente de sierra, de barrido o de retorno : en este tipo, el condensador de almacenamiento de energía se carga lentamente pero se descarga rápidamente, prácticamente de forma instantánea, mediante un cortocircuito a través del dispositivo de conmutación. Por lo tanto, solo hay una "rampa" en la forma de onda de salida que ocupa prácticamente todo el período. El voltaje a través del condensador se aproxima a una onda de diente de sierra , mientras que la corriente a través del dispositivo de conmutación es una secuencia de pulsos cortos.
• Multivibrador astable : en este tipo, el condensador se carga y se descarga lentamente a través de una resistencia, por lo que la forma de onda de salida consta de dos partes, una rampa creciente y una rampa decreciente. El voltaje a través del condensador se aproxima a unaforma de onda triangular, mientras que la corriente a través del dispositivo de conmutación se aproxima a una onda cuadrada.

Antes de la llegada de la microelectrónica, los osciladores de relajación simples a menudo utilizaban un dispositivo de resistencia negativa con histéresis, como un tubo de tiratrón , ^[22] una lámpara de neón , ^[22] o un transistor unijuntura , sin embargo, hoy en día se construyen más a menudo con circuitos integrados dedicados, como el chip temporizador 555 .

Aplicaciones

Los osciladores de relajación se utilizan generalmente para producir señales de baja frecuencia para aplicaciones como luces parpadeantes y avisadores acústicos electrónicos. Durante la era de los tubos de vacío se utilizaron como osciladores en órganos electrónicos y circuitos de deflexión horizontal y bases de tiempo para osciloscopios CRT ; uno de los más comunes fue el circuito integrador Miller inventado por Alan Blumlein , que utilizaba tubos de vacío como fuente de corriente constante para producir una rampa muy lineal. ^[22] También se utilizan en osciladores controlados por voltaje (VCO), ^[23] inversores y fuentes de alimentación conmutadas , convertidores analógicos a digitales de doble pendiente y en generadores de funciones para producir ondas cuadradas y triangulares. Los osciladores de relajación se utilizan ampliamente porque son más fáciles de diseñar que los osciladores lineales, son más fáciles de fabricar en chips de circuitos integrados porque no requieren inductores como los osciladores LC, ^{[23] [24]} y se pueden sintonizar en un amplio rango de frecuencia. ^[24] Sin embargo, tienen más ruido de fase ^[23] y una estabilidad de frecuencia más pobre que los osciladores lineales. ^{[2] [23]}

Oscilador de Pearson-Anson

Diagrama de circuito de un oscilador de relajación capacitiva con un dispositivo de umbral de lámpara de neón

Este ejemplo se puede implementar con un circuito integrador capacitivo o resistivo-capacitivo accionado respectivamente por una fuente de corriente o voltaje constante , y un dispositivo de umbral con histéresis ( lámpara de neón , tiratrón , diac , transistor bipolar con polarización inversa , ^[25] o transistor unijuntura ) conectado en paralelo al capacitor. El capacitor se carga mediante la fuente de entrada, lo que hace que el voltaje a través del capacitor aumente. El dispositivo de umbral no conduce en absoluto hasta que el voltaje del capacitor alcanza su voltaje umbral (disparador). Luego aumenta considerablemente su conductancia de manera similar a una avalancha debido a la retroalimentación positiva inherente, que descarga rápidamente el capacitor. Cuando el voltaje a través del capacitor cae a un voltaje umbral inferior, el dispositivo deja de conducir y el capacitor comienza a cargarse nuevamente, y el ciclo se repite ad infinitum .

Si el elemento de umbral es una lámpara de neón , ^{[nb 1] [nb 2]} el circuito también proporciona un destello de luz con cada descarga del condensador. Este ejemplo de lámpara se muestra a continuación en el circuito típico utilizado para describir el efecto Pearson-Anson . La duración de la descarga se puede extender conectando una resistencia adicional en serie al elemento de umbral. Las dos resistencias forman un divisor de tensión; por lo tanto, la resistencia adicional debe tener una resistencia lo suficientemente baja como para alcanzar el umbral bajo.

Implementación alternativa con temporizador 555

Se puede construir un oscilador de relajación similar con un temporizador IC 555 (que actúa en modo astable) que reemplaza a la bombilla de neón anterior. Es decir, cuando un condensador elegido se carga a un valor de diseño (por ejemplo, 2/3 del voltaje de la fuente de alimentación), los comparadores dentro del temporizador 555 activan un interruptor de transistor que descarga gradualmente ese condensador a través de una resistencia elegida (que determina la constante de tiempo RC) a tierra. En el instante en que el condensador cae a un valor suficientemente bajo (por ejemplo, 1/3 del voltaje de la fuente de alimentación), el interruptor se activa para permitir que el condensador se cargue nuevamente. El diseño del comparador del popular 555 permite un funcionamiento preciso con cualquier suministro de 5 a 15 voltios o incluso más.

Otros osciladores que no sean comparadores pueden tener cambios de tiempo no deseados si cambia el voltaje de suministro.

Oscilador inductivo

Fundamento del oscilador de bloqueo de estado sólido

Un oscilador de bloqueo que utiliza las propiedades inductivas de un transformador de pulsos para generar ondas cuadradas impulsando el transformador hasta la saturación, lo que luego corta la corriente de suministro del transformador hasta que el transformador se descarga y se desatura, lo que luego activa otro pulso de corriente de suministro, generalmente utilizando un solo transistor como elemento de conmutación.

Oscilador de relajación basado en comparadores

Alternativamente, cuando el capacitor alcanza cada umbral, la fuente de carga puede cambiarse de la fuente de alimentación positiva a la fuente de alimentación negativa o viceversa. El ejemplo animado del disparador Schmitt inversor anterior funciona según el mismo principio (ya que el disparador Schmitt realiza la comparación internamente). En esta sección se analizará una implementación similar utilizando un comparador como componente discreto.

Un oscilador histerético basado en comparador.

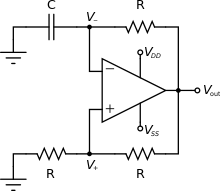
Este oscilador de relajación es un oscilador histerético, llamado así debido a la histéresis creada por el bucle de retroalimentación positiva implementado con el comparador (similar a un amplificador operacional ). Un circuito que implementa esta forma de conmutación histerética se conoce como disparador Schmitt . Por sí solo, el disparador es un multivibrador biestable . Sin embargo, la retroalimentación negativa lenta agregada al disparador por el circuito RC hace que el circuito oscile automáticamente. Es decir, la adición del circuito RC convierte al multivibrador biestable histerético en un multivibrador astable .

Concepto general

El sistema está en equilibrio inestable si tanto las entradas como las salidas del comparador están a cero voltios. En el momento en que cualquier tipo de ruido, ya sea térmico o electromagnético , hace que la salida del comparador supere el valor de cero (también es posible que la salida del comparador baje por debajo de cero, y se aplica un argumento similar al que sigue), la retroalimentación positiva en el comparador hace que la salida del comparador se sature en el riel positivo.

En otras palabras, debido a que la salida del comparador ahora es positiva, la entrada no inversora al comparador también es positiva y continúa aumentando a medida que aumenta la salida, debido al divisor de voltaje . Después de un breve tiempo, la salida del comparador es el riel de voltaje positivo, . ${\displaystyle V_{DD}}$

Circuito RC en serie

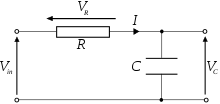
La entrada inversora y la salida del comparador están conectadas por un circuito RC en serie . Debido a esto, la entrada inversora del comparador se aproxima asintóticamente al voltaje de salida del comparador con una constante de tiempo RC. En el punto donde el voltaje en la entrada inversora es mayor que el de la entrada no inversora, la salida del comparador cae rápidamente debido a la retroalimentación positiva.

Esto se debe a que la entrada no inversora es menor que la entrada inversora y, a medida que la salida continúa disminuyendo, la diferencia entre las entradas se vuelve cada vez más negativa. Nuevamente, la entrada inversora se aproxima al voltaje de salida del comparador de manera asintótica y el ciclo se repite una vez que la entrada no inversora es mayor que la entrada inversora, por lo que el sistema oscila.

Ejemplo: Análisis de ecuaciones diferenciales de un oscilador de relajación basado en comparador

Análisis transitorio de un oscilador de relajación basado en comparador.

${\displaystyle \,\!V_{+}}$se establece a través de un divisor de voltaje resistivo : ${\displaystyle \,\!V_{\rm {out}}}$

${\displaystyle V_{+}={\frac {V_{\rm {out}}}{2}}}$

${\displaystyle \,\!V_{-}}$Se obtiene utilizando la ley de Ohm y la ecuación diferencial del condensador :

${\displaystyle {\frac {V_{\rm {out}}-V_{-}}{R}}=C{\frac {dV_{-}}{dt}}}$

Reorganizar la ecuación diferencial en su forma estándar da como resultado lo siguiente: ${\displaystyle \,\!V_{-}}$

${\displaystyle {\frac {dV_{-}}{dt}}+{\frac {V_{-}}{RC}}={\frac {V_{\rm {out}}}{RC}}}$

Observe que hay dos soluciones para la ecuación diferencial, la solución derivada o particular y la solución homogénea. Al calcular la solución derivada, observe que para esta forma particular, la solución es una constante. En otras palabras, donde A es una constante y . ${\displaystyle \,\!V_{-}=A}$ ${\displaystyle {\frac {dV_{-}}{dt}}=0}$

${\displaystyle {\frac {A}{RC}}={\frac {V_{\rm {out}}}{RC}}}$

${\displaystyle \,\!A=V_{\rm {out}}}$

Al utilizar la transformada de Laplace para resolver la ecuación homogénea se obtiene como resultado ${\displaystyle {\frac {dV_{-}}{dt}}+{\frac {V_{-}}{RC}}=0}$

${\displaystyle V_{-}=Be^{{\frac {-1}{RC}}t}}$

${\displaystyle \,\!V_{-}}$es la suma de la solución particular y homogénea.

${\displaystyle V_{-}=A+Be^{{\frac {-1}{RC}}t}}$

${\displaystyle V_{-}=V_{\rm {out}}+Be^{{\frac {-1}{RC}}t}}$

Para resolver B es necesario evaluar las condiciones iniciales. En el tiempo 0, y . Sustituyendo en nuestra ecuación anterior, ${\displaystyle V_{\rm {out}}=V_{dd}}$ ${\displaystyle \,\!V_{-}=0}$

${\displaystyle \,\!0=V_{dd}+B}$

${\displaystyle \,\!B=-V_{dd}}$

Frecuencia de oscilación

En primer lugar, supongamos que para facilitar el cálculo. Ignorando la carga inicial del condensador, que es irrelevante para los cálculos de la frecuencia, tenga en cuenta que las cargas y descargas oscilan entre y . Para el circuito anterior, V _ss debe ser menor que 0. La mitad del período (T) es el mismo que el tiempo que pasa de V _dd . Esto ocurre cuando V ₋ se carga de a . ${\displaystyle V_{dd}=-V_{ss}}$ ${\displaystyle {\frac {V_{dd}}{2}}}$ ${\displaystyle {\frac {V_{ss}}{2}}}$ ${\displaystyle V_{\rm {out}}}$ ${\displaystyle -{\frac {V_{dd}}{2}}}$ ${\displaystyle {\frac {V_{dd}}{2}}}$

${\displaystyle V_{-}=A+Be^{{\frac {-1}{RC}}t}}$

${\displaystyle {\frac {V_{dd}}{2}}=V_{dd}\left(1-{\frac {3}{2}}e^{{\frac {-1}{RC}}{\frac {T}{2}}}\right)}$

${\displaystyle {\frac {1}{3}}=e^{{\frac {-1}{RC}}{\frac {T}{2}}}}$

${\displaystyle \ln \left({\frac {1}{3}}\right)={\frac {-1}{RC}}{\frac {T}{2}}}$

${\displaystyle \,\!T=2\ln(3)RC}$

${\displaystyle \,\!f={\frac {1}{2\ln(3)RC}}}$

Cuando V _ss no es la inversa de V _dd, debemos preocuparnos por los tiempos de carga y descarga asimétricos. Teniendo esto en cuenta, obtenemos una fórmula de la forma:

${\displaystyle T=(RC)\left[\ln \left({\frac {2V_{ss}-V_{dd}}{V_{ss}}}\right)+\ln \left({\frac {2V_{dd}-V_{ss}}{V_{dd}}}\right)\right]}$

Lo cual se reduce al resultado anterior en el caso de que . ${\displaystyle V_{dd}=-V_{ss}}$

Véase también

• Multivibrador
• Modelo de FitzHugh-Nagumo  : un modelo histérico de, por ejemplo, una neurona.
• Disparador Schmitt  : circuito en el que se basa el oscilador de relajación basado en comparador.
• Transistor unijuntura  : Un transistor capaz de realizar oscilaciones de relajación.
• Robert Kearns  – Oscilador de relajación usado en disputa de patente de limpiaparabrisas intermitente.
• Ciclo límite  – Modelo matemático utilizado para analizar oscilaciones de relajación

Notas

1. Cuando se utiliza una lámpara de incandescencia catódica (de neón) o un tiratrón como dispositivos disparadores, a menudo se coloca una segunda resistencia con un valor de unas pocas decenas a cientos de ohmios en serie con el dispositivo disparador de gas para limitar la corriente del condensador de descarga y evitar que los electrodos de la lámpara se quemen rápidamente o que el revestimiento del cátodo del tiratrón se dañe por los pulsos repetidos de corriente intensa.
2. Los dispositivos de disparo con una tercera conexión de control, como el tiratrón o el transistor unijuntura, permiten sincronizar la descarga del condensador con un pulso de control. De este modo, la salida de diente de sierra se puede sincronizar con las señales producidas por otros elementos del circuito, ya que a menudo se utiliza como forma de onda de exploración para una pantalla, como un tubo de rayos catódicos .

Referencias

1. Graf, Rudolf F. (1999). Diccionario moderno de electrónica. Newnes. pág. 638. ISBN 0750698667.
2. Edson, William A. (1953). Osciladores de tubo de vacío (PDF) . Nueva York: John Wiley and Sons. pág. 3.en el sitio web Tubebooks de Peter Millet
3. Morris, Christopher G. Morris (1992). Diccionario académico de ciencia y tecnología. Gulf Professional Publishing. pág. 1829. ISBN 0122004000.
4. Du, Ke-Lin; MNS Swamy (2010). Sistemas de comunicación inalámbrica: desde subsistemas de RF hasta tecnologías habilitadoras 4G. Cambridge Univ. Press. p. 443. ISBN 978-1139485760.
5. Varigonda, Subbarao; Tryphon T. Georgiou (enero de 2001). "Dinámica de osciladores de relajación de relé" (PDF) . IEEE Transactions on Automatic Control . 46 (1). Inst. of Electrical and Electronic Engineers: 65. doi :10.1109/9.898696 . Consultado el 22 de febrero de 2014 .
6. Nave, Carl R. (2014). "Relaxation Oscillator Concept". HyperPhysics . Departamento de Física y Astronomía, Universidad Estatal de Georgia . Consultado el 22 de febrero de 2014 .
7. Oliveira, Luis B.; et al. (2008). Análisis y diseño de osciladores en cuadratura. Springer. p. 24. ISBN 978-1402085161.
8. DeLiang, Wang (1999). "Osciladores y redes de relajación" (PDF) . Wiley Encyclopedia of Electrical and Electronics Engineering, vol. 18. Wiley & Sons. págs. 396–405 . Consultado el 2 de febrero de 2014 .
9. Sauro, Herbert M. (2009). "Circuitos oscilatorios" (PDF) . Apuntes de clase sobre osciladores: sistemas y biología sintética . Laboratorio Sauro, Centro de Biología Sintética, Universidad de Washington . Consultado el 12 de noviembre de 2019 .,
10. Letellier, Christopher (2013). Caos en la naturaleza. World Scientific. págs. 132-133. ISBN 978-9814374422.
11. Ginoux, Jean-Marc; Letellier, Christophe (junio de 2012). "Van der Pol y la historia de las oscilaciones de relajación: hacia la emergencia de un concepto". Chaos . 22 (2): 023120. arXiv : 1408.4890 . Bibcode :2012Chaos..22b3120G. doi :10.1063/1.3670008. PMID  22757527. S2CID  293369 . Consultado el 24 de diciembre de 2014 .
12. Enns, Richard H.; George C. McGuire (2001). Física no lineal con Mathematica para científicos e ingenieros. Springer. pág. 277. ISBN 0817642234.
13. Pippard, AB (2007). La física de la vibración. Cambridge Univ. Press. pp. 359–361. ISBN 978-0521033336.
14. Pippard, La física de la vibración, pág. 41-42
15. Kinoshita, Shuichi (2013). "Introducción a los fenómenos de no equilibrio". Formaciones de patrones y fenómenos oscilatorios . Newnes. pág. 17. ISBN 978-0123972996. Recuperado el 24 de febrero de 2014 .
16. Véase el capítulo 9, "Ciclos límite y oscilaciones de relajación" en Leigh, James R. (1983). Fundamentos de la teoría de control no lineal. Instituto de Ingenieros Eléctricos. Págs. 66-70. ISBN. 0906048966.
17. Abraham, H.; E. Bloch (1919). "Mesure en valeur absolue des périodes des oscilations électriques de haute fréquence (Medición de los períodos de oscilaciones eléctricas de alta frecuencia)" (PDF) . Anales de Física . 9 (1). París: Société Française de Physique: 237–302. doi :10.1051/jphystap:019190090021100.
18. Ginoux, Jean-Marc (2012). "Van der Pol y la historia de las oscilaciones de relajación: Hacia el surgimiento de un concepto". Chaos: An Interdisciplinary Journal of Nonlinear Science . 22 (2). Chaos 22 (2012) 023120: 023120. arXiv : 1408.4890 . Bibcode :2012Chaos..22b3120G. doi :10.1063/1.3670008. PMID  22757527. S2CID  293369.
19. van der Pol, B. (1920). "Una teoría de la amplitud de las vibraciones libres y forzadas de triodo". Radio Review . 1 : 701–710, 754–762.
20. van der Pol, Balthasar (1926). "Sobre las oscilaciones de relajación". The London, Edinburgh, and Dublin Philosophical Magazine 2 . 2 : 978–992. doi :10.1080/14786442608564127.
21. Shukla, Jai Karan N. (1965). "Teoría discontinua de osciladores de relajación". Tesis de maestría en ciencias. Departamento de Ingeniería Eléctrica, Universidad Estatal de Kansas . Consultado el 23 de febrero de 2014 . {{cite journal}}: Requiere citar revista |journal=( ayuda )
22. Puckle, OS (1951). Bases de tiempo (generadores de escaneo), 2.ª ed. Londres: Chapman and Hall, Ltd., págs. 15-27.
23. Abidi, Assad A.; Robert J. Meyer (1996). "Ruido en osciladores de relajación". Circuitos de recuperación de reloj y bucles de enganche de fase monolíticos: teoría y diseño . John Wiley and Sons. pág. 182. ISBN 9780780311497. Recuperado el 22 de septiembre de 2015 .
24. van der Tang, J.; Kasperkovitz, Dieter; van Roermund, Arthur HM (2006). Diseño de oscilador de alta frecuencia para transceptores integrados. Springer. p. 12. ISBN 0306487160.
25. "Comunicaciones Shaw".