Gravedad de Marte

Fuerza gravitacional ejercida por el planeta Marte

Gravedad de la Tierra , Marte y la Luna en la elevación

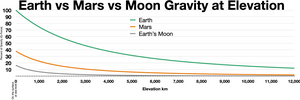
La gravedad de Marte es un fenómeno natural, debido a la ley de la gravedad , o gravitación, por la cual todas las cosas con masa alrededor del planeta Marte son atraídas hacia él. Es más débil que la gravedad de la Tierra debido a la menor masa del planeta. La aceleración gravitatoria promedio en Marte es de 3,72076 m/s2 ⁽ aproximadamente el 38% de la gravedad de la Tierra ) y varía. ^[1]

En general, la isostasia controlada por la topografía impulsa las anomalías de gravedad del aire libre de longitud de onda corta . ^[2] Al mismo tiempo, el flujo convectivo y la fuerza finita del manto conducen a anomalías de gravedad del aire libre a escala planetaria de longitud de onda larga en todo el planeta. ^{[3] [4]} La variación en el espesor de la corteza, las actividades magmáticas y volcánicas, el levantamiento de Moho inducido por el impacto , la variación estacional de los casquetes polares, la variación de la masa atmosférica y la variación de la porosidad de la corteza también podrían correlacionarse con las variaciones laterales. ^{[5] [6] [7] [8] [9]}

A lo largo de los años se han elaborado modelos que consisten en un número cada vez mayor pero limitado de armónicos esféricos . Los mapas producidos han incluido la anomalía de gravedad en aire libre , la anomalía de gravedad de Bouguer y el espesor de la corteza. En algunas áreas de Marte existe una correlación entre las anomalías de gravedad y la topografía. Dada la topografía conocida, se puede inferir un campo de gravedad de mayor resolución. La deformación de marea de Marte por el Sol o Fobos se puede medir por su gravedad. Esto revela cuán rígido es el interior y muestra que el núcleo es parcialmente líquido. Por lo tanto, el estudio de la gravedad de la superficie de Marte puede brindar información sobre diferentes características y proporcionar información útil para futuros aterrizajes en Marte .

Medición

Armónico esférico rotatorio, con para la vertical y para la horizontal. Para el C ₂₀ y C ₃₀ marcianos , varían con el tiempo debido a la variación estacional de la masa de los casquetes polares a través del ciclo anual de sublimación-condensación del dióxido de carbono. ${\displaystyle \ell =0{\text{ to }}4}$ ${\displaystyle m=0{\text{ to }}4}$

Para comprender la gravedad de Marte, a menudo se miden su fuerza de campo gravitatorio g y su potencial gravitatorio U. En términos simples, si se supone que Marte es un cuerpo estático perfectamente esférico de radio R _M , siempre que haya un solo satélite girando alrededor de Marte en una órbita circular y dicha interacción gravitatoria sea la única fuerza que actúe en el sistema, la ecuación sería

${\displaystyle {\frac {GMm}{r^{2}}}=mr\omega ^{2},}$

donde G es la constante universal de gravitación (comúnmente tomada como G = 6,674 × 10 ⁻¹¹ m ³ kg ⁻¹ s ⁻² ), ^[10] M es la masa de Marte (valor más actualizado: 6,41693 × 10 ²³ kg), ^[11] m es la masa del satélite, r es la distancia entre Marte y el satélite, y es la velocidad angular del satélite, que también es equivalente a ( T es el período orbital del satélite). ${\displaystyle \omega }$ ${\displaystyle {\frac {2\pi }{T}}}$

Por lo tanto, , donde R _M es el radio de Marte. Con una medición adecuada, r , T y R _M son parámetros que se pueden obtener desde la Tierra. ${\displaystyle g={\frac {GM}{R_{M}^{2}}}={\frac {r^{3}\omega ^{2}}{R_{M}^{2}}}={\frac {4r^{3}\pi ^{2}}{T^{2}R_{M}^{2}}}}$

Sin embargo, como Marte es un cuerpo planetario genérico, no esférico e influenciado por procesos geológicos complejos, con mayor precisión, el potencial gravitacional se describe con funciones armónicas esféricas , siguiendo la convención en geodesia; ver modelo geopotencial .

${\displaystyle U(r,\lambda ,\psi )=-{\frac {GM}{r}}\left(1+\sum _{\ell =2}^{\ell =L}\left({\frac {R}{r}}\right)^{\ell }\left(C_{\ell 0}P_{\ell }^{0}(\sin \psi )+\sum _{m=1}^{+\ell }(C_{\ell m}\cos m\lambda +S_{\ell m}\sin m\lambda )P_{\ell }^{m}(\sin \psi )\right)\right),}$^[12]

donde son las coordenadas esféricas del punto de prueba. ^[12] es la longitud y es la latitud. y son coeficientes armónicos adimensionales de grado y orden . ^[12] es el polinomio de Legendre de grado con y es el polinomio de Legendre asociado con . Estos se utilizan para describir soluciones de la ecuación de Laplace . ^[12] es el radio medio del planeta. ^[12] El coeficiente a veces se escribe como . ${\displaystyle r,\psi ,\lambda }$ ${\displaystyle \lambda }$ ${\displaystyle \psi }$ ${\displaystyle C_{\ell m}}$ ${\displaystyle S_{\ell m}}$ ${\displaystyle l}$ ${\displaystyle m}$ ${\displaystyle P_{\ell }^{m}}$ ${\displaystyle l}$ ${\displaystyle m=0}$ ${\displaystyle m>0}$ ${\displaystyle R}$ ${\displaystyle C_{\ell 0}}$ ${\displaystyle J_{n}}$

1. Cuanto menor sea el grado y el orden , mayor será la longitud de onda de la anomalía que representa. A su vez, la anomalía gravitacional de longitud de onda larga está influenciada por las estructuras geofísicas globales. ${\displaystyle \ell }$ ${\displaystyle m}$
2. Cuanto mayor sea el grado y el orden , menor será la longitud de onda de la anomalía que representa. Para grados superiores a 50, se ha demostrado que esas variaciones tienen una alta correlación con la topografía. ^[13] La interpretación geofísica de las características de la superficie podría ayudar a obtener una imagen más completa del campo gravitatorio marciano, aunque podrían producirse resultados engañosos. ^[13] ${\displaystyle \ell }$ ${\displaystyle m}$

La técnica más antigua para determinar la gravedad de Marte es la observación desde la Tierra. Más tarde, con la llegada de naves espaciales no tripuladas, se desarrollaron modelos de gravedad posteriores a partir de datos de seguimiento por radio.

Los científicos midieron la perturbación de diferentes naves espaciales a través de métodos Doppler y de seguimiento de distancia para desarrollar diferentes modelos de gravedad desde la primera llegada de la sonda espacial no tripulada Mariner 9 en 1971. (Crédito: Estudio de visualización científica de la NASA)

Observación desde la Tierra

Antes de la llegada de las sondas espaciales Mariner 9 y Viking a Marte, solo se disponía de una estimación de la constante gravitacional marciana GM, es decir, la constante universal de gravitación multiplicada por la masa de Marte, para deducir las propiedades del campo gravitacional marciano. ^[14] La GM se podía obtener mediante observaciones de los movimientos de los satélites naturales de Marte ( Fobos y Deimos ) y sobrevuelos de sondas espaciales sobre Marte ( Mariner 4 y Mariner 6 ). ^[14]

Las observaciones a largo plazo desde la Tierra de los movimientos de Fobos y Deimos proporcionan parámetros físicos que incluyen el semieje mayor , la excentricidad , el ángulo de inclinación respecto del plano laplaciano , etc., ^[15] que permiten calcular la relación entre la masa solar y la masa de Marte, el momento de inercia y el coeficiente del potencial gravitacional de Marte, y dan estimaciones iniciales del campo gravitacional de Marte. ^[15]

Inferido a partir de datos de seguimiento por radio

Doppler de tres vías, con transmisor y receptor de señal separados

El seguimiento preciso de las naves espaciales es de suma importancia para la modelización precisa de la gravedad, ya que los modelos de gravedad se desarrollan a partir de la observación de pequeñas perturbaciones de las naves espaciales, es decir, pequeñas variaciones en la velocidad y la altitud. El seguimiento se realiza básicamente mediante las antenas de la Red de Espacio Profundo (DSN), con seguimiento Doppler y de rango unidireccional, bidireccional y tridireccional aplicado. ^[16] El seguimiento unidireccional significa que los datos se transmiten de una manera a la DSN desde la nave espacial, mientras que el bidireccional y el tridireccional implican la transmisión de señales desde la Tierra a la nave espacial (enlace ascendente) y, a partir de entonces, se transponen de manera coherente de regreso a la Tierra (enlace descendente). ^[16] La diferencia entre el seguimiento bidireccional y el tridireccional es que el primero tiene el mismo transmisor y receptor de señales en la Tierra, mientras que el segundo tiene el transmisor y el receptor en diferentes ubicaciones en la Tierra. ^[16] El uso de estos tres tipos de datos de seguimiento mejora la cobertura y la calidad de los datos, ya que uno podría llenar el vacío de datos de otro. ^[16]

El seguimiento Doppler es una técnica común para el seguimiento de naves espaciales, que utiliza el método de velocidad radial, que implica la detección de los cambios Doppler. ^[13] A medida que la nave espacial se aleja de nosotros a lo largo de la línea de visión, se produciría un desplazamiento hacia el rojo de la señal, mientras que, en sentido inverso, se produciría un desplazamiento hacia el azul de la señal. Esta técnica también se ha aplicado para la observación del movimiento de exoplanetas. ^[17] Mientras que para el seguimiento de distancia, se realiza a través de la medición del tiempo de propagación de ida y vuelta de la señal. ^[13] La combinación del desplazamiento Doppler y la observación de distancia promueve una mayor precisión de seguimiento de la nave espacial.

Los datos de seguimiento se convertirían entonces para desarrollar modelos de gravedad global utilizando la ecuación armónica esférica que se muestra arriba. Sin embargo, se deben eliminar aún más los efectos debidos al efecto de la marea sólida , varios efectos relativistas debidos al Sol, Júpiter y Saturno, fuerzas no conservativas (por ejemplo, desaturaciones del momento angular (AMD), arrastre atmosférico y presión de radiación solar ) ^[13] , de lo contrario, se producen errores considerables.

Historia

El último modelo de gravedad para Marte es el Goddard Mars Model 3 (GMM-3), producido en 2016, con una solución de armónicos esféricos hasta el grado y orden 120. ^[13] Este modelo se desarrolló a partir de 16 años de datos de seguimiento de radio de Mars Global Surveyor (MGS), Mars Odyssey y Mars Reconnaissance Orbiter (MRO), así como el modelo de topografía MOLA y proporciona una resolución global de 115 km. ^[13] Junto con este modelo se produjo un mapa de anomalías de gravedad en aire libre, un mapa de anomalías de gravedad de Bouguer y un mapa del espesor de la corteza. ^[13] En comparación con MRO110C y otros modelos anteriores, la mejora principal de la estimación del campo de gravedad proviene de un modelado más cuidadoso de las fuerzas no conservativas aplicadas a la nave espacial. ^[13]

Las técnicas de seguimiento de la nave espacial y la interpretación geofísica de las características de la superficie pueden afectar la resolución de la fuerza del campo gravitatorio. La mejor técnica favorece las soluciones armónicas esféricas a grados y órdenes más altos. El análisis independiente de los datos de seguimiento de Mariner 9 y Viking Orbiter arrojó una solución armónica esférica de grado y orden 6., ^[18] Una combinación adicional de los dos conjuntos de datos, junto con la correlación de anomalías con características volcánicas (anomalía positiva) y depresión impresa profunda (anomalía negativa) asistida por datos de imagen permite producir una solución armónica esférica de grado y orden 18. ^[19] El uso adicional del método de restricción a priori espacial, que había tenido en cuenta la topografía para resolver la restricción de la ley de potencia de Kaula, había favorecido el modelo de hasta grado 50 de solución armónica esférica en resolución global (Goddard Mars Model-1, o GMM-1) ^[20] luego los modelos posteriores con mayor completitud y grado y orden hasta 120 para el último GMM-3. ^[13]

Mapa de gravedad en aire libre de Marte elaborado junto con la solución de gravedad GMM-3 ^[13] (Rojo: gravedad alta; Azul: gravedad baja) (Crédito: Estudio de visualización científica de la NASA)

Por lo tanto, en la actualidad los modelos de gravedad no se producen directamente mediante la transferencia de los datos de gravedad medidos a ningún sistema de información espacial porque es difícil producir modelos con una resolución suficientemente alta. Los datos topográficos obtenidos del instrumento MOLA a bordo de la Mars Global Surveyor se convierten así en una herramienta útil para producir un modelo de gravedad a escala corta más detallado, utilizando la correlación gravedad-topografía en longitudes de onda cortas. ^[13] Sin embargo, no todas las regiones de Marte muestran dicha correlación, en particular las tierras bajas del norte y los polos. ^[13] Se podrían producir fácilmente resultados engañosos, lo que podría conducir a una interpretación geofísica incorrecta. ^[13]

Las modificaciones posteriores del modelo de gravedad incluyen tener en cuenta otras fuerzas no conservativas que actúan sobre las naves espaciales, incluyendo la resistencia atmosférica , la presión de la radiación solar , la presión de la radiación solar reflejada de Marte , la emisión térmica de Marte y el empuje de la nave espacial que desgira o desatura las ruedas de momento angular . ^[14] Además, la precesión marciana y la atracción del tercer cuerpo debido al Sol , la Luna y los planetas, que podrían afectar la órbita de la nave espacial, así como los efectos relavísticos en las mediciones, también deberían corregirse. ^[7] Estos factores podrían llevar a un desplazamiento del campo de gravedad real. Por lo tanto, se requiere un modelado preciso para eliminar el desplazamiento. Dicho trabajo aún está en curso.

Campo de gravedad estático

Muchos investigadores han señalado la correlación entre las anomalías de gravedad en aire libre de longitud de onda corta (que varían localmente) y la topografía. Para las regiones con una correlación más alta, las anomalías de gravedad en aire libre podrían expandirse a un grado más alto de fuerza a través de la interpretación geofísica de las características de la superficie, ^[13] de modo que el mapa de gravedad podría ofrecer una mayor resolución. Se ha descubierto que las tierras altas del sur tienen una alta correlación gravedad/topografía, pero no para las tierras bajas del norte. ^[13] Por lo tanto, la resolución del modelo de anomalía de gravedad en aire libre generalmente tiene una resolución más alta para el hemisferio sur, tan alta como más de 100 km. ^[13]

Las anomalías de gravedad en aire libre son relativamente más fáciles de medir que las anomalías de Bouguer siempre que se disponga de datos topográficos porque no es necesario eliminar el efecto gravitacional debido al efecto del exceso o déficit de masa del terreno después de que la gravedad se reduce al nivel del mar. Sin embargo, para interpretar la estructura de la corteza, es necesaria una mayor eliminación de dicho efecto gravitacional, de modo que la gravedad reducida solo sea el resultado del núcleo, el manto y la corteza debajo del dato. ^[5] El producto después de la eliminación son las anomalías de Bouguer. Sin embargo, la densidad del material en la construcción del terreno sería la restricción más importante en el cálculo, que puede variar lateralmente en el planeta y se ve afectada por la porosidad y la geoquímica de la roca. ^{[5] [9]} Se podría obtener información relevante de los meteoritos marcianos y el análisis in situ.

Anomalías de gravedad local

La variación del límite entre la corteza y el manto, la intrusión, el vulcanismo y la topografía pueden afectar la órbita de las naves espaciales, debido a la mayor densidad del manto y del material volcánico y a la menor densidad de la corteza. (No está en escala) +ve: anomalía positiva; -ve: anomalía negativa

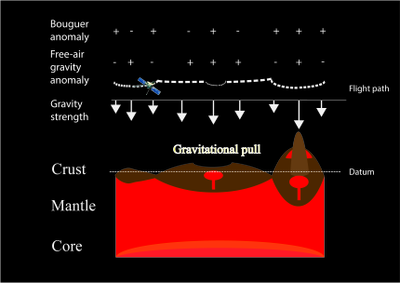
Dado que las anomalías de gravedad de Bouguer tienen fuertes vínculos con la profundidad del límite entre la corteza y el manto, una anomalía de Bouguer positiva puede significar que tiene una corteza más delgada compuesta de material de menor densidad y está influenciada más fuertemente por el manto más denso, y viceversa. Sin embargo, también podría deberse a la diferencia en densidad de la carga volcánica erupcionada y la carga sedimentaria, así como a la intrusión y remoción de material del subsuelo. ^{[5] [6] [25]} Muchas de estas anomalías están asociadas con características geológicas o topográficas. ^[5] Unas pocas excepciones incluyen la anomalía 63°E, 71°N, ^[5] que puede representar una extensa estructura enterrada de más de 600 km de tamaño, anterior a la superficie enterrada del Noéico temprano. ^[5]

Anomalías topográficas

Se ha demostrado una fuerte correlación entre la topografía y las anomalías de gravedad en aire libre de longitud de onda corta tanto para el estudio del campo gravitatorio de la Tierra como de la Luna, ^[2] y puede explicarse por la amplia ocurrencia de isostasia. ^{[2] [26]} Se espera una alta correlación para el grado superior a 50 (anomalía de longitud de onda corta) en Marte. ^[13] Y podría ser tan alta como 0,9 para los grados entre 70 y 85. ^[13] Dicha correlación podría explicarse por la compensación flexural de las cargas topográficas. ^{[2] [26]} Se observa que las regiones más antiguas de Marte están compensadas isostáticamente mientras que las regiones más jóvenes suelen estar solo parcialmente compensadas. ^[13]

Anomalías de construcciones volcánicas

Mapa de gravedad de Bouguer en Marte, elaborado junto con la solución de gravedad GMM-3 en 2016 ^[13] (Rojo: gravedad alta; Azul: gravedad baja) (Crédito: Estudio de visualización científica de la NASA)

Diferentes construcciones volcánicas podrían comportarse de manera diferente en términos de anomalías gravitacionales. Los volcanes Olympus Mons y Tharsis Montes producen las anomalías gravitacionales positivas en aire libre más pequeñas del sistema solar. ^{[5] Sin embargo,} Alba Patera , también una elevación volcánica, al norte de Tharsis Montes , produce una anomalía Bouguer negativa, aunque su extensión es similar a la de Olympus Mons. ^[5] Y en el caso de Elysium Mons , se ha descubierto que su centro tiene un ligero aumento de las anomalías Bouguer en un contexto general de anomalía negativa amplia en la elevación Elysium. [ ^5]

El conocimiento de la anomalía de los volcanes, junto con la densidad del material volcánico, sería útil para determinar la composición litosférica y la evolución de la corteza de diferentes edificios volcánicos. ^[27] Se ha sugerido que la lava extruida podría variar de andesita (baja densidad) a basáltica (alta densidad) y la composición podría cambiar durante la construcción del escudo volcánico, lo que contribuye a la anomalía. ^[27] Otro escenario es que es posible que el material de alta densidad se haya introducido debajo del volcán. ^{[27] [6] Tal configuración ya se ha observado sobre la famosa Syrtis major, que se ha inferido que tiene una} cámara de magma extinta con 3300 kg m ³ debajo del volcán, evidente a partir de la anomalía positiva de Bouguer. ^[6]

Anomalías de las depresiones

Las diferentes depresiones también se comportan de manera diferente en la anomalía de Bouguer. Las cuencas de impacto gigantes como las de Argyre , Isidis , Hellas y Utopia también exhiben anomalías positivas de Bouguer muy fuertes de manera circular. ^[5] Se ha debatido sobre el origen de estas cuencas en cráteres de impacto. Si es así, las anomalías positivas pueden deberse al levantamiento de Moho, al adelgazamiento de la corteza y a eventos de modificación por cargas superficiales sedimentarias y volcánicas después del impacto. ^{[5] [25]}

Pero al mismo tiempo también hay algunas grandes cuencas que no están asociadas con tal anomalía positiva de Bouguer, por ejemplo, Daedalia , el norte de Tharsis y Elysium , que se cree que están sustentadas por la llanura de tierras bajas del norte . ^[5]

Además, también se ha descubierto que ciertas partes de Coprates , Eos Chasma y Kasei Valles tienen anomalías de Bouguer positivas, ^[5] aunque son depresiones topográficas. Esto puede sugerir que estas depresiones están sustentadas por un cuerpo de intrusión denso y poco profundo. ^[5]

Anomalías de gravedad global

Las anomalías gravitacionales globales, también denominadas anomalías gravitacionales de longitud de onda larga, son los armónicos de bajo grado del campo gravitacional, ^[4] que no pueden atribuirse a la isostasia local, sino más bien a la fuerza finita del manto y a las diferencias de densidad en la corriente de convección. ^{[13] [3] [4]} Para Marte, el componente más grande de la anomalía de Bouguer es el armónico de grado uno, que representa el déficit de masa en el hemisferio sur y el exceso en el hemisferio norte. ^[5] El segundo componente más grande corresponde al aplanamiento del planeta y al abultamiento de Tharsis . ^[5]

Los primeros estudios del geoide en los años 1950 y 1960 se han centrado en los armónicos de bajo grado del campo gravitatorio de la Tierra para comprender su estructura interior. ^[4] Se ha sugerido que tales anomalías de longitud de onda larga en la Tierra podrían ser contribuidas por las fuentes ubicadas en el manto profundo y no en la corteza, por ejemplo, causadas por las diferencias de densidad en el impulso de la corriente de convección , ^{[4] [28]} que ha estado evolucionando con el tiempo. La correlación entre ciertas anomalías topográficas y anomalías de gravedad de longitud de onda larga, por ejemplo, la dorsal mesoatlántica y la dorsal de Carlsberg , que son topográficamente altas y gravitatoriamente altas en el fondo del océano, se convirtió así en el argumento para la idea de la corriente de convección en la Tierra en los años 1970, ^{[29] [30]} aunque tales correlaciones son débiles en el panorama global.

Otra posible explicación para las anomalías a escala global es la fuerza finita del manto (en contraste con el estrés cero), que hace que la gravedad se desvíe del equilibrio hidrostático . ^[3] Para esta teoría, debido a la fuerza finita, el flujo puede no existir para la mayoría de las regiones que están subestresadas. ^[3] Y las variaciones de densidad del manto profundo podrían ser el resultado de inhomogeneidades químicas asociadas con las separaciones de los continentes, ^[3] y las cicatrices dejadas en la Tierra después del desprendimiento de la luna. ^[3] Estos son los casos sugeridos para funcionar cuando se permite que ocurra un flujo lento en ciertas circunstancias. ^[3] Sin embargo, se ha argumentado que la teoría puede no ser físicamente factible. ^[4]

Campo de gravedad variable en el tiempo

En Marte se produce un ciclo de sublimación-condensación que da lugar a un intercambio de dióxido de carbono entre la criosfera y la atmósfera. A su vez, se produce un intercambio de masa entre las dos esferas, lo que da lugar a una variación estacional de la gravedad. (Cortesía de la NASA/JPL-Caltech)

Cambio estacional del campo gravitatorio en los polos

El ciclo de sublimación - condensación del dióxido de carbono en Marte entre la atmósfera y la criosfera (capa de hielo polar) opera estacionalmente. ^[8] Este ciclo contribuye como casi la única variable que explica los cambios en el campo gravitacional en Marte. ^[8] El potencial gravitacional de Marte medido desde los orbitadores podría generalizarse como la ecuación siguiente:

${\displaystyle V({\text{Mars}})=V({\text{solid planet}})+V({\text{seasonal caps}}+{\text{atmosphere}})}$^[8]

A su vez, cuando hay más masa en los casquetes estacionales debido a la mayor condensación de dióxido de carbono de la atmósfera, la masa de la atmósfera disminuiría. Tienen una relación inversa entre sí. Y el cambio de masa tiene un efecto directo sobre el potencial gravitatorio medido.

El intercambio de masa estacional entre el casquete polar norte y el casquete polar sur exhibe una variación de gravedad de longitud de onda larga con el tiempo. ^{[8] [13]} Largos años de observación continua han encontrado que la determinación del coeficiente de gravedad normalizado zonal par C _{l = 2, m = 0} y el coeficiente de gravedad normalizado zonal impar C _{l = 3, m = 0} son cruciales para delinear la gravedad variable en el tiempo debido a dicho intercambio de masa, ^{[24] [8] [31] [32]} donde es el grado mientras que es el orden. Más comúnmente, se representan en forma de C _lm en artículos de investigación. ${\displaystyle l}$ ${\displaystyle m}$

Si consideramos los dos polos como dos masas puntuales distintas, entonces, sus masas se definen como,

${\displaystyle M_{NP}={\frac {C_{20}+C_{30}}{2}}\,M_{\text{Mars}}}$^[32]

${\displaystyle M_{SP}={\frac {C_{20}-C_{30}}{2}}\,M_{\text{Mars}}}$^[32]

Los datos han indicado que la variación máxima de masa del casquete polar sur es de aproximadamente 8,4 × 10 ¹⁵ kg, ^[13] y se produce cerca del equinoccio de otoño , ^[13] mientras que la del polo norte es de aproximadamente 6,2 × 10 ¹⁵ kg, ^[13] y se produce entre el solsticio de invierno y el equinoccio de primavera . ^[13]

Hablando a largo plazo, se ha descubierto que la masa de hielo almacenada en el Polo Norte aumentaría en (1,4 ± 0,5) × 10 ¹¹ kg, ^[8] mientras que en el Polo Sur disminuiría en (0,8 ± 0,6) × 10 ¹¹ kg. ^[8] Además, la atmósfera habría disminuido en términos de la masa de dióxido de carbono en (0,6 ± 0,6) × 10 ¹¹ kg también a largo plazo. ^[8] Debido a la existencia de incertidumbres, no está claro si la migración de material desde el Polo Sur al Polo Norte está en curso, aunque tal posibilidad no se puede descartar. ^[8]

Marea

Las dos principales fuerzas de marea que actúan sobre Marte son la marea solar y la marea de Fobos. ^[13] _El número de Love k2 es una constante proporcional adimensional importante que relaciona el campo de marea que actúa sobre el cuerpo con el momento multipolar resultante de la distribución de masa del cuerpo. Por lo general, k2 _puede indicar una deformación cuadrupolar. ^[13] Encontrar k2 _es útil para comprender la estructura interior de Marte. ^[13] El k2 más actualizado _obtenido por el equipo de Genova es 0,1697 ± 0,0009. ^[13] Como si k2 _fuera menor que 0,10, se indicaría un núcleo sólido, esto indica que al menos el núcleo externo es líquido en Marte, ^[31] y el radio del núcleo predicho es de 1520-1840 km. ^[31]

Sin embargo, los datos actuales de seguimiento de radio de MGS, ODY y MRO no permiten detectar el efecto del desfase de fase en las mareas porque es demasiado débil y se necesita una medición más precisa de la perturbación de las naves espaciales en el futuro. ^[13]

Implicaciones geofísicas

Espesor de la corteza

Histograma del porcentaje de área frente al espesor de la corteza de Marte: 32 km y 58 km son los dos picos principales del histograma.

Comparación de topografía , anomalía de gravedad en aire libre y mapa de densidad de la corteza – Rojo: gravedad alta; Azul: gravedad baja

Actualmente no se dispone de una medición directa del espesor de la corteza de Marte. Las implicaciones geoquímicas de los meteoritos SNC y del meteorito de ortopiroxenita ALH84001 sugirieron que el espesor medio de la corteza de Marte es de 100 a 250 km. ^[33] El análisis de relajación viscosa sugirió que el espesor máximo es de 50 a 100 km. Este espesor es fundamental para mantener las variaciones hemisféricas de la corteza y evitar el flujo en canal. ^[34] Los estudios combinados de geofísica y geoquímica sugirieron que el espesor medio de la corteza podría ser de hasta 50 ± 12 km. ^[35]

La medición del campo gravitatorio mediante diferentes orbitadores permite producir un modelo de potencial de Bouguer global de mayor resolución. ^[5] Al eliminar las anomalías de densidad superficial local y el efecto del aplanamiento del núcleo, ^[5] se produce el potencial de Bouguer residual, como lo indica la siguiente ecuación:

${\displaystyle U_{RB}=U_{B}-U_{\text{core}}-U_{\text{local}}}$^[5]

El potencial residual de Bouguer es aportado por el manto. ^[5] La ondulación del límite corteza-manto, o la superficie de Moho , con la masa del terreno corregida, debería haber dado lugar a una anomalía residual variable. ^[5] A su vez, si se observa un límite ondulado, debería haber cambios en el espesor de la corteza.

Un estudio global de los datos residuales de la anomalía de Bouguer indica que el espesor de la corteza de Marte varía de 5,8 km a 102 km. ^[5] Se identifican dos picos principales a 32 km y 58 km a partir de un histograma de áreas iguales del espesor de la corteza. ^[5] Estos dos picos están vinculados a la dicotomía de la corteza de Marte. ^[5] Casi toda la corteza más gruesa de 60 km es aportada por las tierras altas del sur, con un espesor generalmente uniforme. ^[5] Y las tierras bajas del norte en general tienen una corteza más delgada. Se ha descubierto que el espesor de la corteza de la región Arabia Terra y del hemisferio norte depende de la latitud. ^[5] Cuanto más al sur hacia Sinai Planum y Lunae Planum , más engrosada es la corteza. ^[5]

Entre todas las regiones, Thaumasia y Claritis contienen la porción más gruesa de corteza en Marte, lo que explica el histograma > 70 km. ^[5] Se observa que las cuencas Hellas y Argyre tienen una corteza más delgada que 30 km, ^[5] que son el área excepcionalmente delgada en el hemisferio sur. ^{[5] También se observa que} Isidis y Utopia tienen un adelgazamiento significativo de la corteza, ^[5] y se cree que el centro de las cuencas de Isidis tiene la corteza más delgada en Marte. ^[5]

Redistribución de la corteza por impacto y relajación viscosa

Después del impacto inicial, un alto flujo de calor y un alto contenido de agua habrían favorecido la relajación viscosa. La corteza se vuelve más dúctil. La topografía de la cuenca de los cráteres está, por tanto, sujeta a un mayor estrés debido a la autogravitación, que impulsa aún más el flujo de la corteza y la descomposición del relieve. Sin embargo, este análisis puede no funcionar para cráteres de impacto gigantes como las cuencas Hellas , Utopia , Argyre e Isidis . ^[25]

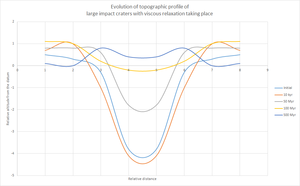
Se cree que se produjo un adelgazamiento de la corteza debajo de casi todos los principales cráteres de impacto. ^[5] Las posibles causas son la excavación de la corteza, la modificación a través del emplazamiento de material volcánico y el flujo de la corteza que tuvo lugar en la litosfera débil. ^[5] Con la corteza anterior al impacto excavada, se produciría una restauración gravitacional a través del levantamiento del manto central, de modo que el déficit de masa de la cavidad podría compensarse con la masa del material más denso levantado. ^[5]

Las cuencas de impacto gigantes Utopia, Hellas, Argyre e Isidis son algunos de los ejemplos más destacados. ^[5] Utopia , una cuenca de impacto ubicada en las tierras bajas del norte, está llena de material sedimentario ligero y depositado por agua y tiene una corteza ligeramente engrosada en el centro. ^[5] Esto se debe potencialmente a un gran proceso de renovación de la superficie en las tierras bajas del norte. ^[5] Mientras que las cuencas Hellas , Argyre e Isidis , tienen un gran relieve elevado de Moho y exhiben anillos de corteza engrosada difusa más allá del borde de la corteza. ^[5]

Pero por el contrario, casi todas las cuencas marcianas con un diámetro de 275 km < D < 1000 km están asociadas con una superficie de baja amplitud y un relieve Moho de baja amplitud. ^[25] Incluso se ha descubierto que muchas tienen una anomalía de gravedad en aire libre negativa , aunque la evidencia ha demostrado que todas ellas deberían haber experimentado una gravedad alta (anomalía de gravedad en aire libre positiva). ^[25] Se ha sugerido que estas no fueron causadas solo por la erosión y el enterramiento, ya que la adición de material a la cuenca de hecho aumentaría la fuerza de la gravedad en lugar de disminuirla. ^[25] Por lo tanto, debería haber tenido lugar una relajación viscosa. ^[25] El alto flujo de calor y el alto contenido de agua en la corteza marciana primitiva favorecieron la relajación viscosa. ^[25] Estos dos factores han hecho que la corteza sea más dúctil. La topografía de la cuenca de los cráteres estaría sujeta a una mayor tensión debido a la autogravitación. Tal tensión impulsaría el flujo cortical y, por lo tanto, la descomposición del relieve. Las cuencas de impacto gigantes son las excepciones que no han experimentado relajación viscosa, ya que el adelgazamiento de la corteza ha hecho que esta sea demasiado delgada para sostener el flujo cortical sub-solidus. ^{[5] [25]}

Baja densidad de corteza a granel

El modelo de densidad de la corteza más reciente, RM1, desarrollado en 2017, indica que la densidad de la corteza en masa es de 2582 ± 209 kg m ⁻³ para Marte, ^[9] lo que representa un valor promedio global. ^[9] Debería existir una variación lateral de la densidad de la corteza. ^[9] Por ejemplo, sobre los complejos volcánicos, se espera que la densidad local sea tan alta como 3231 ± 95 kg m ⁻³ , ^[9] lo que coincide con los datos de meteoritos y estimaciones anteriores. Además, la densidad del hemisferio norte es en general más alta que la del hemisferio sur, ^[9] lo que puede implicar que este último es más poroso que el primero.

Para lograr el valor de volumen, la porosidad podría desempeñar un papel importante. Si se elige una densidad de grano mineral de 3100 kg m ⁻³ , ^[9] una porosidad del 10% al 23% podría dar una caída de 200 kg m ⁻³ en la densidad aparente. ^[9] Si los espacios porosos están llenos de agua o hielo, también se espera una disminución de la densidad aparente. ^[9] Una caída adicional en la densidad aparente podría explicarse por el aumento de la densidad con la profundidad, ^[9] con la capa superficial más porosa que la más profunda de Marte, y el aumento de la densidad con la profundidad también tiene variación geográfica. ^[9]

Aplicaciones científicas y de ingeniería

Areoide

La areoide es un geoide planetario que representa la figura equipotencial gravitacional y rotacional de Marte, análoga al concepto de geoide (" nivel del mar ") en la Tierra. ^{[5] [36] [37]} Esto se ha establecido como el marco de referencia para desarrollar los Registros de Datos en Cuadrícula del Experimento de la Misión MOLA (MEGDRs), ^{[5] [36]} que es un modelo topográfico global. El modelo topográfico es importante para mapear las características geomorfológicas y comprender diferentes tipos de procesos en Marte.

Para derivar la areoide, se requieren dos partes de trabajo. Primero, como los datos de gravedad son esenciales para identificar la posición del centro de masa del planeta, ^[36] que se ve afectado en gran medida por la distribución de la masa del interior, son necesarios los datos de seguimiento por radio de las naves espaciales. ^[36] Esto fue realizado en gran medida por el Mars Global Surveyor (MGS). ^{[5] [36]} Luego, el instrumento MOLA 2 a bordo del MGS, que opera en una órbita de elevación de 400 km, podría medir el rango (distancia) entre la nave espacial y la superficie terrestre mediante el conteo del tiempo de ida y vuelta del vuelo del pulso del instrumento. ^[36] La combinación de estos dos trabajos permite construir la areoide y los MEGDR. Con base en lo anterior, la areoide ha tomado el radio como el radio medio del planeta en el ecuador como 3396 km. ^{[5] [36]}

El modelo topográfico MEDGRs se desarrolló a partir de mediciones de rango (distancia) realizadas con el instrumento MOLA 2 y datos de seguimiento por radio del Mars Global Surveyor (MGS). ^[36] El punto más alto se encuentra en el Monte Olimpo, mientras que el punto más profundo se encuentra dentro de la Cuenca Hellas. ^[36] (Marrón-Rojo: Topografía alta; Verde-Azul: Topografía baja) (Crédito: NASA/JPL-Caltech)

Aterrizaje en superficie

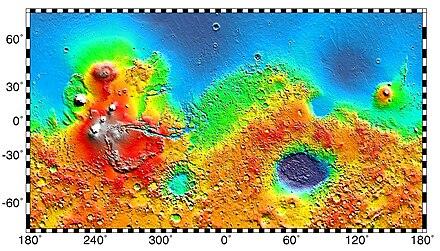
Hay una gran distancia entre Marte y la Tierra, por lo que es casi imposible dar órdenes inmediatas a un módulo de aterrizaje. El aterrizaje depende en gran medida de su sistema autónomo. Para evitar fallos, es esencial comprender con precisión el campo gravitatorio de Marte en los proyectos de aterrizaje, de modo que se puedan minimizar los factores de compensación y las incertidumbres de los efectos gravitacionales, lo que permitiría un aterrizaje sin problemas. ^{[38] [39]} El primer objeto creado por el hombre que aterrizó en Marte, el módulo de aterrizaje Mars 2 , se estrelló por una razón desconocida. Dado que el entorno de la superficie de Marte es complejo y está compuesto de patrones morfológicos que varían lateralmente, para evitar el peligro de rocas, el proceso de aterrizaje debería ser asistido aún más mediante el empleo de LIDAR en el lugar para determinar la posición exacta de aterrizaje y otras medidas de protección. ^{[38] [39]}

Véase también

• Geología de Marte
• La catástrofe de los carbonatos en Marte

Referencias

1. Hirt, C.; Claessens, SJ; Kuhn, M.; Featherstone, WE (2012). "Campo de gravedad de Marte con resolución kilométrica: MGM2011". Ciencia planetaria y espacial . 67 (1): 147–154. Bibcode :2012P&SS...67..147H. doi :10.1016/j.pss.2012.02.006. hdl : 20.500.11937/32270 .
2. Watts, AB; Bodine, JH; Ribe, NM (7 de febrero de 1980). "Observaciones de flexión y evolución geológica de la cuenca del océano Pacífico". Nature . 283 (5747): 532–537. Bibcode :1980Natur.283..532W. doi :10.1038/283532a0. ISSN  1476-4687. S2CID  4333255.
3. Jeffreys, H. (1959). La Tierra 4ª ed., 420.
4. Runcorn, SK (1965). "Cambios en el patrón de convección en el manto terrestre y deriva continental: evidencia de un origen frío de la Tierra". Philosophical Transactions of the Royal Society of London. Serie A, Ciencias matemáticas y físicas . 258 (1088): 228–251. Bibcode :1965RSPTA.258..228R. doi :10.1098/rsta.1965.0037. JSTOR  73348. S2CID  122307704.
5. Neumann, GA; Zuber, MT; Wieczorek, MA; McGovern, PJ; Lemoine, FG; Smith, DE (1 de agosto de 2004). "Estructura de la corteza de Marte a partir de la gravedad y la topografía" (PDF) . Journal of Geophysical Research: Planets . 109 (E8): E08002. Bibcode :2004JGRE..109.8002N. doi : 10.1029/2004je002262 . ISSN  2156-2202.
6. Kiefer, Walter S. (30 de mayo de 2004). "Evidencia gravitacional de una cámara de magma extinta debajo de Syrtis Major, Marte: una mirada al sistema de tuberías magmáticas". Earth and Planetary Science Letters . 222 (2): 349–361. Bibcode :2004E&PSL.222..349K. doi : 10.1016/j.epsl.2004.03.009 .
7. Marty, JC; Balmino, G.; Duron, J.; Rosenblatt, P.; Maistre, S. Le; Rivoldini, A.; Dehant, V.; Hoolst, T. Van (2009). "Modelo del campo gravitatorio marciano y sus variaciones temporales a partir de datos de MGS y Odyssey". Ciencia planetaria y espacial . 57 (3): 350–363. Bibcode :2009P&SS...57..350M. doi :10.1016/j.pss.2009.01.004.
8. Smith, David E.; Zuber, Maria T.; Torrence, Mark H.; Dunn, Peter J.; Neumann, Gregory A.; Lemoine, Frank G.; Fricke, Susan K. (1 de mayo de 2009). "Variaciones temporales del campo gravitacional de Marte y cambios estacionales en las masas de los casquetes polares". Journal of Geophysical Research: Planets . 114 (E5): E05002. Bibcode :2009JGRE..114.5002S. doi :10.1029/2008je003267. hdl : 1721.1/74244 . ISSN  2156-2202.
9. Goossens, Sander; Sabaka, Terence J.; Genova, Antonio; Mazarico, Erwan; Nicholas, Joseph B.; Neumann, Gregory A. (16 de agosto de 2017). "Evidencia de una baja densidad de la corteza en masa para Marte a partir de la gravedad y la topografía". Geophysical Research Letters . 44 (15): 7686–7694. Bibcode :2017GeoRL..44.7686G. doi :10.1002/2017gl074172. ISSN  1944-8007. PMC 5619241 . PMID  28966411. 
10. "Valor CODATA: constante de gravitación newtoniana". Referencia del NIST sobre constantes, unidades e incertidumbre . Instituto Nacional de Estándares y Tecnología de EE. UU . Junio ​​de 2015. Consultado el 14 de diciembre de 2017. "Valores recomendados de CODATA para 2014"
11. Jacobson, RA (2008). Efemérides de los satélites marcianos—MAR080. JPL OIM 343R–08–006 .
12. Kaula, WM (15 de noviembre de 1966). "Pruebas y combinación de determinaciones satelitales del campo gravitatorio con gravimetría". Revista de investigación geofísica . 71 (22): 5303–5314. Bibcode :1966JGR....71.5303K. doi :10.1029/JZ071i022p05303. ISSN  2156-2202.
13. Genova, Antonio; Goossens, Sander; Lemoine, Frank G.; Mazarico, Erwan; Neumann, Gregory A.; Smith, David E.; Zuber, Maria T. (2016). "Campo de gravedad estático y estacional de Marte a partir de la radiociencia MGS, Mars Odyssey y MRO". Icarus . 272 ​​: 228–245. Código Bibliográfico :2016Icar..272..228G. doi :10.1016/j.icarus.2016.02.050.
14. Lemoine, FG; Smith, DE; Rowlands, DD; Zuber, MT; Neumann, GA; Chinn, DS; Pavlis, DE (25 de octubre de 2001). "Una solución mejorada del campo gravitatorio de Marte (GMM-2B) a partir del Mars Global Surveyor". Revista de investigación geofísica: planetas . 106 (E10): 23359–23376. Código Bibliográfico :2001JGR...10623359L. doi : 10.1029/2000je001426 . ISSN  2156-2202.
15. Sinclair, AT (1971-12-01). "Los movimientos de los satélites de Marte". Monthly Notices of the Royal Astronomical Society . 155 (2): 249–274. Bibcode :1971MNRAS.155..249S. doi : 10.1093/mnras/155.2.249 . ISSN  0035-8711.
16. Asmar, SW; Armstrong, JW; Iess, L.; Tortora, P. (1 de abril de 2005). "Seguimiento Doppler de naves espaciales: balance de ruido y precisión alcanzables en observaciones científicas de radio de precisión". Radio Science . 40 (2): RS2001. Bibcode :2005RaSc...40.2001A. doi : 10.1029/2004RS003101 . ISSN  1944-799X.
17. Mayor, Michel; Queloz, Didier (23 de noviembre de 1995). "Una compañera de una estrella de tipo solar con la masa de Júpiter". Nature . 378 (6555): 355–359. Bibcode :1995Natur.378..355M. doi :10.1038/378355a0. ISSN  1476-4687. S2CID  4339201.
18. Gapcynski, JP; Tolson, RH; Michael, WH (30 de septiembre de 1977). "Campo de gravedad de Marte: resultados combinados de Viking y Mariner 9". Revista de investigación geofísica . 82 (28): 4325–4327. Código Bibliográfico :1977JGR....82.4325G. doi :10.1029/js082i028p04325. ISSN  2156-2202.
19. Balmino, G.; Moynot, B.; Valès, N. (1 de enero de 1982). "Modelo del campo gravitatorio de Marte en armónicos esféricos hasta grado y orden dieciocho". Journal of Geophysical Research: Solid Earth . 87 (B12): 9735–9746. Bibcode :1982JGR....87.9735B. doi :10.1029/jb087ib12p09735. ISSN  2156-2202.
20. Smith, DE; Lerch, FJ; Nerem, RS; Zuber, MT; Patel, GB; Fricke, SK; Lemoine, FG (1993-11-25). "Un modelo de gravedad mejorado para Marte: modelo Goddard Mars 1". Revista de investigación geofísica: planetas . 98 (E11): 20871–20889. Bibcode :1993JGR....9820871S. doi :10.1029/93JE01839. ISSN  2156-2202.
21. Konopliv, Alexander S; Sjogren, William L (1 de febrero de 1995). "El campo gravitatorio de Marte del JPL, Mars50c, basado en datos de seguimiento Doppler de Viking y Mariner 9". NASA Sti/Recon Technical Report N . 95 : 30344. Bibcode :1995STIN...9530344K – vía NASA Technical Report Server.
22. Lemoine, FG, 2009. Geociencias NASA PDS. ^{[ enlace roto ]}
23. Konopliv, Alex S.; Yoder, Charles F.; Standish, E. Myles; Yuan, Dah-Ning; Sjogren, William L. (2006). "Una solución global para la gravedad estática y estacional de Marte, la orientación de Marte, las masas de Fobos y Deimos y las efemérides de Marte". Icarus . 182 (1): 23–50. Bibcode :2006Icar..182...23K. doi :10.1016/j.icarus.2005.12.025.
24. Konopliv, Alex S.; Asmar, Sami W.; Folkner, William M.; Karatekin, Özgür; Nunes, Daniel C.; Smrekar, Suzanne E.; Yoder, Charles F.; Zuber, Maria T. (2011). "Campos de gravedad de alta resolución de Marte a partir de MRO, gravedad estacional de Marte y otros parámetros dinámicos". Icarus . 211 (1): 401–428. Bibcode :2011Icar..211..401K. doi :10.1016/j.icarus.2010.10.004.
25. Mohit, P. Surdas; Phillips, Roger J. (1 de noviembre de 2007). "Relajación viscosa en el Marte primitivo: un estudio de cuencas de impacto antiguas". Geophysical Research Letters . 34 (21): L21204. Código Bibliográfico :2007GeoRL..3421204M. doi :10.1029/2007GL031252. ISSN  1944-8007. S2CID  129729097.
26. Airy, GB (1855). "Sobre el cálculo del efecto de la atracción de las masas montañosas, como alteración de la latitud astronómica aparente de las estaciones en los estudios geodésicos". Philosophical Transactions of the Royal Society of London . 145 : 101–104. doi :10.1098/rstl.1855.0003. JSTOR  108511. S2CID  186210268.
27. Beuthe, M.; Le Maistre, S.; Rosenblatt, P.; Pätzold, M.; Dehant, V. (1 de abril de 2012). "Densidad y espesor litosférico de la provincia de Tharsis a partir de datos de gravedad MEX MaRS y MRO". Journal of Geophysical Research: Planets . 117 (E4): E04002. Bibcode :2012JGRE..117.4002B. doi :10.1029/2011je003976. ISSN  2156-2202.
28. Runcorn, SK (1963). "Medidas de gravedad satelital y convección en el manto". Nature . 200 (4907): 628–630. Código Bibliográfico :1963Natur.200..628R. doi :10.1038/200628a0. S2CID  4217054.
29. AB Watts; Daly y SF (1981). "Gravedad de longitud de onda larga y anomalías topográficas". Revista anual de ciencias de la Tierra y planetarias . 9 (1): 415–448. Bibcode :1981AREPS...9..415W. doi :10.1146/annurev.ea.09.050181.002215.
30. McKenzie, Dan (1 de febrero de 1977). "Deformación superficial, anomalías gravitacionales y convección". Revista geofísica de la Royal Astronomical Society . 48 (2): 211–238. Código Bibliográfico :1977GeoJ...48..211M. doi : 10.1111/j.1365-246X.1977.tb01297.x . ISSN  1365-246X.
31. Yoder, CF; Konopliv, AS; Yuan, DN; Standish, EM; Folkner, WM (11 de abril de 2003). "Tamaño del núcleo de fluido de Marte a partir de la detección de la marea solar". Science . 300 (5617): 299–303. Bibcode :2003Sci...300..299Y. CiteSeerX 10.1.1.473.6377 . doi :10.1126/science.1079645. ISSN  0036-8075. PMID  12624177. S2CID  23637169. 
32. Karatekin, Ö.; Van Hoolst, T.; Dehant, V. (1 de junio de 2006). "Intercambio de CO2 a escala global marciano a partir de mediciones de gravedad variables en el tiempo". Journal of Geophysical Research: Planets . 111 (E6): E06003. Bibcode :2006JGRE..111.6003K. doi : 10.1029/2005je002591 . ISSN  2156-2202.
33. Sohl, Frank; Spohn, Tilman (25 de enero de 1997). "La estructura interior de Marte: implicaciones de los meteoritos SNC". Revista de investigación geofísica: planetas . 102 (E1): 1613–1635. Bibcode :1997JGR...102.1613S. CiteSeerX 10.1.1.456.2309 . doi :10.1029/96JE03419. ISSN  2156-2202. 
34. Nimmo, F.; Stevenson, DJ (25 de marzo de 2001). "Estimaciones del espesor de la corteza marciana a partir de la relajación viscosa de la topografía" (PDF) . Journal of Geophysical Research: Planets . 106 (E3): 5085–5098. Bibcode :2001JGR...106.5085N. doi :10.1029/2000JE001331. ISSN  2156-2202.
35. Wieczorek, Mark A.; Zuber, Maria T. (1 de enero de 2004). "Espesor de la corteza marciana: restricciones mejoradas a partir de las relaciones geoide-topografía". Journal of Geophysical Research: Planets . 109 (E1): E01009. Bibcode :2004JGRE..109.1009W. doi : 10.1029/2003JE002153 . ISSN  2156-2202.
36. Smith, David E.; Zuber, Maria T.; Frey, Herbert V.; Garvin, James B.; Head, James W.; Muhleman, Duane O.; Pettengill, Gordon H.; Phillips, Roger J.; Solomon, Sean C. (25 de octubre de 2001). "Altímetro láser Mars Orbiter: resumen del experimento después del primer año de mapeo global de Marte" (PDF) . Journal of Geophysical Research: Planets . 106 (E10): 23689–23722. Bibcode :2001JGR...10623689S. doi :10.1029/2000je001364. ISSN  2156-2202.
37. Ardalan, AA; Karimi, R.; Grafarend, EW (2009). "Una nueva superficie equipotencial de referencia y un elipsoide de referencia para el planeta Marte". Tierra, Luna y planetas . 106 (1): 1–13. doi :10.1007/s11038-009-9342-7. ISSN  0167-9295. S2CID  119952798.
38. Balaram, J., Austin, R., Banerjee, P., Bentley, T., Henriquez, D., Martin, B., ... y Sohl, G. (2002). Dsends: un simulador de dinámica y naves espaciales de alta fidelidad para entrada, descenso y aterrizaje en superficie. En Actas de la Conferencia Aeroespacial, 2002. IEEE (Vol. 7, págs. 7–7). IEEE.
39. Braun, RD; Manning, RM (2007). "Desafíos de la entrada, descenso y aterrizaje en la exploración de Marte". Revista de naves espaciales y cohetes . 44 (2): 310–323. Código Bibliográfico :2007JSpRo..44..310B. CiteSeerX 10.1.1.463.8773 . doi :10.2514/1.25116.