En matemáticas , el teorema de Mohr-Mascheroni establece que cualquier construcción geométrica que pueda realizarse con un compás y una regla puede realizarse solo con un compás.
Debe entenderse que "cualquier construcción geométrica" se refiere a figuras que no contienen líneas rectas, ya que es claramente imposible dibujar una línea recta sin una regla. Se entiende que una línea está determinada siempre que se den o construyan dos puntos distintos en esa línea, aunque no haya una representación visual de la línea. El teorema puede enunciarse de forma más precisa como: [1]
Aunque el uso de una regla puede hacer que la construcción sea significativamente más fácil, el teorema muestra que cualquier conjunto de puntos que defina completamente una figura construida se puede determinar solo con un compás, y la única razón para usar una regla es la estética de ver líneas rectas, lo que para los propósitos de la construcción es funcionalmente innecesario.
El resultado fue publicado originalmente por Georg Mohr en 1672, [2] pero su prueba languideció en la oscuridad hasta 1928. [3] [4] [5] El teorema fue descubierto independientemente por Lorenzo Mascheroni en 1797 y fue conocido como el Teorema de Mascheroni hasta que se redescubrió el trabajo de Mohr. [6]
Se conocen varias demostraciones del resultado. La demostración de Mascheroni de 1797 se basó en general en la idea de utilizar la reflexión en una línea como herramienta principal. La solución de Mohr era diferente. [3] En 1890, August Adler publicó una demostración utilizando la transformación de inversión . [7]
Un enfoque algebraico utiliza el isomorfismo entre el plano euclidiano y el espacio de coordenadas reales . De esta manera, una versión más fuerte del teorema fue demostrada en 1990. [8] También muestra la dependencia del teorema con el axioma de Arquímedes (que no puede formularse en un lenguaje de primer orden ).
Para demostrar el teorema, es necesario demostrar que cada una de las construcciones básicas de compás y regla se pueden realizar utilizando únicamente un compás, ya que son los fundamentos o pasos elementales de todas las demás construcciones. Son:
#1 - Una línea que pasa por dos puntos
Se entiende que no se puede trazar una línea recta sin una regla. Se considera que una línea está dada por dos puntos cualesquiera, ya que cualquier par de ellos define una línea única. De acuerdo con la intención del teorema que pretendemos demostrar, no es necesario trazar la línea real, salvo por razones estéticas.
#2 - Un círculo que pasa por un punto con centro definido
Esto se puede hacer solo con un compás. No se necesita una regla para ello.
#5 - Intersección de dos círculos
Esta construcción también se puede realizar directamente con un compás.
#3, #4 - Las otras construcciones
Por lo tanto, para demostrar el teorema, solo es necesario proporcionar construcciones que utilicen solo brújula para los números 3 y 4.
En este artículo se utilizará la siguiente notación: un círculo cuyo centro se encuentra en el punto U y que pasa por el punto V se denotará por U ( V ) . Un círculo con centro U y radio especificado por un número, r , o un segmento de línea AB se denotará por U ( r ) o U ( AB ) , respectivamente. [9]
En las construcciones generales, a menudo hay varias variantes que producirán el mismo resultado. Las opciones que se elijan en una variante de este tipo se pueden elegir sin perder generalidad. Sin embargo, cuando se utiliza una construcción para demostrar que se puede hacer algo, no es necesario describir todas estas opciones y, en aras de la claridad de la exposición, a continuación solo se dará una variante. Sin embargo, muchas construcciones se presentan en diferentes formas según utilicen o no la inversión del círculo y, si es posible, se darán estas alternativas.
También es importante señalar que algunas de las construcciones que se presentan a continuación para demostrar el teorema de Mohr-Mascheroni requieren la colocación arbitraria de puntos en el espacio, como por ejemplo, encontrar el centro de un círculo cuando no se ha proporcionado previamente (véase la construcción a continuación). En algunos paradigmas de construcción (como en la definición geométrica del número construible ), la colocación arbitraria de puntos puede estar prohibida. Sin embargo, en un paradigma de este tipo, por ejemplo, existen varias construcciones de modo que la colocación arbitraria de puntos es innecesaria. También vale la pena señalar que no se podría construir ningún círculo sin el compás, por lo que en la práctica no hay ninguna razón para que no exista un punto central.
Para demostrar las construcciones n.° 3 y n.° 4 anteriores, que se incluyen a continuación, también se explican algunas construcciones intermedias necesarias, ya que se utilizan y se hace referencia a ellas con frecuencia. Estas también son construcciones que solo se basan en la brújula. Todas las construcciones que se indican a continuación se basan en las construcciones n.° 1, n.° 2, n.° 5 y cualquier otra construcción que se indique antes.
La capacidad de trasladar o copiar un círculo a un nuevo centro es vital en estas demostraciones y fundamental para establecer la veracidad del teorema. La creación de un nuevo círculo con el mismo radio que el primero, pero centrado en un punto diferente, es la característica clave que distingue al compás colapsable del compás rígido moderno. Con el compás rígido esto es una trivialidad, pero con el compás colapsable es una cuestión de posibilidad de construcción. La equivalencia de un compás colapsable y un compás rígido fue demostrada por Euclides (Libro I Proposición 2 de Los Elementos ) utilizando una regla y un compás colapsable cuando, esencialmente, construye una copia de un círculo con un centro diferente. Esta equivalencia también puede establecerse solo con el compás (colapsable), una demostración de la cual se puede encontrar en el artículo principal.

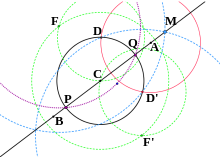
Esta construcción se puede repetir tantas veces como sea necesario para encontrar un punto Q tal que la longitud del segmento de línea AQ = n ⋅ longitud del segmento de línea AB para cualquier entero positivo n .

El punto I es tal que el radio r de B ( r ) es a IB como DB es al radio; o IB / r = r / DB .
En el caso de que la construcción anterior falle (es decir, el círculo rojo y el círculo negro no se intersequen en dos puntos), [10] encuentre un punto Q en la línea BD tal que la longitud del segmento de línea BQ sea un múltiplo entero positivo, digamos n , de la longitud de BD y sea mayor que r / 2 (esto es posible por el axioma de Arquímedes). Encuentre Q' la inversa de Q en el círculo B ( r ) como arriba (los círculos rojo y negro ahora deben intersecar en dos puntos). El punto I ahora se obtiene extendiendo BQ' tal que BI = n ⋅ BQ' .


La construcción, utilizando solo el compás, de los puntos de intersección de una línea y un círculo se divide en dos casos dependiendo de si el centro del círculo es o no colineal con la línea.
Supongamos que el centro del círculo no está en la línea.

También se puede dar una construcción alternativa, utilizando la inversión del círculo. [12]
De esta manera se ha demostrado que todas las construcciones básicas que se pueden realizar con una regla y un compás se pueden realizar solo con un compás, siempre que se entienda que una línea no se puede dibujar literalmente sino simplemente definir mediante dos puntos.
Los matemáticos renacentistas Lodovico Ferrari , Gerolamo Cardano y Niccolò Fontana Tartaglia y otros pudieron demostrar en el siglo XVI que cualquier construcción con regla y compás podía lograrse con una regla y un compás de ancho fijo (es decir, un compás oxidado). [16]
El teorema de equivalencia de la brújula muestra que en todas las construcciones mencionadas anteriormente, la brújula moderna, con su apertura fijable, que se puede utilizar para transferir distancias, se puede reemplazar por una "brújula plegable", una brújula que se pliega cuando se la levanta de una página, de modo que no se puede utilizar directamente para transferir distancias. De hecho, las construcciones originales de Euclides utilizan una brújula plegable. Es posible trasladar cualquier círculo en el plano con una brújula plegable utilizando no más de tres aplicaciones adicionales de la brújula además de las de una brújula rígida.
Motivado por el resultado de Mascheroni, en 1822 Jean Victor Poncelet conjeturó una variación sobre el mismo tema. Su trabajo allanó el camino para el campo de la geometría proyectiva , en el que propuso que cualquier construcción posible con regla y compás podría hacerse solo con regla. Sin embargo, la única condición es que se debe proporcionar no menos de un círculo con su centro identificado. Esta afirmación, ahora conocida como el teorema de Poncelet-Steiner , fue demostrada por Jakob Steiner once años después.
Una prueba proporcionada posteriormente en 1904 por Francesco Severi relaja el requisito de que se proporcione un círculo completo y muestra que cualquier arco pequeño del círculo, siempre que se proporcione el centro, sigue siendo suficiente. [17]
Además, se puede omitir el centro en sí en lugar de partes del arco, si se lo sustituye por algo más suficiente, como un segundo círculo concéntrico, un segundo círculo que se interseca o un tercer círculo en el plano. Alternativamente, un segundo círculo que no se interseca ni es concéntrico es suficiente, siempre que se dé un punto en la línea central que los atraviesa o en el eje radical entre ellos, o que existan dos líneas paralelas en el plano. Un solo círculo sin su centro también puede ser suficiente en las circunstancias adecuadas. Pueden existir otras condiciones únicas.