Método de elementos finitos

Método numérico para resolver problemas físicos o de ingeniería.

Visualización de cómo se deforma un automóvil en un choque asimétrico mediante análisis de elementos finitos

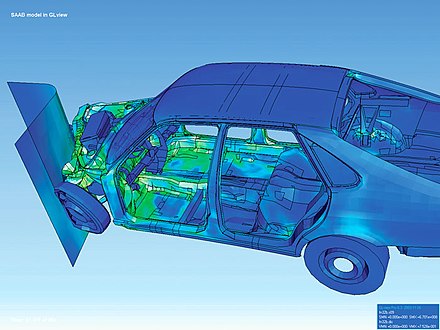
El método de elementos finitos ( MEF ) es un método popular para resolver numéricamente ecuaciones diferenciales que surgen en ingeniería y modelado matemático . Las áreas problemáticas de interés típicas incluyen los campos tradicionales de análisis estructural , transferencia de calor , flujo de fluidos , transporte de masa y potencial electromagnético . Por lo general, se utilizan computadoras para realizar los cálculos necesarios. Con supercomputadoras de alta velocidad , se pueden lograr mejores soluciones y, a menudo, se requieren para resolver los problemas más grandes y complejos.

El método de elementos finitos (FEM) es un método numérico general para resolver ecuaciones diferenciales parciales en dos o tres variables espaciales (es decir, algunos problemas de valores en la frontera ). También hay estudios sobre el uso del FEM para resolver problemas de alta dimensión. ^[1] Para resolver un problema, el FEM subdivide un sistema grande en partes más pequeñas y simples llamadas elementos finitos . Esto se logra mediante una discretización espacial particular en las dimensiones espaciales, que se implementa mediante la construcción de una malla del objeto: el dominio numérico para la solución, que tiene un número finito de puntos. La formulación del método de elementos finitos de un problema de valores en la frontera finalmente da como resultado un sistema de ecuaciones algebraicas . El método aproxima la función desconocida sobre el dominio. ^[2] Las ecuaciones simples que modelan estos elementos finitos se ensamblan luego en un sistema más grande de ecuaciones que modela todo el problema. Luego, el FEM aproxima una solución al minimizar una función de error asociada a través del cálculo de variaciones .

El estudio o análisis de un fenómeno con FEM a menudo se denomina análisis de elementos finitos ( FEA ).

Conceptos básicos

La subdivisión de un dominio completo en partes más simples tiene varias ventajas: ^[3]

• Representación precisa de geometría compleja
• Inclusión de propiedades de materiales diferentes
• Representación sencilla de la solución total
• Captura de efectos locales.

El funcionamiento típico del método implica:

1. dividir el dominio del problema en una colección de subdominios, con cada subdominio representado por un conjunto de ecuaciones de elementos del problema original
2. recombinando sistemáticamente todos los conjuntos de ecuaciones de elementos en un sistema global de ecuaciones para el cálculo final.

El sistema global de ecuaciones tiene técnicas de solución conocidas y puede calcularse a partir de los valores iniciales del problema original para obtener una respuesta numérica.

En el primer paso anterior, las ecuaciones de los elementos son ecuaciones simples que aproximan localmente las ecuaciones complejas originales que se van a estudiar, donde las ecuaciones originales suelen ser ecuaciones diferenciales parciales (EDP). Para explicar la aproximación en este proceso, el método de elementos finitos se introduce comúnmente como un caso especial del método de Galerkin . El proceso, en lenguaje matemático, consiste en construir una integral del producto interno del residuo y las funciones de peso y establecer la integral en cero. En términos simples, es un procedimiento que minimiza el error de aproximación al ajustar funciones de prueba en la EDP. El residuo es el error causado por las funciones de prueba, y las funciones de peso son funciones de aproximación polinómica que proyectan el residuo. El proceso elimina todas las derivadas espaciales de la EDP, aproximando así la EDP localmente con

• un conjunto de ecuaciones algebraicas para problemas de estado estacionario ,
• un conjunto de ecuaciones diferenciales ordinarias para problemas transitorios .

Estos conjuntos de ecuaciones son ecuaciones elementales. Son lineales si la ecuación diferencial parcial subyacente es lineal y viceversa. Los conjuntos de ecuaciones algebraicas que surgen en los problemas de estado estable se resuelven utilizando métodos numéricos de álgebra lineal . Por el contrario, los conjuntos de ecuaciones diferenciales ordinarias que surgen en los problemas transitorios se resuelven mediante integración numérica utilizando técnicas estándar como el método de Euler o el método de Runge-Kutta .

En el paso (2) anterior, se genera un sistema global de ecuaciones a partir de las ecuaciones de los elementos transformando las coordenadas de los nodos locales de los subdominios en nodos globales del dominio. Esta transformación espacial incluye ajustes de orientación apropiados aplicados en relación con el sistema de coordenadas de referencia . El proceso se lleva a cabo a menudo mediante software FEM utilizando datos de coordenadas generados a partir de los subdominios.

La aplicación práctica del método de elementos finitos se conoce como análisis de elementos finitos (FEA). El FEA, tal como se aplica en ingeniería , es una herramienta computacional para realizar análisis de ingeniería . Incluye el uso de técnicas de generación de mallas para dividir un problema complejo en elementos pequeños, así como el uso de software codificado con un algoritmo FEM. Al aplicar el FEA, el problema complejo suele ser un sistema físico con la física subyacente , como la ecuación de la viga de Euler-Bernoulli , la ecuación del calor o las ecuaciones de Navier-Stokes expresadas en ecuaciones diferenciales parciales o ecuaciones integrales , mientras que los elementos pequeños divididos del problema complejo representan diferentes áreas en el sistema físico.

El método FEA se puede utilizar para analizar problemas en dominios complicados (como automóviles y oleoductos) cuando el dominio cambia (como durante una reacción de estado sólido con un límite móvil), cuando la precisión deseada varía en todo el dominio o cuando la solución carece de suavidad. Las simulaciones FEA proporcionan un recurso valioso, ya que eliminan múltiples instancias de creación y prueba de prototipos complejos para varias situaciones de alta fidelidad. ^{[ cita requerida ]} Por ejemplo, en una simulación de choque frontal, es posible aumentar la precisión de la predicción en áreas "importantes" como la parte delantera del automóvil y reducirla en su parte trasera (reduciendo así el costo de la simulación). Otro ejemplo sería la predicción numérica del tiempo , donde es más importante tener predicciones precisas sobre fenómenos en desarrollo altamente no lineales (como ciclones tropicales en la atmósfera o remolinos en el océano) en lugar de áreas relativamente tranquilas.

Una presentación clara, detallada y práctica de este enfoque se puede encontrar en el libro de texto El método de elementos finitos para ingenieros . ^[4]

Historia

Si bien es difícil citar la fecha de la invención del método de elementos finitos, el método se originó a partir de la necesidad de resolver problemas complejos de elasticidad y análisis estructural en ingeniería civil y aeronáutica . ^[5] Su desarrollo se remonta al trabajo de Alexander Hrennikoff ^[6] y Richard Courant ^[7] a principios de la década de 1940. Otro pionero fue Ioannis Argyris . En la URSS, la introducción de la aplicación práctica del método generalmente se relaciona con el nombre de Leonard Oganesyan. ^[8] También fue redescubierto independientemente en China por Feng Kang a fines de la década de 1950 y principios de la de 1960, basado en los cálculos de construcciones de presas, donde se denominó método de diferencias finitas basado en el principio de variación . Aunque los enfoques utilizados por estos pioneros son diferentes, comparten una característica esencial: la discretización de malla de un dominio continuo en un conjunto de subdominios discretos, generalmente llamados elementos.

El trabajo de Hrennikoff discretiza el dominio utilizando una analogía de red , mientras que el enfoque de Courant divide el dominio en subregiones triangulares finitas para resolver ecuaciones diferenciales parciales elípticas de segundo orden que surgen del problema de la torsión de un cilindro . La contribución de Courant fue evolutiva, basándose en un gran cuerpo de resultados anteriores para ecuaciones en derivadas parciales desarrollados por Lord Rayleigh , Walther Ritz y Boris Galerkin .

El método de elementos finitos obtuvo su verdadero impulso en los años 1960 y 1970 con los desarrollos de JH Argyris con colaboradores de la Universidad de Stuttgart , RW Clough con colaboradores de la UC Berkeley , OC Zienkiewicz con colaboradores Ernest Hinton , Bruce Irons ^[9] y otros en la Universidad de Swansea , Philippe G. Ciarlet en la Universidad de París 6 y Richard Gallagher con colaboradores de la Universidad de Cornell . Un mayor impulso fue proporcionado en estos años por los programas de elementos finitos de código abierto disponibles. La NASA patrocinó la versión original de NASTRAN . UC Berkeley hizo que los programas de elementos finitos SAP IV ^[10] y más tarde OpenSees estuvieran ampliamente disponibles. En Noruega, la sociedad de clasificación de barcos Det Norske Veritas (ahora DNV GL ) desarrolló Sesam en 1969 para su uso en el análisis de barcos. ^{[11] En 1973,} Gilbert Strang y George Fix proporcionaron una base matemática rigurosa para el método de elementos finitos . ^[12] Desde entonces, el método se ha generalizado para el modelado numérico de sistemas físicos en una amplia variedad de disciplinas de ingeniería , por ejemplo, electromagnetismo , transferencia de calor y dinámica de fluidos . ^{[13] [14]}

Discusión técnica

La estructura de los métodos de elementos finitos

Un método de elementos finitos se caracteriza por una formulación variacional , una estrategia de discretización, uno o más algoritmos de solución y procedimientos de posprocesamiento.

Ejemplos de la formulación variacional son el método de Galerkin , el método de Galerkin discontinuo, los métodos mixtos, etc.

Por estrategia de discretización se entiende un conjunto claramente definido de procedimientos que cubren (a) la creación de mallas de elementos finitos, (b) la definición de la función base sobre elementos de referencia (también llamadas funciones de forma), y (c) el mapeo de elementos de referencia sobre los elementos de la malla. Ejemplos de estrategias de discretización son la versión h, la versión p , la versión hp , x-FEM , el análisis isogeométrico , etc. Cada estrategia de discretización tiene ciertas ventajas y desventajas. Un criterio razonable para seleccionar una estrategia de discretización es lograr un rendimiento casi óptimo para el conjunto más amplio de modelos matemáticos en una clase de modelo particular.

Los distintos algoritmos de solución numérica se pueden clasificar en dos grandes categorías: solucionadores directos e iterativos. Estos algoritmos están diseñados para aprovechar la escasez de matrices que dependen de la formulación variacional y de las opciones de estrategia de discretización.

Los procedimientos de posprocesamiento están diseñados para extraer los datos de interés de una solución de elementos finitos. Para cumplir con los requisitos de verificación de la solución, los posprocesadores deben prever una estimación de errores a posteriori en términos de las cantidades de interés. Cuando los errores de aproximación son mayores que lo que se considera aceptable, entonces la discretización debe modificarse ya sea mediante un proceso adaptativo automatizado o por la acción del analista. Algunos posprocesadores muy eficientes permiten la realización de la superconvergencia .

Problemas ilustrativos P1 y P2

Los dos problemas siguientes demuestran el método de elementos finitos.

P1 es un problema unidimensional donde se da, es una función desconocida de y es la segunda derivada de con respecto a . $${\displaystyle {\text{ P1 }}:{\begin{cases}u''(x)=f(x){\text{ in }}(0,1),\\u(0)=u(1)=0,\end{cases}}}$$ ${\displaystyle f}$ ${\displaystyle u}$ ${\displaystyle x}$ ${\displaystyle u''}$ ${\displaystyle u}$ ${\displaystyle x}$

P2 es un problema bidimensional ( problema de Dirichlet ) $${\displaystyle {\text{P2 }}:{\begin{cases}u_{xx}(x,y)+u_{yy}(x,y)=f(x,y)&{\text{ in }}\Omega ,\\u=0&{\text{ on }}\partial \Omega ,\end{cases}}}$$

donde es una región abierta conexa en el plano cuyo límite es agradable (por ejemplo, una variedad suave o un polígono ), y y denotan las segundas derivadas con respecto a y , respectivamente. ${\displaystyle \Omega }$ ${\displaystyle (x,y)}$ ${\displaystyle \partial \Omega }$ ${\displaystyle u_{xx}}$ ${\displaystyle u_{yy}}$ ${\displaystyle x}$ ${\displaystyle y}$

El problema P1 se puede resolver directamente calculando antiderivadas . Sin embargo, este método de resolución del problema de valores en la frontera (BVP) funciona solo cuando hay una dimensión espacial. No se generaliza a problemas de dimensiones superiores o problemas como . Por este motivo, desarrollaremos el método de elementos finitos para P1 y describiremos su generalización a P2. ${\displaystyle u+V''=f}$

Nuestra explicación se desarrollará en dos pasos, que reflejan dos pasos esenciales que uno debe seguir para resolver un problema de valor límite (BVP) utilizando el FEM.

• En el primer paso, se reformula el BVP original en su forma débil. Normalmente, para este paso se requiere poco o ningún cálculo. La transformación se realiza a mano en papel.
• El segundo paso es la discretización, donde la forma débil se discretiza en un espacio de dimensión finita.

Después de este segundo paso, tenemos fórmulas concretas para un problema lineal grande pero de dimensión finita cuya solución resolverá aproximadamente el BVP original. Este problema de dimensión finita se implementa luego en una computadora .

Formulación débil

El primer paso es convertir P1 y P2 en sus formulaciones débiles equivalentes .

La forma débil de P1

Si resuelve P1, entonces para cualquier función suave que satisfaga las condiciones de contorno de desplazamiento, es decir en y , tenemos ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle v=0}$ ${\displaystyle x=0}$ ${\displaystyle x=1}$

Por el contrario, si con satisface (1) para cada función suave , entonces se puede demostrar que esto resolverá P1. La prueba es más fácil para la diferenciabilidad continua dos veces ( teorema del valor medio ), pero también se puede demostrar en un sentido distributivo . ${\displaystyle u}$ ${\displaystyle u(0)=u(1)=0}$ ${\displaystyle v(x)}$ ${\displaystyle u}$ ${\displaystyle u}$

Definimos un nuevo operador o mapa utilizando la integración por partes en el lado derecho de (1): ${\displaystyle \phi (u,v)}$

donde hemos utilizado el supuesto de que . ${\displaystyle v(0)=v(1)=0}$

La forma débil de P2

Si integramos por partes usando una forma de identidades de Green , vemos que si resuelve P2, entonces podemos definir para cualquier por ${\displaystyle u}$ ${\displaystyle \phi (u,v)}$ ${\displaystyle v}$ $${\displaystyle \int _{\Omega }fv\,ds=-\int _{\Omega }\nabla u\cdot \nabla v\,ds\equiv -\phi (u,v),}$$

donde denota el gradiente y denota el producto escalar en el plano bidimensional. Una vez más se puede convertir en un producto interno en un espacio adecuado de funciones una vez diferenciables de que son cero en . También hemos asumido que (ver espacios de Sobolev ). También se puede demostrar la existencia y unicidad de la solución. ${\displaystyle \nabla }$ ${\displaystyle \cdot }$ ${\displaystyle \,\!\phi }$ ${\displaystyle H_{0}^{1}(\Omega )}$ ${\displaystyle \Omega }$ ${\displaystyle \partial \Omega }$ ${\displaystyle v\in H_{0}^{1}(\Omega )}$

Un esquema de prueba de la existencia y unicidad de la solución.

Podemos pensar libremente en que son las funciones absolutamente continuas de que están en y (ver espacios de Sobolev ). Tales funciones son (débilmente) una vez diferenciables, y resulta que la función bilineal simétrica define entonces un producto interno que se convierte en un espacio de Hilbert (una prueba detallada no es trivial). Por otro lado, el lado izquierdo también es un producto interno, esta vez en el espacio Lp . Una aplicación del teorema de representación de Riesz para espacios de Hilbert muestra que hay una solución única (2) y, por lo tanto, P1. Esta solución es a priori solo un miembro de , pero utilizando regularidad elíptica , será suave si es . ${\displaystyle H_{0}^{1}(0,1)}$ ${\displaystyle (0,1)}$ ${\displaystyle 0}$ ${\displaystyle x=0}$ ${\displaystyle x=1}$ ${\displaystyle \!\,\phi }$ ${\displaystyle H_{0}^{1}(0,1)}$ ${\displaystyle \int _{0}^{1}f(x)v(x)dx}$ ${\displaystyle L^{2}(0,1)}$ ${\displaystyle u}$ ${\displaystyle H_{0}^{1}(0,1)}$ ${\displaystyle f}$

Discretización

Una función con valores cero en los puntos finales (azul) y una aproximación lineal por partes (rojo) ${\displaystyle H_{0}^{1},}$

P1 y P2 están listos para ser discretizados, lo que conduce a un subproblema común (3). La idea básica es reemplazar el problema lineal de dimensión infinita:

Encuentra tal que ${\displaystyle u\in H_{0}^{1}}$

${\displaystyle \forall v\in H_{0}^{1},\;-\phi (u,v)=\int fv}$

con una versión de dimensión finita:

donde es un subespacio de dimensión finita de . Hay muchas opciones posibles para (una posibilidad lleva al método espectral ). Sin embargo, tomamos como un espacio de funciones polinómicas por partes para el método de elementos finitos. ${\displaystyle V}$ ${\displaystyle H_{0}^{1}}$ ${\displaystyle V}$ ${\displaystyle V}$

Para el problema P1

Tomamos el intervalo , elegimos valores de con y definimos por: ${\displaystyle (0,1)}$ ${\displaystyle n}$ ${\displaystyle x}$ ${\displaystyle 0=x_{0}<x_{1}<\cdots <x_{n}<x_{n+1}=1}$ ${\displaystyle V}$ $${\displaystyle V=\{v:[0,1]\to \mathbb {R} \;:v{\text{ is continuous, }}v|_{[x_{k},x_{k+1}]}{\text{ is linear for }}k=0,\dots ,n{\text{, and }}v(0)=v(1)=0\}}$$

donde definimos y . Observe que las funciones en no son diferenciables según la definición elemental del cálculo. De hecho, si entonces la derivada normalmente no está definida en ningún , . Sin embargo, la derivada existe en cualquier otro valor de , y se puede usar esta derivada para la integración por partes . ${\displaystyle x_{0}=0}$ ${\displaystyle x_{n+1}=1}$ ${\displaystyle V}$ ${\displaystyle v\in V}$ ${\displaystyle x=x_{k}}$ ${\displaystyle k=1,\ldots ,n}$ ${\displaystyle x}$

Una función lineal por partes en dos dimensiones

Para el problema P2

Necesitamos que sea un conjunto de funciones de . En la figura de la derecha, hemos ilustrado una triangulación de una región poligonal de 15 lados en el plano (abajo), y una función lineal por partes (arriba, en color) de este polígono que es lineal en cada triángulo de la triangulación; el espacio estaría formado por funciones que son lineales en cada triángulo de la triangulación elegida. ${\displaystyle V}$ ${\displaystyle \Omega }$ ${\displaystyle \Omega }$ ${\displaystyle V}$

Se espera que a medida que la malla triangular subyacente se vuelve cada vez más fina, la solución del problema discreto (3) converja, en cierto sentido, a la solución del problema de valor límite original P2. Para medir esta finura de la malla, la triangulación se indexa mediante un parámetro de valor real que se considera muy pequeño. Este parámetro estará relacionado con el tamaño de triángulo más grande o promedio en la triangulación. A medida que refinamos la triangulación, el espacio de funciones lineales por partes también debe cambiar con . Por esta razón, a menudo se lee en lugar de en la literatura. Dado que no realizamos dicho análisis, no utilizaremos esta notación. ${\displaystyle h>0}$ ${\displaystyle V}$ ${\displaystyle h}$ ${\displaystyle V_{h}}$ ${\displaystyle V}$

Elección de una base

Interpolación de una función de Bessel

Para completar la discretización, debemos seleccionar una base de . En el caso unidimensional, para cada punto de control elegiremos la función lineal por partes en cuyo valor sea en y cero en cada , es decir, ${\displaystyle V}$ ${\displaystyle x_{k}}$ ${\displaystyle v_{k}}$ ${\displaystyle V}$ ${\displaystyle 1}$ ${\displaystyle x_{k}}$ ${\displaystyle x_{j},\;j\neq k}$ $${\displaystyle v_{k}(x)={\begin{cases}{x-x_{k-1} \over x_{k}\,-x_{k-1}}&{\text{ if }}x\in [x_{k-1},x_{k}],\\{x_{k+1}\,-x \over x_{k+1}\,-x_{k}}&{\text{ if }}x\in [x_{k},x_{k+1}],\\0&{\text{ otherwise}},\end{cases}}}$$

para ; esta base es una función de tienda desplazada y escalada . Para el caso bidimensional, elegimos nuevamente una función de base por vértice de la triangulación de la región plana . La función es la única función de cuyo valor es en y cero en cada . ${\displaystyle k=1,\dots ,n}$ ${\displaystyle v_{k}}$ ${\displaystyle x_{k}}$ ${\displaystyle \Omega }$ ${\displaystyle v_{k}}$ ${\displaystyle V}$ ${\displaystyle 1}$ ${\displaystyle x_{k}}$ ${\displaystyle x_{j},\;j\neq k}$

Según el autor, la palabra "elemento" en el "método de elementos finitos" se refiere a los triángulos del dominio, a la función base lineal por partes o a ambos. Así, por ejemplo, un autor interesado en dominios curvos podría reemplazar los triángulos con primitivos curvos y, por lo tanto, podría describir los elementos como curvilíneos. Por otro lado, algunos autores reemplazan "lineal por partes" con "cuadrático por partes" o incluso "polinomio por partes". El autor podría entonces decir "elemento de orden superior" en lugar de "polinomio de grado superior". El método de elementos finitos no se limita a triángulos (tetraedros en 3-d o símplex de orden superior en espacios multidimensionales). Sin embargo, se puede definir en subdominios cuadriláteros (hexaedros, prismas o pirámides en 3-d, etc.). Las formas de orden superior (elementos curvilíneos) se pueden definir con formas polinómicas e incluso no polinómicas (por ejemplo, elipse o círculo).

Ejemplos de métodos que utilizan funciones base polinomiales por partes de grado superior son el hp-FEM y el FEM espectral .

Las implementaciones más avanzadas (métodos de elementos finitos adaptativos) utilizan un método para evaluar la calidad de los resultados (basado en la teoría de estimación de errores) y modifican la malla durante la solución con el objetivo de lograr una solución aproximada dentro de ciertos límites a partir de la solución exacta del problema continuo. La adaptabilidad de la malla puede utilizar varias técnicas; las más populares son:

• nodos móviles (r-adaptabilidad)
• Elementos refinados (y no refinados) (h-adaptabilidad)
• cambio de orden de funciones base (p-adaptabilidad)
• combinaciones de los anteriores ( hp-adaptividad ).

Pequeño apoyo de la base

Resolver el problema bidimensional en el disco centrado en el origen y radio 1, con condiciones de borde cero. (a) La triangulación. ${\displaystyle u_{xx}+u_{yy}=-4}$

(b) La matriz dispersa L del sistema lineal discretizado

(c) La solución calculada, ${\displaystyle u(x,y)=1-x^{2}-y^{2}}$

La principal ventaja de esta elección de base es que los productos internos de y serán cero para casi todos los . (La matriz que contiene en la ubicación se conoce como matriz de Gram ). En el caso unidimensional, el soporte de es el intervalo . Por lo tanto, los integrandos de y son idénticamente cero siempre que . $${\displaystyle \langle v_{j},v_{k}\rangle =\int _{0}^{1}v_{j}v_{k}\,dx}$$ $${\displaystyle \phi (v_{j},v_{k})=\int _{0}^{1}v_{j}'v_{k}'\,dx}$$ ${\displaystyle j,k}$ ${\displaystyle \langle v_{j},v_{k}\rangle }$ ${\displaystyle (j,k)}$ ${\displaystyle v_{k}}$ ${\displaystyle [x_{k-1},x_{k+1}]}$ ${\displaystyle \langle v_{j},v_{k}\rangle }$ ${\displaystyle \phi (v_{j},v_{k})}$ ${\displaystyle |j-k|>1}$

De manera similar, en el caso planar, si y no comparten un borde de la triangulación, entonces las integrales y son ambas cero. ${\displaystyle x_{j}}$ ${\displaystyle x_{k}}$ $${\displaystyle \int _{\Omega }v_{j}v_{k}\,ds}$$ $${\displaystyle \int _{\Omega }\nabla v_{j}\cdot \nabla v_{k}\,ds}$$

Forma matricial del problema

Si escribimos y luego el problema (3), tomando para , se convierte en ${\displaystyle u(x)=\sum _{k=1}^{n}u_{k}v_{k}(x)}$ ${\displaystyle f(x)=\sum _{k=1}^{n}f_{k}v_{k}(x)}$ ${\displaystyle v(x)=v_{j}(x)}$ ${\displaystyle j=1,\dots ,n}$

Si denotamos por y los vectores columna y , y si dejamos que y sean matrices cuyas entradas son y entonces podemos reformular (4) como ${\displaystyle \mathbf {u} }$ ${\displaystyle \mathbf {f} }$ ${\displaystyle (u_{1},\dots ,u_{n})^{t}}$ ${\displaystyle (f_{1},\dots ,f_{n})^{t}}$ $${\displaystyle L=(L_{ij})}$$ $${\displaystyle M=(M_{ij})}$$ $${\displaystyle L_{ij}=\phi (v_{i},v_{j})}$$ $${\displaystyle M_{ij}=\int v_{i}v_{j}dx}$$

No es necesario suponer . Para una función general , el problema (3) con para se vuelve en realidad más simple, ya que no se utiliza ninguna matriz , ${\displaystyle f(x)=\sum _{k=1}^{n}f_{k}v_{k}(x)}$ ${\displaystyle f(x)}$ ${\displaystyle v(x)=v_{j}(x)}$ ${\displaystyle j=1,\dots ,n}$ ${\displaystyle M}$

donde y para . ${\displaystyle \mathbf {b} =(b_{1},\dots ,b_{n})^{t}}$ ${\displaystyle b_{j}=\int fv_{j}dx}$ ${\displaystyle j=1,\dots ,n}$

Como hemos comentado antes, la mayoría de las entradas de y son cero porque las funciones base tienen un soporte pequeño. Por lo tanto, ahora tenemos que resolver un sistema lineal en la incógnita donde la mayoría de las entradas de la matriz , que necesitamos invertir, son cero. ${\displaystyle L}$ ${\displaystyle M}$ ${\displaystyle v_{k}}$ ${\displaystyle \mathbf {u} }$ ${\displaystyle L}$

Estas matrices se conocen como matrices dispersas y existen solucionadores eficientes para tales problemas (mucho más eficientes que invertir realmente la matriz). Además, es simétrica y definida positiva, por lo que se favorece una técnica como el método del gradiente conjugado . Para problemas que no son demasiado grandes, las descomposiciones LU dispersas y las descomposiciones de Cholesky aún funcionan bien. Por ejemplo, el operador de barra invertida de MATLAB (que utiliza LU dispersas, Cholesky dispersas y otros métodos de factorización) puede ser suficiente para mallas con cien mil vértices. ${\displaystyle L}$

La matriz generalmente se denomina matriz de rigidez , mientras que la matriz se denomina matriz de masa . ${\displaystyle L}$ ${\displaystyle M}$

Forma general del método de elementos finitos

En general, el método de elementos finitos se caracteriza por el siguiente proceso.

• Se elige una cuadrícula para . En el tratamiento anterior, la cuadrícula estaba formada por triángulos, pero también se pueden utilizar cuadrados o polígonos curvilíneos. ${\displaystyle \Omega }$
• Luego, se eligen las funciones base. En nuestro análisis, utilizamos funciones base lineales por partes, pero es común utilizar funciones base polinómicas por partes.

Una consideración aparte es la suavidad de las funciones base. Para problemas de valores de contorno elípticos de segundo orden , basta con una función base polinómica por partes que sea simplemente continua (es decir, las derivadas sean discontinuas). Para ecuaciones diferenciales parciales de orden superior, se deben utilizar funciones base más suaves. Por ejemplo, para un problema de cuarto orden como , se pueden utilizar funciones base cuadráticas por partes que sean . ${\displaystyle u_{xxxx}+u_{yyyy}=f}$ ${\displaystyle C^{1}}$

Otra consideración es la relación del espacio de dimensión finita con su contraparte de dimensión infinita en los ejemplos anteriores . Un método de elementos conformes es uno en el que el espacio es un subespacio del espacio de elementos para el problema continuo. El ejemplo anterior es un método de este tipo. Si no se cumple esta condición, obtenemos un método de elementos no conformes, un ejemplo del cual es el espacio de funciones lineales por partes sobre la malla, que son continuas en cada punto medio de los bordes. Dado que estas funciones son generalmente discontinuas a lo largo de los bordes, este espacio de dimensión finita no es un subespacio del original . ${\displaystyle V}$ ${\displaystyle H_{0}^{1}}$ ${\displaystyle V}$ ${\displaystyle H_{0}^{1}}$

Por lo general, se tiene un algoritmo para subdividir una malla dada. Si el método principal para aumentar la precisión es subdividir la malla, se tiene un método h ( h es habitualmente el diámetro del elemento más grande de la malla). De esta manera, si se demuestra que el error con una cuadrícula está acotado por encima de , para algunos y , entonces se tiene un método de orden p . Bajo hipótesis específicas (por ejemplo, si el dominio es convexo), un método de polinomio por partes de orden tendrá un error de orden . ${\displaystyle h}$ ${\displaystyle Ch^{p}}$ ${\displaystyle C<\infty }$ ${\displaystyle p>0}$ ${\displaystyle d}$ ${\displaystyle p=d+1}$

Si en lugar de hacer h más pequeño, se aumenta el grado de los polinomios utilizados en la función base, se obtiene un método p . Si se combinan estos dos tipos de refinamiento, se obtiene un método hp ( hp-FEM ). En el hp-FEM, los grados de los polinomios pueden variar de un elemento a otro. Los métodos de orden superior con valores p uniformes grandes se denominan métodos de elementos finitos espectrales ( SFEM ). Estos no deben confundirse con los métodos espectrales .

Para ecuaciones diferenciales parciales vectoriales, las funciones base pueden tomar valores en . ${\displaystyle \mathbb {R} ^{n}}$

Diversos tipos de métodos de elementos finitos

AEM

El método de elementos aplicados o AEM combina características tanto del método FEM como del método de elementos discretos o (DEM).

A-FEM

Yang y Lui introdujeron el Método de Elementos Finitos Aumentados, cuyo objetivo era modelar las discontinuidades débiles y fuertes sin necesidad de DoF adicionales, como afirmó PuM.

CorteFEM

El método de elementos finitos de corte se desarrolló en 2014. ^[15] El enfoque es "hacer que la discretización sea lo más independiente posible de la descripción geométrica y minimizar la complejidad de la generación de malla, al tiempo que se conserva la precisión y la solidez de un método de elementos finitos estándar". ^[16]

Método de elementos finitos generalizado

El método de elementos finitos generalizados (GFEM) utiliza espacios locales que consisten en funciones, no necesariamente polinomios, que reflejan la información disponible sobre la solución desconocida y, por lo tanto, garantizan una buena aproximación local. Luego, se utiliza una partición de unidad para “unir” estos espacios y formar el subespacio de aproximación. La eficacia del GFEM se ha demostrado cuando se aplica a problemas con dominios que tienen límites complicados, problemas con microescalas y problemas con capas límite. ^[17]

Método de elementos finitos mixtos

El método de elementos finitos mixtos es un tipo de método de elementos finitos en el que se introducen variables independientes adicionales como variables nodales durante la discretización de un problema de ecuación diferencial parcial.

Variable – polinomio

El hp-FEM combina de forma adaptativa elementos con tamaño variable h y grado polinomial p para lograr tasas de convergencia exponencial excepcionalmente rápidas. ^[18]

hpk-FEM

El hpk-FEM combina de forma adaptativa elementos con tamaño variable h , grado polinomial de las aproximaciones locales p y diferenciabilidad global de las aproximaciones locales ( k -1) para lograr las mejores tasas de convergencia.

XFEM

El método de elementos finitos extendido (XFEM) es una técnica numérica basada en el método de elementos finitos generalizados (GFEM) y el método de partición de la unidad (PUM). Extiende el método de elementos finitos clásico al enriquecer el espacio de soluciones para soluciones de ecuaciones diferenciales con funciones discontinuas. Los métodos de elementos finitos extendidos enriquecen el espacio de aproximación para reproducir de forma natural la característica desafiante asociada con el problema de interés: la discontinuidad, la singularidad, la capa límite, etc. Se demostró que para algunos problemas, tal incrustación de la característica del problema en el espacio de aproximación puede mejorar significativamente las tasas de convergencia y la precisión. Además, tratar problemas con discontinuidades con XFEM suprime la necesidad de mallar y volver a mallar las superficies de discontinuidad, aliviando así los costos computacionales y los errores de proyección asociados con los métodos de elementos finitos convencionales a costa de restringir las discontinuidades a los bordes de la malla.

Varios códigos de investigación implementan esta técnica en diversos grados:

1. ObtenerFEM++
2. xfem++
3. abiertoxfem++

XFEM también se ha implementado en códigos como Altair Radios, ASTER, Morfeo y Abaqus. Cada vez lo adopta más otro software comercial de elementos finitos, con algunos complementos e implementaciones básicas disponibles (ANSYS, SAMCEF, OOFELIE, etc.).

Método de elementos finitos de límite escalado (SBFEM)

El método de elementos finitos de contorno escalado (SBFEM) fue introducido por Song y Wolf (1997). ^[19] El SBFEM ha sido una de las contribuciones más provechosas en el área de análisis numérico de problemas de mecánica de fracturas. Es un método semianalítico sin solución fundamental que combina las ventajas de las formulaciones y procedimientos de elementos finitos y la discretización de elementos de contorno. Sin embargo, a diferencia del método de elementos de contorno, no se requiere una solución diferencial fundamental.

S-FEM

El método de elementos finitos suavizados (S-FEM) es una clase particular de algoritmos de simulación numérica para la simulación de fenómenos físicos. Se desarrolló combinando métodos sin malla con el método de elementos finitos.

Método de elementos espectrales

Los métodos de elementos espectrales combinan la flexibilidad geométrica de los elementos finitos y la precisión de los métodos espectrales. Los métodos espectrales son la solución aproximada de ecuaciones parciales de forma débil basadas en interpoladores lagrangianos de orden superior y se utilizan únicamente con ciertas reglas de cuadratura. ^[20]

Métodos sin malla

Métodos de Galerkin discontinuos

Análisis de límite de elementos finitos

Método de cuadrícula estirada

Iteración de Loubignac

La iteración de Loubignac es un método iterativo en los métodos de elementos finitos.

Método de elementos finitos de plasticidad cristalina (CPFEM)

El método de elementos finitos de plasticidad cristalina (CPFEM) es una herramienta numérica avanzada desarrollada por Franz Roters. Los metales pueden considerarse como agregados cristalinos, que se comportan de forma anisotrópica bajo deformación, como la localización anormal de tensiones y deformaciones. El CPFEM, basado en el deslizamiento (velocidad de deformación por cizallamiento), puede calcular la dislocación, la orientación del cristal y otra información de textura para considerar la anisotropía del cristal durante la rutina. Se ha aplicado en el estudio numérico de la deformación de materiales, la rugosidad de la superficie, las fracturas, etc.

Método de elementos virtuales (VEM)

El método de elementos virtuales (VEM), introducido por Beirão da Veiga et al. (2013) ^[21] como una extensión de los métodos de diferencias finitas miméticas (MFD), es una generalización del método de elementos finitos estándar para geometrías de elementos arbitrarios. Esto permite la admisión de polígonos generales (o poliedros en 3D) que son altamente irregulares y no convexos en forma. El nombre virtual deriva del hecho de que no se requiere el conocimiento de la base de la función de forma local y, de hecho, nunca se calcula explícitamente.

Enlace con el método de discretización de gradientes

Algunos tipos de métodos de elementos finitos (métodos de elementos finitos conformes, no conformes y mixtos) son casos particulares del método de discretización de gradiente (GDM). Por lo tanto, las propiedades de convergencia del GDM, que se establecen para una serie de problemas (problemas elípticos lineales y no lineales, problemas parabólicos lineales, no lineales y degenerados), también se cumplen para estos FEM particulares.

Comparación con el método de diferencias finitas

El método de diferencias finitas (MDF) es una forma alternativa de aproximar soluciones de ecuaciones en derivadas parciales. Las diferencias entre el MDF y el MDF son:

• La característica más atractiva del método FEM es su capacidad de manejar geometrías (y límites) complicadas con relativa facilidad. Mientras que el método FDM en su forma básica está restringido al manejo de formas rectangulares y modificaciones simples de las mismas, el manejo de geometrías en el método FEM es teóricamente sencillo. ^{[3] [22]}
• El FDM no suele utilizarse para geometrías CAD irregulares, sino más a menudo para modelos rectangulares o en forma de bloque. ^[23]
• El método FEM generalmente permite una adaptabilidad de malla más flexible que el FDM. ^[22]
• La característica más atractiva de las diferencias finitas es que son fáciles de implementar. ^[22]
• Se podría considerar el método FDM como un caso particular del método FEM de varias maneras. Por ejemplo, el método FEM de primer orden es idéntico al método FDM para la ecuación de Poisson si el problema se discretiza mediante una malla rectangular regular con cada rectángulo dividido en dos triángulos.
• Hay razones para considerar que la base matemática de la aproximación de elementos finitos es más sólida, por ejemplo, porque la calidad de la aproximación entre los puntos de la cuadrícula es pobre en FDM.
• La calidad de una aproximación FEM suele ser mayor que la del enfoque FDM correspondiente, pero esto depende en gran medida del problema y se pueden proporcionar varios ejemplos de lo contrario.

En general, el método de elementos finitos ( FEM) es el método de elección en todos los tipos de análisis en mecánica estructural (es decir, resolución de deformaciones y tensiones en cuerpos sólidos o dinámica de estructuras). Por el contrario, la dinámica de fluidos computacional (CFD) tiende a utilizar FDM u otros métodos como el método de volúmenes finitos (FVM). Los problemas de CFD suelen requerir la discretización del problema en una gran cantidad de celdas/puntos de cuadrícula (millones y más). Por lo tanto, el costo de la solución favorece una aproximación más simple y de orden inferior dentro de cada celda. Esto es especialmente cierto para los problemas de "flujo externo", como el flujo de aire alrededor del automóvil, el avión o la simulación meteorológica.

Métodos de elementos finitos y transformada rápida de Fourier (FFT)

Otro método utilizado para aproximar soluciones a una ecuación diferencial parcial es la Transformada Rápida de Fourier (FFT), donde la solución se aproxima mediante una serie de Fourier calculada utilizando la FFT. Para aproximar la respuesta mecánica de materiales bajo tensión, la FFT es a menudo mucho más rápida, ^[24] pero el FEM puede ser más preciso. ^[25] Un ejemplo de las respectivas ventajas de los dos métodos es en la simulación del laminado de una lámina de aluminio (un metal FCC) y el trefilado de un alambre de tungsteno (un metal BCC). Esta simulación no tenía un algoritmo sofisticado de actualización de forma para el método FFT. En ambos casos, el método FFT fue más de 10 veces más rápido que el FEM, pero en la simulación del trefilado, donde hubo grandes deformaciones en los granos , el método FEM fue mucho más preciso. En la simulación del laminado de láminas, los resultados de los dos métodos fueron similares. ^[25] La FFT tiene una mayor ventaja de velocidad en los casos en que las condiciones de contorno se dan en la deformación del material , y pierde parte de su eficiencia en los casos en que se utiliza la tensión para aplicar las condiciones de contorno, ya que se necesitan más iteraciones del método. ^[26]

Los métodos de FE y FFT también se pueden combinar en un método basado en vóxeles (2) para simular la deformación en materiales, donde el método de FE se utiliza para la tensión y la deformación a macroescala, y el método de FFT se utiliza en la microescala para tratar los efectos de la microescala en la respuesta mecánica. ^[27] A diferencia de FEM, las similitudes de los métodos de FFT con los métodos de procesamiento de imágenes significan que una imagen real de la microestructura de un microscopio se puede introducir en el solucionador para obtener una respuesta de tensión más precisa. El uso de una imagen real con FFT evita el mallado de la microestructura, que sería necesario si se utiliza la simulación FEM de la microestructura, y podría ser difícil. Debido a que las aproximaciones de Fourier son inherentemente periódicas, FFT solo se puede utilizar en casos de microestructura periódica, pero esto es común en materiales reales. ^[27] FFT también se puede combinar con métodos FEM utilizando componentes de Fourier como base variacional para aproximar los campos dentro de un elemento, lo que puede aprovechar la velocidad de los solucionadores basados ​​en FFT. ^[28]

Solicitud

Modelo 3D de transporte de contaminación: campo de concentración a nivel del suelo

Modelo 3D de transporte de contaminación: campo de concentración en una superficie perpendicular

Varias especializaciones bajo el paraguas de la disciplina de ingeniería mecánica (como las industrias aeronáutica, biomecánica y automotriz) utilizan comúnmente el método FEM integrado en el diseño y desarrollo de sus productos. Varios paquetes FEM modernos incluyen componentes específicos como entornos de trabajo térmicos, electromagnéticos, de fluidos y estructurales. En una simulación estructural, el método FEM ayuda enormemente a producir visualizaciones de rigidez y resistencia y a minimizar el peso, los materiales y los costos. ^[29]

El método FEM permite visualizar en detalle dónde se doblan o tuercen las estructuras, lo que indica la distribución de tensiones y desplazamientos. El software FEM proporciona una amplia gama de opciones de simulación para controlar la complejidad del modelado y el análisis del sistema. De manera similar, el nivel deseado de precisión requerido y los requisitos de tiempo computacional asociados se pueden gestionar simultáneamente para abordar la mayoría de las aplicaciones de ingeniería. El método FEM permite construir, refinar y optimizar diseños completos antes de fabricar el diseño. La malla es una parte integral del modelo y debe controlarse cuidadosamente para obtener los mejores resultados. En general, cuanto mayor sea el número de elementos en una malla, más precisa será la solución del problema discretizado. Sin embargo, existe un valor en el que los resultados convergen y un mayor refinamiento de la malla no aumenta la precisión. ^[30]

Modelo de elementos finitos de una articulación de rodilla humana ^[31]

Esta poderosa herramienta de diseño ha mejorado significativamente tanto el estándar de los diseños de ingeniería como la metodología del proceso de diseño en muchas aplicaciones industriales. ^[32] La introducción del método de elementos finitos ha disminuido sustancialmente el tiempo necesario para llevar los productos desde el concepto hasta la línea de producción. ^[32] Las pruebas y el desarrollo se han acelerado principalmente a través de diseños de prototipos iniciales mejorados utilizando el método de elementos finitos. ^[33] En resumen, los beneficios del método de elementos finitos incluyen mayor precisión, diseño mejorado y mejor conocimiento de los parámetros de diseño críticos, creación de prototipos virtuales, menos prototipos de hardware, un ciclo de diseño más rápido y menos costoso, mayor productividad y mayores ingresos. ^[32]

En la década de 1990 se propuso el uso del método FEM en modelos estocásticos para resolver numéricamente modelos de probabilidad ^[34] y más tarde para la evaluación de la confiabilidad. ^[35]

El método FEM se aplica ampliamente para aproximar ecuaciones diferenciales que describen sistemas físicos. Este método es muy popular en la comunidad de dinámica de fluidos computacional , y existen muchas aplicaciones para resolver ecuaciones de Navier-Stokes con FEM. ^{[36] [37] [38]} Recientemente, la aplicación de FEM ha ido en aumento en las investigaciones del plasma computacional. Se han propuesto resultados numéricos prometedores utilizando FEM para magnetohidrodinámica , ecuación de Vlasov y ecuación de Schrödinger . ^{[39] [40]}

Véase también

• Método de elementos aplicados
• Método de elementos de contorno
• Lema de Céa
• Experimento informático
• Método de rigidez directa
• Optimización del diseño de discontinuidades
• Método de elementos discretos
• Método de diferencias finitas
• Máquina de elementos finitos
• Método de elementos finitos en mecánica estructural
• Método de volumen finito
• Método de volumen finito para flujo inestable
• Método de elementos infinitos
• Elemento finito de intervalo
• Análisis isogeométrico
• Métodos de Boltzmann en red
• Lista de paquetes de software de elementos finitos
• Métodos sin malla
• Autómata celular móvil
• Optimización del diseño multidisciplinario
• Multifísica
• Prueba de parche
• Método Rayleigh-Ritz
• Mapeo espacial
• HILO 7
• Teselación (gráficos por computadora)
• Forma débil debilitada

Referencias

1. Hoang, Viet Ha; Schwab, Christoph (2005). "Elementos finitos de alta dimensión para problemas elípticos con múltiples escalas". Modelado y simulación multiescala . 3 (1). SIAM: 168–194. doi :10.1137/040606041.
2. Daryl L. Logan (2011). Un primer curso sobre el método de elementos finitos . Cengage Learning. ISBN 9780495668275.
3. Reddy, JN (2006). Introducción al método de elementos finitos (tercera edición). McGraw-Hill. ISBN 9780071267618.
4. Huebner, Kenneth H. (2001). El método de elementos finitos para ingenieros . Wiley. ISBN 978-0-471-37078-9.
5. Liu, Wing Kam; Li, Shaofan; Park, Harold S. (2022). "Ochenta años del método de elementos finitos: nacimiento, evolución y futuro". Archivos de métodos computacionales en ingeniería . 29 (6): 4431–4453. arXiv : 2107.04960 . doi : 10.1007/s11831-022-09740-9 . ISSN  1134-3060. S2CID  235794921.
6. Hrennikoff, Alexander (1941). "Solución de problemas de elasticidad por el método del marco". Journal of Applied Mechanics . 8 (4): 169–175. Bibcode :1941JAM.....8A.169H. doi :10.1115/1.4009129.
7. Courant, R. (1943). "Métodos variacionales para la solución de problemas de equilibrio y vibraciones". Boletín de la Sociedad Matemática Americana . 49 : 1–23. doi : 10.1090/s0002-9904-1943-07818-4 .
8. "СПб ЭМИ РАН". emi.nw.ru . Archivado desde el original el 30 de septiembre de 2015 . Consultado el 17 de marzo de 2018 .
9. Hinton, Ernest; Irons, Bruce (julio de 1968). "Suavizado de datos experimentales mediante mínimos cuadrados utilizando elementos finitos". Strain . 4 (3): 24–27. doi :10.1111/j.1475-1305.1968.tb01368.x.
10. "Software y manuales SAP-IV". Biblioteca electrónica NISEE, Archivo en línea de ingeniería sísmica. Archivado desde el original el 9 de marzo de 2013. Consultado el 24 de enero de 2013 .
11. Gard Paulsen; Håkon con Andersen; John Petter Collett; Iver Tangen Stensrud (2014). Construyendo confianza, La historia de DNV 1864-2014 . Lysaker, Noruega: Dinamo Forlag A/S. págs.121, 436. ISBN 978-82-8071-256-1.
12. Strang, Gilbert ; Fix, George (1973). Un análisis del método de elementos finitos . Prentice Hall. ISBN 978-0-13-032946-2.
13. Olek C Zienkiewicz; Robert L Taylor; JZ Zhu (31 de agosto de 2013). El método de elementos finitos: su base y fundamentos. Butterworth-Heinemann. ISBN 978-0-08-095135-5.
14. Bathe, KJ (2006). Procedimientos de elementos finitos . Cambridge, MA: Klaus-Jürgen Bathe. ISBN 978-0979004902.
15. celledoni (27 de febrero de 2023). "CutFEM: discretización de ecuaciones diferenciales parciales y geometría". ECMI . Consultado el 13 de octubre de 2023 .
16. Burman, Erik; Claus, Susanne; Hansbo, Peter; Larson, Mats G.; Massing, André (16 de noviembre de 2015). "CutFEM: Discretización de geometría y ecuaciones diferenciales parciales". Revista internacional de métodos numéricos en ingeniería . 104 (7): 472–501. Bibcode :2015IJNME.104..472B. doi : 10.1002/nme.4823 . ISSN  0029-5981.
17. Babuška, Ivo ; Banerjee, Uday; Osborn, John E. (junio de 2004). "Métodos de elementos finitos generalizados: ideas principales, resultados y perspectiva". Revista internacional de métodos computacionales . 1 (1): 67–103. doi :10.1142/S0219876204000083.
18. P. Solin, K. Segeth, I. Dolezel: Métodos de elementos finitos de orden superior, Chapman & Hall/CRC Press, 2003
19. Song, Chongmin; Wolf, John P. (5 de agosto de 1997). "El método de elementos finitos de límite escalado – también conocido como método de celdas de elementos finitos infinitesimales consistentes – para la elastodinámica". Métodos informáticos en mecánica aplicada e ingeniería . 147 (3–4): 329–355. Bibcode :1997CMAME.147..329S. doi :10.1016/S0045-7825(97)00021-2.
20. "Métodos de elementos espectrales". Laboratorio Estatal Clave de Informática Científica e Ingeniería . Archivado desde el original el 10 de agosto de 2017. Consultado el 28 de julio de 2017 .
21. Beirão da Veiga, L.; Brezzi, F.; Cangiani, A.; Manzini, G.; Marini, LD; Russo, A. (2013). "Principios básicos de los métodos de elementos virtuales". Modelos y métodos matemáticos en ciencias aplicadas . 23 (1): 199–214. doi :10.1142/S0218202512500492.
22. Topper, Jürgen (enero de 2005). "Fijación de precios de opciones con elementos finitos". Wilmott . 2005 (1): 84–90. doi :10.1002/wilm.42820050119 (inactivo 2024-04-07). ISSN  1540-6962.{{cite journal}}: CS1 maint: DOI inactive as of April 2024 (link)
23. "¿Cuál es la diferencia entre FEM, FDM y FVM?". Diseño de máquinas . 2016-04-18. Archivado desde el original el 2017-07-28 . Consultado el 2017-07-28 .
24. Ma, X; Parvathaneni, K; Lomov, S; Vasiukov, D; Shakoor, M; Park, C (diciembre de 2019). "Comparación cuantitativa entre la transformada rápida de Fourier y el método de elementos finitos para el modelado micromecánico de materiales compuestos". Conferencia FiBreMoD .
25. Prakash, A; Lebensohn, RA (1 de septiembre de 2009). "Simulación del comportamiento micromecánico de policristales: elementos finitos frente a transformadas rápidas de Fourier". Modelado y simulación en ciencia e ingeniería de materiales . 17 (6): 064010. Bibcode :2009MSMSE..17f4010P. doi :10.1088/0965-0393/17/6/064010. ISSN  0965-0393.
26. Cruzado, A; Segurado, J; Hartl, DJ; Benzerga, AA (2021-06-01). "Un método de transformada rápida de Fourier variacional para materiales que transforman fases". Modelado y simulación en ciencia e ingeniería de materiales . 29 (4): 045001. Bibcode :2021MSMSE..29d5001C. doi :10.1088/1361-651X/abe4c7. ISSN  0965-0393.
27. Gierden, Christian; Kochmann, Julian; Waimann, Johanna; Svendsen, Bob; Reese, Stefanie (1 de octubre de 2022). "Una revisión de los métodos de dos escalas basados ​​en FE-FFT para el modelado computacional de la evolución de la microestructura y el comportamiento macroscópico de los materiales". Archivos de métodos computacionales en ingeniería . 29 (6): 4115–4135. doi : 10.1007/s11831-022-09735-6 . ISSN  1886-1784.
28. Zeman, J.; de Geus, TWJ; Vondřejc, J.; Peerlings, RHJ; Geers, MGD (7 de septiembre de 2017). "Una perspectiva de elementos finitos sobre simulaciones micromecánicas no lineales basadas en FFT: UNA PERSPECTIVA DE ELEMENTOS FINITOS EN SIMULACIONES NO LINEALES BASADAS EN FFT". Revista internacional de métodos numéricos en ingeniería . 111 (10): 903–926. arXiv : 1601.05970 . doi :10.1002/nme.5481.
29. Kiritsis, D.; Eemmanouilidis, Ch.; Koronios, A.; Mathew, J. (2009). "Gestión de activos de ingeniería". Actas del 4.º Congreso Mundial sobre Gestión de Activos de Ingeniería (WCEAM) : 591–592.
30. "Análisis de elementos finitos: cómo crear un gran modelo". Coventive Composites . 2019-03-18 . Consultado el 2019-04-05 .^{[ enlace muerto permanente ]}
31. Naghibi Beidokhti, Hamid; Janssen, Dennis; Khoshgoftar, Mehdi; Sprengers, Andre; Perdahcioglu, Emin Semih; Boogaard, Ton Van den; Verdonschot, Nico (2016). "Una comparación entre simulaciones dinámicas implícitas y explícitas de elementos finitos de la articulación de la rodilla nativa" (PDF) . Ingeniería médica y física . 38 (10): 1123–1130. doi :10.1016/j.medengphy.2016.06.001. PMID  27349493. Archivado (PDF) desde el original el 2018-07-19 . Consultado el 2019-09-19 .
32. Hastings, JK, Juds, MA, Brauer, JR, Precisión y economía del análisis magnético de elementos finitos , 33.ª Conferencia Nacional Anual de Relevos, abril de 1985.
33. McLaren-Mercedes (2006). "McLaren Mercedes: Feature - Stress to impress". Archivado desde el original el 2006-10-30 . Consultado el 2006-10-03 .
34. Peng Long; Wang Jinliang; Zhu Qiding (19 de mayo de 1995). "Métodos con alta precisión para el cálculo de probabilidad de elementos finitos". Revista de Matemática Computacional y Aplicada . 59 (2): 181–189. doi :10.1016/0377-0427(94)00027-X.
35. Haldar, Achintya; Mahadevan, Sankaran (2000). Evaluación de la confiabilidad mediante análisis de elementos finitos estocásticos . John Wiley & Sons. ISBN 978-0471369615.
36. Girault, Vivette; Raviart, Pierre-Arnaud (1979). Aproximación de elementos finitos de las ecuaciones de Navier-Stokes . Vol. 749. Springer Berlin. ISBN 978-3-540-09557-6.
37. Cuvelier, Cornelis; Segal, agosto; Van Steenhoven, Antón A (1986). Métodos de elementos finitos y ecuaciones de Navier-Stokes . vol. 22. Medios científicos y comerciales de Springer. ISBN 978-1-4020-0309-7.
38. Girault, Vivette; Raviart, Pierre-Arnaud (2012). Métodos de elementos finitos para ecuaciones de Navier-Stokes: teoría y algoritmos . Vol. 5. Springer Science & Business Media. ISBN 978-3-642-64888-5.
39. Karakashian, Ohannes; Makridakis, Charalambos (1999). "Un método de elementos finitos de espacio-tiempo para la ecuación no lineal de Schrödinger: el método continuo de Galerkin". Revista SIAM sobre análisis numérico . 36 (6). SIAM: 1779–1807. doi :10.1016/0377-0427(94)00027-X.
40. Sovinec, Carl R.; Glasser, AH; Gianakon, TA; Barnes, DC; Nebel, RA; Kruger, SE; Schnack, DD; Plimpton, SJ; Tarditi, A.; Chu, MS (2004). "Simulación magnetohidrodinámica no lineal utilizando elementos finitos de alto orden". Journal of Computational Physics . 195 (1). Elsevier: 355–386. doi :10.1016/j.jcp.2003.10.004.

Lectura adicional

• G. Allaire y A. Craig: Análisis numérico y optimización: una introducción al modelado matemático y la simulación numérica .
• KJ Bathe: Métodos numéricos en el análisis de elementos finitos , Prentice-Hall (1976).
• Thomas JR Hughes: El método de elementos finitos: análisis de elementos finitos estáticos y dinámicos lineales, Prentice-Hall (1987).
• J. Chaskalovic: Métodos de elementos finitos para ciencias de ingeniería , Springer Verlag, (2008).
• Endre Süli : Métodos de elementos finitos para ecuaciones diferenciales parciales.
• OC Zienkiewicz, RL Taylor, JZ Zhu: El método de elementos finitos: su base y fundamentos , Butterworth-Heinemann (2005).
• N. Ottosen, H. Petersson: Introducción al método de elementos finitos, Prentice-Hall (1992).
• Susanne C. Brenner, L. Ridgway Scott: La teoría matemática de los métodos de elementos finitos , Springer-Verlag Nueva York, ISBN 978-0-387-75933-3 (2008).
• Zohdi, TI (2018) Una introducción a los elementos finitos para principiantes: versión ampliada que incluye ejemplos de pruebas y proyectos. Segunda edición https://link.springer.com/book/10.1007/978-3-319-70428-9
• Leszek F. Demkowicz: Teoría matemática de elementos finitos , SIAM, ISBN 978-1-61197-772-1 (2024).