Espectroscopia rotacional

Espectroscopia de estados rotacionales cuantificados de gases

Parte del espectro rotacional del trifluoroyodometano , CF
₃I . ^{[notas 1]} Cada transición rotacional está etiquetada con los números cuánticos, J , de los estados final e inicial, y está ampliamente dividida por los efectos del acoplamiento cuadrupolo nuclear con el núcleo ¹²⁷ I.

La espectroscopia rotacional se ocupa de la medición de las energías de las transiciones entre estados rotacionales cuantizados de moléculas en la fase gaseosa . El espectro rotacional ( densidad espectral de potencia vs. frecuencia rotacional ) de moléculas polares se puede medir en absorción o emisión mediante espectroscopia de microondas ^[1] o mediante espectroscopia de infrarrojo lejano . Los espectros rotacionales de moléculas no polares no se pueden observar mediante esos métodos, pero se pueden observar y medir mediante espectroscopia Raman . La espectroscopia rotacional a veces se denomina espectroscopia rotacional pura para distinguirla de la espectroscopia rotacional-vibratoria, donde los cambios en la energía rotacional ocurren junto con los cambios en la energía vibracional, y también de la espectroscopia ro-vibrónica (o simplemente espectroscopia vibrónica ), donde los cambios de energía rotacional, vibracional y electrónica ocurren simultáneamente.

Para la espectroscopia rotacional, las moléculas se clasifican según su simetría en cimas esféricas, moléculas lineales y cimas simétricas; se pueden derivar expresiones analíticas para los términos de energía rotacional de estas moléculas. Se pueden derivar expresiones analíticas para la cuarta categoría, cima asimétrica, para niveles rotacionales de hasta J=3, pero los niveles de energía más altos deben determinarse utilizando métodos numéricos. Las energías rotacionales se derivan teóricamente considerando que las moléculas son rotores rígidos y luego aplicando términos adicionales para tener en cuenta la distorsión centrífuga , la estructura fina , la estructura hiperfina y el acoplamiento de Coriolis . El ajuste de los espectros a las expresiones teóricas proporciona valores numéricos de los momentos angulares de inercia a partir de los cuales se pueden derivar valores muy precisos de longitudes y ángulos de enlace molecular en casos favorables. En presencia de un campo electrostático hay una división de Stark que permite determinar los momentos dipolares eléctricos moleculares.

Una aplicación importante de la espectroscopia rotacional es la exploración de la composición química del medio interestelar utilizando radiotelescopios .

Aplicaciones

La espectroscopia rotacional se ha utilizado principalmente para investigar aspectos fundamentales de la física molecular. Es una herramienta excepcionalmente precisa para la determinación de la estructura molecular en moléculas en fase gaseosa. Se puede utilizar para establecer barreras a la rotación interna, como la asociada con la rotación del CH
₃grupo relativo al C
₆yo
₄Grupo Cl en clorotolueno ( C
₇yo
₇Cl ). ^[2] Cuando se puede observar una estructura fina o hiperfina, la técnica también proporciona información sobre las estructuras electrónicas de las moléculas. Gran parte de la comprensión actual de la naturaleza de las interacciones moleculares débiles, como los enlaces de van der Waals , de hidrógeno y de halógeno, se ha establecido mediante espectroscopia rotacional. En relación con la radioastronomía , la técnica tiene un papel clave en la exploración de la composición química del medio interestelar . Las transiciones de microondas se miden en el laboratorio y se comparan con las emisiones del medio interestelar utilizando un radiotelescopio . NH3Fue la primera molécula poliatómica estable identificada en el medio interestelar . ^[3] La medición del monóxido de cloro ^[4] es importante para la química atmosférica . Los proyectos actuales en astroquímica involucran tanto la espectroscopia de microondas de laboratorio como las observaciones realizadas con radiotelescopios modernos como el Atacama Large Millimeter/submillimeter Array (ALMA). ^[5]

Descripción general

Una molécula en fase gaseosa puede rotar libremente respecto de un conjunto de ejes ortogonales entre sí y de orientación fija en el espacio, centrados en el centro de masa de la molécula. La rotación libre no es posible para las moléculas en fase líquida o sólida debido a la presencia de fuerzas intermoleculares . La rotación sobre cada eje único está asociada a un conjunto de niveles de energía cuantizados que dependen del momento de inercia sobre ese eje y de un número cuántico. Por lo tanto, para las moléculas lineales, los niveles de energía se describen mediante un único momento de inercia y un único número cuántico, , que define la magnitud del momento angular rotacional. ${\displaystyle J}$

En el caso de moléculas no lineales que son rotores simétricos (o trompos simétricos, véase la siguiente sección), existen dos momentos de inercia y la energía también depende de un segundo número cuántico rotacional, , que define el componente vectorial del momento angular rotacional a lo largo del eje de simetría principal . ^[6] El análisis de datos espectroscópicos con las expresiones detalladas a continuación da como resultado la determinación cuantitativa del valor o los valores del momento o los momentos de inercia. A partir de estos, se pueden obtener valores precisos de la estructura y las dimensiones moleculares. ${\displaystyle K}$

Para una molécula lineal, el análisis del espectro rotacional proporciona valores para la constante rotacional ^{[notas 2]} y el momento de inercia de la molécula y, conociendo las masas atómicas, se puede utilizar para determinar la longitud de enlace directamente. Para las moléculas diatómicas este proceso es sencillo. Para las moléculas lineales con más de dos átomos es necesario medir los espectros de dos o más isotólogos , como ¹⁶ O ¹² C ³² S y ¹⁶ O ¹² C ³⁴ S. Esto permite establecer y resolver un conjunto de ecuaciones simultáneas para las longitudes de enlace ). ^{[notas 3]} Una longitud de enlace obtenida de esta manera es ligeramente diferente de la longitud de enlace de equilibrio. Esto se debe a que hay energía de punto cero en el estado fundamental vibracional, al que se refieren los estados rotacionales, mientras que la longitud de enlace de equilibrio está en el mínimo en la curva de energía potencial. La relación entre las constantes rotacionales está dada por

${\displaystyle B_{v}=B-\alpha \left(v+{\frac {1}{2}}\right)}$

donde v es un número cuántico vibracional y α es una constante de interacción vibración-rotación que se puede calcular si se pueden encontrar los valores B para dos estados vibracionales diferentes. ^[7]

En el caso de otras moléculas, si se pueden resolver los espectros y asignar transiciones individuales a las longitudes y ángulos de enlace , se pueden deducir. Cuando esto no es posible, como ocurre con la mayoría de los topes asimétricos, todo lo que se puede hacer es ajustar los espectros a tres momentos de inercia calculados a partir de una estructura molecular supuesta. Al variar la estructura molecular, se puede mejorar el ajuste, lo que da una estimación cualitativa de la estructura. La sustitución isotópica es inestimable cuando se utiliza este enfoque para la determinación de la estructura molecular.

Clasificación de rotores moleculares

En mecánica cuántica la rotación libre de una molécula está cuantizada , de modo que la energía rotacional y el momento angular pueden tomar solo ciertos valores fijos, que están relacionados simplemente con el momento de inercia , , de la molécula. Para cualquier molécula, hay tres momentos de inercia: , y alrededor de tres ejes mutuamente ortogonales A , B , y C con el origen en el centro de masa del sistema. La convención general, utilizada en este artículo, es definir los ejes de manera que , con eje correspondiente al momento de inercia más pequeño. Algunos autores, sin embargo, definen el eje como el eje de rotación molecular de orden más alto. ${\displaystyle I}$ ${\displaystyle I_{A}}$ ${\displaystyle I_{B}}$ ${\displaystyle I_{C}}$ ${\displaystyle I_{A}\leq I_{B}\leq I_{C}}$ ${\displaystyle A}$ ${\displaystyle A}$

El patrón particular de niveles de energía (y, por lo tanto, de transiciones en el espectro rotacional) de una molécula está determinado por su simetría. Una forma conveniente de observar las moléculas es dividirlas en cuatro clases diferentes, según la simetría de su estructura. Estas son:

Rotores esféricos

Los tres momentos de inercia son iguales entre sí: . Entre los ejemplos de peonzas esféricas se incluyen el tetrámero de fósforo ( P ${\displaystyle I_{A}=I_{B}=I_{C}}$4) , tetracloruro de carbono ( CCl
₄) y otros tetrahaluros, metano ( CH
₄) , silano, ( SiH
₄) , hexafluoruro de azufre ( SF
₆) y otros hexahaluros. Todas las moléculas pertenecen a los grupos puntuales cúbicos T _d o _Oh .

Moléculas lineales

Para una molécula lineal, los momentos de inercia están relacionados por . Para la mayoría de los propósitos, se puede tomar como cero. Los ejemplos de moléculas lineales incluyen dioxígeno ( O ${\displaystyle I_{A}\ll I_{B}=I_{C}}$ ${\displaystyle I_{A}}$2) , dinitrógeno ( N
₂) , monóxido de carbono (CO) , radical hidroxi (OH) , dióxido de carbono (CO ₂ ) , cianuro de hidrógeno (HCN) , sulfuro de carbonilo (OCS) , acetileno (etino (HC≡CH) y dihaloetinos. Estas moléculas pertenecen a los grupos puntuales C _∞v o D _∞h .

Rotores simétricos

Un trompo simétrico es una molécula en la que dos momentos de inercia son iguales, o . Por definición, un trompo simétrico debe tener un eje de rotación de orden triple o superior . Por conveniencia, los espectroscopistas dividen las moléculas en dos clases de trompos simétricos, trompos simétricos achatados (con forma de platillo o disco) con y trompos simétricos alargados (con forma de balón de rugby o de cigarro) con . Los espectros se ven bastante diferentes y son reconocibles al instante. Algunos ejemplos de trompos simétricos incluyen ${\displaystyle I_{A}=I_{B}}$ ${\displaystyle I_{B}=I_{C}}$ ${\displaystyle I_{A}=I_{B}<I_{C}}$ ${\displaystyle I_{A}<I_{B}=I_{C}}$

Oblato

Benceno, C
₆yo
₆; amoniaco, NH
₃; tetrafluoruro de xenón, XeF
₄

Prolapso

Clorometano, CH
₃Cl , propino, CH
₃C≡CH

Como ejemplo detallado, el amoniaco tiene un momento de inercia I _C = 4,4128 × 10 ⁻⁴⁷ kg m ² alrededor del eje de rotación triple, y momentos I _A = I _B = 2,8059 × 10 ⁻⁴⁷ kg m ² alrededor de cualquier eje perpendicular al eje C ₃ . Dado que el único momento de inercia es mayor que los otros dos, la molécula es una parte superior simétrica achatada. ^[8]

Tapas asimétricas (rotores asimétricos)

Los tres momentos de inercia tienen valores diferentes. Entre los ejemplos de moléculas pequeñas que tienen cimas asimétricas se incluyen el agua, el H
₂O y dióxido de nitrógeno, NO
₂cuyo eje de simetría de orden más alto es un eje de rotación doble. La mayoría de las moléculas grandes tienen cimas asimétricas.

Reglas de selección

Espectros de microondas e infrarrojo lejano

Se pueden observar transiciones entre estados rotacionales en moléculas con un momento dipolar eléctrico permanente . ^{[9] [notas 4]} Una consecuencia de esta regla es que no se puede observar ningún espectro de microondas para moléculas lineales centrosimétricas como N
₂( dinitrogeno ) o HCCH ( etino ), que son no polares. Moléculas tetraédricas como CH
₄( metano ), que tiene un momento dipolar cero y una polarizabilidad isotrópica, no tendría un espectro de rotación puro si no fuera por el efecto de la distorsión centrífuga; cuando la molécula gira alrededor de un eje de simetría triple, se crea un momento dipolar pequeño, lo que permite observar un espectro de rotación débil mediante espectroscopia de microondas. ^[10]

Con cimas simétricas, la regla de selección para transiciones de rotación pura permitidas por dipolo eléctrico es Δ K = 0 , Δ J = ±1 . Dado que estas transiciones se deben a la absorción (o emisión) de un solo fotón con un espín de uno, la conservación del momento angular implica que el momento angular molecular puede cambiar como máximo en una unidad. ^[11] Además, el número cuántico K está limitado a tener valores entre + J y - J , ambos inclusive . ^[12]

Espectros Raman

Para los espectros Raman, las moléculas experimentan transiciones en las que se absorbe un fotón incidente y se emite otro fotón dispersado . La regla de selección general para que se permita dicha transición es que la polarizabilidad molecular debe ser anisotrópica , lo que significa que no es la misma en todas las direcciones. ^{[13] La polarizabilidad es un} tensor tridimensional que se puede representar como un elipsoide. El elipsoide de polarizabilidad de las moléculas con cima esférica es de hecho esférico, por lo que esas moléculas no muestran un espectro Raman rotacional. Para todas las demás moléculas se pueden observar líneas de Stokes y anti-Stokes ^{[notas 5]} y tienen intensidades similares debido al hecho de que muchos estados rotacionales están poblados térmicamente. La regla de selección para moléculas lineales es ΔJ = 0, ±2. La razón de los valores ±2 es que la polarizabilidad vuelve al mismo valor dos veces durante una rotación. ^[14] El valor ΔJ = 0 no corresponde a una transición molecular sino a una dispersión de Rayleigh en la que el fotón incidente simplemente cambia de dirección. ^[15]

La regla de selección para moléculas superiores simétricas es

ΔK = 0

Si K = 0, entonces Δ J = ±2

Si K ≠ 0, entonces Δ J = 0, ±1, ±2

Se dice que las transiciones con Δ J = +1 pertenecen a la serie R , mientras que las transiciones con Δ J = +2 pertenecen a una serie S. ^[15] Dado que las transiciones Raman involucran dos fotones, es posible que el momento angular molecular cambie en dos unidades.

Unidades

Las unidades utilizadas para las constantes rotacionales dependen del tipo de medida. En el caso de los espectros infrarrojos en la escala de números de onda ( ), la unidad suele ser el centímetro inverso , escrito como cm ⁻¹ , que es literalmente el número de ondas en un centímetro, o el recíproco de la longitud de onda en centímetros ( ). Por otro lado, para los espectros de microondas en la escala de frecuencia ( ), la unidad suele ser el gigahercio . La relación entre estas dos unidades se deriva de la expresión ${\displaystyle {\tilde {\nu }}}$ ${\displaystyle {\tilde {\nu }}=1/\lambda }$ ${\displaystyle \nu }$

${\displaystyle \nu \cdot \lambda =c,}$

donde ν es una frecuencia , λ es una longitud de onda y c es la velocidad de la luz . De ello se deduce que

${\displaystyle {\tilde {\nu }}/{\text{cm}}^{-1}={\frac {1}{\lambda /{\text{cm}}}}={\frac {\nu /{\text{s}}^{-1}}{c/\left({\text{cm}}\cdot \mathrm {s} ^{-1}\right)}}={\frac {\nu /{\text{s}}^{-1}}{2.99792458\times 10^{10}}}.}$

Como 1 GHz = 10 ⁹ Hz, la conversión numérica se puede expresar como

${\displaystyle {\tilde {\nu }}/{\text{cm}}^{-1}\approx {\frac {\nu /{\text{GHz}}}{30}}.}$

Efecto de la vibración en la rotación

La población de estados vibracionales excitados sigue una distribución de Boltzmann , por lo que los estados vibracionales de baja frecuencia están poblados de manera apreciable incluso a temperatura ambiente. Como el momento de inercia es mayor cuando se excita una vibración, las constantes rotacionales ( B ) disminuyen. En consecuencia, las frecuencias de rotación en cada estado de vibración son diferentes entre sí. Esto puede dar lugar a líneas "satélite" en el espectro rotacional. Un ejemplo lo proporciona el cianodiacetileno , H−C≡C−C≡C−C≡N. ^[16]

Además, existe una fuerza ficticia , el acoplamiento de Coriolis , entre el movimiento vibracional de los núcleos en el marco rotatorio (no inercial). Sin embargo, mientras el número cuántico vibracional no cambie (es decir, la molécula está en un solo estado de vibración), el efecto de la vibración en la rotación no es importante, porque el tiempo para la vibración es mucho más corto que el tiempo requerido para la rotación. El acoplamiento de Coriolis también suele ser insignificante si uno está interesado solo en números cuánticos vibracionales y rotacionales bajos.

Efecto de la rotación sobre los espectros vibracionales

Históricamente, la teoría de los niveles de energía rotacional se desarrolló para explicar las observaciones de los espectros de vibración-rotación de los gases en la espectroscopia infrarroja , que se utilizaba antes de que la espectroscopia de microondas se volviera práctica. En una primera aproximación, la rotación y la vibración se pueden tratar como separables , por lo que la energía de rotación se suma a la energía de vibración. Por ejemplo, los niveles de energía rotacional para moléculas lineales (en la aproximación de rotor rígido) son

${\displaystyle E_{\text{rot}}=hcBJ(J+1).}$

En esta aproximación, los números de onda de vibración-rotación de las transiciones son

${\displaystyle {\tilde {\nu }}={\tilde {\nu }}_{\text{vib}}+B''J''(J''+1)-B'J'(J'+1),}$

donde y son constantes rotacionales para el estado vibracional superior e inferior respectivamente, mientras que y son los números cuánticos rotacionales de los niveles superior e inferior. En realidad, esta expresión debe modificarse para los efectos de la anarmonicidad de las vibraciones, la distorsión centrífuga y el acoplamiento de Coriolis. ^[17] ${\displaystyle B''}$ ${\displaystyle B'}$ ${\displaystyle J''}$ ${\displaystyle J'}$

Para la denominada rama R del espectro, de modo que se produce una excitación simultánea tanto de vibración como de rotación. Para la rama P , de modo que se pierde un cuanto de energía rotacional mientras se gana un cuanto de energía vibracional. La transición puramente vibracional, , da lugar a la rama Q del espectro. Debido a la población térmica de los estados rotacionales, la rama P es ligeramente menos intensa que la rama R. ${\displaystyle J'=J''+1}$ ${\displaystyle J'=J''-1}$ ${\displaystyle \Delta J=0}$

Las constantes rotacionales obtenidas a partir de mediciones infrarrojas concuerdan bien con las obtenidas mediante espectroscopia de microondas, aunque esta última suele ofrecer una mayor precisión.

Estructura de los espectros rotacionales

Parte superior esférica

Las moléculas con cima esférica no tienen momento dipolar neto. No se puede observar un espectro rotacional puro mediante espectroscopia de absorción o emisión porque no hay un momento dipolar permanente cuya rotación pueda ser acelerada por el campo eléctrico de un fotón incidente. Además, la polarizabilidad es isotrópica, de modo que tampoco se pueden observar transiciones rotacionales puras mediante espectroscopia Raman. Sin embargo, las constantes rotacionales se pueden obtener mediante espectroscopia ro-vibratoria . Esto ocurre cuando una molécula es polar en el estado vibracionalmente excitado. Por ejemplo, la molécula metano es una cima esférica pero la banda de estiramiento asimétrica CH muestra una estructura fina rotacional en el espectro infrarrojo, ilustrada en el acoplamiento rovibratorio . Este espectro también es interesante porque muestra evidencia clara de acoplamiento de Coriolis en la estructura asimétrica de la banda.

Moléculas lineales

Niveles de energía y posiciones de línea calculados en la aproximación de rotor rígido

El rotor rígido es un buen punto de partida para construir un modelo de una molécula rotatoria. Se supone que los átomos componentes son masas puntuales conectadas por enlaces rígidos. Una molécula lineal se encuentra sobre un solo eje y cada átomo se mueve sobre la superficie de una esfera alrededor del centro de masas. Los dos grados de libertad rotacional corresponden a las coordenadas esféricas θ y φ que describen la dirección del eje molecular, y el estado cuántico está determinado por dos números cuánticos J ​​y M. J define la magnitud del momento angular rotacional, y M su componente alrededor de un eje fijo en el espacio, como un campo eléctrico o magnético externo. En ausencia de campos externos, la energía depende solo de J. Bajo el modelo de rotor rígido , los niveles de energía rotacional, F (J), de la molécula se pueden expresar como,

${\displaystyle F\left(J\right)=BJ\left(J+1\right)\qquad J=0,1,2,...}$

donde es la constante rotacional de la molécula y está relacionada con el momento de inercia de la molécula. En una molécula lineal el momento de inercia alrededor de un eje perpendicular al eje molecular es único, es decir, , por lo que ${\displaystyle B}$ ${\displaystyle I_{B}=I_{C},I_{A}=0}$

${\displaystyle B={h \over {8\pi ^{2}cI_{B}}}={h \over {8\pi ^{2}cI_{C}}}}$

Para una molécula diatómica

${\displaystyle I={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}d^{2}}$

donde m ₁ y m ₂ son las masas de los átomos y d es la distancia entre ellos.

Las reglas de selección dictan que durante la emisión o absorción el número cuántico rotacional tiene que cambiar en la unidad, es decir, . Por lo tanto, las ubicaciones de las líneas en un espectro rotacional estarán dadas por ${\displaystyle \Delta J=J^{\prime }-J^{\prime \prime }=\pm 1}$

${\displaystyle {\tilde {\nu }}_{J^{\prime }\leftrightarrow J^{\prime \prime }}=F\left(J^{\prime }\right)-F\left(J^{\prime \prime }\right)=2B\left(J^{\prime \prime }+1\right)\qquad J^{\prime \prime }=0,1,2,...}$

donde denota el nivel inferior y denota el nivel superior involucrado en la transición. ${\displaystyle J^{\prime \prime }}$ ${\displaystyle J^{\prime }}$

El diagrama ilustra transiciones rotacionales que obedecen a la regla de selección =1. Las líneas discontinuas muestran cómo estas transiciones se asignan a características que se pueden observar experimentalmente. Las transiciones adyacentes están separadas por 2 B en el espectro observado. También se pueden utilizar unidades de frecuencia o número de onda para el eje x de este gráfico. ${\displaystyle \Delta J}$ ${\displaystyle J^{\prime \prime }{\leftarrow }J^{\prime }}$

Intensidades de línea rotacional

Poblaciones de nivel rotacional con Bhc / kT = 0,05. J es el número cuántico del estado rotacional inferior.

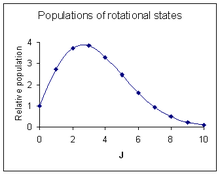
La probabilidad de que se produzca una transición es el factor más importante que influye en la intensidad de una línea de rotación observada. Esta probabilidad es proporcional a la población del estado inicial involucrado en la transición. La población de un estado de rotación depende de dos factores. El número de moléculas en un estado excitado con número cuántico J , en relación con el número de moléculas en el estado fundamental, N _J / N ₀ viene dado por la distribución de Boltzmann como

${\displaystyle {\frac {N_{J}}{N_{0}}}=e^{-{\frac {E_{J}}{kT}}}=e^{-{\frac {BhcJ(J+1)}{kT}}}}$,

donde k es la constante de Boltzmann y T la temperatura absoluta . Este factor disminuye a medida que J aumenta. El segundo factor es la degeneración del estado rotacional, que es igual a 2J + 1. Este factor aumenta a medida que J aumenta. Combinando los dos factores ^[18]

${\displaystyle {\text{population}}\propto (2J+1)e^{-{\frac {E_{J}}{kT}}}}$

La máxima intensidad relativa se produce en ^{[19] [notas 6]}

${\displaystyle J={\sqrt {\frac {kT}{2hcB}}}-{\frac {1}{2}}}$

El diagrama de la derecha muestra un patrón de intensidad que corresponde aproximadamente al espectro que está encima de él.

Distorsión centrífuga

Cuando una molécula rota, la fuerza centrífuga separa los átomos. Como resultado, el momento de inercia de la molécula aumenta, disminuyendo así el valor de , cuando se calcula utilizando la expresión para el rotor rígido. Para tener esto en cuenta, se añade un término de corrección de distorsión centrífuga a los niveles de energía rotacional de la molécula diatómica. ^[20] ${\displaystyle B}$

${\displaystyle F\left(J\right)=BJ\left(J+1\right)-DJ^{2}\left(J+1\right)^{2}\qquad J=0,1,2,...}$

¿Dónde está la constante de distorsión centrífuga? ${\displaystyle D}$

Por lo tanto, las posiciones de línea para el modo de rotación cambian a

${\displaystyle {\tilde {\nu }}_{J^{\prime }\leftrightarrow J^{\prime \prime }}=2B\left(J^{\prime \prime }+1\right)-4D\left(J^{\prime \prime }+1\right)^{3}\qquad J^{\prime \prime }=0,1,2,...}$

En consecuencia, el espaciamiento entre líneas no es constante, como en la aproximación del rotor rígido, sino que disminuye al aumentar el número cuántico rotacional.

Una suposición subyacente a estas expresiones es que la vibración molecular sigue un movimiento armónico simple . En la aproximación armónica, la constante centrífuga se puede derivar como ${\displaystyle D}$

${\displaystyle D={\frac {h^{3}}{32\pi ^{4}I^{2}r^{2}kc}}}$

donde k es la constante de fuerza vibratoria . La relación entre y ${\displaystyle B}$ ${\displaystyle D}$

${\displaystyle D={\frac {4B^{3}}{{\tilde {\omega }}^{2}}}}$

donde es la frecuencia de vibración armónica, se deduce. Si se debe tener en cuenta la anarmonicidad, se deben agregar términos en potencias superiores de J a las expresiones para los niveles de energía y las posiciones de las líneas. ^[20] Un ejemplo sorprendente se refiere al espectro rotacional del fluoruro de hidrógeno que se ajustó a términos de hasta [J(J+1)] ⁵ . ^[21] ${\displaystyle {\tilde {\omega }}}$

Oxígeno

El momento dipolar eléctrico de la molécula de dioxígeno, O
₂es cero, pero la molécula es paramagnética con dos electrones desapareados de modo que hay transiciones magnéticas-dipolares permitidas que pueden observarse mediante espectroscopia de microondas. El espín del electrón unitario tiene tres orientaciones espaciales con respecto al vector de momento angular rotacional molecular dado, K, de modo que cada nivel rotacional se divide en tres estados, J = K + 1, K y K - 1, surgiendo cada estado J de este llamado triplete de tipo p de una orientación diferente del espín con respecto al movimiento rotacional de la molécula. La diferencia de energía entre términos J sucesivos en cualquiera de estos tripletes es de aproximadamente 2 cm ⁻¹ (60 GHz), con la única excepción de J = 1←0 diferencia que es de aproximadamente 4 cm ⁻¹ . Las reglas de selección para las transiciones dipolares magnéticas permiten transiciones entre miembros sucesivos del triplete (ΔJ = ±1) de modo que para cada valor del número cuántico de momento angular rotacional K hay dos transiciones permitidas. El núcleo ¹⁶ O tiene un momento angular de espín nuclear cero, por lo que las consideraciones de simetría exigen que K solo tenga valores impares. ^{[22] [23]}

Parte superior simétrica

En el caso de rotores simétricos, un número cuántico J está asociado con el momento angular total de la molécula. Para un valor dado de J, existe una degeneración de 2 J +1- veces con el número cuántico, M, que toma los valores + J ...0 ... - J . El tercer número cuántico, K , está asociado con la rotación sobre el eje de rotación principal de la molécula. En ausencia de un campo eléctrico externo, la energía rotacional de un trompo simétrico es una función únicamente de J y K y, en la aproximación del rotor rígido, la energía de cada estado rotacional está dada por

${\displaystyle F\left(J,K\right)=BJ\left(J+1\right)+\left(A-B\right)K^{2}\qquad J=0,1,2,\ldots \quad {\mbox{and}}\quad K=+J,\ldots ,0,\ldots ,-J}$

donde y para una molécula superior simétrica alargada o para una molécula achatada . ${\displaystyle B={h \over {8\pi ^{2}cI_{B}}}}$ ${\displaystyle A={h \over {8\pi ^{2}cI_{A}}}}$ ${\displaystyle A={h \over {8\pi ^{2}cI_{C}}}}$

Esto da como resultado los números de onda de transición como

${\displaystyle {\tilde {\nu }}_{J^{\prime }\leftrightarrow J^{\prime \prime },K}=F\left(J^{\prime },K\right)-F\left(J^{\prime \prime },K\right)=2B\left(J^{\prime \prime }+1\right)\qquad J^{\prime \prime }=0,1,2,...}$

que es lo mismo que en el caso de una molécula lineal. ^[24] Con una corrección de primer orden por distorsión centrífuga, los números de onda de transición se convierten en

${\displaystyle {\tilde {\nu }}_{J^{\prime }\leftrightarrow J^{\prime \prime },K}=F\left(J^{\prime },K\right)-F\left(J^{\prime \prime },K\right)=2\left(B-2D_{JK}K^{2}\right)\left(J^{\prime \prime }+1\right)-4D_{J}\left(J^{\prime \prime }+1\right)^{3}\qquad J^{\prime \prime }=0,1,2,...}$

El término en D _JK tiene el efecto de eliminar la degeneración presente en la aproximación del rotor rígido, con diferentes valores de K. ^[25]

Top asimétrico

Espectro de rotación puro del vapor de agua atmosférico medido en Mauna Kea (33 cm ⁻¹ a 100 cm ⁻¹ )

El número cuántico J se refiere al momento angular total, como antes. Puesto que hay tres momentos de inercia independientes, hay otros dos números cuánticos independientes a considerar, pero los valores de los términos para un rotor asimétrico no se pueden derivar en forma cerrada. Se obtienen por diagonalización de matrices individuales para cada valor J. Hay fórmulas disponibles para moléculas cuya forma se aproxima a la de un trompo simétrico. ^[26]

La molécula de agua es un ejemplo importante de un trompo asimétrico. Tiene un espectro de rotación puro e intenso en la región del infrarrojo lejano, por debajo de unos 200 cm ⁻¹ . Por este motivo, los espectrómetros de infrarrojo lejano deben liberarse del vapor de agua atmosférico, ya sea mediante purga con un gas seco o mediante evacuación. El espectro se ha analizado en detalle. ^[27]

División cuadripolar

Cuando un núcleo tiene un número cuántico de espín , I , mayor que 1/2, tiene un momento cuadrupolar . En ese caso, el acoplamiento del momento angular de espín nuclear con el momento angular rotacional causa la división de los niveles de energía rotacional. Si el número cuántico J de un nivel rotacional es mayor que I , se producen 2 niveles I + 1 ; pero si J es menor que I , resultan 2 niveles J + 1. El efecto es un tipo de división hiperfina . Por ejemplo, con ¹⁴ N ( I = 1 ) en HCN, todos los niveles con J > 0 se dividen en 3. Las energías de los subniveles son proporcionales al momento cuadrupolar nuclear y una función de F y J. donde F = J + I , J + I − 1, …, | J − I | . Por lo tanto, la observación de la división cuadrupolar nuclear permite determinar la magnitud del momento cuadrupolar nuclear. ^[28] Este es un método alternativo al uso de la espectroscopia de resonancia cuadrupolo nuclear . La regla de selección para las transiciones rotacionales se convierte en ^[29]

${\displaystyle \Delta J=\pm 1,\Delta F=0,\pm 1}$

Efectos Stark y Zeeman

En presencia de un campo eléctrico externo estático, la degeneración 2 J + 1 de cada estado rotacional se elimina parcialmente, un ejemplo de un efecto Stark . Por ejemplo, en moléculas lineales, cada nivel de energía se divide en componentes J + 1. El grado de división depende del cuadrado de la intensidad del campo eléctrico y del cuadrado del momento dipolar de la molécula. ^[30] En principio, esto proporciona un medio para determinar el valor del momento dipolar molecular con alta precisión. Los ejemplos incluyen sulfuro de carbonilo , OCS, con μ = 0,71521 ± 0,00020 debye . Sin embargo, debido a que la división depende de μ ² , la orientación del dipolo debe deducirse a partir de consideraciones mecánicas cuánticas. ^[31]

Una eliminación similar de la degeneración ocurrirá cuando una molécula paramagnética se coloque en un campo magnético, un ejemplo del efecto Zeeman . La mayoría de las especies que se pueden observar en estado gaseoso son diamagnéticas . Las excepciones son las moléculas con electrones impares, como el óxido nítrico , NO, el dióxido de nitrógeno , NO
₂, algunos óxidos de cloro y el radical hidroxilo . El efecto Zeeman se ha observado con dioxígeno , O
₂^[32]

Espectroscopia Raman rotacional

Las transiciones rotacionales moleculares también se pueden observar mediante espectroscopia Raman . Las transiciones rotacionales están permitidas por Raman para cualquier molécula con una polarizabilidad anisotrópica que incluye todas las moléculas excepto las cimas esféricas. Esto significa que las transiciones rotacionales de moléculas sin momento dipolar permanente, que no se pueden observar en la absorción o emisión, se pueden observar, por dispersión, en la espectroscopia Raman. Se pueden obtener espectros Raman de muy alta resolución adaptando un espectrómetro infrarrojo por transformada de Fourier . Un ejemplo es el espectro de¹⁵
norte
₂Se muestra el efecto del espín nuclear, que da como resultado una variación de intensidad de 3:1 en las líneas adyacentes. A partir de los datos se dedujo una longitud de enlace de 109,9985 ± 0,0010 pm. ^[33]

Instrumentos y métodos

La gran mayoría de los espectrómetros actuales utilizan una combinación de componentes disponibles comercialmente y personalizados que los usuarios integran según sus necesidades particulares. Los instrumentos se pueden clasificar en general según sus principios operativos generales. Aunque se pueden encontrar transiciones rotacionales en una región muy amplia del espectro electromagnético , existen limitaciones físicas fundamentales en el ancho de banda operativo de los componentes del instrumento. A menudo resulta poco práctico y costoso cambiar a mediciones dentro de una región de frecuencia completamente diferente. Los instrumentos y principios operativos que se describen a continuación son generalmente apropiados para experimentos de espectroscopia de microondas realizados a frecuencias entre 6 y 24 GHz.

Células de absorción y modulación de Stark

Un espectrómetro de microondas se puede construir de forma más sencilla utilizando una fuente de radiación de microondas, una celda de absorción en la que se puede introducir un gas de muestra y un detector como un receptor superheterodino . Se puede obtener un espectro barriendo la frecuencia de la fuente mientras se detecta la intensidad de la radiación transmitida. Una sección simple de guía de ondas puede servir como celda de absorción. Una variación importante de la técnica en la que se aplica una corriente alterna a través de electrodos dentro de la celda de absorción da como resultado una modulación de las frecuencias de las transiciones rotacionales. Esto se conoce como modulación Stark y permite el uso de métodos de detección sensibles a la fase que ofrecen una sensibilidad mejorada. La espectroscopia de absorción permite el estudio de muestras que son termodinámicamente estables a temperatura ambiente. El primer estudio del espectro de microondas de una molécula ( NH
₃) fue realizado por Cleeton & Williams en 1934. ^[34] Experimentos posteriores explotaron fuentes potentes de microondas como el klistrón , muchas de las cuales fueron desarrolladas para radar durante la Segunda Guerra Mundial . El número de experimentos en espectroscopia de microondas aumentó inmediatamente después de la guerra. Para 1948, Walter Gordy pudo preparar una revisión de los resultados contenidos en aproximadamente 100 artículos de investigación. ^[35] Las versiones comerciales ^[36] del espectrómetro de absorción de microondas fueron desarrolladas por Hewlett-Packard en la década de 1970 y alguna vez fueron ampliamente utilizadas para la investigación fundamental. La mayoría de los laboratorios de investigación ahora explotan espectrómetros de microondas de transformada de Fourier de pulso chirriante (FTMW) o Balle- Flygare .

Espectroscopia de microondas por transformada de Fourier (FTMW)

El marco teórico ^[37] que sustenta la espectroscopia FTMW es análogo al utilizado para describir la espectroscopia FT-NMR . El comportamiento del sistema en evolución se describe mediante ecuaciones ópticas de Bloch . Primero, se introduce un pulso de microondas corto (normalmente de 0 a 3 microsegundos de duración) en resonancia con una transición rotacional. Las moléculas que absorben la energía de este pulso son inducidas a rotar coherentemente en fase con la radiación incidente. La desactivación del pulso de polarización es seguida por la emisión de microondas que acompaña la decoherencia del conjunto molecular. Esta desintegración por inducción libre ocurre en una escala de tiempo de 1 a 100 microsegundos dependiendo de la configuración del instrumento. Tras el trabajo pionero de Dicke y sus colaboradores en la década de 1950, ^{[38] Ekkers y} Flygare construyeron el primer espectrómetro FTMW en 1975. ^[39]

Espectrómetro Balle-Flygare FTMW

Balle, Campbell, Keenan y Flygare demostraron que la técnica FTMW se puede aplicar dentro de una "celda de espacio libre" que comprende una cámara evacuada que contiene una cavidad Fabry-Perot . ^[40] Esta técnica permite que una muestra sea sondeada solo milisegundos después de que se somete a un enfriamiento rápido a solo unos pocos kelvins en la garganta de un chorro de gas en expansión. Este fue un desarrollo revolucionario porque (i) enfriar las moléculas a bajas temperaturas concentra la población disponible en los niveles de energía rotacional más bajos. Junto con los beneficios conferidos por el uso de una cavidad Fabry-Perot, esto trajo consigo una gran mejora en la sensibilidad y resolución de los espectrómetros junto con una reducción en la complejidad de los espectros observados; (ii) se hizo posible aislar y estudiar moléculas que están muy débilmente unidas porque no hay suficiente energía disponible para que experimenten fragmentación o reacción química a temperaturas tan bajas. William Klemperer fue un pionero en el uso de este instrumento para la exploración de interacciones débilmente unidas. Si bien la cavidad Fabry-Perot de un espectrómetro FTMW Balle-Flygare puede ajustarse normalmente en resonancia a cualquier frecuencia entre 6 y 18 GHz, el ancho de banda de las mediciones individuales está restringido a aproximadamente 1 MHz. Una animación ilustra el funcionamiento de este instrumento, que actualmente es la herramienta más utilizada para la espectroscopia de microondas. ^[41]

Espectrómetro FTMW de pulso chirriante

Al observar que los digitalizadores y la tecnología electrónica relacionada habían progresado significativamente desde el inicio de la espectroscopia FTMW, BH Pate de la Universidad de Virginia ^[42] diseñó un espectrómetro ^[43] que conserva muchas ventajas del espectrómetro FT-MW de Balle-Flygare, al tiempo que innova en (i) el uso de un generador de formas de onda arbitrarias de alta velocidad (>4 GS/s) para generar un pulso de polarización de microondas "chirriante" que barre hasta 12 GHz de frecuencia en menos de un microsegundo y (ii) el uso de un osciloscopio de alta velocidad (>40 GS/s) para digitalizar y transformar Fourier la desintegración por inducción libre molecular. El resultado es un instrumento que permite el estudio de moléculas débilmente unidas pero que es capaz de explotar un ancho de banda de medición (12 GHz) que es mucho mayor en comparación con el espectrómetro FTMW de Balle-Flygare. Varios grupos en Estados Unidos, Canadá y Europa han construido versiones modificadas del espectrómetro CP-FTMW original. ^{[44] [45]} El instrumento ofrece una capacidad de banda ancha que complementa en gran medida la alta sensibilidad y resolución que ofrece el diseño de Balle-Flygare.

Notas

1. El espectro se midió durante un par de horas con la ayuda de un espectrómetro de microondas con transformada de Fourier de pulso chirriante en la Universidad de Bristol.
2. Este artículo utiliza la convención de los espectroscopistas moleculares para expresar la constante rotacional en cm ⁻¹ . Por lo tanto, en este artículo se corresponde con el artículo sobre rotores rígidos. ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle {\bar {B}}=B/hc}$
3. En el caso de un trompo simétrico, los valores de los dos momentos de inercia se pueden utilizar para derivar dos parámetros moleculares. Los valores de cada isotopólogo adicional proporcionan la información de un parámetro molecular más. En el caso de trompos asimétricos, un único isotopólogo proporciona información para un máximo de tres parámetros moleculares.
4. Estas transiciones se denominan transiciones permitidas por dipolos eléctricos. También se pueden permitir otras transiciones que involucran cuadrupolos, octupolos, hexadecápolos, etc., pero la intensidad espectral es mucho menor, por lo que estas transiciones son difíciles de observar. Las transiciones permitidas por dipolos magnéticos pueden ocurrir en moléculas paramagnéticas como el dioxígeno , O
   ₂y óxido nítrico , NO
5. En la espectroscopia Raman, las energías de los fotones para la dispersión de Stokes y anti-Stokes son, respectivamente, menores y mayores que la energía del fotón incidente. Véase el diagrama de niveles de energía en Espectroscopia Raman .
6. Este valor de J corresponde al máximo de la población considerada como función continua de J. Sin embargo, como solo se permiten valores enteros de J, la intensidad máxima de la línea se observa para un entero vecino J.

Referencias

1. Gordy, W. (1970). A. Weissberger (ed.). Espectros moleculares de microondas en la técnica de la química orgánica . Vol. IX. Nueva York: Interscience.
2. Nair, KPR; Demaison, J.; Wlodarczak, G.; Merke, I. (236). "Espectro rotacional de ondas milimétricas y rotación interna en o-clorotolueno". Journal of Molecular Spectroscopy . 237 (2): 137–142. Bibcode :2006JMoSp.237..137N. doi :10.1016/j.jms.2006.03.011.
3. Cheung, AC; Rank, DM; Townes, CH; Thornton, DD y Welch, WJ (1968). "Detección de NH
   ₃Moléculas en el medio interestelar por sus espectros de emisión de microondas". Physical Review Letters . 21 (25): 1701–5. Bibcode :1968PhRvL..21.1701C. doi :10.1103/PhysRevLett.21.1701.
4. Ricaud, P.; Baron, P; de La Noë, J. (2004). "Evaluación de la calidad de las mediciones terrestres por microondas de monóxido de cloro, ozono y dióxido de nitrógeno del radiómetro NDSC en el Plateau de Bure". Ann. Geophys . 22 (6): 1903–15. Bibcode :2004AnGeo..22.1903R. doi : 10.5194/angeo-22-1903-2004 .
5. "Astroquímica en Virginia" . Consultado el 2 de diciembre de 2012 .
6. Atkins y de Paula 2006, pág. 444
7. Banwell y McCash 1994, pág. 99
8. Valores del momento de inercia de Atkins y de Paula 2006, p. 445
9. Hollas 1996, pág. 95
10. Hollas 1996, p. 104 muestra parte del espectro rotacional observado del silano.
11. Atkins y de Paula 2006, pág. 447
12. Banwell y McCash 1994, pág. 49
13. Hollas 1996, pág. 111
14. Atkins y de Paula 2006, págs. 474–5
15. Banwell & McCash 1994, Sección 4.2, pág. 105, Espectros Raman rotacionales puros
16. Alexander, AJ; Kroto, HW; Walton, DRM (1967). "El espectro de microondas, la estructura de sustitución y el momento dipolar de la cianobutadiina". J. Mol. Spectrosc . 62 (2): 175–180. Código Bibliográfico :1976JMoSp..62..175A. doi :10.1016/0022-2852(76)90347-7.Ilustrado en Hollas 1996, p. 97
17. Banwell y McCash 1994, pág. 63.
18. Banwell y McCash 1994, pág. 40
19. Atkins y de Paula 2006, pág. 449
20. Banwell y McCash 1994, pág. 45
21. Jennings, DA; Evenson, KM; Zink, LR; Demuynck, C.; Destombes, JL; Lemoine, B; Johns, JWC (abril de 1987). "Espectroscopia de alta resolución de HF de 40 a 1100 cm ⁻¹ : Constantes rotacionales de alta precisión". Journal of Molecular Spectroscopy . 122 (2): 477–480. Código Bibliográfico :1987JMoSp.122..477J. doi :10.1016/0022-2852(87)90021-X.pdf
22. Strandberg, MWP; Meng, CY; Ingersoll, JG (1949). "El espectro de absorción de microondas del oxígeno". Phys. Rev . 75 (10): 1524–8. Código Bibliográfico :1949PhRv...75.1524S. doi :10.1103/PhysRev.75.1524.pdf
23. Krupenie, Paul H. (1972). "El espectro del oxígeno molecular" (PDF) . Journal of Physical and Chemical Reference Data . 1 (2): 423–534. Bibcode :1972JPCRD...1..423K. doi :10.1063/1.3253101.
24. Hollas 1996, pág. 101
25. Hollas 1996, p. 102 muestra el efecto sobre el espectro de microondas de H
    ₃SiNCS .
26. Hollas 1996, pág. 103
27. Hall, Richard T.; Dowling, Jerome M. (1967). "Espectro rotacional puro del vapor de agua". J. Chem. Phys . 47 (7): 2454–61. Código Bibliográfico :1967JChPh..47.2454H. doi :10.1063/1.1703330.Hall, Richard T.; Dowling, Jerome M. (1971). "Fe de erratas: espectro rotacional puro del vapor de agua". J. Chem. Phys . 54 (11): 4968. Código Bibliográfico :1971JChPh..54.4968H. doi : 10.1063/1.1674785 .
28. Simmons, James W.; Anderson, Wallace E.; Gordy, Walter (1950). "Espectro de microondas y constantes moleculares del cianuro de hidrógeno". Phys. Rev . 77 (1): 77–79. Bibcode :1950PhRv...77...77S. doi :10.1103/PhysRev.77.77.
29. Chang, Raymond (1971). Principios básicos de espectroscopia . McGraw-Hill.pág. 139
30. Hollas 1996, p. 102 da las ecuaciones para moléculas diatómicas y tops simétricos
31. Hollas 1996, pág. 102
32. Burkhalter, James H.; Roy S. Anderson; William V. Smith; Walter Gordy (1950). "La estructura fina del espectro de absorción de microondas del oxígeno". Phys. Rev . 79 (4): 651–5. Bibcode :1950PhRv...79..651B. doi :10.1103/PhysRev.79.651.
33. Hollas 1996, p. 113, ilustra el espectro de¹⁵
    norte
    ₂obtenido utilizando radiación de 476,5 nm de un láser de iones de argón .
34. Cleeton, CE; Williams, NH (1934). "Ondas electromagnéticas de 1,1 cm de longitud de onda y espectro de absorción del amoníaco". Physical Review . 45 (4): 234–7. Bibcode :1934PhRv...45..234C. doi :10.1103/PhysRev.45.234.
35. Gordy, W. (1948). "Espectroscopia de microondas". Reseñas de Física Moderna . 20 (4): 668–717. Bibcode :1948RvMP...20..668G. doi :10.1103/RevModPhys.20.668.
36. "Junio ​​de 1971, Revista Hewlett-Packard" (PDF) .
37. Schwendemann, RH (1978). "Efectos transitorios en espectroscopia de microondas". Annu. Rev. Phys. Chem . 29 : 537–558. Código Bibliográfico :1978ARPC...29..537S. doi :10.1146/annurev.pc.29.100178.002541.
38. Dicke, RH; Romer, RH (1955). "Técnicas de pulso en espectroscopia de microondas". Rev. Sci. Instrum . 26 (10): 915–928. Bibcode :1955RScI...26..915D. doi :10.1063/1.1715156.
39. Ekkers, J.; Flygare, WH (1976). "Espectrómetro de transformada de Fourier de microondas pulsada". Rev. Sci. Instrum . 47 (4): 448–454. Bibcode :1976RScI...47..448E. doi :10.1063/1.1134647.
40. Balle, TJ; Campbell, EJ; Keenan, MR; Flygare, WH (1980). "Un nuevo método para observar los espectros rotacionales de complejos moleculares débiles: KrHCl". J. Chem. Phys . 72 (2): 922–932. Bibcode :1980JChPh..72..922B. doi :10.1063/1.439210.
41. Jager, W. "Animación del espectrómetro Balle-Flygare FTMW".
42. "Página web del Grupo de Investigación BH Pate, Departamento de Química, Universidad de Virginia".
43. Brown, GG; Dian, BC; Douglass, KO; Geyer, SM; Pate, BH (2006). "El espectro rotacional de la epifluorohidrina medido por espectroscopia de microondas con transformada de Fourier de pulso chirriante". J. Mol. Spectrosc . 238 (2): 200–212. Bibcode :2006JMoSp.238..200B. doi :10.1016/j.jms.2006.05.003.
44. Grubbs, GS; Dewberry, CT; Etchison, KC; Kerr, KE; Cooke, SA (2007). "Un espectrómetro de microondas de transformada de Fourier de intensidad correcta acelerada por búsqueda con fuente de ablación láser pulsada". Rev. Sci. Instrum . 78 (9): 096106–096106–3. Bibcode :2007RScI...78i6106G. doi :10.1063/1.2786022. PMID  17902981.
45. Wilcox, DS; Hotopp, KM; Dian, BC (2011). "Espectroscopia de microondas por transformada de Fourier de pulso chirriante bidimensional". J. Phys. Chem. A . 115 (32): 8895–8905. Bibcode :2011JPCA..115.8895W. doi :10.1021/jp2043202. PMID  21728367.

Bibliografía

• Atkins, PW ; de Paula, J. (2006). "Espectroscopia molecular: Sección: Espectros de rotación pura". Química física (8.ª ed.). Oxford University Press. págs. 431–469. ISBN 0198700725.
• Banwell, Colin N.; McCash, Elaine M. (1994). Fundamentos de espectroscopia molecular (4.ª ed.). McGraw-Hill. ISBN 0-07-707976-0.
• Brown, John M.; Carrington, Alan (2003). Espectroscopia rotacional de moléculas diatómicas. Cambridge University Press. ISBN 0-521-53078-4.
• Hollas, MJ (1996). Espectroscopia moderna (3.ª ed.). Wiley. ISBN 0471965227.
• Kroto, HW (2003). Espectroscopia de rotación molecular . Dover. ISBN 0-486-49540-X.
• McQuarrie, Donald A. (2008). Química cuántica. Libros de ciencia de la universidad. ISBN 978-1-891389-50-4.
• Townes, Charles H. ; Schawlow, Arthur L. (1975). Espectroscopia de microondas. Dover. ISBN 978-0-486-61798-5.
• Kovács, István (1969). Estructura rotacional en los espectros de moléculas diatómicas . Adam Hilger. ISBN 0852741421.
• Wollrab, James E. (1967). Espectros rotacionales y estructura molecular. Academic Press. ISBN 148319485X.

Enlaces externos

• Simulador de espectros de gases infrarrojos
• Artículo de Hyperphysics sobre el espectro rotacional
• Lista de grupos de investigación en espectroscopia de microondas en todo el mundo