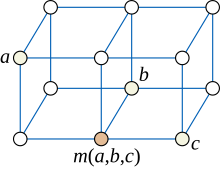
En teoría de grafos , una división de las matemáticas , un grafo mediano es un grafo no dirigido en el que cada tres vértices a , b y c tienen una mediana única : un vértice m ( a , b , c ) que pertenece a los caminos más cortos entre cada par de a , b y c .
El concepto de grafos medianos ha sido estudiado durante mucho tiempo, por ejemplo por Birkhoff y Kiss (1947) o (más explícitamente) por Avann (1961), pero el primer artículo en llamarlos "grafos medianos" parece ser Nebeský (1971). Como escriben Chung , Graham y Saks, "los grafos medianos surgen naturalmente en el estudio de conjuntos ordenados y redes distributivas discretas , y tienen una extensa literatura". [1] En filogenética , el grafo de Buneman que representa todos los árboles evolutivos de máxima parsimonia es un grafo mediano. [2] Los grafos medianos también surgen en la teoría de la elección social : si un conjunto de alternativas tiene la estructura de un grafo mediano, es posible derivar de manera inequívoca una preferencia mayoritaria entre ellas. [3]
Klavžar y Mulder (1999), Bandelt y Chepoi (2008) y Knuth (2008) ofrecen estudios adicionales de gráficos medianos.
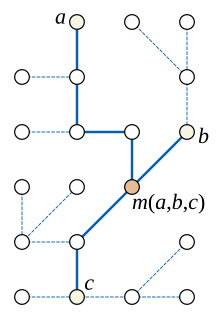
Todo árbol es un grafo mediano. Para comprobarlo, observe que en un árbol, la unión de los tres caminos más cortos entre pares de los tres vértices a , b y c es en sí misma un camino o un subárbol formado por tres caminos que se encuentran en un único nodo central de grado tres. Si la unión de los tres caminos es en sí misma un camino, la mediana m ( a , b , c ) es igual a uno de a , b o c , cualquiera de estos tres vértices que esté entre los otros dos en el camino. Si el subárbol formado por la unión de los tres caminos no es un camino, la mediana de los tres vértices es el nodo central de grado tres del subárbol. [4]
Los gráficos de cuadrícula proporcionan ejemplos adicionales de gráficos de mediana . En un gráfico de cuadrícula, las coordenadas de la mediana m ( a , b , c ) se pueden encontrar como la mediana de las coordenadas de a , b y c . Por el contrario, resulta que, en cada gráfico de mediana, uno puede etiquetar los vértices por puntos en una red de números enteros de tal manera que las medianas se pueden calcular por coordenadas de esta manera. [5]
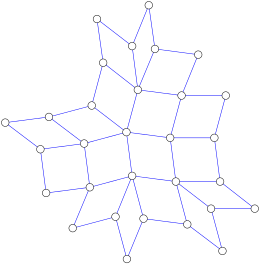
Los grafos cuadrados , grafos planares en los que todas las caras interiores son cuadriláteros y todos los vértices interiores tienen cuatro o más aristas incidentes, son otra subclase de los grafos medianos. [6] Un poliominó es un caso especial de un grafo cuadrado y por lo tanto también forma un grafo mediano. [7]
El grafo simplex κ( G ) de un grafo arbitrario no dirigido G tiene un vértice para cada camarilla (subgrafo completo) de G ; dos vértices de κ( G ) están unidos por una arista si las camarillas correspondientes difieren en un vértice de G . El grafo simplex es siempre un grafo mediano, en el que la mediana de un triple dado de camarillas se puede formar utilizando la regla de la mayoría para determinar qué vértices de las camarillas incluir. [8]
Ningún gráfico de ciclo de longitud distinta de cuatro puede ser un gráfico de mediana. Cada uno de estos ciclos tiene tres vértices a , b y c, de modo que los tres caminos más cortos rodean por completo el ciclo sin tener una intersección común. Para un triple de vértices de este tipo, no puede haber mediana.
En un grafo arbitrario, para cada dos vértices a y b , el número mínimo de aristas entre ellos se denomina distancia , denotada por d ( x , y ). El intervalo de vértices que se encuentran en caminos más cortos entre a y b se define como
Un gráfico mediano se define por la propiedad de que, por cada tres vértices a , b y c , estos intervalos se intersecan en un solo punto:
De manera equivalente, para cada tres vértices a , b y c se puede encontrar un vértice m ( a , b , c ) tal que las distancias no ponderadas en el gráfico satisfagan las igualdades
y m ( a , b , c ) es el único vértice para el cual esto es cierto.
También es posible definir gráficos medianos como los conjuntos de soluciones de problemas de 2-satisfacibilidad , como las retracciones de hipercubos , como los gráficos de álgebras medianas finitas , como los gráficos de Buneman de sistemas divididos de Helly y como los gráficos de windex 2; consulte las secciones siguientes.

En la teoría de redes , el grafo de una red finita tiene un vértice para cada elemento de la red y una arista para cada par de elementos en la relación de recubrimiento de la red. Las redes se presentan visualmente comúnmente a través de diagramas de Hasse , que son dibujos de grafos de redes. Estos grafos, especialmente en el caso de redes distributivas , resultan estar estrechamente relacionados con los grafos medianos.
En una red distributiva, la operación mediana ternaria autodual de Birkhoff [9]
satisface ciertos axiomas clave, que comparte con la mediana habitual de números en el rango de 0 a 1 y con las álgebras medianas en general:
La ley distributiva puede ser sustituida por una ley asociativa: [10]
La operación mediana también puede utilizarse para definir una noción de intervalos para redes distributivas:
El grafo de una red distributiva finita tiene una arista entre los vértices a y b siempre que I ( a , b ) = { a , b }. Para cada dos vértices a y b de este grafo, el intervalo I ( a , b ) definido en términos de teoría de la red anteriormente consiste en los vértices en caminos más cortos de a a b , y por lo tanto coincide con los intervalos de teoría de grafos definidos anteriormente. Para cada tres elementos de la red a , b y c , m ( a , b , c ) es la única intersección de los tres intervalos I ( a , b ), I ( a , c ) e I ( b , c ) . [12] Por lo tanto, el grafo de una red distributiva finita arbitraria es un grafo mediano. Por el contrario, si un grafo mediano G contiene dos vértices 0 y 1 tales que cada otro vértice se encuentra en un camino más corto entre los dos (equivalentemente, m (0, a ,1) = a para todo a ), entonces podemos definir una red distributiva en la que a ∧ b = m ( a ,0, b ) y a ∨ b = m ( a ,1, b ), y G será el grafo de esta red. [13]
Duffus y Rival (1983) caracterizan los grafos de redes distributivas directamente como retractos de hipercubos que preservan el diámetro. En términos más generales, cada grafo mediano da lugar a una operación ternaria m que satisface la idempotencia, la conmutatividad y la distributividad, pero posiblemente sin los elementos de identidad de una red distributiva. Toda operación ternaria sobre un conjunto finito que satisface estas tres propiedades (pero que no necesariamente tiene elementos 0 y 1) da lugar de la misma manera a un grafo mediano. [14]
En un grafo mediano, se dice que un conjunto S de vértices es convexo si, por cada dos vértices a y b pertenecientes a S , todo el intervalo I ( a , b ) es un subconjunto de S . De manera equivalente, dadas las dos definiciones de intervalos anteriores, S es convexo si contiene cada camino más corto entre dos de sus vértices, o si contiene la mediana de cada conjunto de tres puntos al menos dos de los cuales son de S . Obsérvese que la intersección de cada par de conjuntos convexos es en sí misma convexa. [15]
Los conjuntos convexos en un grafo mediano tienen la propiedad de Helly : si F es una familia arbitraria de conjuntos convexos que se intersecan por pares, entonces todos los conjuntos en F tienen una intersección común. [16] Porque, si F tiene sólo tres conjuntos convexos S , T y U en él, con a en la intersección del par S y T , b en la intersección del par T y U , y c en la intersección del par S y U , entonces cada camino más corto de a a b debe estar dentro de T por convexidad, y de manera similar cada camino más corto entre los otros dos pares de vértices debe estar dentro de los otros dos conjuntos; pero m ( a , b , c ) pertenece a caminos entre los tres pares de vértices, por lo que se encuentra dentro de los tres conjuntos y forma parte de su intersección común. Si F tiene más de tres conjuntos convexos, el resultado se sigue por inducción sobre el número de conjuntos, ya que uno puede reemplazar un par arbitrario de conjuntos en F por su intersección, usando el resultado para triples de conjuntos para mostrar que la familia reemplazada todavía se interseca por pares.
Una familia particularmente importante de conjuntos convexos en un gráfico mediano, que desempeñan un papel similar al de los semiespacios en el espacio euclidiano, son los conjuntos
definido para cada arista uv del grafo. En palabras, W uv consiste en los vértices más cercanos a u que a v , o equivalentemente los vértices w tales que algún camino más corto de v a w pasa por u . Para mostrar que W uv es convexo, sea w 1 w 2 ... w k un camino más corto arbitrario que comienza y termina dentro de W uv ; entonces w 2 también debe estar dentro de W uv , porque de lo contrario los dos puntos m 1 = m ( u , w 1 , w k ) y m 2 = m ( m 1 , w 2 ... w k ) podrían demostrarse (considerando las posibles distancias entre los vértices) como medianas distintas de u , w 1 y w k , contradiciendo la definición de un grafo mediano que requiere que las medianas sean únicas. Por lo tanto, cada vértice sucesivo en un camino más corto entre dos vértices de W uv también se encuentra dentro de W uv , por lo que W uv contiene todos los caminos más cortos entre sus nodos, una de las definiciones de convexidad.
La propiedad de Helly para los conjuntos W uv juega un papel clave en la caracterización de los gráficos medianos como la solución de las instancias de 2-satisfacibilidad, a continuación.
Los gráficos medianos tienen una conexión estrecha con los conjuntos de soluciones de problemas de 2-satisfacibilidad que pueden usarse tanto para caracterizar estos gráficos como para relacionarlos con mapas de hipercubos que preservan la adyacencia. [17]
Una instancia de 2-satisfacibilidad consiste en una colección de variables booleanas y una colección de cláusulas , restricciones sobre ciertos pares de variables que requieren que esas dos variables eviten ciertas combinaciones de valores. Por lo general, estos problemas se expresan en forma normal conjuntiva , en la que cada cláusula se expresa como una disyunción y todo el conjunto de restricciones se expresa como una conjunción de cláusulas, como
Una solución para tal caso es una asignación de valores de verdad a las variables que satisface todas las cláusulas, o equivalentemente, que hace que la expresión en forma normal conjuntiva para el caso se vuelva verdadera cuando se sustituyen los valores de las variables en ella. La familia de todas las soluciones tiene una estructura natural como un álgebra de medianas, donde la mediana de tres soluciones se forma eligiendo cada valor de verdad como la función mayoritaria de los valores en las tres soluciones; es sencillo verificar que esta solución mediana no puede violar ninguna de las cláusulas. Por lo tanto, estas soluciones forman un grafo de medianas, en el que el vecino de cada solución se forma negando un conjunto de variables que están todas restringidas a ser iguales o desiguales entre sí.
Por el contrario, cada grafo mediano G puede representarse de esta manera como el conjunto solución de una instancia de 2-satisfacibilidad. Para encontrar dicha representación, cree una instancia de 2-satisfacibilidad en la que cada variable describa la orientación de una de las aristas del grafo (una asignación de una dirección a la arista que hace que el grafo se vuelva dirigido en lugar de no dirigido) y cada restricción permita que dos aristas compartan un par de orientaciones solo cuando existe un vértice v tal que ambas orientaciones se encuentran a lo largo de caminos más cortos desde otros vértices hasta v . Cada vértice v de G corresponde a una solución de esta instancia de 2-satisfacibilidad en la que todas las aristas están dirigidas hacia v . Cada solución de la instancia debe provenir de algún vértice v de esta manera, donde v es la intersección común de los conjuntos W uw para las aristas dirigidas desde w a u ; esta intersección común existe debido a la propiedad de Helly de los conjuntos W uw . Por lo tanto, las soluciones de esta instancia de 2-satisfacibilidad se corresponden uno a uno con los vértices de G .
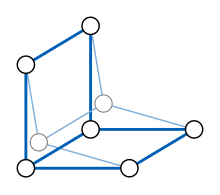
Una retracción de un grafo G es una función que preserva la adyacencia de G a uno de sus subgrafos. [18] Más precisamente, es el homomorfismo de grafos φ de G a sí mismo tal que φ( v ) = v para cada vértice v en el subgrafo φ(G). La imagen de la retracción se llama retracción de G . Las retracciones son ejemplos de funciones métricas : la distancia entre φ( v ) y φ( w ), para cada v y w , es como máximo igual a la distancia entre v y w , y es igual siempre que v y w pertenezcan a φ( G ). Por lo tanto, una retracción debe ser un subgrafo isométrico de G : las distancias en la retracción son iguales a las de G .
Si G es un grafo mediano, y a , b y c son tres vértices arbitrarios de una retracción φ( G ), entonces φ( m ( a , b , c )) debe ser una mediana de a , b y c , y por lo tanto debe ser igual a m ( a , b , c ). Por lo tanto, φ( G ) contiene las medianas de todos los triples de sus vértices, y también debe ser un grafo mediano. En otras palabras, la familia de grafos medianos está cerrada bajo la operación de retracción. [19]
Un grafo de hipercubo , en el que los vértices corresponden a todos los posibles vectores de bits de k bits y en el que dos vértices son adyacentes cuando los vectores de bits correspondientes difieren en un solo bit, es un caso especial de un grafo de cuadrícula de dimensión k y, por lo tanto, es un grafo de mediana. La mediana de tres vectores de bits a , b y c se puede calcular calculando, en cada posición de bit, la función mayoritaria de los bits de a , b y c . Dado que los grafos de mediana están cerrados bajo retracción e incluyen los hipercubos, cada retracción de un hipercubo es un grafo de mediana.
Por el contrario, todo grafo mediano debe ser la retracción de un hipercubo. [20] Esto puede verse a partir de la conexión, descrita anteriormente, entre grafos medianos y 2-satisfacibilidad: sea G el grafo de soluciones para una instancia de 2-satisfacibilidad; sin pérdida de generalidad, esta instancia puede formularse de tal manera que no haya dos variables que sean siempre iguales o siempre desiguales en cada solución. Entonces, el espacio de todas las asignaciones de verdad a las variables de esta instancia forma un hipercubo. Para cada cláusula, formada como la disyunción de dos variables o sus complementos, en la instancia de 2-satisfacibilidad, se puede formar una retracción del hipercubo en la que las asignaciones de verdad que violan esta cláusula se mapean a asignaciones de verdad en las que ambas variables satisfacen la cláusula, sin cambiar las otras variables en la asignación de verdad. La composición de las retracciones formadas de esta manera para cada una de las cláusulas da una retracción del hipercubo sobre el espacio de solución de la instancia y, por lo tanto, da una representación de G como la retracción de un hipercubo. En particular, los grafos medianos son subgrafos isométricos de hipercubos y, por lo tanto, son cubos parciales . Sin embargo, no todos los cubos parciales son grafos medianos; por ejemplo, un grafo de ciclo de seis vértices es un cubo parcial pero no es un grafo mediano.
Como describen Imrich y Klavžar (2000), una incrustación isométrica de un gráfico mediano en un hipercubo se puede construir en tiempo O( m log n ), donde n y m son los números de vértices y aristas del gráfico respectivamente. [21]
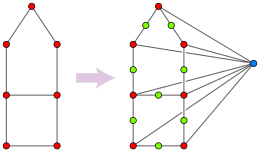
Los problemas de probar si un gráfico es un gráfico mediano y si un gráfico está libre de triángulos , ambos habían sido bien estudiados cuando Imrich, Klavžar y Mulder (1999) observaron que, en cierto sentido, son computacionalmente equivalentes. [22] Por lo tanto, el límite de tiempo mejor conocido para probar si un gráfico está libre de triángulos, O( m 1.41 ), [23] se aplica también para probar si un gráfico es un gráfico mediano, y cualquier mejora en los algoritmos de prueba de gráficos medianos también conduciría a una mejora en los algoritmos para detectar triángulos en gráficos.
En una dirección, supongamos que se nos da como entrada un grafo G , y debemos comprobar si G no tiene triángulos. A partir de G , construyamos un nuevo grafo H que tenga como vértices cada conjunto de cero, uno o dos vértices adyacentes de G . Dos de estos conjuntos son adyacentes en H cuando difieren exactamente en un vértice. Una descripción equivalente de H es que se forma dividiendo cada arista de G en un camino de dos aristas, y añadiendo un nuevo vértice conectado a todos los vértices originales de G . Este grafo H es por construcción un cubo parcial, pero es un grafo mediano sólo cuando G no tiene triángulos: si a , b y c forman un triángulo en G , entonces { a , b }, { a , c } y { b , c } no tienen mediana en H , ya que dicha mediana tendría que corresponder al conjunto { a , b , c }, pero los conjuntos de tres o más vértices de G no forman vértices en H . Por lo tanto, G no tiene triángulos si y solo si H es un grafo mediano. En el caso de que G no tenga triángulos, H es su grafo símplex . Un algoritmo para comprobar de manera eficiente si H es un grafo mediano también podría utilizarse con esta construcción para comprobar si G no tiene triángulos. Esta transformación preserva la complejidad computacional del problema, ya que el tamaño de H es proporcional al de G.
La reducción en la otra dirección, desde la detección de triángulos hasta la prueba de grafos medianos, es más compleja y depende del algoritmo de reconocimiento de grafos medianos anterior de Hagauer, Imrich y Klavžar (1999), que prueba varias condiciones necesarias para grafos medianos en tiempo casi lineal. El nuevo paso clave implica utilizar una búsqueda en amplitud para dividir los vértices del grafo en niveles según sus distancias a algún vértice raíz elegido arbitrariamente, formando un grafo a partir de cada nivel en el que dos vértices sean adyacentes si comparten un vecino común en el nivel anterior, y buscando triángulos en estos grafos. La mediana de cualquier triángulo de este tipo debe ser un vecino común de los tres vértices del triángulo; si este vecino común no existe, el grafo no es un grafo mediano. Si todos los triángulos encontrados de esta manera tienen medianas, y el algoritmo anterior descubre que el grafo satisface todas las demás condiciones para ser un grafo mediano, entonces debe ser en realidad un grafo mediano. Este algoritmo requiere, no solo la capacidad de comprobar si existe un triángulo, sino una lista de todos los triángulos en el gráfico de nivel. En gráficos arbitrarios, enumerar todos los triángulos a veces requiere Ω( m 3/2 ) de tiempo, ya que algunos gráficos tienen esa cantidad de triángulos; sin embargo, Hagauer et al. muestran que la cantidad de triángulos que surgen en los gráficos de nivel de su reducción es casi lineal, lo que permite utilizar la técnica de Alon et al. basada en la multiplicación rápida de matrices para encontrar triángulos.
La filogenia es la inferencia de árboles evolutivos a partir de características observadas de las especies ; un árbol de este tipo debe colocar las especies en vértices distintos y puede tener vértices latentes adicionales , pero se requiere que los vértices latentes tengan tres o más aristas incidentes y también deben estar etiquetados con características. Una característica es binaria cuando solo tiene dos valores posibles, y un conjunto de especies y sus características exhiben una filogenia perfecta cuando existe un árbol evolutivo en el que los vértices (especies y vértices latentes) etiquetados con cualquier valor característico particular forman un subárbol contiguo. Si no es posible un árbol con filogenia perfecta, a menudo se desea encontrar uno que exhiba máxima parsimonia o, equivalentemente, que minimice el número de veces que los puntos finales de una arista del árbol tienen valores diferentes para una de las características, sumados sobre todas las aristas y todas las características.
Buneman (1971) describió un método para inferir filogenias perfectas para características binarias, cuando existen. Su método se generaliza naturalmente a la construcción de un grafo mediano para cualquier conjunto de especies y características binarias, que se ha llamado red mediana o grafo de Buneman [24] y es un tipo de red filogenética . Cada árbol evolutivo de máxima parsimonia se incrusta en el grafo de Buneman, en el sentido de que los bordes del árbol siguen caminos en el grafo y el número de cambios de valores característicos en el borde del árbol es el mismo que el número en el camino correspondiente. El grafo de Buneman será un árbol si y solo si existe una filogenia perfecta; esto sucede cuando no hay dos características incompatibles para las que se observen las cuatro combinaciones de valores característicos.
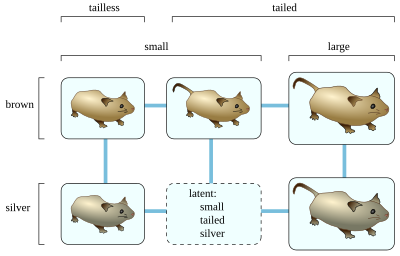
Para formar el gráfico de Buneman para un conjunto de especies y características, primero, elimine las especies redundantes que son indistinguibles de otras especies y las características redundantes que siempre son iguales a alguna otra característica. Luego, forme un vértice latente para cada combinación de valores característicos de modo que cada dos de los valores existan en alguna especie conocida. En el ejemplo que se muestra, hay ratones pequeños de color marrón sin cola, ratones pequeños de color plateado sin cola, ratones pequeños de cola marrón, ratones grandes de cola marrón y ratones grandes de cola plateada; el método del gráfico de Buneman formaría un vértice latente correspondiente a una especie desconocida de ratones pequeños de cola plateada, porque cada combinación de pares (pequeños y plateados, pequeños y con cola, y plateados y con cola) se observa en alguna otra especie conocida. Sin embargo, el método no inferiría la existencia de ratones grandes de color marrón sin cola, porque no se sabe que ningún ratón tenga tanto los rasgos grandes como los de no tener cola. Una vez que se determinen los vértices latentes, forme una arista entre cada par de especies o vértices latentes que difieran en una sola característica.
Se puede describir de manera equivalente una colección de características binarias como un sistema dividido , una familia de conjuntos que tiene la propiedad de que el conjunto complementario de cada conjunto en la familia también está en la familia. Este sistema dividido tiene un conjunto para cada valor característico, que consiste en las especies que tienen ese valor. Cuando se incluyen los vértices latentes, el sistema dividido resultante tiene la propiedad Helly : cada subfamilia que se interseca por pares tiene una intersección común. En cierto sentido, los grafos medianos se caracterizan por provenir de sistemas divididos Helly: los pares ( W uv , W vu ) definidos para cada arista uv de un grafo mediano forman un sistema dividido Helly, por lo que si se aplica la construcción del grafo Buneman a este sistema no se necesitarán vértices latentes y el resultado será el mismo que el grafo inicial. [25]
Bandelt et al. (1995) y Bandelt, Macaulay y Richards (2000) describen técnicas para el cálculo manual simplificado del gráfico de Buneman y utilizan esta construcción para visualizar las relaciones genéticas humanas.
