En matemáticas , especialmente en álgebra homológica y otras aplicaciones de la teoría de categorías abelianas , el lema de los cinco es un lema importante y ampliamente utilizado sobre diagramas conmutativos . El lema de los cinco no solo es válido para categorías abelianas, sino que también funciona en la categoría de grupos , por ejemplo.
Los cinco lemas pueden considerarse como una combinación de otros dos teoremas, los cuatro lemas , que son duales entre sí.
Considere el siguiente diagrama conmutativo en cualquier categoría abeliana (como la categoría de grupos abelianos o la categoría de espacios vectoriales sobre un cuerpo dado ) o en la categoría de grupos .
El quinto lema establece que, si las filas son exactas , m y p son isomorfismos , l es un epimorfismo y q es un monomorfismo , entonces n también es un isomorfismo.
Los dos cuatro lemas establecen:
El método de prueba que utilizaremos se conoce comúnmente como búsqueda de diagramas . [1] Probaremos los cinco lemas probando individualmente cada uno de los dos cuatro lemas.
Para realizar la búsqueda de diagramas, asumimos que estamos en una categoría de módulos sobre algún anillo , de modo que podemos hablar de elementos de los objetos en el diagrama y pensar en los morfismos del diagrama como funciones (de hecho, homomorfismos ) que actúan sobre esos elementos. Entonces un morfismo es un monomorfismo si y solo si es inyectivo , y es un epimorfismo si y solo si es sobreyectivo . De manera similar, para tratar con la exactitud, podemos pensar en núcleos e imágenes en un sentido de teoría de funciones. La prueba seguirá aplicándose a cualquier categoría abeliana (pequeña) debido al teorema de incrustación de Mitchell , que establece que cualquier categoría abeliana pequeña puede representarse como una categoría de módulos sobre algún anillo. Para la categoría de grupos, simplemente convierta toda la notación aditiva a continuación en notación multiplicativa y observe que la conmutatividad del grupo abeliano nunca se usa.
Entonces, para demostrar (1), supongamos que m y p son sobreyectivas y q es inyectiva.
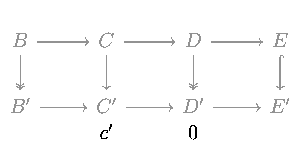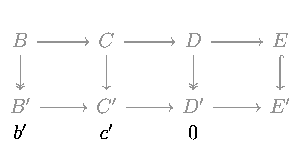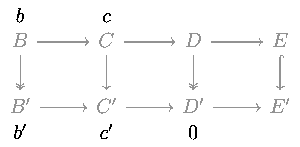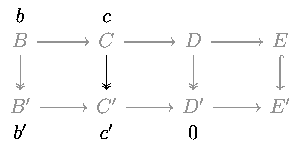

Luego, para demostrar (2), supongamos que m y p son inyectivas y l es sobreyectiva.

Combinando los dos cuatro lemas ahora se demuestra el quinto lema completo.
El lema de los cinco se aplica a menudo a secuencias largas y exactas : cuando se calcula la homología o cohomología de un objeto dado, normalmente se emplea un subobjeto más simple cuya homología/cohomología se conoce, y se llega a una secuencia larga y exacta que involucra los grupos de homología desconocidos del objeto original. Esto por sí solo no suele ser suficiente para determinar los grupos de homología desconocidos, pero si se pueden comparar el objeto y el subobjeto originales con otros bien conocidos mediante morfismos, entonces se induce un morfismo entre las respectivas secuencias largas y exactas, y entonces se puede utilizar el lema de los cinco para determinar los grupos de homología desconocidos.