Efecto Jahn-Teller

Mecanismo de ruptura espontánea de la simetría

El efecto Jahn-Teller (efecto JT o JTE) es un importante mecanismo de ruptura espontánea de la simetría en sistemas moleculares y de estado sólido que tiene consecuencias de gran alcance en diferentes campos y es responsable de una variedad de fenómenos en espectroscopia , estereoquímica , química de cristales , física molecular y del estado sólido y ciencia de los materiales . El efecto recibe su nombre de Hermann Arthur Jahn y Edward Teller , quienes informaron por primera vez sobre sus estudios en 1937.

Visión general simplificada

El efecto Jahn-Teller , también conocido como distorsión de Jahn-Teller , describe la distorsión geométrica de las moléculas y los iones que resulta de ciertas configuraciones electrónicas. El teorema de Jahn-Teller establece básicamente que cualquier molécula no lineal con un estado electrónico fundamental degenerado espacialmente sufrirá una distorsión geométrica que elimina esa degeneración, porque la distorsión reduce la energía general de la especie. Para una descripción de otro tipo de distorsión geométrica que ocurre en cristales con impurezas sustitucionales, consulte el artículo sobre iones descentrados .

Química de los metales de transición

El efecto Jahn-Teller es responsable de la distorsión tetragonal del complejo iónico hexaaquacobre(II), [Cu(OH ₂ ) ₆ ] ²⁺ , que de otro modo podría poseer una geometría octaédrica regular . Las dos distancias axiales de Cu−O son 238 pm , mientras que las cuatro distancias ecuatoriales de Cu−O son ~195 pm. Esta geometría es común en las estructuras cristalinas ; la geometría en solución es incierta. ^[1]

Arriba : el efecto JT se observa como elongación y compresión tetragonal en complejos octaédricos de alto espín d ⁴ debido al cambio neto en la energía de los electrones (observe la cantidad impar de electrones en el orbital e _g ). Abajo : el efecto JT no ocurre si no hay un cambio neto en la energía (observe la cantidad par de electrones en el orbital _{e g} ).

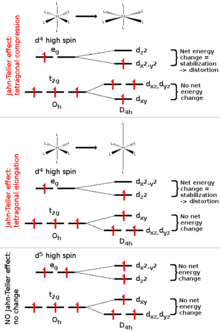
El efecto Jahn-Teller se encuentra con mayor frecuencia en complejos octaédricos de metales de transición. ^[2] El fenómeno es muy común en complejos de cobre (II) de seis coordenadas. ^[3] La configuración electrónica d ^{9 de este} ion da tres electrones en los dos orbitales e g degenerados , lo que conduce a un estado fundamental electrónico doblemente degenerado. Estos complejos se distorsionan a lo largo de uno de los ejes cuádruples moleculares (siempre etiquetado como el eje z ), lo que tiene el efecto de eliminar las degeneraciones orbitales y electrónicas y reducir la energía general. La distorsión normalmente toma la forma de alargamiento de los enlaces a los ligandos que se encuentran a lo largo del eje z , pero ocasionalmente ocurre como un acortamiento de estos enlaces (el teorema de Jahn-Teller no predice la dirección de la distorsión, solo la presencia de una geometría inestable). Cuando se produce una elongación de este tipo, el efecto es reducir la repulsión electrostática entre el par de electrones del ligando básico de Lewis y cualquier electrón en orbitales con un componente z , lo que reduce la energía del complejo. El centro de inversión se conserva después de la distorsión.

En los complejos octaédricos, el efecto Jahn-Teller es más pronunciado cuando un número impar de electrones ocupa los orbitales e _g . Esta situación surge en complejos con las configuraciones d ⁹ , d ⁷ de bajo espín o d ⁴ de alto espín , todos los cuales tienen estados fundamentales doblemente degenerados. En tales compuestos, los orbitales e _g involucrados en la degeneración apuntan directamente a los ligandos, por lo que la distorsión puede resultar en una gran estabilización energética. Estrictamente hablando, el efecto también ocurre cuando hay una degeneración debido a los electrones en los orbitales t _2g ( es decir, configuraciones como d ¹ o d ² , ambas triplemente degeneradas). En tales casos, sin embargo, el efecto es mucho menos notable, porque hay una disminución mucho menor de la repulsión al alejar los ligandos de los orbitales t _2g , que no apuntan directamente a los ligandos (ver la tabla siguiente). Lo mismo ocurre en los complejos tetraédricos (por ejemplo, el manganato) : la distorsión es muy sutil porque se puede lograr menos estabilización debido a que los ligandos no apuntan directamente a los orbitales.

Los efectos esperados para la coordinación octaédrica se dan en la siguiente tabla:

w: efecto Jahn-Teller débil ( los orbitales t _2g están ocupados de forma desigual)

s: se espera un fuerte efecto Jahn-Teller ( por _ejemplo, orbitales ocupados de manera desigual)

en blanco: no se espera efecto Jahn-Teller.

El efecto Jahn-Teller se manifiesta en los espectros de absorbancia UV-VIS de algunos compuestos, donde a menudo provoca la división de bandas. Es fácilmente evidente en las estructuras de muchos complejos de cobre(II). ^{[4] Sin embargo, se puede obtener información adicional y detallada sobre la anisotropía de dichos complejos y la naturaleza de la unión del ligando a partir de la estructura fina de los espectros} de resonancia de espín electrónico a baja temperatura .

El efecto Jahn-Teller obliga al anión radical del ciclooctatetraeno (−1) a ser asimétrico (ver texto)

Efectos relacionados

La causa subyacente del efecto Jahn-Teller es la presencia de orbitales moleculares degenerados y de capa abierta (es decir, ocupados de forma incompleta). Esta situación no es exclusiva de los complejos de coordinación y puede encontrarse en otras áreas de la química. En la química orgánica, el fenómeno de la antiaromaticidad tiene la misma causa y también suele provocar la distorsión de las moléculas, como en el caso del ciclobutadieno ^[5] y el ciclooctatetraeno (COT). ^[6]

Tratamiento avanzado

El teorema de Jahn-Teller

El teorema JT se puede enunciar de diferentes formas, dos de las cuales se dan aquí:

"Un sistema poliatómico no lineal en un estado electrónico espacialmente degenerado se distorsiona espontáneamente de tal manera que la degeneración se levanta y se alcanza una nueva estructura de equilibrio de menor simetría".

Alternativamente y considerablemente más corto:

"... la estabilidad y la degeneración no son posibles simultáneamente a menos que la molécula sea lineal...". ^[7]

La degeneración del espín fue una excepción en el tratamiento original y luego se trató por separado. ^[8]

La prueba matemática formal del teorema de Jahn-Teller se basa en gran medida en argumentos de simetría, más específicamente en la teoría de grupos puntuales moleculares . El argumento de Jahn y Teller no presupone ningún detalle sobre la estructura electrónica del sistema. Jahn y Teller no hicieron ninguna afirmación sobre la intensidad del efecto, que puede ser tan pequeña que sea inmensurable. De hecho, para los electrones en orbitales moleculares no enlazantes o de enlace débil , se espera que el efecto sea débil. Sin embargo, en muchas situaciones el efecto JT es importante.

Acontecimientos históricos

El interés en el JTE aumentó después de su primera verificación experimental. Se desarrollaron varios sistemas modelo para investigar el grado de degeneración y el tipo de simetría. ^[9] Estos se resolvieron en parte analíticamente y en parte numéricamente para obtener la forma de las superficies de energía potencial (PES) pertinentes y los niveles de energía para el movimiento nuclear en la PES dividida por JT. Estos niveles de energía no son niveles de energía vibracional en el sentido tradicional debido al intrincado acoplamiento con el movimiento electrónico que ocurre, y se denominan mejor niveles de energía vibrónicos . Nació el nuevo campo del " acoplamiento vibrónico " o "teoría del acoplamiento vibrónico".

Otro gran avance se produjo con la aparición de los cálculos de estructura electrónica modernos (" ab initio ") , mediante los cuales los parámetros relevantes que caracterizan los sistemas JT pueden determinarse de manera fiable a partir de los primeros principios. De este modo, se pudo ir más allá de los estudios de sistemas modelo que exploran el efecto de las variaciones de parámetros en los niveles de energía PES y vibrónica ; también se pudo ir más allá del ajuste de estos parámetros a los datos experimentales sin un conocimiento claro sobre la importancia del ajuste. En cambio, se hicieron posibles investigaciones teóricas bien fundamentadas que mejoraron enormemente la comprensión de los fenómenos en cuestión y de los detalles de los mecanismos subyacentes.

Comparación conceptual de los efectos Jahn-Teller y pseudo-Jahn-Teller, que muestra la relación mutua de dos superficies de energía potencial (PES) en los dos casos. El número de PES es dos en esta imagen, pero puede ser mayor en sistemas moleculares o de estado sólido reales.

Si bien se reconoce la distorsión JTE como un ejemplo concreto del mecanismo general de ruptura espontánea de la simetría , la degeneración exacta del estado electrónico involucrado se identificó como un ingrediente no esencial para esta ruptura de la simetría en sistemas poliatómicos. Incluso los sistemas que en la configuración simétrica no distorsionada presentan estados electrónicos que son cercanos en energía pero no precisamente degenerados, pueden mostrar una tendencia similar a la distorsión. Las distorsiones de estos sistemas pueden tratarse dentro de la teoría relacionada del efecto pseudo Jahn-Teller (en la literatura a menudo denominado "JTE de segundo orden"). Este mecanismo está asociado a los acoplamientos vibrónicos entre PES adiabáticos separados por brechas de energía no nulas a través del espacio de configuración: su inclusión extiende la aplicabilidad de los modelos relacionados con JT a la ruptura de la simetría en una gama mucho más amplia de sistemas moleculares y de estado sólido.

Cronología:

• 1934: Lev Landau , en discusión con Edward Teller , sugirió que los estados electrónicos de ciertas configuraciones nucleares degeneradas son inestables con respecto a los desplazamientos nucleares que reducen la simetría (ver 'Una nota histórica' de Englman ^[10] ).
• 1937: Hermann Arthur Jahn y Edward Teller formularon lo que ahora se conoce como el teorema de Jahn-Teller. ^[7]
• 1939: John Hasbrouck Van Vleck amplió el teorema de Jahn-Teller a los iones en cristales. Como los intentos de observar el efecto Jahn-Teller experimentalmente no habían sido convincentes, señaló que "el gran mérito del efecto Jahn-Teller es que desaparece cuando no se lo necesita". ^{[11] [12]}
• 1950–2: Brebis Bleaney y sus colaboradores obtuvieron por primera vez evidencia experimental inequívoca del efecto Jahn-Teller, al realizar estudios de resonancia paramagnética electrónica sobre iones paramagnéticos en cristales ^{[13] [14]}
• 1957–8: Öpik y Pryce demostraron que el acoplamiento espín-órbita puede estabilizar configuraciones simétricas contra distorsiones de un JTE débil. ^[15] Moffitt et al. ^{[16] [17]} y Longuet-Higgins et al. ^[18] argumentaron que los estados de los sistemas JT tienen componentes electrónicos y vibracionales inextricablemente mezclados, a los que llamaron estados vibrónicos , con energías muy diferentes a los estados electrónicos.
• 1962–4: Isaac Bersuker ^[19] y Mary O'Brien ^[20] investigaron la tunelización en los estados vibrónicos de energía más baja , la denominada división por tunelización, y la naturaleza dinámica del efecto JT. El artículo de O'Brien muestra la influencia del factor de fase geométrica (posteriormente llamado fase de Berry) en el ordenamiento de los estados vibrónicos.
• 1965: Frank Ham se dio cuenta del efecto de la dinámica coherente en la medición de observables. Esta influencia puede describirse en términos de factores de reducción que multiplican los operadores orbitales ^[21] y se propusieron fórmulas específicas para el magnetismo de los iones JT.
• 1984: La generalización del concepto de fase geométrica de Berry ^[22] (o fase de Berry como también se la conoce) proporcionó una base general para ayudar a comprender la fase dependiente de la rotación asociada con la función de onda electrónica y vibracional de los sistemas JT, como lo descubrieron Longuet-Higgins, ^[18] y discutieron más a fondo Herzberg y Longuet-Higgins, ^[23] Longuet-Higgins, ^[24] O'Brien, ^[20] y Mead y Truhlar. ^[25]
• Década de 1990: Los avances en el poder de cómputo significaron que se empezaron a utilizar métodos ab initio, incluidos aquellos basados ​​en la teoría del funcional de la densidad, para resolver problemas JT.

Relación con descubrimientos importantes

• En 1985, Harry Kroto y sus colaboradores descubrieron una clase de moléculas de carbono de jaula cerrada conocidas como fulerenos . ^[26] El buckminsterfullereno (C ₆₀ ), que tiene simetría icosaédrica , se vuelve JT-activo tras la adición o eliminación de un electrón. ^[27] El orden de los niveles de energía puede no ser el mismo que el predicho por la regla de Hund .
• El descubrimiento en 1986 por Bednorz y Müller de la superconductividad en cupratos con una temperatura de transición de 35 K, ^[28] que era más alta que el límite superior permitido según la teoría BCS estándar, fue motivado por el trabajo anterior de Müller sobre iones JT en cristales.
• La magnetorresistencia colosal , una propiedad de las perovskitas basadas en manganeso y otros materiales, se ha explicado en términos de competencia entre los efectos dinámicos de Jahn-Teller y de doble intercambio. ^[29]
• El teorema de Peierls , que establece que una cadena unidimensional de iones igualmente espaciados con un electrón por ion es inestable, tiene raíces comunes con el efecto JT.

Teoría

Simetría de sistemas JT y categorización utilizando teoría de grupos

Un problema JT dado tendrá una simetría de grupo puntual particular , como la simetría T d para iones de impurezas magnéticas en semiconductores o la simetría I h para el fulereno C ₆₀ . Los problemas JT se clasifican convencionalmente utilizando etiquetas para las representaciones irreducibles (irreps) que se aplican a la simetría de los estados electrónicos y vibracionales. Por ejemplo, E ⊗ e se referiría a un estado doblete electrónico que se transforma como E acoplado a un estado doblete vibracional que se transforma como e.

En general, un modo vibracional que se transforma como Λ se acoplará a un estado electrónico que se transforma como Γ si la parte simétrica del producto de Kronecker [Γ ⊗ Γ] _S contiene Λ, a menos que Γ sea una representación de doble grupo cuando se considera en cambio la parte antisimétrica {Γ ⊗ Γ} _A. Los modos que se acoplan se denominan JT-activos.

Como ejemplo, considere un estado electrónico doblete E en simetría cúbica. La parte simétrica de E ⊗ E es A ₁ + E. Por lo tanto, el estado E se acoplará a modos vibracionales que se transforman como a ₁ y e. Sin embargo, los modos a ₁ darán como resultado el mismo cambio de energía a todos los estados y, por lo tanto, no contribuyen a ninguna división JT. Por lo tanto, se pueden descuidar. El resultado es un efecto JT E ⊗ e. Este efecto JT lo experimentan las moléculas triangulares X ₃ , las moléculas tetraédricas ML ₄ y las moléculas octaédricas ML ₆ cuando su estado electrónico tiene simetría E. ${\displaystyle Q_{i}}$

Los componentes de un modo vibracional determinado también se etiquetan según sus propiedades de transformación. Por ejemplo, los dos componentes de un modo e suelen etiquetarse como y , que en simetría octaédrica se transforman como y respectivamente. ${\displaystyle Q_{\theta }}$ ${\displaystyle Q_{\epsilon }}$ ${\displaystyle 3z^{2}-r^{2}}$ ${\displaystyle x^{2}-y^{2}}$

El hamiltoniano JT

Los valores propios del hamiltoniano de un sistema poliatómico definen los PES como funciones de los modos normales del sistema (es decir, combinaciones lineales de los desplazamientos nucleares con propiedades de simetría específicas). En el punto de referencia de alta simetría, donde ocurre la degeneración inducida por la simetría, varios de los valores propios coinciden. Mediante un análisis detallado y laborioso, Jahn y Teller demostraron que, a excepción de las moléculas lineales, siempre hay términos de primer orden en una expansión de los elementos de la matriz del hamiltoniano en términos de modos normales de reducción de la simetría (en el lenguaje de la teoría de grupos : no totalmente simétricos). Estos términos lineales representan fuerzas que distorsionan el sistema a lo largo de estas coordenadas y elevan la degeneración. Por lo tanto, el punto de degeneración no puede ser estacionario y el sistema se distorsiona hacia un punto estacionario de menor simetría donde se puede alcanzar la estabilidad. ${\displaystyle Q_{i}}$

La demostración del teorema JT se desprende de la teoría de la simetría molecular ( teoría de grupos puntuales ). En la sección § Química de coordinación se ofrece una explicación menos rigurosa pero más intuitiva .

Para llegar a una descripción cuantitativa del efecto JT, las fuerzas que aparecen entre las funciones de onda componentes se describen expandiendo el hamiltoniano en una serie de potencias en el . Debido a la naturaleza misma de la degeneración, el hamiltoniano toma la forma de una matriz que hace referencia a los componentes de la función de onda degenerada . Un elemento de matriz entre estados y generalmente se lee como: ${\displaystyle Q_{i}}$ ${\displaystyle \Psi _{a}}$ ${\displaystyle \Psi _{b}}$

${\displaystyle H_{ab}=\langle \Psi _{a}|H|\Psi _{b}\rangle =\langle \Psi _{a}|H(Q_{i}=0)+\sum _{i}{\frac {\partial V}{\partial Q_{i}}}Q_{i}+...|\Psi _{b}\rangle }$

La expansión se puede truncar después de los términos lineales en el , o extender para incluir términos cuadráticos (o superiores) en el . ${\displaystyle Q_{i}}$ ${\displaystyle Q_{i}}$

Las superficies de energía potencial adiabática (APES) se obtienen entonces como valores propios de esta matriz. En el artículo original se demuestra que siempre hay términos lineales en la expansión. De ello se deduce que la degeneración de la función de onda no puede corresponder a una estructura estable.

Superficies de energía potencial

Potencial del sombrero mexicano

En términos matemáticos, los APES que caracterizan la distorsión JT surgen como los valores propios de la matriz de energía potencial. Generalmente, los APES toman la apariencia característica de un cono doble, circular o elíptico, donde el punto de contacto, es decir, la degeneración, denota la configuración de alta simetría para la que se aplica el teorema JT. Para el caso anterior del efecto JT lineal E ⊗ e, la situación se ilustra mediante los APES

${\displaystyle V={\frac {\mu \omega ^{2}}{2}}(Q_{\theta }^{2}+Q_{\epsilon }^{2})\pm k{\sqrt {Q_{\theta }^{2}+Q_{\epsilon }^{2}}}}$

Se muestra en la figura, con una parte cortada para revelar su forma, que se conoce como potencial de sombrero mexicano. Aquí, es la frecuencia del modo vibracional e, es su masa y es una medida de la fuerza del acoplamiento JT. ${\displaystyle \omega }$ ${\displaystyle \mu }$ ${\displaystyle k}$

Las superficies de energía potencial de un efecto Jahn-Teller E ⊗ e

La forma cónica cerca de la degeneración en el origen deja en claro inmediatamente que este punto no puede ser estacionario , es decir, el sistema es inestable frente a distorsiones asimétricas, lo que conduce a una disminución de la simetría. En este caso particular, hay infinitas distorsiones isoenergéticas JT. Las distorsiones resultantes están dispuestas en un círculo, como lo muestra la curva roja en la figura. El acoplamiento cuadrático o los términos elásticos cúbicos conducen a una deformación a lo largo de este "camino de energía mínima", reemplazando esta variedad infinita por tres mínimos potenciales equivalentes y tres puntos de silla equivalentes. En otros sistemas JT, el acoplamiento lineal da como resultado mínimos discretos. ${\displaystyle Q_{i}}$

Intersecciones cónicas

La alta simetría de la topología de doble cono del sistema lineal E ⊗ e JT refleja directamente la alta simetría subyacente. Es uno de los primeros ejemplos (si no el primero) en la literatura de una intersección cónica de superficies de energía potencial. Las intersecciones cónicas han recibido una amplia atención en la literatura a partir de la década de 1990 y ahora se consideran paradigmas de la dinámica de estados excitados no adiabáticos, con consecuencias de largo alcance en la espectroscopia molecular, la fotoquímica y la fotofísica. Algunas de ellas se comentarán más adelante. En general, las intersecciones cónicas son mucho menos simétricas que las representadas en la figura. Pueden estar inclinadas y tener forma elíptica, etc., y también se han distinguido en la literatura intersecciones con picos y en pendiente. Además, para más de dos grados de libertad, no son estructuras puntuales sino costuras e hipersuperficies curvas complicadas, también conocidas como espacio de intersección. El subespacio de coordenadas que se muestra en la figura también se conoce como plano de ramificación.

Implicaciones para la dinámica

La forma característica de la APES dividida por JT tiene consecuencias específicas para la dinámica nuclear, considerada aquí en sentido plenamente cuántico. Para un acoplamiento JT suficientemente fuerte, los puntos mínimos están suficientemente lejos (al menos unos cuantos de energía vibracional) por debajo de la intersección JT. Se pueden distinguir entonces dos regímenes de energía diferentes, el de baja y el de alta energía.

• En el régimen de baja energía, el movimiento nuclear se limita a regiones cercanas a los "puntos de energía mínima". Las configuraciones distorsionadas muestreadas imparten sus parámetros geométricos, por ejemplo, a la estructura fina rotacional en un espectro. Debido a la existencia de barreras entre los diversos mínimos en el APES, como las que aparecen debido a la deformación del (véase § Potencial de sombrero mexicano) , el movimiento en el régimen de baja energía suele clasificarse como un JTE estático, un JTE dinámico o un salto incoherente. Cada régimen muestra huellas particulares en las mediciones experimentales.

• JTE estático : en este caso, el sistema está atrapado en uno de los mínimos de energía más bajos del APES (normalmente determinado por pequeñas perturbaciones creadas por el entorno del sistema JT) y no tiene suficiente energía para cruzar la barrera hacia otro mínimo durante el tiempo típico asociado a la medición. Los efectos dinámicos cuánticos, como el efecto túnel, son despreciables y, efectivamente, la molécula o el sólido muestran la baja simetría asociada con un único mínimo.

• JTE dinámico : ^[30] En este caso, las barreras son suficientemente pequeñas comparadas con, por ejemplo, la energía de punto cero asociada a los mínimos, de modo que las funciones de onda vibrónicas (y todos los observables) muestran la simetría del sistema de referencia (sin distorsión). En el problema lineal E ⊗ e, el movimiento asociado a este régimen sería alrededor de la trayectoria circular en la figura. Cuando la barrera es suficientemente pequeña, esto se llama pseudorotación (libre) (no debe confundirse con la rotación de un cuerpo rígido en el espacio, vea la diferencia entre rotaciones reales y pseudo ilustradas aquí para la molécula de fulereno C ₆₀ ). Cuando la barrera entre los mínimos y los puntos de silla en la trayectoria deformada excede un quantum vibracional, el movimiento pseudorotacional se ralentiza y ocurre a través de un túnel. Esto se llama pseudorotación impedida. Tanto en la pseudorotación libre como en la impedida, el fenómeno importante de la fase geométrica (Berry) altera el orden de los niveles.

• Salto incoherente : Otra forma en la que el sistema puede superar la barrera es a través de la energía térmica. En este caso, mientras el sistema se mueve a lo largo de los mínimos del sistema, el estado no es coherente cuánticamente sino una mezcla estadística. Esta diferencia se puede observar experimentalmente.

• La dinámica es bastante diferente para energías altas, como ocurre a partir de una transición óptica desde un estado inicial no degenerado con una geometría de equilibrio de alta simetría (JT no distorsionada) a un estado JT distorsionado. Esto lleva al sistema a la región cerca de la intersección cónica del APES dividido por JT en el centro de la figura. Aquí los acoplamientos no adiabáticos se vuelven muy grandes y el comportamiento del sistema no se puede describir dentro de la separación familiar de Born-Oppenheimer (BO) entre los movimientos electrónicos y nucleares. El movimiento nuclear deja de estar confinado a un único APES bien definido y las transiciones entre las superficies adiabáticas ocurren produciendo efectos como resonancias de Slonzcewsky. En las moléculas, esto suele ser una escala de tiempo de femtosegundos, lo que equivale a procesos de conversión interna ultrarrápidos (femtosegundos), acompañados de amplias bandas espectrales también en condiciones de molécula aislada y características espectrales altamente complejas. Se tratarán ejemplos de estos fenómenos en la sección § Espectroscopía y reactividad .

Como ya se ha indicado anteriormente, la distinción entre regímenes de energía baja y alta es válida únicamente para acoplamientos JT suficientemente fuertes, es decir, cuando varios o muchos cuantos de energía vibracional encajan en la ventana de energía entre la intersección cónica y el mínimo de los APES de división JT inferiores. Para los numerosos casos de acoplamientos JT pequeños a intermedios, esta ventana de energía y el correspondiente régimen adiabático de energía baja no existen. En cambio, los niveles en ambos APES de división JT están intrincadamente mezclados para todas las energías y el movimiento nuclear siempre se produce en ambos APES de división JT simultáneamente.

Factores del jamón

En 1965, Frank Ham ^[21] propuso que el JTE dinámico podría reducir los valores esperados de los observables asociados con las funciones de onda orbitales debido a la superposición de varios estados electrónicos en la función de onda vibrónica total. Este efecto conduce, por ejemplo, a una extinción parcial de la interacción espín-órbita ^{[21] [31]} y permitió explicar los resultados de experimentos previos de Resonancia Paramagnética Electrónica (EPR).

En general, el resultado de un operador orbital que actúa sobre estados vibrónicos puede ser reemplazado por un operador orbital efectivo que actúa sobre estados puramente electrónicos. En primer orden, el operador orbital efectivo es igual al operador orbital real multiplicado por una constante, cuyo valor es menor que uno, conocido como factor de reducción de primer orden (Ham). Por ejemplo, dentro de un estado electrónico triplete T ₁ , el operador de acoplamiento espín-órbita puede ser reemplazado por , donde es una función de la fuerza del acoplamiento JT que varía de 1 en acoplamiento cero a 0 en acoplamiento muy fuerte. Además, cuando se incluyen correcciones de perturbación de segundo orden, se introducen términos adicionales que involucran factores numéricos adicionales, conocidos como factores de reducción de segundo orden (Ham). Estos factores son cero cuando no hay acoplamiento JT pero pueden dominar sobre los términos de primer orden en acoplamiento fuerte, cuando los efectos de primer orden se han reducido significativamente. ^[9] ${\displaystyle \lambda \mathbf {L} .\mathbf {S} }$ ${\displaystyle \gamma \lambda \mathbf {L} .\mathbf {S} }$ ${\displaystyle \gamma }$

Los factores de reducción son particularmente útiles para describir resultados experimentales, como EPR y espectros ópticos, de impurezas paramagnéticas en hospedadores semiconductores , dieléctricos , diamagnéticos y ferromagnéticos .

Desarrollos modernos

Durante mucho tiempo, las aplicaciones de la teoría JT consistieron principalmente en estudios de parámetros (estudios de modelos) donde los APES y las propiedades dinámicas de los sistemas JT se han investigado como funciones de los parámetros del sistema, como las constantes de acoplamiento, etc. Los ajustes de estos parámetros a los datos experimentales a menudo eran dudosos y no concluyentes. La situación cambió en la década de 1980 cuando se desarrollaron métodos ab initio eficientes y los recursos computacionales se volvieron lo suficientemente poderosos como para permitir una determinación confiable de estos parámetros a partir de los primeros principios. ^[32] Además de las técnicas basadas en funciones de onda (que a veces se consideran genuinamente ab initio en la literatura), el advenimiento de la teoría del funcional de la densidad (DFT) abrió nuevas vías para tratar sistemas más grandes, incluidos los sólidos. Esto permitió caracterizar los detalles de los sistemas JT e interpretar los hallazgos experimentales de manera confiable. Se encuentra en el corazón de la mayoría de los desarrollos abordados en la sección § Aplicaciones .

Se pueden concebir dos estrategias diferentes que se han utilizado en la literatura. Una puede

1. dar por sentada la aplicabilidad de un determinado esquema de acoplamiento y limitarse a determinar los parámetros del modelo, por ejemplo a partir de la ganancia de energía lograda a través de la distorsión JT, también denominada energía de estabilización JT.
2. mapear partes del APES en su totalidad o en una dimensión reducida y así obtener una idea de la aplicabilidad del modelo, posiblemente también derivando ideas sobre cómo extenderlo.

Naturalmente, el enfoque más preciso (2) puede limitarse a sistemas más pequeños, mientras que el enfoque más simple (1) se presta a estudios de sistemas más grandes.

Aplicaciones

Efectos sobre la estructura

Moléculas pequeñas y iones

La distorsión JT de moléculas pequeñas (o iones moleculares) se deduce directamente de los cálculos de la estructura electrónica de sus APES (a través de DFT y/o cálculos ab initio). Estas moléculas/iones son a menudo radicales, como trímeros de átomos alcalinos (Li ₃ y Na ₃ ), que tienen espines desapareados y en particular en (pero no restringidos a) estados doblete. Además de la JTE en estados ² E' y ² E", también la pseudo JTE entre un estado E y un estado A cercano puede desempeñar un papel. La distorsión JT reduce la simetría de D _3h a C _2v (ver figura), y depende de los detalles de las interacciones si el triángulo isósceles tiene una estructura de energía mínima aguda u obtusa (como Na ₃ ). Las extensiones naturales son sistemas como NO ₃ y NH ₃ ⁺ donde una distorsión JT ha sido documentada en la literatura para estados electrónicos fundamentales o excitados.

Dos posibles formas en las que un triángulo equilátero podría distorsionarse debido a un efecto Jahn-Teller

_{Los sistemas tetraédricos como el CH 4} ⁺ y el P ₄ ⁺ desempeñan un papel un tanto especial . En ellos entran en juego los estados electrónicos y modos vibracionales degenerados triples. No obstante, también las degeneraciones dobles siguen siendo importantes. La dinámica de la distorsión de Jahn-Teller en el CH ₄ ⁺ se ha caracterizado mediante espectroscopia de absorción transitoria de rayos X, revelando que la ruptura de la simetría se produce en diez femtosegundos en este sistema prototípico. ^[33]

Entre los sistemas más grandes, la literatura se ha centrado en el benceno y su catión radical, así como en sus derivados de halo (especialmente flúor). Ya a principios de la década de 1980, surgió una gran cantidad de información del análisis detallado de los espectros de emisión experimentales de los cationes radicales 1,3,5-trifluoro- y hexafluoro (y cloro) benceno. Para el catión benceno original, uno tiene que confiar en los espectros de fotoelectrones con una resolución comparativamente menor porque esta especie no fluoresce (ver también la sección § Espectroscopia y reactividad ). Se han realizado cálculos ab initio bastante detallados que documentan las energías de estabilización de JT para los diversos (cuatro) modos activos de JT y también cuantifican las barreras moderadas para la pseudorotación de JT.

Por último, los sistemas con un eje de simetría quíntuple, como el radical ciclopentadienilo, desempeñan un papel un tanto especial. Las cuidadosas investigaciones espectroscópicas láser han arrojado luz útil sobre las interacciones JT. En particular, revelan que la barrera a la pseudorrotación prácticamente desaparece (el sistema es altamente "fluxional"), lo que puede atribuirse al hecho de que los términos de acoplamiento de segundo orden desaparecen por simetría y los términos principales de orden superior son de cuarto orden.

Química de coordinación

El JTE suele ser más fuerte allí donde la densidad electrónica asociada a los orbitales degenerados está más concentrada. Por lo tanto, este efecto desempeña un papel importante en la determinación de la estructura de los complejos de metales de transición con orbitales 3D internos activos.

Imágenes de orbitales d transformándose como e incrustados en un octaedro ${\displaystyle 3z^{2}-r^{2}}$ ${\displaystyle x^{2}-y^{2}}$

Efecto de una distorsión JT sobre los orbitales d

El más icónico y prominente de los sistemas JT en la química de coordinación es probablemente el caso de los complejos octaédricos de Cu(II). Mientras que en coordinación perfectamente equivalente, como un complejo CuF ₆ asociado a una impureza Cu(II) en un cristal cúbico como KMgF ₃ , se espera una simetría octaédrica (O _h ) perfecta. De hecho, una simetría tetragonal menor se encuentra generalmente experimentalmente. El origen de esta distorsión JTE se reveló al examinar la configuración electrónica del complejo no distorsionado. Para una geometría octaédrica, los cinco orbitales 3d se dividen en orbitales t _2g y e _g (ver diagrama). Estos orbitales están ocupados por nueve electrones correspondientes a la configuración electrónica de Cu(II). Por lo tanto, la capa t _2g está llena, y la capa e _{g contiene 3 electrones. En general, el electrón desapareado produce un estado} ² E _g , que es activo de Jahn-Teller. El tercer electrón puede ocupar cualquiera de los orbitales que comprenden la capa e _g : el orbital principalmente o el orbital principalmente. Si el electrón ocupa el nivel principalmente, ¿qué orbital antienlazante? La geometría final del complejo se alargaría ya que los ligandos axiales se alejarían para reducir la energía global del sistema. Por otro lado, si el electrón entrara en el orbital principalmente antienlazante, el complejo se distorsionaría en una geometría comprimida. Experimentalmente, se observan geometrías alargadas abrumadoramente y este hecho se ha atribuido tanto a interacciones anarmónicas metal-ligando ^[15] como a hibridaciones 3d-4s. ^[34] Dado que todas las direcciones que contienen un eje cuádruple son equivalentes, la distorsión es igualmente probable que ocurra en cualquiera de estas orientaciones. Desde el punto de vista electrónico, esto significa que los orbitales y , que son degenerados y libres de hibridar en la geometría octaédrica, se mezclarán para producir orbitales equivalentes apropiados en cada dirección como o . ${\displaystyle d^{9}}$ ${\displaystyle 3z^{2}-r^{2}}$ ${\displaystyle x^{2}-y^{2}}$ ${\displaystyle 3z^{2}-r^{2}}$ ${\displaystyle x^{2}-y^{2}}$ ${\displaystyle 3z^{2}-r^{2}}$ ${\displaystyle x^{2}-y^{2}}$ ${\displaystyle 3x^{2}-r^{2}}$ ${\displaystyle 3y^{2}-r^{2}}$

La JTE no se limita a los complejos octaédricos de Cu(II). Existen muchas otras configuraciones, que implican cambios tanto en la estructura inicial como en la configuración electrónica del metal que dan lugar a estados degenerados y, por tanto, a JTE. Sin embargo, la cantidad de distorsión y energía de estabilización del efecto depende en gran medida del caso particular. En el Cu(II) octaédrico, la JTE es particularmente fuerte porque

1. Los orbitales degenerados muestran un carácter σ fuertemente antienlazante.
2. El Cu es un metal de transición con una electronegatividad relativamente fuerte que produce más enlaces covalentes que otros metales, lo que permite aumentar la constante de acoplamiento lineal JT.

En otras configuraciones que implican enlaces π o δ, como por ejemplo cuando el estado degenerado está asociado a los orbitales t _2g de una configuración octaédrica, las energías de distorsión y estabilización suelen ser mucho menores y la posibilidad de no observar la distorsión debida a los efectos dinámicos del JTE es mucho mayor. De manera similar, para los iones de tierras raras donde la covalencia es muy pequeña, las distorsiones asociadas al JTE suelen ser muy débiles.

Es importante destacar que el JTE está asociado con una degeneración estricta en el subsistema electrónico y, por lo tanto, no puede aparecer en sistemas sin esta propiedad. Por ejemplo, el JTE se asocia a menudo a casos como complejos cuasi octaédricos CuX ₂ Y ₄ donde las distancias a los ligandos X e Y son claramente diferentes. Sin embargo, la simetría intrínseca de estos complejos ya es tetragonal y no existe ningún orbital e _g degenerado , habiéndose dividido en orbitales a _1g (principalmente ) y b _1g (principalmente ) debido a las diferentes interacciones electrónicas con los ligandos X axiales y los ligandos Y ecuatoriales . En este y otros casos similares, algunos efectos vibrónicos restantes relacionados con el JTE todavía están presentes, pero se extinguen con respecto al caso con degeneración debido a la división de los orbitales. ${\displaystyle 3z^{2}-r^{2}}$ ${\displaystyle x^{2}-y^{2}}$

Espectroscopia y reactividad

A partir de espectros con resolución rotacional, los momentos de inercia y, por lo tanto, las longitudes y ángulos de enlace se pueden determinar "directamente" (al menos en principio). A partir de espectros menos resueltos, aún se pueden determinar cantidades importantes como las energías de estabilización JT y las barreras de energía (por ejemplo, a la pseudorotación). Sin embargo, en toda la distribución de intensidad espectral de una transición electrónica se codifica más información. Se ha utilizado para decidir sobre la presencia (o ausencia) de la fase geométrica que se acumula durante el movimiento pseudorrotacional alrededor de la intersección cónica JT (u otro tipo de). Ejemplos destacados de ambos tipos son el estado fundamental (X) o un estado excitado (B) de Na ₃ . La transformada de Fourier de , la llamada función de autocorrelación, refleja el movimiento del paquete de ondas después de una transición óptica (= vertical) al APES del estado electrónico final. Normalmente se moverá en la escala de tiempo de un período vibracional que es (para moléculas pequeñas) del orden de 5-50 fs, es decir, ultrarrápido. Además de un movimiento casi periódico, también pueden producirse interacciones entre modos con un comportamiento muy irregular (también caótico) y una dispersión del paquete de ondas. Cerca de una intersección cónica, esto estará acompañado/complementado por transiciones no radiativas (denominadas conversión interna) a otros APES que se producen en la misma escala de tiempo ultrarrápida. ${\displaystyle P(E)}$ ${\displaystyle P(E)}$ ${\displaystyle C(t)}$

En el caso del JT, la situación es algo especial, en comparación con una intersección cónica general, porque las diferentes capas de potencial del JT están relacionadas entre sí por simetría y tienen (exactamente o casi) el mismo mínimo de energía. La "transición" entre ellas es, por lo tanto, más oscilatoria de lo que cabría esperar normalmente, y sus poblaciones promediadas en el tiempo son cercanas a 1/2. Para un escenario más típico, se "requiere" una intersección cónica más general.

El efecto JT sigue entrando en juego, concretamente en combinación con un estado electrónico cercano diferente, en general no degenerado. El resultado es un pseudo efecto Jahn-Teller , por ejemplo, de un estado E que interactúa con un estado A. Esta situación es común en los sistemas JT, al igual que las interacciones entre dos estados electrónicos no degenerados son comunes para los sistemas no JT. Ejemplos de ello son los estados electrónicos excitados de NH ₃ ⁺ y el catión radical benceno. Aquí, los cruces entre los APES de estado E y A equivalen a intersecciones triples, que están asociadas con características espectrales muy complejas (estructuras de línea densas y envolventes espectrales difusas con baja resolución). La transferencia de población entre los estados también es ultrarrápida, tan rápida que la fluorescencia (que procede en una escala de tiempo de nanosegundos) no puede competir. Esto ayuda a entender por qué el catión benceno, como muchos otros cationes radicales orgánicos, no fluoresce.

Sin duda, la reactividad fotoquímica surge cuando la conversión interna hace que el sistema explore el espacio de configuración nuclear de modo que se formen nuevas especies químicas. Existe una gran cantidad de técnicas espectroscópicas de bombeo-sonda de femtosegundos para revelar detalles de estos procesos que ocurren, por ejemplo, en el proceso de la visión.

Problemas de estado sólido

Como lo propuso originalmente Landau ^[35], los electrones libres en un sólido, introducidos por ejemplo mediante dopaje o irradiación, pueden interactuar con las vibraciones de la red para formar una cuasipartícula localizada conocida como polarón . Los polarones fuertemente localizados (también llamados polarones de Holstein) pueden condensarse alrededor de sitios de alta simetría de la red con electrones o huecos que ocupan orbitales degenerados locales que experimentan el JTE. Estos polarones de Jahn-Teller rompen las simetrías de grupo puntual y traslacional de la red donde se encuentran y se les han atribuido papeles importantes en efectos como la magnetorresistencia colosal y la superconductividad .

Las impurezas paramagnéticas en semiconductores , dieléctricos , diamagnéticos y ferromagnéticos pueden describirse utilizando un modelo JT. Por ejemplo, estos modelos se utilizaron ampliamente en los años 1980 y 1990 para describir iones de Cr, V y Ti que sustituyen a Ga en GaAs y GaP.

El fulereno C ₆₀ puede formar compuestos sólidos con metales alcalinos conocidos como fulleruros . Cs ₃ C ₆₀ puede ser superconductor a temperaturas de hasta 38 K bajo presión aplicada, ^[36] mientras que los compuestos de la forma A ₄ C ₆₀ son aislantes (como revisó Gunnarsson ^[37] ). Los efectos JT tanto dentro de las moléculas C ₆₀ (intramoleculares) como entre moléculas C ₆₀ (intermoleculares) juegan un papel en los mecanismos detrás de varias propiedades observadas en estos sistemas. Por ejemplo, podrían significar que el tratamiento de Migdal-Eliashberg de la superconductividad se rompe. Además, los fulleruros pueden formar un llamado nuevo estado de la materia conocido como metal Jahn-Teller, donde los electrones localizados coexisten con metalicidad y persisten las distorsiones JT en las moléculas C _60. ^[38]

Efecto JT cooperativo en cristales

La JTE suele estar asociada a degeneraciones bien localizadas en el espacio, como las que se producen en una molécula pequeña o asociadas a un complejo de metal de transición aislado. Sin embargo, en muchos sistemas periódicos de estado sólido de alta simetría, como las perovskitas, algunos sitios cristalinos permiten la degeneración electrónica dando lugar, en composiciones adecuadas, a redes de centros activos en JT. Esto puede producir una JTE cooperativa, en la que se producen distorsiones globales del cristal debido a degeneraciones locales.

Para determinar la estructura electrónica y geométrica final de un sistema JT cooperativo, es necesario tener en cuenta tanto las distorsiones locales como la interacción entre los diferentes sitios, que tomará la forma necesaria para minimizar la energía global del cristal.

Aunque los trabajos sobre el JTE cooperativo comenzaron a finales de los años cincuenta, ^{[39] [40]} fue en 1960 cuando Kanamori ^[41] publicó el primer trabajo sobre el JTE cooperativo donde se introdujeron muchos elementos importantes presentes en la teoría moderna para este efecto. Esto incluyó el uso de la notación pseudospin para discutir el ordenamiento orbital y discusiones sobre la importancia del JTE para discutir el magnetismo, la competencia de este efecto con el acoplamiento espín-órbita y el acoplamiento de las distorsiones con la tensión de la red. Este punto fue enfatizado posteriormente en la revisión de Gehring y Gehring ^[42] como el elemento clave para establecer un orden de largo alcance entre las distorsiones en la red. Una parte importante de la teoría moderna del JTE cooperativo, ^{[43] puede conducir a} transiciones de fase estructurales .

Se esperaría que muchos sistemas JT cooperativos fueran metales a partir de la teoría de bandas, ya que para producirlos, un orbital degenerado debe llenarse parcialmente y la banda asociada sería metálica. Sin embargo, bajo la perturbación de la distorsión de ruptura de simetría asociada al JTE cooperativo, las degeneraciones en la estructura electrónica se destruyen y el estado fundamental de estos sistemas a menudo resulta ser aislante (ver, por ejemplo, ^[44] ). En muchos casos importantes, como el compuesto original de las colosales perovskitas de magnetorresistencia, LaMnO ₃ , un aumento de la temperatura conduce al desorden en las distorsiones que reduce la división de bandas debido al JTE cooperativo, lo que desencadena una transición metal-aislante.

Efectos relacionados con JT: ordenamiento orbital

En la física moderna del estado sólido, es común clasificar los sistemas según el tipo de grados de libertad que tienen disponibles, como el electrón (metales) o el espín (magnetismo). En los cristales que pueden mostrar el JTE, y antes de que este efecto se produzca mediante distorsiones de ruptura de simetría, se ha descubierto que existe un grado de libertad orbital que consiste en cómo los electrones ocupan los orbitales degenerados locales. Como ya comentaron inicialmente Kugel y Khomskii ^[45] , no todas las configuraciones son equivalentes. La clave es la orientación relativa de estos orbitales ocupados, de la misma manera que la orientación del espín es importante en los sistemas magnéticos, y el estado fundamental solo puede producirse para algún patrón orbital particular. Tanto este patrón como el efecto que da lugar a este fenómeno se denominan habitualmente ordenamiento orbital.

Para predecir el patrón de ordenamiento orbital, Kugel y Khomskii utilizaron una particularización del modelo de Hubbard . En particular, establecieron cómo las interacciones de superintercambio , generalmente descritas por las reglas de Anderson-Kanamori-Goodenough, cambian en presencia de orbitales degenerados. Su modelo, que utiliza una representación de pseudoespín para los orbitales locales, conduce a un modelo similar al de Heisenberg en el que el estado fundamental es una combinación de patrones orbitales y de espín. Utilizando este modelo se puede demostrar, por ejemplo, que el origen del inusual estado ferromagnético aislante fundamental de un sólido como K ₂ CuF ₄ se puede rastrear hasta su ordenamiento orbital.

Incluso cuando se parte de una estructura de simetría relativamente alta, el efecto combinado de las interacciones de intercambio, el acoplamiento espín-órbita, el ordenamiento orbital y las deformaciones cristalinas activadas por la JTE pueden conducir a patrones magnéticos de simetría muy baja con propiedades específicas. Por ejemplo, en CsCuCl ₃ aparece un patrón helicoidal inconmensurable tanto para los orbitales como para las distorsiones a lo largo del eje . Además, muchos de estos compuestos muestran diagramas de fase complejos cuando varía la temperatura o la presión. ${\displaystyle z}$

Referencias

1. Persson, Ingmar (2010). "Iones metálicos hidratados en solución acuosa: ¿Qué tan regulares son sus estructuras?". Química Pura y Aplicada . 82 (10): 1901–1917. doi : 10.1351/PAC-CON-09-10-22 .
2. Shriver, DF; Atkins, PW (1999). Química inorgánica (3.ª ed.). Oxford University Press. págs. 235-236. ISBN 978-0-19-850330-9.
3. Janes, Rob; Moore, Elaine A. (2004). Enlace metal-ligando. Royal Society of Chemistry. ISBN 978-0-85404-979-0.
4. Frank, Patrick; Benfatto, Maurizio; Szilagyi, Robert K.; D'Angelo, Paola; Della Longa, Stefano; Hodgson, Keith O. (2005). "La estructura de la solución de [Cu(aq)] ²⁺ y sus implicaciones para la unión inducida por rack en los sitios activos de la proteína de cobre azul". Química inorgánica . 44 (6): 1922–1933. doi :10.1021/ic0400639. PMID  15762718.
5. Senn, Peter (octubre de 1992). "Un modelo mecánico cuántico simple que ilustra el efecto Jahn-Teller". Journal of Chemical Education . 69 (10): 819. Bibcode :1992JChEd..69..819S. doi :10.1021/ed069p819.
6. Klärner, Frank-Gerrit (2001). "Acerca de la antiaromaticidad del ciclooctatetraeno planar". Angewandte Chemie International Edition en inglés . 40 (21): 3977–3981. doi :10.1002/1521-3773(20011105)40:21<3977::AID-ANIE3977>3.0.CO;2-N.
7. Jahn, HA; Teller, E. (1937). "Estabilidad de moléculas poliatómicas en estados electrónicos degenerados. I. Degeneración orbital". Proc. R. Soc. A . 161 (A905): 220–235. Bibcode :1937RSPSA.161..220J. doi : 10.1098/rspa.1937.0142 .
8. Bersuker, IB (2006). El efecto Jahn-Teller . Cambridge: Cambridge University Press. ISBN 9780521822121.
9. Bates, CA (1978). "Efectos Jahn-Teller en cristales paramagnéticos". Physics Reports . 35 (3): 187–304. Bibcode :1978PhR....35..187B. doi :10.1016/0370-1573(78)90122-9.
10. Englman, R. (1972). El efecto Jahn-Teller en moléculas y cristales . Wiley-Interscience. ISBN 9780471241683.
11. Van Vleck, JH (1939). "Sobre el comportamiento magnético del vanadio, el titanio y el alumbre de cromo". J. Chem. Phys . 7 (1): 61–71. Bibcode :1939JChPh...7...61V. doi :10.1063/1.1750326.
12. Van Vleck, JH (1939). "El efecto Jahn-Teller y la división cristalina brusca para cúmulos de la forma XY6". J. Chem. Phys . 7 (1): 72–84. Bibcode :1939JChPh...7...72V. doi :10.1063/1.1750327.
13. Bleaney, B.; Ingram, DJE (1950). "Resonancia paramagnética en fluosilicato de cobre". Proc. R. Soc. A . 63 (364): 408–409. Bibcode :1950PPSA...63..408B. doi :10.1088/0370-1298/63/4/112.
14. Bleaney, B.; Bowers, KD (1952). "El ion cúprico en un campo eléctrico cristalino trigonal". Proc. R. Soc. A . 65 (392): 667–668. Código Bibliográfico :1952PPSA...65..667B. doi :10.1088/0370-1298/65/8/111.
15. Öpik, U.; Pryce, MHL (1957). "Estudios del efecto Jahn Teller. 1. Un estudio del problema estático". Proc. R. Soc. A . 238 (1215): 425–447. Código Bibliográfico :1957RSPSA.238..425O. doi :10.1098/rspa.1957.0010. S2CID  119862339.
16. Moffitt, W.; Thorson, W. (1957). "Estados vibrónicos de complejos octaédricos". Physical Review . 108 (5): 1251–1255. Código Bibliográfico :1957PhRv..108.1251M. doi :10.1103/PhysRev.108.1251.
17. Moffitt, W.; Liehr, AD (1957). "Inestabilidad configuracional de estados electrónicos degenerados". Physical Review . 106 (6): 1195–1200. Código Bibliográfico :1957PhRv..106.1195M. doi :10.1103/PhysRev.106.1195.
18. Longuet-Higgins, HC; Öpik, U.; Pryce, MHL; Sack, RA (1958). "Estudios del efecto Jahn-Teller. 2. El problema dinámico". Proc. R. Soc. A . 244 (1236): 1–16. Código Bibliográfico :1958RSPSA.244....1L. doi :10.1098/rspa.1958.0022. S2CID  97141844.
19. Bersuker, IB (1963). "Desdoblamiento por inversión de niveles en complejos libres de metales de transición". Sov. Phys. JETP . 16 (4): 933–938. Código Bibliográfico :1963JETP...16..933B.
20. iones d ⁹ coordinados octaédricamente ". Proc. R. Soc. A . 281 (1384): 323–339. Código Bibliográfico :1964RSPSA.281..323O. doi :10.1098/rspa.1964.0185. S2CID  97537997.
21. Ham, FS (1965). "Efecto dinámico de Jahn-Teller en espectros de resonancia paramagnética: factores de reducción orbital y extinción parcial de la interacción espín-órbita" . Physical Review . 138 (6A): A1727–A1740. Bibcode :1965PhRv..138.1727H. doi :10.1103/physrev.138.a1727.
22. Berry, MV (1984). "Factores de fase cuánticos que acompañan a los cambios adiabáticos". Proc. R. Soc. A . 392 (1802): 45–57. Bibcode :1984RSPSA.392...45B. doi :10.1098/rspa.1984.0023. S2CID  46623507.
23. Herzberg, G.; Longuet-Higgins, HC (1963). "Intersección de superficies de energía potencial en moléculas poliatómicas". Discusiones de la Faraday Society . 35 : 77. doi :10.1039/df9633500077.
24. Longuet-Higgins, HC (1975). "Intersección de superficies de energía potencial en moléculas poliatómicas". Proc. R. Soc. A . 344 (1637): 147–156. Código Bibliográfico :1975RSPSA.344..147L. doi :10.1098/rspa.1975.0095. S2CID  98014536.
25. Mead, CA; Truhlar, DG (1979). "Determinación de funciones de onda del movimiento nuclear de Born-Oppenheimer, incluidas las complicaciones debidas a intersecciones cónicas y núcleos idénticos". J. Chem. Phys . 70 (5): 2284–2296. Código Bibliográfico :1979JChPh..70.2284M. doi :10.1063/1.437734.
26. Kroto, HW; Heath, JR; O'Brien, SC; Curl, RF; Smalley, RE (1985). "C ₆₀ – Buckminsterfullereno". Nature . 318 (6042): 162–163. Código Bibliográfico :1985Natur.318..162K. doi :10.1038/318162a0. S2CID  4314237.
27. Chancey, CC; O'Brien, MC M (1997). El efecto Jahn-Teller en C ₆₀ y otros complejos icosaédricos . Princeton: Princeton University Press. ISBN 9780691044453.
28. Bednorz, JG; Müller, KA (1986). "Posible superconductividad de alta temperatura _en el sistema BaLaCuO". Z. Phys. B . 64 (2): 189–193. Código Bibliográfico :1986ZPhyB..64..189B. doi :10.1007/bf01303701. S2CID  118314311.
29. Millis, AJ; Shraiman, BI; Müller, R. (1996). "Efecto dinámico de Jahn-Teller y magnetorresistencia colosal en La _1−x Sr _x MnO ₃ ". Phys. Rev. Lett . 77 (1): 175–178. arXiv : cond-mat/9507084 . Código Bibliográfico :1996PhRvL..77..175M. doi :10.1103/PhysRevLett.77.175. PMID  10061800. S2CID  8623731.
30. Liehr, AD (1963). "Aspectos topológicos del problema de estabilidad conformacional .1. Estados electrónicos degenerados". J. Phys. Chem . 67 (2): 389–+. doi :10.1021/j100796a043.
31. Ham, FS (1968). "Efecto del acoplamiento lineal de Jahn-Teller sobre la resonancia paramagnética en un estado ^{2 E".} Physical Review . 166 (2): 307–321. Código Bibliográfico :1968PhRv..166..307H. doi :10.1103/PhysRev.166.307.
32. Yates, JH; Pitzer, RM (1979). "Estructuras moleculares y electrónicas de trifluoruros de metales de transición". J. Chem. Phys . 70 (9): 4049–4055. Código Bibliográfico :1979JChPh..70.4049Y. doi :10.1063/1.438027.
33. Ridente, Enrico; Hait, Diptarka; Haugen, Eric A.; Ross, Andrew D.; Neumark, Daniel M.; Head-Gordon, Martin; Leone, Stephen R. (19 de mayo de 2023). "Ruptura de simetría de femtosegundos y relajación coherente de cationes de metano mediante espectroscopia de rayos X". Science . 380 (6646): 713–717. arXiv : 2212.12875 . doi :10.1126/science.adg4421. ISSN  0036-8075. PMID  37141314.
34. Deeth, RJ; Hitchman, MA (1985). "Factores que influyen en las distorsiones de Jahn-Teller en complejos de cobre(II) de seis coordenadas y de níquel(II) de bajo espín". Inorg. Chem . 25 (8): 1225–1233. doi :10.1021/ic00228a031.
35. Landau, LD (1933). "Über die Bewegung der Elektronen en Kristallgitter". Física. Z. Sowjetunion . 3 : 644–645.
36. Ganin, A. Y; Takabayashi, Y.; Khimyak, YZ; Margadonna, S.; Tamai, A.; Rosseinsky, M. J; Prassides, K. (2008). "Superconductividad a granel a 38 K en un sistema molecular". Nat. Mater . 7 (5): 367–71. Bibcode :2008NatMa...7..367G. doi :10.1038/nmat2179. PMID  18425134.
37. Gunnarsson, O. (1997). "Superconductividad en fulleruros". Rev. Mod. Phys . 69 (2): 575–606. arXiv : cond-mat/9611150 . Código Bibliográfico :1997RvMP...69..575G. doi :10.1103/RevModPhys.69.575. S2CID  18025631.
38. Zadik, Ruth H.; Takabayashi, Yasuhiro; Klupp, Gyöngyi; Colman, Ross H.; Ganin, Alexey Y.; Potočnik, Anton; Jeglič, Peter; Arčon, Denis; Matus, Peter; Kamarás, Katalin; Kasahara, Yuichi; Iwasa, Yoshihiro; Fitch, Andrew N.; Ohishi, Yasuo; Garbarino, Gastón; Kato, Kenichi; Rosseinsky, Mateo J.; Prassides, Kosmas (2015). "Superconductividad no convencional optimizada en un metal molecular de Jahn-Teller". Ciencia. Avanzado . 1 (3): 500059. Código bibliográfico : 2015SciA....1E0059Z. doi :10.1126/sciadv.1500059. Número de modelo : PMID 26601168  . 
39. Dunitz, JD; Orgel, LE (1957). "Propiedades electrónicas de óxidos de metales de transición—I: Distorsiones de la simetría cúbica". J. Phys. Chem. Solids . 3 (1): 20–29. Bibcode :1957JPCS....3...20D. doi :10.1016/0022-3697(57)90043-4.
40. McClure, DS (1957). "La distribución de cationes de metales de transición en espinelas". J. Phys. Chem. Solids . 3 (3–4): 311–317. Bibcode :1957JPCS....3..311M. doi :10.1016/0022-3697(57)90034-3.
41. Kanamori, J. (1960). "Distorsión cristalina en compuestos magnéticos". J. Appl. Phys . 31 (5): S14–S23. Código Bibliográfico :1960JAP....31S..14K. doi :10.1063/1.1984590.
42. Gehring, GA; Gehring, KA (1975). "Efectos cooperativos de Jahn-Teller". Rep. Prog. Phys . 38 (1): 1. Bibcode :1975RPPh...38....1G. doi :10.1088/0034-4885/38/1/001. S2CID  250892454.
43. Kaplan, MD; Vekhter, BG (1995). Fenómenos cooperativos en cristales de Jahn-Teller . Nueva York: Plenum Press. ISBN 978-1-4615-1859-4.
44. Lee, JH; Delaney, KT; Bousquet, E.; Spaldin, NA; Rabe, KM (2013). "Fuerte acoplamiento de la distorsión de Jahn-Teller a la rotación del octaedro de oxígeno y propiedades funcionales en LaMnO ₃ ortorrómbico deformado epitaxialmente ". Phys. Rev. B . 88 (17): 174426. arXiv : 1307.3347 . Bibcode :2013PhRvB..88q4426L. doi :10.1103/PhysRevB.88.174426. S2CID  53333115.
45. Kugel, KI; Khomskii, DI (1982). "Efecto Jahn-Teller y magnetismo: compuestos de metales de transición". Sov. Phys. Usp . 25 (4): 231–256. doi : 10.3367/UFNr.0136.198204c.0621 .

Enlaces externos

• Una serie de simposios internacionales (en su mayoría bianuales) tratan problemas actuales y desarrollos modernos en el campo, siendo los más recientes de ellos
  • JT2012, Tsukuba, Japón
  • JT2014, Graz, Austria
  • JT2016, Tartu Estonia Archivado el 2 de febrero de 2017 en Wayback Machine.

Las conferencias están supervisadas y guiadas por el comité directivo internacional de JT.

• Aquí se ilustra la diferencia entre la rotación real y la pseudorotación de una molécula de fulereno.