Operador discreto de Laplace

Análogo del operador continuo de Laplace

En matemáticas , el operador de Laplace discreto es un análogo del operador de Laplace continuo , definido de modo que tenga significado en un gráfico o una cuadrícula discreta . Para el caso de un gráfico de dimensión finita (que tiene un número finito de aristas y vértices), el operador de Laplace discreto se denomina más comúnmente matriz laplaciana .

El operador de Laplace discreto aparece en problemas de física como el modelo de Ising y la gravedad cuántica de bucles , así como en el estudio de sistemas dinámicos discretos . También se utiliza en análisis numérico como sustituto del operador de Laplace continuo. Las aplicaciones comunes incluyen el procesamiento de imágenes , ^[1] donde se lo conoce como filtro de Laplace , y en el aprendizaje automático para la agrupación y el aprendizaje semisupervisado en gráficos de vecindad.

Definiciones

Gráficas laplacianas

Existen varias definiciones del laplaciano discreto para grafos , que difieren en el signo y el factor de escala (a veces se promedia sobre los vértices vecinos, otras veces simplemente se suma; esto no hace ninguna diferencia para un grafo regular ). La definición tradicional del laplaciano de grafos, que se da a continuación, corresponde al laplaciano continuo negativo en un dominio con un borde libre.

Sea un grafo con vértices y aristas . Sea una función de los vértices que toman valores en un anillo . Entonces, el laplaciano discreto que actúa sobre se define por ${\displaystyle G=(V,E)}$ ${\displaystyle V}$ ${\displaystyle E}$ ${\displaystyle \phi \colon V\to R}$ ${\displaystyle \Delta }$ ${\displaystyle \phi }$

${\displaystyle (\Delta \phi )(v)=\sum _{w:\,d(w,v)=1}\left[\phi (v)-\phi (w)\right]}$

donde es la distancia gráfica entre los vértices w y v. Por lo tanto, esta suma se aplica a los vecinos más próximos del vértice v . Para un grafo con un número finito de aristas y vértices, esta definición es idéntica a la de la matriz laplaciana . Es decir, se puede escribir como un vector columna; y también lo es el producto del vector columna y la matriz laplaciana, mientras que es simplemente la v' ésima entrada del vector producto. ${\displaystyle d(w,v)}$ ${\displaystyle \phi }$ ${\displaystyle \Delta \phi }$ ${\displaystyle (\Delta \phi )(v)}$

Si el gráfico tiene aristas ponderadas, es decir, se da una función de ponderación, entonces la definición se puede generalizar a ${\displaystyle \gamma \colon E\to R}$

${\displaystyle (\Delta _{\gamma }\phi )(v)=\sum _{w:\,d(w,v)=1}\gamma _{wv}\left[\phi (v)-\phi (w)\right]}$

¿Dónde está el valor del peso en el borde ? ${\displaystyle \gamma _{wv}}$ ${\displaystyle wv\in E}$

Estrechamente relacionado con el laplaciano discreto está el operador de promedio :

${\displaystyle (M\phi )(v)={\frac {1}{\deg v}}\sum _{w:\,d(w,v)=1}\phi (w).}$

Laplacianos de malla

Además de considerar la conectividad de nodos y aristas en un grafo, los operadores de Laplace de malla tienen en cuenta la geometría de una superficie (por ejemplo, los ángulos en los nodos). Para una malla de triángulos de variedades bidimensionales, el operador de Laplace-Beltrami de una función escalar en un vértice se puede aproximar como ${\displaystyle u}$ ${\displaystyle i}$

${\displaystyle (\Delta u)_{i}\equiv {\frac {1}{2A_{i}}}\sum _{j}(\cot \alpha _{ij}+\cot \beta _{ij})(u_{j}-u_{i}),}$

donde la suma es sobre todos los vértices adyacentes de , y son los dos ángulos opuestos del borde , y es el área del vértice de ; es decir, p. ej. un tercio de las áreas sumadas de los triángulos incidentes a . Es importante notar que el signo del operador discreto de Laplace-Beltrami es convencionalmente opuesto al signo del operador de Laplace ordinario . La fórmula de cotangente anterior se puede derivar usando muchos métodos diferentes entre los que se encuentran elementos finitos lineales por partes , volúmenes finitos y cálculo exterior discreto ^[2] (descarga PDF: [1]). ${\displaystyle j}$ ${\displaystyle i}$ ${\displaystyle \alpha _{ij}}$ ${\displaystyle \beta _{ij}}$ ${\displaystyle ij}$ ${\displaystyle A_{i}}$ ${\displaystyle i}$ ${\displaystyle i}$

Para facilitar el cálculo, el laplaciano se codifica en una matriz tal que . Sea la matriz cotangente (dispersa) con entradas ${\displaystyle L\in \mathbb {R} ^{|V|\times |V|}}$ ${\displaystyle Lu=(\Delta u)_{i}}$ ${\displaystyle C}$

${\displaystyle C_{ij}={\begin{cases}{\frac {1}{2}}(\cot \alpha _{ij}+\cot \beta _{ij})&ij{\text{ is an edge, that is }}j\in N(i),\\-\sum \limits _{k\in N(i)}C_{ik}&i=j,\\0&{\text{otherwise}}\end{cases}}}$

donde denota la vecindad de , y sea la matriz de masa diagonal cuya entrada -ésima a lo largo de la diagonal es el área del vértice . Entonces es la discretización buscada del laplaciano. ${\displaystyle N(i)}$ ${\displaystyle i}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle i}$ ${\displaystyle A_{i}}$ ${\displaystyle L=M^{-1}C}$

^{En [3]} se ofrece una descripción más general de los operadores de malla.

Diferencias finitas

Las aproximaciones del laplaciano obtenidas por el método de diferencias finitas o por el método de elementos finitos también se pueden llamar laplacianos discretos . Por ejemplo, el laplaciano en dos dimensiones se puede aproximar utilizando el método de diferencias finitas de plantilla de cinco puntos , lo que da como resultado

${\displaystyle \Delta f(x,y)\approx {\frac {f(x-h,y)+f(x+h,y)+f(x,y-h)+f(x,y+h)-4f(x,y)}{h^{2}}},}$

donde el tamaño de la cuadrícula es h en ambas dimensiones, de modo que la plantilla de cinco puntos de un punto ( x ,  y ) en la cuadrícula es

${\displaystyle \{(x-h,y),(x,y),(x+h,y),(x,y-h),(x,y+h)\}.}$

Si el tamaño de la cuadrícula h = 1, el resultado es el Laplaciano discreto negativo en el grafo, que es la cuadrícula de red cuadrada . Aquí no hay restricciones sobre los valores de la función f ( x , y ) en el límite de la cuadrícula de red, por lo tanto, este es el caso de que no hay fuente en el límite, es decir, una condición de límite sin flujo (también conocida como condición de límite de aislamiento o condición de límite de Neumann homogénea ). El control de la variable de estado en el límite, como f ( x , y ) dada en el límite de la cuadrícula (también conocida como condición de límite de Dirichlet ), rara vez se usa para los Laplacianos de grafos, pero es común en otras aplicaciones.

Los laplacianos discretos multidimensionales en cuadrículas regulares de cuboide rectangular ^{[ ancla rota ]} tienen propiedades muy especiales, por ejemplo, son sumas de Kronecker de laplacianos discretos unidimensionales, véase suma de Kronecker de laplacianos discretos , en cuyo caso todos sus valores y vectores propios se pueden calcular explícitamente.

Método de elementos finitos

En este enfoque, el dominio se discretiza en elementos más pequeños, a menudo triángulos o tetraedros, pero también son posibles otros elementos como rectángulos o cuboides. Luego, el espacio de soluciones se aproxima utilizando las llamadas funciones de forma de un grado predefinido. Luego, la ecuación diferencial que contiene el operador de Laplace se transforma en una formulación variacional y se construye un sistema de ecuaciones (problemas lineales o de valores propios). Las matrices resultantes suelen ser muy dispersas y se pueden resolver con métodos iterativos.

Procesamiento de imágenes

El operador de Laplace discreto se utiliza a menudo en el procesamiento de imágenes, por ejemplo, en aplicaciones de detección de bordes y estimación de movimiento. ^[4] El laplaciano discreto se define como la suma de las derivadas segundas Operador de Laplace#Expresiones de coordenadas y se calcula como la suma de las diferencias sobre los vecinos más cercanos del píxel central. Dado que los filtros de derivadas suelen ser sensibles al ruido en una imagen, el operador de Laplace suele ir precedido de un filtro de suavizado (como un filtro gaussiano) para eliminar el ruido antes de calcular la derivada. El filtro de suavizado y el filtro de Laplace suelen combinarse en un único filtro. ^[5]

Implementación mediante discretización de operadores

Para señales unidimensionales, bidimensionales y tridimensionales, el laplaciano discreto se puede dar como convolución con los siguientes núcleos:

Filtro 1D: , ${\displaystyle {\vec {D}}_{x}^{2}={\begin{bmatrix}1&-2&1\end{bmatrix}}}$

Filtro 2D: . ${\displaystyle \mathbf {D} _{xy}^{2}={\begin{bmatrix}0&1&0\\1&-4&1\\0&1&0\end{bmatrix}}}$

${\displaystyle \mathbf {D} _{xy}^{2}}$corresponde a la fórmula de diferencias finitas ( plantilla de cinco puntos ) vista anteriormente. Es estable para campos que varían muy suavemente, pero para ecuaciones con soluciones que varían rápidamente se requiere una forma más estable e isótropa del operador laplaciano, ^[6] como la plantilla de nueve puntos , que incluye las diagonales:

Filtro 2D: , ${\displaystyle \mathbf {D} _{xy}^{2}={\begin{bmatrix}0.25&0.5&0.25\\0.5&-3&0.5\\0.25&0.5&0.25\end{bmatrix}}}$

Filtro 3D: el uso de una plantilla de siete puntos viene dado por: ${\displaystyle \mathbf {D} _{xyz}^{2}}$

primer plano = ; segundo plano = ; tercer plano = . ${\displaystyle {\begin{bmatrix}0&0&0\\0&1&0\\0&0&0\end{bmatrix}}}$ ${\displaystyle {\begin{bmatrix}0&1&0\\1&-6&1\\0&1&0\end{bmatrix}}}$ ${\displaystyle {\begin{bmatrix}0&0&0\\0&1&0\\0&0&0\end{bmatrix}}}$

y utilizando una plantilla de 27 puntos por: ^[7]

primer plano = ; segundo plano = ; tercer plano = . ${\displaystyle {\frac {1}{26}}{\begin{bmatrix}2&3&2\\3&6&3\\2&3&2\end{bmatrix}}}$ ${\displaystyle {\frac {1}{26}}{\begin{bmatrix}3&6&3\\6&-88&6\\3&6&3\end{bmatrix}}}$ ${\displaystyle {\frac {1}{26}}{\begin{bmatrix}2&3&2\\3&6&3\\2&3&2\end{bmatrix}}}$

Filtro n D : Para el elementodel núcleo ${\displaystyle a_{x_{1},x_{2},\dots ,x_{n}}}$ ${\displaystyle \mathbf {D} _{x_{1},x_{2},\dots ,x_{n}}^{2},}$

${\displaystyle a_{x_{1},x_{2},\dots ,x_{n}}=\left\{{\begin{array}{ll}-2n&{\text{if }}s=n,\\1&{\text{if }}s=n-1,\\0&{\text{otherwise,}}\end{array}}\right.}$

donde x _i es la posición ( −1 , 0 o 1 ) del elemento en el núcleo en la dirección i -ésima, y ​​s es el número de direcciones i para las que x _i = 0 .

Tenga en cuenta que la versión n D, que se basa en la generalización gráfica del Laplaciano, supone que todos los vecinos están a la misma distancia y, por lo tanto, conduce al siguiente filtro 2D con diagonales incluidas, en lugar de la versión anterior:

Filtro 2D: ${\displaystyle \mathbf {D} _{xy}^{2}={\begin{bmatrix}1&1&1\\1&-8&1\\1&1&1\end{bmatrix}}.}$

Estos núcleos se deducen utilizando cocientes diferenciales discretos.

Se puede demostrar ^{[8] [9]} que la siguiente aproximación discreta del operador laplaciano bidimensional como una combinación convexa de operadores de diferencia

${\displaystyle \nabla _{\gamma }^{2}=(1-\gamma )\nabla _{5}^{2}+\gamma \nabla _{\times }^{2}=(1-\gamma ){\begin{bmatrix}0&1&0\\1&-4&1\\0&1&0\end{bmatrix}}+\gamma {\begin{bmatrix}1/2&0&1/2\\0&-2&0\\1/2&0&1/2\end{bmatrix}}}$

para γ ∈ [0, 1] es compatible con propiedades de escala espacial discreta, donde específicamente el valor γ = 1/3 da la mejor aproximación de simetría rotacional. ^{[8] [9] [10]} Con respecto a las señales tridimensionales, se muestra ^[9] que el operador laplaciano puede aproximarse mediante la familia de dos parámetros de operadores de diferencia.

${\displaystyle \nabla _{\gamma _{1},\gamma _{2}}^{2}=(1-\gamma _{1}-\gamma _{2})\,\nabla _{7}^{2}+\gamma _{1}\,\nabla _{+^{3}}^{2}+\gamma _{2}\,\nabla _{\times ^{3}}^{2}),}$

dónde

${\displaystyle (\nabla _{7}^{2}f)_{0,0,0}=f_{-1,0,0}+f_{+1,0,0}+f_{0,-1,0}+f_{0,+1,0}+f_{0,0,-1}+f_{0,0,+1}-6f_{0,0,0},}$

${\displaystyle (\nabla _{+^{3}}^{2}f)_{0,0,0}={\frac {1}{4}}(f_{-1,-1,0}+f_{-1,+1,0}+f_{+1,-1,0}+f_{+1,+1,0}+f_{-1,0,-1}+f_{-1,0,+1}+f_{+1,0,-1}+f_{+1,0,+1}+f_{0,-1,-1}+f_{0,-1,+1}+f_{0,+1,-1}+f_{0,+1,+1}-12f_{0,0,0}),}$

${\displaystyle (\nabla _{\times ^{3}}^{2}f)_{0,0,0}={\frac {1}{4}}(f_{-1,-1,-1}+f_{-1,-1,+1}+f_{-1,+1,-1}+f_{-1,+1,+1}+f_{+1,-1,-1}+f_{+1,-1,+1}+f_{+1,+1,-1}+f_{+1,+1,+1}-8f_{0,0,0}).}$

Implementación mediante reconstrucción continua

Una señal discreta, que comprende imágenes, puede considerarse como una representación discreta de una función continua , donde el vector de coordenadas y el dominio de valores son reales . Por lo tanto, la operación de derivación es directamente aplicable a la función continua, . En particular, cualquier imagen discreta, con presunciones razonables sobre el proceso de discretización, por ejemplo, suponiendo funciones limitadas por bandas o funciones expandibles por ondículas, etc., puede reconstruirse por medio de funciones de interpolación de buen comportamiento subyacentes a la formulación de reconstrucción, ^[11] ${\displaystyle f({\bar {r}})}$ ${\displaystyle {\bar {r}}\in R^{n}}$ ${\displaystyle f\in R}$ ${\displaystyle f}$

${\displaystyle f({\bar {r}})=\sum _{k\in K}f_{k}\mu _{k}({\bar {r}})}$

donde son representaciones discretas de en una cuadrícula y son funciones de interpolación específicas de la cuadrícula . En una cuadrícula uniforme, como imágenes, y para funciones limitadas por bandas, las funciones de interpolación son invariantes al desplazamiento, lo que equivale a que es una función sinc adecuadamente dilatada definida en dimensiones, es decir . Otras aproximaciones de en cuadrículas uniformes, son funciones gaussianas adecuadamente dilatadas en dimensiones. En consecuencia, el laplaciano discreto se convierte en una versión discreta del laplaciano del continuo ${\displaystyle f_{k}\in R}$ ${\displaystyle f}$ ${\displaystyle K}$ ${\displaystyle \mu _{k}}$ ${\displaystyle K}$ ${\displaystyle \mu _{k}({\bar {r}})=\mu ({\bar {r}}-{\bar {r}}_{k})}$ ${\displaystyle \mu }$ ${\displaystyle n}$ ${\displaystyle {\bar {r}}=(x_{1},x_{2}...x_{n})^{T}}$ ${\displaystyle \mu }$ ${\displaystyle n}$ ${\displaystyle f({\bar {r}})}$

${\displaystyle \nabla ^{2}f({\bar {r}}_{k})=\sum _{k'\in K}f_{k'}(\nabla ^{2}\mu ({\bar {r}}-{\bar {r}}_{k'}))|_{{\bar {r}}={\bar {r}}_{k}}}$

que a su vez es una convolución con el Laplaciano de la función de interpolación en la cuadrícula uniforme (imagen) . Una ventaja de usar gaussianos como funciones de interpolación es que producen operadores lineales, incluidos los laplacianos, que están libres de artefactos rotacionales del marco de coordenadas en el que se representa mediante , en dimensiones, y son conscientes de la frecuencia por definición. Un operador lineal no solo tiene un rango limitado en el dominio sino también un rango efectivo en el dominio de frecuencia (alternativamente espacio de escala gaussiana) que se puede controlar explícitamente a través de la varianza del gaussiano de una manera basada en principios. El filtrado resultante se puede implementar mediante filtros separables y representaciones de diezmado (procesamiento de señales) / piramidales (procesamiento de imágenes) para una mayor eficiencia computacional en dimensiones. En otras palabras, el filtro laplaciano discreto de cualquier tamaño se puede generar convenientemente como el laplaciano muestreado de Gaussiano con un tamaño espacial adecuado a las necesidades de una aplicación particular controlada por su varianza. Los monomios que son operadores no lineales también se pueden implementar utilizando un enfoque de reconstrucción y aproximación similar, siempre que la señal esté suficientemente sobremuestreada. De este modo, se pueden implementar operadores no lineales como, por ejemplo, el tensor de estructura y el tensor de estructura generalizado , que se utilizan en el reconocimiento de patrones por su optimalidad total de mínimos cuadrados en la estimación de la orientación. ${\displaystyle K}$ ${\displaystyle f}$ ${\displaystyle f_{k}}$ ${\displaystyle n}$ ${\displaystyle {\bar {r}}}$ ${\displaystyle n}$

Espectro

El espectro del laplaciano discreto en una cuadrícula infinita es de interés clave; dado que es un operador autoadjunto , tiene un espectro real. Para la convención sobre , el espectro se encuentra dentro de (ya que el operador de promediación tiene valores espectrales en ). Esto también se puede ver aplicando la transformada de Fourier. Nótese que el laplaciano discreto en una cuadrícula infinita tiene un espectro absolutamente continuo y, por lo tanto, no tiene valores propios ni funciones propias. ${\displaystyle \Delta =I-M}$ ${\displaystyle Z}$ ${\displaystyle [0,2]}$ ${\displaystyle [-1,1]}$

Teoremas

Si el gráfico es una cuadrícula infinita de cuadrículas , entonces se puede demostrar que esta definición del laplaciano corresponde al laplaciano continuo en el límite de una cuadrícula infinitamente fina. Así, por ejemplo, en una cuadrícula unidimensional tenemos

${\displaystyle {\frac {\partial ^{2}F}{\partial x^{2}}}=\lim _{\epsilon \rightarrow 0}{\frac {[F(x+\epsilon )-F(x)]-[F(x)-F(x-\epsilon )]}{\epsilon ^{2}}}.}$

Esta definición del laplaciano se utiliza habitualmente en análisis numérico y en procesamiento de imágenes . En el procesamiento de imágenes, se considera un tipo de filtro digital , más concretamente un filtro de borde , denominado filtro de Laplace .

Ecuación de calor discreta

Supongamos que describe una distribución de temperatura a lo largo de un gráfico , donde es la temperatura en el vértice . Según la ley de enfriamiento de Newton , el calor transferido de un nodo a otro es proporcional a si los nodos y están conectados (si no están conectados, no se transfiere calor). Entonces, para la conductividad térmica , ${\textstyle \phi }$ ${\textstyle \phi _{i}}$ ${\textstyle i}$ ${\textstyle i}$ ${\textstyle j}$ ${\textstyle \phi _{i}-\phi _{j}}$ ${\textstyle i}$ ${\textstyle j}$ ${\textstyle k}$

${\displaystyle {\begin{aligned}{\frac {d\phi _{i}}{dt}}&=-k\sum _{j}A_{ij}\left(\phi _{i}-\phi _{j}\right)\\&=-k\left(\phi _{i}\sum _{j}A_{ij}-\sum _{j}A_{ij}\phi _{j}\right)\\&=-k\left(\phi _{i}\ \deg(v_{i})-\sum _{j}A_{ij}\phi _{j}\right)\\&=-k\sum _{j}\left(\delta _{ij}\ \deg(v_{i})-A_{ij}\right)\phi _{j}\\&=-k\sum _{j}\left(L_{ij}\right)\phi _{j}.\end{aligned}}}$

En notación matricial-vectorial,

${\displaystyle {\begin{aligned}{\frac {d\phi }{dt}}&=-k(D-A)\phi \\&=-kL\phi ,\end{aligned}}}$

Lo cual da

${\displaystyle {\frac {d\phi }{dt}}+kL\phi =0.}$

Nótese que esta ecuación toma la misma forma que la ecuación de calor , donde la matriz − L reemplaza al operador laplaciano ; de ahí el nombre de "grafo laplaciano". ${\textstyle \nabla ^{2}}$

Para encontrar una solución a esta ecuación diferencial, aplique técnicas estándar para resolver una ecuación diferencial matricial de primer orden . Es decir, escríbala como una combinación lineal de vectores propios de L (de modo que ) con coeficientes dependientes del tiempo, ${\textstyle \phi }$ ${\textstyle \mathbf {v} _{i}}$ ${\textstyle L\mathbf {v} _{i}=\lambda _{i}\mathbf {v} _{i}}$ ${\textstyle \phi (t)=\sum _{i}c_{i}(t)\mathbf {v} _{i}.}$

Conectando a la expresión original (dado que L es una matriz simétrica, sus vectores propios de norma unitaria son ortogonales): ${\textstyle \mathbf {v} _{i}}$

${\displaystyle {\begin{aligned}0={}&{\frac {d\left(\sum _{i}c_{i}(t)\mathbf {v} _{i}\right)}{dt}}+kL\left(\sum _{i}c_{i}(t)\mathbf {v} _{i}\right)\\{}={}&\sum _{i}\left[{\frac {dc_{i}(t)}{dt}}\mathbf {v} _{i}+kc_{i}(t)L\mathbf {v} _{i}\right]\\{}={}&\sum _{i}\left[{\frac {dc_{i}(t)}{dt}}\mathbf {v} _{i}+kc_{i}(t)\lambda _{i}\mathbf {v} _{i}\right]\\\Rightarrow 0={}&{\frac {dc_{i}(t)}{dt}}+k\lambda _{i}c_{i}(t),\\\end{aligned}}}$

cuya solución es

${\displaystyle c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}.}$

Como se ha demostrado anteriormente, los valores propios de L no son negativos, lo que demuestra que la solución de la ecuación de difusión se acerca al equilibrio, porque solo decae exponencialmente o permanece constante. Esto también demuestra que, dada la condición inicial , se puede encontrar la solución en cualquier momento t . ^[12] ${\textstyle \lambda _{i}}$ ${\textstyle \lambda _{i}}$ ${\textstyle c_{i}(0)}$

Para encontrar cada uno en términos de la condición inicial general , simplemente proyecte sobre los vectores propios de la norma unitaria ; ${\textstyle c_{i}(0)}$ ${\textstyle i}$ ${\textstyle \phi (0)}$ ${\textstyle \phi (0)}$ ${\textstyle \mathbf {v} _{i}}$

${\displaystyle c_{i}(0)=\left\langle \phi (0),\mathbf {v} _{i}\right\rangle }$.

Este enfoque se ha aplicado al modelado cuantitativo de transferencia de calor en redes no estructuradas. ^{[13] [14]}

En el caso de grafos no dirigidos, esto funciona porque es simétrico y, según el teorema espectral , sus vectores propios son todos ortogonales. Por lo tanto, la proyección sobre los vectores propios de es simplemente una transformación de coordenadas ortogonales de la condición inicial a un conjunto de coordenadas que decaen exponencialmente e independientemente unas de otras. ${\textstyle L}$ ${\textstyle L}$

Comportamiento de equilibrio

Para entenderlo , los únicos términos que quedan son aquellos donde , ya que ${\textstyle \lim _{t\to \infty }\phi (t)}$ ${\textstyle c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}}$ ${\textstyle \lambda _{i}=0}$

${\displaystyle \lim _{t\to \infty }e^{-k\lambda _{i}t}={\begin{cases}0,&{\text{if}}&\lambda _{i}>0\\1,&{\text{if}}&\lambda _{i}=0\end{cases}}}$

En otras palabras, el estado de equilibrio del sistema está determinado completamente por el núcleo de . ${\textstyle L}$

Dado que, por definición , el vector de todos los unos está en el núcleo, si hay componentes conexos disjuntos en el grafo, entonces este vector de todos los unos se puede dividir en la suma de vectores propios independientes de unos y ceros, donde cada componente conexo corresponde a un vector propio con unos en los elementos del componente conexo y ceros en el resto. ${\textstyle \sum _{j}L_{ij}=0}$ ${\textstyle \mathbf {v} ^{1}}$ ${\textstyle k}$ ${\textstyle k}$ ${\textstyle \lambda =0}$

La consecuencia de esto es que para una condición inicial dada para un gráfico con vértices ${\textstyle c(0)}$ ${\textstyle N}$

${\displaystyle \lim _{t\to \infty }\phi (t)=\left\langle c(0),\mathbf {v^{1}} \right\rangle \mathbf {v^{1}} }$

dónde

${\displaystyle \mathbf {v^{1}} ={\frac {1}{\sqrt {N}}}[1,1,\ldots ,1]}$

Para cada elemento de , es decir, para cada vértice del gráfico, se puede reescribir como ${\textstyle \phi _{j}}$ ${\textstyle \phi }$ ${\textstyle j}$

${\displaystyle \lim _{t\to \infty }\phi _{j}(t)={\frac {1}{N}}\sum _{i=1}^{N}c_{i}(0)}$.

En otras palabras, en estado estacionario, el valor de converge al mismo valor en cada uno de los vértices del gráfico, que es el promedio de los valores iniciales en todos los vértices. Dado que esta es la solución de la ecuación de difusión del calor, esto tiene mucho sentido intuitivamente. Esperamos que los elementos vecinos en el gráfico intercambien energía hasta que esa energía se distribuya uniformemente entre todos los elementos que están conectados entre sí. ${\textstyle \phi }$

Ejemplo del operador en una cuadrícula

Este GIF muestra la progresión de la difusión, resuelta mediante la técnica del laplaciano de grafos. Se construye un grafo sobre una cuadrícula, donde cada píxel del grafo está conectado a los 8 píxeles que lo rodean. Los valores de la imagen se difunden luego suavemente hacia sus vecinos a lo largo del tiempo a través de estas conexiones. Esta imagen en particular comienza con tres valores puntuales fuertes que se transmiten lentamente a sus vecinos. Todo el sistema finalmente se estabiliza en el mismo valor en el equilibrio.

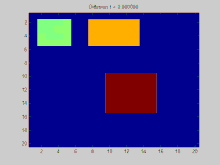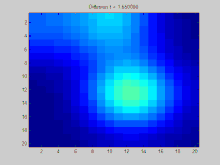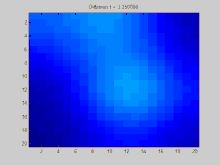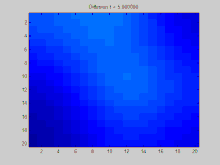
En esta sección se muestra un ejemplo de una función que se difunde a lo largo del tiempo a través de un gráfico. El gráfico de este ejemplo se construye en una cuadrícula discreta en 2D, con puntos de la cuadrícula conectados a sus ocho vecinos. Se especifica que tres puntos iniciales tienen un valor positivo, mientras que el resto de los valores de la cuadrícula son cero. Con el tiempo, la desintegración exponencial actúa para distribuir los valores en estos puntos de manera uniforme a lo largo de toda la cuadrícula. ${\textstyle \phi }$

A continuación se incluye el código fuente completo de Matlab que se utilizó para generar esta animación. Muestra el proceso de especificación de las condiciones iniciales, la proyección de estas condiciones iniciales sobre los valores propios de la matriz laplaciana y la simulación de la desintegración exponencial de estas condiciones iniciales proyectadas.

N = 20 ; % El número de píxeles a lo largo de una dimensión de la imagen A = ceros ( N , N ); % La imagen Adj = ceros ( N * N , N * N ); % La matriz de adyacencia               % Use 8 vecinos y complete la matriz de adyacencia dx = [ - 1 , 0 , 1 , - 1 , 1 , - 1 , 0 , 1 ]; dy = [ - 1 , - 1 , - 1 , 0 , 0 , 1 , 1 , 1 ]; para x = 1 : N para y = 1 : N índice = ( x - 1 ) * N + y ; para ne = 1 : longitud ( dx ) newx = x + dx ( ne ); newy = y + dy ( ne ); si newx > 0 && newx <= N && newy > 0 && newy <= N índice2 = ( newx - 1 ) * N + newy ; Adj ( índice , índice2 ) = 1 ; fin fin fin fin                                                                                      % A CONTINUACIÓN SE PRESENTA EL CÓDIGO CLAVE QUE CALCULA LA SOLUCIÓN DE LA ECUACIÓN DIFERENCIAL Deg = diag ( sum ( Adj , 2 )); % Calcular la matriz de grados L = Deg - Adj ; % Calcular la matriz laplaciana en términos de las matrices de grados y adyacencia [ V , D ] = eig ( L ); % Calcular los valores propios/vectores de la matriz laplaciana D = diag ( D );               % Condición inicial (coloque algunos valores positivos grandes alrededor y % haga que todo lo demás sea cero) C0 = ceros ( N , N ); C0 ( 2 : 5 , 2 : 5 ) = 5 ; C0 ( 10 : 15 , 10 : 15 ) = 10 ; C0 ( 2 : 5 , 8 : 13 ) = 7 ; C0 = C0 (:);              C0V = V '* C0 ; % Transforma la condición inicial en el sistema de coordenadas % de los vectores propios para t = 0 : 0.05 : 5 % Recorre los tiempos y decae cada componente inicial Phi = C0V .* exp ( - D * t ); % Decaimiento exponencial para cada componente Phi = V * Phi ; % Transforma del sistema de coordenadas del vector propio al sistema de coordenadas original Phi = reshape ( Phi , N , N ); % Muestra los resultados y los escribe en un archivo GIF imagesc ( Phi ); caxis ([ 0 , 10 ]); title ( sprintf ( 'Diffusion t = %3f' , t )); frame = getframe ( 1 ); im = frame2im ( frame ); [ imind , cm ] = rgb2ind ( im , 256 ); si t == 0 imwrite ( imind , cm , 'out.gif' , 'gif' , 'Loopcount' , inf , 'DelayTime' , 0.1 ); de lo contrario imwrite ( imind , cm , 'out.gif' , 'gif' , 'WriteMode' , 'append' , 'DelayTime' , 0.1 ); fin fin                                                                  

Operador discreto de Schrödinger

Sea una función potencial definida en el gráfico. Nótese que P puede considerarse un operador multiplicativo que actúa diagonalmente sobre ${\displaystyle P\colon V\rightarrow R}$ ${\displaystyle \phi }$

${\displaystyle (P\phi )(v)=P(v)\phi (v).}$

Entonces está el operador de Schrödinger discreto , un análogo del operador de Schrödinger continuo . ${\displaystyle H=\Delta +P}$

Si el número de aristas que se encuentran en un vértice está uniformemente acotado y el potencial está acotado, entonces H es acotado y autoadjunto .

Las propiedades espectrales de este hamiltoniano se pueden estudiar con el teorema de Stone ; esto es una consecuencia de la dualidad entre posets y álgebras de Boole .

En redes regulares, el operador normalmente tiene soluciones de localización de Anderson y de ondas viajeras , dependiendo de si el potencial es periódico o aleatorio.

La función de Green del operador discreto de Schrödinger se da en el formalismo resolutivo por

${\displaystyle G(v,w;\lambda )=\left\langle \delta _{v}\left|{\frac {1}{H-\lambda }}\right|\delta _{w}\right\rangle }$

donde se entiende que es la función delta de Kronecker en el gráfico: ; es decir, es igual a 1 si v = w y 0 en caso contrario. ${\displaystyle \delta _{w}}$ ${\displaystyle \delta _{w}(v)=\delta _{wv}}$

Para un número fijo y un número complejo, la función de Green considerada como una función de v es la única solución para ${\displaystyle w\in V}$ ${\displaystyle \lambda }$

${\displaystyle (H-\lambda )G(v,w;\lambda )=\delta _{w}(v).}$

Clasificación ADE

Ciertas ecuaciones que involucran al laplaciano discreto solo tienen soluciones en los diagramas de Dynkin de enlaces simples (multiplicidad de todas las aristas 1) y son un ejemplo de la clasificación ADE . En concreto, las únicas soluciones positivas para la ecuación homogénea:

${\displaystyle \Delta \phi =\phi ,}$

en palabras,

"El doble de cualquier etiqueta es la suma de las etiquetas de los vértices adyacentes".

se encuentran en los diagramas de Dynkin ADE extendidos (afines), de los cuales hay 2 familias infinitas (A y D) y 3 excepciones (E). La numeración resultante es única hasta la escala y, si el valor más pequeño se establece en 1, los demás números son enteros, con un rango de hasta 6.

Los gráficos ADE ordinarios son los únicos gráficos que admiten un etiquetado positivo con la siguiente propiedad:

El doble de cualquier etiqueta menos dos es la suma de las etiquetas en los vértices adyacentes.

En términos del Laplaciano, las soluciones positivas de la ecuación no homogénea:

${\displaystyle \Delta \phi =\phi -2.}$

La numeración resultante es única (la escala se especifica con el "2") y consta de números enteros; para E ₈ varían de 58 a 270, y se han observado ya en 1968. ^[15]

Véase también

• Análisis de la forma espectral
• Red eléctrica
• Suma de Kronecker de laplacianos discretos
• Cálculo discreto

Referencias

1. Leventhal, Daniel (otoño de 2011). «Procesamiento de imágenes» (PDF) . Universidad de Washington . Consultado el 1 de diciembre de 2019 .
2. Crane, K.; de Goes, F.; Desbrun, M.; Schröder, P. (2013). "Procesamiento de geometría digital con cálculo exterior discreto". Cursos ACM SIGGRAPH 2013. SIGGRAPH '13. Vol. 7. págs. 1–126. doi :10.1145/2504435.2504442.
3. Reuter, M.; Biasotti, S.; Giorgi, D.; Patane, G.; Spagnuolo, M. (2009). "Operadores discretos de Laplace-Beltrami para análisis de forma y segmentación". Computers & Graphics . 33 (3): 381–390df. CiteSeerX 10.1.1.157.757 . doi :10.1016/j.cag.2009.03.005. 
4. Forsyth, DA; Ponce, J. (2003). "Visión por computadora". Computadoras y gráficos . 33 (3): 381–390. CiteSeerX 10.1.1.157.757 . doi :10.1016/j.cag.2009.03.005. 
5. Matthys, Don (14 de febrero de 2001). "LoG Filter". Universidad Marquette . Consultado el 1 de diciembre de 2019 .
6. Provatas, Nikolas; Anciano, Ken (13 de octubre de 2010). Métodos de campo de fases en ciencia e ingeniería de materiales (PDF) . Weinheim, Alemania: Wiley-VCH Verlag GmbH & Co. KGaA. pag. 219. doi : 10.1002/9783527631520. ISBN 978-3-527-63152-0.
7. O'Reilly, H.; Beck, Jeffrey M. (2006). "Una familia de aproximaciones laplacianas discretas de gran formato en tres dimensiones" (PDF) . Revista internacional de métodos numéricos en ingeniería : 1–16.
8. Lindeberg, T., "Espacio de escala para señales discretas", PAMI(12), No. 3, marzo de 1990, págs. 234–254.
9. Lindeberg, T., Teoría del espacio de escala en visión por computadora, Kluwer Academic Publishers, 1994, ISBN 0-7923-9418-6 . 
10. Patra, Michael; Karttunen, Mikko (2006). "Plantillas con error de discretización isotrópica para operadores diferenciales". Métodos numéricos para ecuaciones diferenciales parciales . 22 (4): 936–953. doi :10.1002/num.20129. ISSN  0749-159X. S2CID  123145969.
11. Bigun, J. (2006). Visión con dirección . Springer. doi :10.1007/b138918. ISBN. 978-3-540-27322-6.
12. Newman, Mark (2010). Redes: una introducción . Oxford University Press. ISBN 978-0199206650.
13. Yavari, R.; Cole, KD; Rao, PK (2020). "Transferencia de calor computacional con teoría de grafos espectrales: verificación cuantitativa". Revista internacional de ciencias térmicas . 153 : 106383. Bibcode :2020IJTS..15306383C. doi : 10.1016/j.ijthermalsci.2020.106383 .
14. Cole, KD; Riensche, A.; Rao, PK (2022). "Funciones de Green discretas y teoría de grafos espectrales para modelado térmico computacionalmente eficiente". Revista internacional de transferencia de calor y masa . 183 : 122112. Código Bibliográfico :2022IJHMT.18322112C. doi : 10.1016/j.ijheatmasstransfer.2021.122112 . S2CID  244652819.
15. Bourbaki, Nicolas (2002) [1968], Groupes et algebres de Lie: Capítulos 4-6, Elementos de matemáticas, traducido por Pressley, Andrew, Springer, ISBN 978-3-540-69171-6

• Sunada, T. (2008). "Análisis geométrico discreto". Análisis de grafos y sus aplicaciones. Actas de simposios sobre matemáticas puras. Vol. 77. American Mathematical Society. págs. 51–86. ISBN 978-0-8218-9384-5.

Enlaces externos

• Ollivier, Yann (2004). "Brecha espectral de un grafo". Archivado desde el original el 23 de mayo de 2007.