Inmersión (matemáticas)

En matemáticas , una inmersión es una función diferenciable entre variedades diferenciables cuyo avance diferencial es en todas partes inyectivo . ^[1] Explícitamente, $f : M \to N$ es una inmersión si

D_{p}f:T_{p}M\to T_{f(p)}N\,

es una función inyectiva en cada punto $p$ de $M$ (donde $T p X$ denota el espacio tangente de una variedad $X$ en un punto $p$ en $X$ ). De manera equivalente, $f$ es una inmersión si su derivada tiene un rango constante igual a la dimensión de $M$ : ^[2]

\operatorname {rango} \,D_{p}f=\dim M.

La función $f$ en sí misma no necesita ser inyectiva, sólo su derivada debe serlo.

Un concepto relacionado es el de incrustación . Una incrustación suave es una inmersión inyectiva f $: M \to N que$ también es una incrustación topológica , de modo que $M$ es difeomorfa a su imagen en $N.$ Una inmersión es precisamente una incrustación local , es decir, para cualquier punto $x \in M$ hay una vecindad , $U \subseteq M$ , de $x$ tal que $f : U \to N$ es una incrustación y, a la inversa, una incrustación local es una inmersión. ^[3] Para variedades de dimensiones infinitas, esto a veces se considera la definición de inmersión. ^[4]

Si $M$ es compacto , una inmersión inyectiva es una incrustación, pero si $M$ no es compacto, entonces las inmersiones inyectables no necesitan ser incrustaciones; comparar con biyecciones continuas versus homeomorfismos .

Homotopía regular

Una homotopía regular entre dos inmersiones $f$ y $g$ de una variedad $M$ a una variedad $N$ se define como una función diferenciable $H : M \times [0,1] \to N$ tal que para todo $t$ en $[0, 1]$ la función $H t : M \to N$ definido por $H t (x) = H (x, t)$ para todo $x \in M$ es una inmersión, con $H 0 = f$ , $H 1 = g$ . Una homotopía regular es, por tanto, una homotopía por inmersión.

Clasificación

Hassler Whitney inició el estudio sistemático de inmersiones y homotopías regulares en la década de 1940, demostrando que para $2 m < n + 1$ cada aplicación $f : M m \to N n$ de una variedad $m$ -dimensional a una variedad $n -dimensional es$ homotópica a una inmersión. , y de hecho a una incrustación durante $2 m < n$ ; estos son el teorema de inmersión de Whitney y el teorema de incrustación de Whitney .

Stephen Smale expresó las clases de homotopía regulares de inmersiones como los grupos de homotopía de una determinada variedad Stiefel . La eversión de la esfera fue una consecuencia particularmente sorprendente. $f:M^{m}\to \mathbb {R} ^{n}$

Morris Hirsch generalizó la expresión de Smale a una descripción de la teoría de la homotopía de las clases regulares de homotopía de inmersiones de cualquier variedad $m -dimensional$ $M m$ en cualquier variedad $n -dimensional$ $N n$ .

La clasificación de inmersiones de Hirsch-Smale fue generalizada por Mikhail Gromov .

Existencia

La tira de Möbius no se sumerge en la codimensión 0 porque su paquete tangente no es trivial.

La principal obstrucción a la existencia de una inmersión es el haz normal estable de $M$ , como lo detectan sus clases características , en particular sus clases de Stiefel-Whitney . Es decir, dado que es paralelizable , el retroceso de su fibrado tangente a $M$ es trivial; dado que este retroceso es la suma directa del paquete tangente (intrínsecamente definido) en $M$ , $TM$ , que tiene dimensión $m$ , y del paquete normal $ν$ de la inmersión $i$ , que tiene dimensión $n$ $-$ $m$ , para que haya una codimensión $k$ inmersión de $M$ , debe haber un paquete vectorial de dimensión $k$ , $ξ$ $k$ , que reemplace al paquete normal $ν$ , tal que sea trivial. Por el contrario, dado tal paquete, una inmersión de $M$ con este paquete normal es equivalente a una inmersión codimensión 0 del espacio total de este paquete, que es una variedad abierta. $i:M^{m}\to \mathbb {R} ^{n}$ $\mathbb {R} ^{n}$ $TM\oplus \zeta ^{k}$

El paquete normal estable es la clase de paquetes normales más paquetes triviales y, por lo tanto, si el paquete normal estable tiene dimensión cohomológica $k$ , no puede provenir de un paquete normal (inestable) de dimensión menor que $k$ . Por lo tanto, la dimensión de cohomología del paquete normal estable, detectada por su clase característica más alta que no desaparece, es una obstrucción para las inmersiones.

Dado que las clases características se multiplican bajo la suma directa de paquetes de vectores, esta obstrucción se puede expresar intrínsecamente en términos del espacio $M$ y su paquete tangente y el álgebra de cohomología. Whitney planteó esta obstrucción (en términos del paquete tangente, no del paquete normal estable).

Por ejemplo, la tira de Möbius tiene un paquete tangente no trivial, por lo que no puede sumergirse en la codimensión 0 (en ), aunque se incrusta en la codimensión 1 (en ). $\mathbb {R} ^{2}$ $\mathbb {R} ^{3}$

William S. Massey (1960) demostró que estas clases características (las clases Stiefel-Whitney del paquete normal estable) desaparecen por encima del grado $n - α (n)$ , donde $α (n)$ es el número de dígitos "1" cuando $n$ es escrito en binario; este límite es agudo, como lo realiza el espacio proyectivo real . Esto dio evidencia de la conjetura de la inmersión , es decir, que cada $n$ -variedad podría sumergirse en la codimensión $n - α (n)$ , es decir, en Esta conjetura fue probada por Ralph Cohen (1985). $\mathbb {R} ^{2n-\alpha (n)}.$

Codimensión 0

Las inmersiones en codimensión 0 son equivalentemente inmersiones en dimensión relativa 0 , y es mejor considerarlas como inmersiones. Una inmersión de codimensión 0 de una variedad cerrada es precisamente un mapa de cobertura , es decir, un haz de fibras con fibra de dimensión 0 (discreta). Según el teorema de Ehresmann y el teorema de Phillips sobre inmersiones, una inmersión adecuada de variedades es un haz de fibras, por lo tanto, las inmersiones/inmersiones de codimensión/dimensión relativa 0/inmersiones se comportan como inmersiones.

Además, las inmersiones de la codimensión 0 no se comportan como otras inmersiones, que están determinadas en gran medida por el paquete normal estable: en la codimensión 0 uno tiene problemas de clase fundamental y espacios de cobertura. Por ejemplo, no existe inmersión en codimensión 0 a pesar de que el círculo es paralelizable, lo que se puede demostrar porque la línea no tiene clase fundamental, por lo que no se obtiene el mapa requerido en la cohomología superior. Alternativamente, esto es por invariancia de dominio . De manera similar, aunque los 3 toros son paralelizables, no hay inmersión : cualquier cubierta de este tipo tendría que ramificarse en algunos puntos, ya que la esfera simplemente está conectada. $\mathbb {S} ^{1}\to \mathbb {R} ^{1},$ $\mathbb {S} ^{3}$ $\mathbb {T} ^{3}$ $\mathbb {T} ^{3}\to \mathbb {S} ^{3}$

Otra forma de entender esto es que una inmersión en codimensión $k$ de una variedad corresponde a una inmersión en codimensión 0 de un haz de vectores $k -dimensional, que es una$ variedad abierta si la codimensión es mayor que 0, pero a una variedad cerrada en codimensión 0 ( si el colector original está cerrado).

Múltiples puntos

Un $k$ -tuple punto (doble, triple, etc.) de una inmersión $f : M \to N$ es un conjunto desordenado ${x 1, ..., x k}$ de puntos distintos $x i \in M$ con la misma imagen $f (x yo) \in norte$ . Si $M$ es una variedad $m -dimensional y$ $N$ es una variedad n -dimensional, entonces para una inmersión $f : M \to N$ en posición general, el conjunto de $k$ -tuple puntos es una variedad $(n - k (n - m))$ -dimensional . Cada incrustación es una inmersión sin múltiples puntos (donde $k > 1$ ). Tenga en cuenta, sin embargo, que lo contrario es falso: hay inmersiones inyectivas que no son incrustaciones.

La naturaleza de los múltiples puntos clasifica las inmersiones; por ejemplo, las inmersiones de un círculo en el plano se clasifican hasta la homotopía regular por el número de puntos dobles.

En un punto clave de la teoría de la cirugía es necesario decidir si la inmersión de una $m$ -esfera en una variedad de $2$ $m$ -dimensional es homotópica regular a una incrustación, en cuyo caso puede eliminarse mediante cirugía. Muro asociado a $f$ un invariante $μ$ $($ $f$ $)$ en un cociente del anillo del grupo fundamental que cuenta los puntos dobles de $f$ en la cobertura universal de $N$ . Para $m$ $> 2$ , $f$ es homotópico regular de una incrustación si y solo si $μ$ $($ $f$ $) = 0$ según el truco de Whitney . $f:\mathbb {S} ^{m}\to N^{2m}$ $\mathbb {Z} [\pi _ {1}(N)]$

Se pueden estudiar las incrustaciones como "inmersiones sin múltiples puntos", ya que las inmersiones son más fáciles de clasificar. Así, se puede partir de inmersiones e intentar eliminar múltiples puntos, viendo si se puede hacerlo sin introducir otras singularidades –estudiando "múltiples disyunciones". Esto fue hecho por primera vez por André Haefliger , y este enfoque es fructífero en la codimensión 3 o más; desde el punto de vista de la teoría de la cirugía, esto es una "(co)dimensión alta", a diferencia de la codimensión 2, que es la dimensión de anudado, como en el nudo. teoría . Se estudia categóricamente mediante el " cálculo de functores " de Thomas Goodwillie, John Klein y Michael S. Weiss.

Ejemplos y propiedades

Una rosa matemática con $k$ pétalos es una inmersión del círculo en el plano con un solo $k$ -tuple punto; $k$ puede ser cualquier número impar, pero si es par debe ser múltiplo de 4, por lo que la figura 8, con $k = 2$ , no es una rosa.
La botella de Klein , y todas las demás superficies cerradas no orientables, pueden sumergirse en 3 espacios pero no incrustarse.
Según el teorema de Whitney-Graustein , las clases de homotopía regulares de inmersiones del círculo en el plano se clasifican por el número de devanado , que es también el número de puntos dobles contados algebraicamente (es decir, con signos).
La esfera se puede dar la vuelta : la incrustación estándar está relacionada con una homotopía regular de inmersiones. $f_{0}:\mathbb {S} ^{2}\to \mathbb {R} ^{3}$ $f_{1}=-f_{0}:\mathbb {S} ^{2}\to \mathbb {R} ^{3}$ $f_{t}:\mathbb {S} ^{2}\to \mathbb {R} ^{3}.$
La superficie de Boy es una inmersión del plano proyectivo real en el espacio tridimensional; por lo tanto también una inmersión 2 a 1 de la esfera.
La superficie de Morin es una inmersión de la esfera; tanto él como la superficie de Boy surgen como modelos intermedios en la eversión de la esfera.

Curvas planas sumergidas

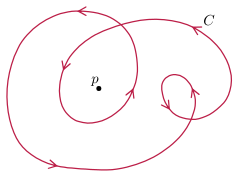
Las curvas planas sumergidas tienen un número de giro bien definido , que se puede definir como la curvatura total dividida por 2 $π$ . Esto es invariante bajo homotopía regular, según el teorema de Whitney-Graustein ; topológicamente, es el grado del mapa de Gauss , o equivalentemente, el número de vueltas de la tangente unitaria (que no desaparece) alrededor del origen. Además, este es un conjunto completo de invariantes : dos curvas planas cualesquiera con el mismo número de giro son homotópicas regulares.

Cada curva plana sumergida se eleva a una curva espacial incrustada separando los puntos de intersección, lo que no ocurre en dimensiones superiores. Con datos agregados (qué hebra está en la parte superior), las curvas planas sumergidas producen diagramas de nudos , que son de interés central en la teoría de nudos . Mientras que las curvas del plano sumergido, hasta la homotopía regular, están determinadas por su número de giros, los nudos tienen una estructura muy rica y compleja.

Superficies inmersas en 3 espacios.

El estudio de superficies sumergidas en 3 espacios está estrechamente relacionado con el estudio de superficies anudadas (incrustadas) en 4 espacios, por analogía con la teoría de los diagramas de nudos (curvas planas inmersas (2 espacios) como proyecciones de curvas anudadas en 3 -espacio): dada una superficie anudada en el 4-espacio, uno puede proyectarla a una superficie sumergida en el 3-espacio, y a la inversa, dada una superficie sumergida en el 3-espacio, uno puede preguntarse si se eleva al 4-espacio - es ¿Es la proyección de una superficie anudada en 4 espacios? Esto permite relacionar preguntas sobre estos objetos.

Un resultado básico, a diferencia del caso de las curvas planas, es que no todas las superficies sumergidas se elevan hasta convertirse en una superficie anudada. ^[5] En algunos casos la obstrucción es de 2-torsión, como en el ejemplo de Koschorke , ^[6] que es una superficie sumergida (formada por 3 bandas de Möbius, con un punto triple ) que no se eleva a una superficie anudada, pero Tiene doble tapa que sí se levanta. Carter y Saito (1998a) ofrecen un análisis detallado, mientras que Carter, Kamada y Saito (2004) ofrecen un estudio más reciente.

Generalizaciones

Una generalización de gran alcance de la teoría de la inmersión es el principio de homotopía : se puede considerar la condición de inmersión (el rango de la derivada es siempre $k$ ) como una relación diferencial parcial (PDR), tal como se puede expresar en términos de las derivadas parciales de la función. Entonces, la teoría de la inmersión de Smale-Hirsch es el resultado de que esto se reduce a la teoría de la homotopía, y el principio de homotopía proporciona condiciones generales y razones para que los PDR se reduzcan a la teoría de la homotopía.

Ver también

Notas

^ Esta definición la dan Bishop & Crittenden 1964, p. 185, cariño 1994, pág. 53, do Carmo 1994, p. 11, Frankel 1997, pág. 169, Gallot, Hulin y Lafontaine 2004, pág. 12, Kobayashi y Nomizu 1963, pág. 9, Kosinski 2007, pág. 27, Székeres 2004, pág. 429.
^ Esta definición la dan Crampin y Pirani 1994, p. 243, Spivak 1999, pág. 46.
^ Este tipo de definición, basada en difeomorfismos locales, la dan Bishop y Goldberg 1968, p. 40, Lang 1999, pág. 26.
^ Este tipo de definición de dimensión infinita la da Lang 1999, p. 26.
^ Carter y Saito 1998; Carter, Kamada y Saito 2004, Observación 1.23, pág. 17
^ Koschorke 1979

Referencias

Adachi, Masahisa (1993), Incrustaciones e inmersiones, traducido por Kiki Hudson, ISBN 978-0-8218-4612-4
Arnoldo, VI ; Varchenko, AN; Gusein-Zade, SM (1985), Singularidades de mapas diferenciables: Volumen 1 , Birkhäuser, ISBN 0-8176-3187-9
Obispo, Richard Lawrence ; Crittenden, Richard J. (1964), Geometría de variedades , Nueva York: Academic Press, ISBN 978-0-8218-2923-3
Obispo, RL ; Goldberg, SI (1968), Análisis tensorial en variedades (primera edición de Dover, 1980), The Macmillan Company, ISBN 0-486-64039-6
Bruce, JW; Giblin, PJ (1984), Curvas y singularidades , Cambridge University Press, ISBN 0-521-42999-4
Carter, J. Scott; Saito, Masahico (1998a), "Superficies en 3 espacios que no se elevan hasta incrustaciones en 4 espacios", Teoría de nudos (Varsovia, 1995) , Banach Center Publ., vol. 42, académico polaco. Sci., Varsovia, págs. 29–47, CiteSeerX 10.1.1.44.1505 , MR 1634445.
Carter, J. Scott; Saito, Masahico (1998), Superficies anudadas y sus diagramas , Estudios y monografías matemáticas, vol. 55, pág. 258, ISBN 978-0-8218-0593-0
Carter, Scott; Kamada, Seiichi; Saito, Masahico (2004), Superficies en 4 espacios , Enciclopedia de Ciencias Matemáticas, vol. 142, Berlín: Springer-Verlag, doi :10.1007/978-3-662-10162-9, ISBN 3-540-21040-7, señor 2060067.
Cohen, Ralph L. (1985), "La conjetura de inmersión para variedades diferenciables", Annals of Mathematics , Second Series, 122 (2): 237–328, doi :10.2307/1971304, JSTOR 1971304, MR 0808220.
Crampín, Michael; Pirani, Felix Arnold Edward (1994), Geometría diferencial aplicable , Cambridge, Inglaterra: Cambridge University Press, ISBN 978-0-521-23190-9
Darling, Richard William Ramsay (1994), Formas y conexiones diferenciales , Cambridge, Reino Unido: Cambridge University Press, Bibcode :1994dfc..book.....D, ISBN 978-0-521-46800-8.
do Carmo, Manfredo Perdigao (1994), Geometría riemanniana , ISBN 978-0-8176-3490-2
Frankel, Theodore (1997), La geometría de la física , Cambridge: Cambridge University Press, ISBN 0-521-38753-1
Gallot, Sylvestre; Hulin, Dominique ; Lafontaine, Jacques (2004), Geometría de Riemann (3.ª ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-20493-0
Gromov, M. (1986), Relaciones diferenciales parciales , Springer, ISBN 3-540-12177-3
Hirsch, Morris W. (1959), "Inmersiones de variedades", Transactions of the American Mathematical Society , 93 (2): 242–276, doi : 10.2307/1993453 , JSTOR 1993453, SEÑOR 0119214.
Kobayashi, Shoshichi; Nomizu, Katsumi (1963), Fundamentos de la geometría diferencial, Volumen 1 , Nueva York: Wiley-Interscience
Koschorke, Ulrich (1979), "Múltiples puntos de inmersiones y el teorema de Kahn-Priddy", Mathematische Zeitschrift , 169 (3): 223–236, doi :10.1007/BF01214837, MR 0554526, S2CID 121273182.
Kosinski, Antoni Albert (2007) [1993], Colectores diferenciales , Mineola, Nueva York: Dover Publications, ISBN 978-0-486-46244-8
Lang, Serge (1999), Fundamentos de geometría diferencial , Textos de posgrado en matemáticas, Nueva York: Springer, ISBN 978-0-387-98593-0
Massey, WS (1960), "Sobre las clases Stiefel-Whitney de una variedad", American Journal of Mathematics , 82 (1): 92–102, doi :10.2307/2372878, JSTOR 2372878, MR 0111053.
Smale, Stephen (1958), "Una clasificación de inmersiones de dos esferas", Transactions of the American Mathematical Society , 90 (2): 281–290, doi : 10.2307/1993205 , JSTOR 1993205, MR 0104227.
Smale, Stephen (1959), "La clasificación de inmersiones de esferas en espacios euclidianos", Annals of Mathematics , Second Series, 69 (2): 327–344, doi :10.2307/1970186, JSTOR 1970186, MR 0105117.
Spivak, Michael (1999) [1970], Una introducción completa a la geometría diferencial (Volumen 1) , Publish or Perish, ISBN 0-914098-70-5
Spring, David (2005), "La edad de oro de la teoría de la inmersión en topología: 1959-1973: un estudio matemático desde una perspectiva histórica", Boletín de la Sociedad Estadounidense de Matemáticas , Nueva serie, 42 (2): 163–180, CiteSeerX 10.1.1.363.913 , doi :10.1090/S0273-0979-05-01048-7, SEÑOR 2133309, S2CID 9237068.
Szekeres, Peter (2004), Un curso de física matemática moderna: grupos, espacio de Hilbert y geometría diferencial , Cambridge, Reino Unido: Cambridge University Press, ISBN 978-0-521-82960-1
Wall, CTC (1999), Cirugía en variedades compactas (PDF) , Encuestas y monografías matemáticas, vol. 69 (Segunda ed.), Providence, RI: Sociedad Matemática Estadounidense, doi :10.1090/surv/069, ISBN 0-8218-0942-3, señor 1687388.

enlaces externos

Inmersión en el Atlas Múltiple
Inmersión de una variedad en la Enciclopedia de Matemáticas.