Tensor de curvatura de Riemann

Campo tensorial en geometría riemanniana

En el campo matemático de la geometría diferencial , el tensor de curvatura de Riemann o tensor de Riemann-Christoffel (en honor a Bernhard Riemann y Elwin Bruno Christoffel ) es la forma más común utilizada para expresar la curvatura de las variedades de Riemann . Asigna un tensor a cada punto de una variedad de Riemann (es decir, es un cuerpo tensorial ). Es un invariante local de las métricas de Riemann que mide la falla de las derivadas covariantes segundas para conmutar. Una variedad de Riemann tiene curvatura cero si y solo si es plana , es decir, localmente isométrica al espacio euclidiano . ^[1] El tensor de curvatura también se puede definir para cualquier variedad pseudo-riemanniana , o de hecho cualquier variedad equipada con una conexión afín .

Es una herramienta matemática central en la teoría de la relatividad general , la teoría moderna de la gravedad . La curvatura del espacio-tiempo es en principio observable a través de la ecuación de desviación geodésica . El tensor de curvatura representa la fuerza de marea experimentada por un cuerpo rígido que se mueve a lo largo de una geodésica en un sentido precisado por la ecuación de Jacobi .

Definición

Sea una variedad riemanniana o pseudo-riemanniana , y sea el espacio de todos los campos vectoriales en . Definimos el tensor de curvatura de Riemann como una función mediante la siguiente fórmula ^[2] donde es la conexión de Levi-Civita : ${\displaystyle (M,g)}$ ${\displaystyle {\mathfrak {X}}(M)}$ ${\displaystyle M}$ ${\displaystyle {\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\rightarrow {\mathfrak {X}}(M)}$ ${\displaystyle \nabla }$

${\displaystyle R(X,Y)Z=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X,Y]}Z}$

o equivalentemente

${\displaystyle R(X,Y)=[\nabla _{X},\nabla _{Y}]-\nabla _{[X,Y]}}$

donde [ X , Y ] es el corchete de Lie de los campos vectoriales y es un conmutador de operadores diferenciales. Resulta que el lado derecho en realidad solo depende del valor de los campos vectoriales en un punto dado, lo cual es notable ya que la derivada covariante de un campo vectorial también depende de los valores de campo en un entorno del punto. Por lo tanto, es un campo tensorial . Para fijo , la transformación lineal también se denomina transformación de curvatura o endomorfismo . Ocasionalmente, el tensor de curvatura se define con el signo opuesto. ${\displaystyle [\nabla _{X},\nabla _{Y}]}$ ${\displaystyle X,Y,Z}$ ${\displaystyle R}$ ${\displaystyle (1,3)}$ ${\displaystyle X,Y}$ ${\displaystyle Z\mapsto R(X,Y)Z}$

El tensor de curvatura mide la no conmutatividad de la derivada covariante y como tal es el obstáculo de integrabilidad para la existencia de una isometría con el espacio euclidiano (llamado, en este contexto, espacio plano ).

Dado que la conexión Levi-Civita no tiene torsión, su curvatura también se puede expresar en términos de la segunda derivada covariante ^[3].

${\textstyle \nabla _{X,Y}^{2}Z=\nabla _{X}\nabla _{Y}Z-\nabla _{\nabla _{X}Y}Z}$

que depende únicamente de los valores de en un punto. La curvatura puede entonces escribirse como ${\displaystyle X,Y}$

${\displaystyle R(X,Y)=\nabla _{X,Y}^{2}-\nabla _{Y,X}^{2}}$

Por lo tanto, el tensor de curvatura mide la no conmutatividad de la segunda derivada covariante. En notación de índice abstracto , el tensor de curvatura de Riemann es también el conmutador de la derivada covariante de un covector arbitrario consigo mismo: ^{[4] [5]} $${\displaystyle R^{d}{}_{cab}Z^{c}=\nabla _{a}\nabla _{b}Z^{d}-\nabla _{b}\nabla _{a}Z^{d}.}$$ ${\displaystyle A_{\nu }}$

${\displaystyle A_{\nu ;\rho \sigma }-A_{\nu ;\sigma \rho }=A_{\beta }R^{\beta }{}_{\nu \rho \sigma }.}$

Esta fórmula se denomina a menudo identidad de Ricci . ^[6] Este es el método clásico utilizado por Ricci y Levi-Civita para obtener una expresión para el tensor de curvatura de Riemann. ^[7] Esta identidad se puede generalizar para obtener los conmutadores para dos derivadas covariantes de tensores arbitrarios de la siguiente manera ^[8]

${\displaystyle {\begin{aligned}&\nabla _{\delta }\nabla _{\gamma }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s}}-\nabla _{\gamma }\nabla _{\delta }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s}}\\[3pt]={}&R^{\alpha _{1}}{}_{\rho \delta \gamma }T^{\rho \alpha _{2}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s}}+\ldots +R^{\alpha _{r}}{}_{\rho \delta \gamma }T^{\alpha _{1}\cdots \alpha _{r-1}\rho }{}_{\beta _{1}\cdots \beta _{s}}-R^{\sigma }{}_{\beta _{1}\delta \gamma }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\sigma \beta _{2}\cdots \beta _{s}}-\ldots -R^{\sigma }{}_{\beta _{s}\delta \gamma }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s-1}\sigma }\end{aligned}}}$

Esta fórmula también se aplica a las densidades tensoriales sin alteración, porque para la conexión Levi-Civita ( no genérica ) se obtiene: ^[6]

${\displaystyle \nabla _{\mu }\left({\sqrt {g}}\right)\equiv \left({\sqrt {g}}\right)_{;\mu }=0,}$

dónde

${\displaystyle g=\left|\det \left(g_{\mu \nu }\right)\right|.}$

A veces es conveniente definir también la versión puramente covariante del tensor de curvatura mediante

${\displaystyle R_{\sigma \mu \nu \rho }=g_{\rho \zeta }R^{\zeta }{}_{\sigma \mu \nu }.}$

Significado geométrico

Figura que muestra el significado geométrico del tensor de curvatura de Riemann en una variedad esférica curvada. El hecho de que esta transferencia pueda definir dos flechas diferentes en el punto de partida da lugar al tensor de curvatura de Riemann. El símbolo ortogonal indica que el producto escalar (proporcionado por el tensor métrico) entre las flechas transmitidas (o las flechas tangentes en la curva) es cero. El ángulo entre las dos flechas es cero cuando el espacio es plano y mayor que cero cuando el espacio es curvo. Cuanto más curvo sea el espacio, mayor será el ángulo.

De manera informal

Se pueden ver los efectos del espacio curvo comparando una cancha de tenis con la Tierra. Comienza en la esquina inferior derecha de la cancha de tenis, con una raqueta apuntando hacia el norte. Luego, mientras caminas alrededor del contorno de la cancha, en cada paso asegúrate de que la raqueta de tenis se mantenga en la misma orientación, paralela a sus posiciones anteriores. Una vez que se complete el bucle, la raqueta de tenis estará paralela a su posición inicial. Esto se debe a que las canchas de tenis están construidas de manera que la superficie sea plana. Por otro lado, la superficie de la Tierra es curva: podemos completar un bucle en la superficie de la Tierra. Comenzando en el ecuador, apunta una raqueta de tenis hacia el norte a lo largo de la superficie de la Tierra. Una vez más, la raqueta de tenis siempre debe permanecer paralela a su posición anterior, utilizando el plano local del horizonte como referencia. Para este camino, primero camina hacia el polo norte, luego camina de lado (es decir, sin girar), luego hacia abajo hasta el ecuador y finalmente camina hacia atrás hasta tu posición inicial. Ahora la raqueta de tenis estará apuntando hacia el oeste, aunque cuando comenzaste tu viaje apuntaba hacia el norte y nunca giraste tu cuerpo. Este proceso es similar al transporte paralelo de un vector a lo largo de la trayectoria y la diferencia identifica cómo las líneas que parecen "rectas" solo lo son localmente. Cada vez que se completa un bucle, la raqueta de tenis se desviará más de su posición inicial en una cantidad que depende de la distancia y la curvatura de la superficie. Es posible identificar trayectorias a lo largo de una superficie curva donde el transporte paralelo funciona como lo hace en el espacio plano. Estas son las geodésicas del espacio, por ejemplo, cualquier segmento de un gran círculo de una esfera.

El concepto de espacio curvo en matemáticas difiere del uso coloquial. Por ejemplo, si el proceso anterior se completara en un cilindro, se descubriría que no es curvo en general, ya que la curvatura alrededor del cilindro se cancela con la planitud a lo largo del cilindro, lo que es una consecuencia de la curvatura gaussiana y del teorema egregio de Gauss . Un ejemplo conocido de esto es una porción de pizza blanda, que permanecerá rígida a lo largo de su longitud si se curva a lo ancho.

El tensor de curvatura de Riemann es una forma de capturar una medida de la curvatura intrínseca. Cuando se escribe en términos de sus componentes (como cuando se escriben los componentes de un vector), consiste en una matriz multidimensional de sumas y productos de derivadas parciales (algunas de esas derivadas parciales pueden considerarse como algo similar a capturar la curvatura impuesta a alguien que camina en línea recta sobre una superficie curva).

Formalmente

Cuando un vector en un espacio euclidiano se transporta en paralelo alrededor de un bucle, volverá a apuntar en la dirección inicial después de regresar a su posición original. Sin embargo, esta propiedad no se cumple en el caso general. El tensor de curvatura de Riemann mide directamente el fallo de esto en una variedad riemanniana general . Este fallo se conoce como la no holonomía de la variedad.

Sea una curva en una variedad de Riemann . Denote por el mapa de transporte paralelo a lo largo de . Los mapas de transporte paralelo están relacionados con la derivada covariante por ${\displaystyle x_{t}}$ ${\displaystyle M}$ ${\displaystyle \tau _{x_{t}}:T_{x_{0}}M\to T_{x_{t}}M}$ ${\displaystyle x_{t}}$

${\displaystyle \nabla _{{\dot {x}}_{0}}Y=\lim _{h\to 0}{\frac {1}{h}}\left(Y_{x_{0}}-\tau _{x_{h}}^{-1}\left(Y_{x_{h}}\right)\right)=\left.{\frac {d}{dt}}\left(\tau _{x_{t}}^{-1}(Y_{x_{t}})\right)\right|_{t=0}}$

para cada campo vectorial definido a lo largo de la curva. ${\displaystyle Y}$

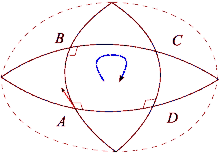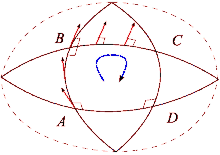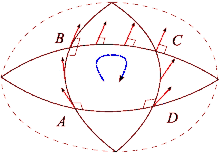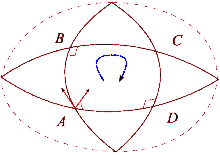
Supóngase que y son un par de campos vectoriales conmutativos. Cada uno de estos campos genera un grupo de difeomorfismos de un parámetro en un entorno de . Denotemos por y , respectivamente, los transportes paralelos a lo largo de los flujos de y para el tiempo . El transporte paralelo de un vector alrededor del cuadrilátero de lados , , , está dado por ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle x_{0}}$ ${\displaystyle \tau _{tX}}$ ${\displaystyle \tau _{tY}}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle t}$ ${\displaystyle Z\in T_{x_{0}}M}$ ${\displaystyle tY}$ ${\displaystyle sX}$ ${\displaystyle -tY}$ ${\displaystyle -sX}$

${\displaystyle \tau _{sX}^{-1}\tau _{tY}^{-1}\tau _{sX}\tau _{tY}Z.}$

La diferencia entre esto y mide la falla del transporte paralelo para regresar a su posición original en el espacio tangente . Al reducir el bucle mediante el envío, se obtiene la descripción infinitesimal de esta desviación: ${\displaystyle Z}$ ${\displaystyle Z}$ ${\displaystyle T_{x_{0}}M}$ ${\displaystyle s,t\to 0}$

${\displaystyle \left.{\frac {d}{ds}}{\frac {d}{dt}}\tau _{sX}^{-1}\tau _{tY}^{-1}\tau _{sX}\tau _{tY}Z\right|_{s=t=0}=\left(\nabla _{X}\nabla _{Y}-\nabla _{Y}\nabla _{X}-\nabla _{[X,Y]}\right)Z=R(X,Y)Z}$

¿Dónde está el tensor de curvatura de Riemann? ${\displaystyle R}$

Expresión de coordenadas

Al convertir a la notación de índice tensorial , el tensor de curvatura de Riemann se expresa mediante

${\displaystyle R^{\rho }{}_{\sigma \mu \nu }=dx^{\rho }\left(R\left(\partial _{\mu },\partial _{\nu }\right)\partial _{\sigma }\right)}$

¿Dónde están los campos de vectores de coordenadas? La expresión anterior se puede escribir utilizando símbolos de Christoffel : ${\displaystyle \partial _{\mu }=\partial /\partial x^{\mu }}$

${\displaystyle R^{\rho }{}_{\sigma \mu \nu }=\partial _{\mu }\Gamma ^{\rho }{}_{\nu \sigma }-\partial _{\nu }\Gamma ^{\rho }{}_{\mu \sigma }+\Gamma ^{\rho }{}_{\mu \lambda }\Gamma ^{\lambda }{}_{\nu \sigma }-\Gamma ^{\rho }{}_{\nu \lambda }\Gamma ^{\lambda }{}_{\mu \sigma }}$

(Véase también Lista de fórmulas en geometría de Riemann ).

Simetrías e identidades

El tensor de curvatura de Riemann tiene las siguientes simetrías e identidades:

donde el corchete se refiere al producto interno en el espacio tangente inducido por el tensor métrico y los corchetes y paréntesis en los índices denotan los operadores de antisimetrización y simetrización , respectivamente. Si hay torsión distinta de cero , las identidades de Bianchi involucran al tensor de torsión . ${\displaystyle \langle ,\rangle }$

La primera identidad de Bianchi (algebraica) fue descubierta por Ricci , pero a menudo se la llama primera identidad de Bianchi o identidad de Bianchi algebraica , porque parece similar a la identidad de Bianchi diferencial. ^{[ cita requerida ]}

Las tres primeras identidades forman una lista completa de simetrías del tensor de curvatura, es decir, dado cualquier tensor que satisfaga las identidades anteriores, se puede encontrar una variedad de Riemann con dicho tensor de curvatura en algún punto. Cálculos simples muestran que dicho tensor tiene componentes independientes. ^[9] La simetría de intercambio se deduce de esto. Las simetrías algebraicas también son equivalentes a decir que R pertenece a la imagen del simetrizador de Young correspondiente a la partición 2+2. ${\displaystyle n^{2}\left(n^{2}-1\right)/12}$

En una variedad de Riemann se tiene la derivada covariante y la identidad de Bianchi (a menudo llamada segunda identidad de Bianchi o identidad de Bianchi diferencial) toma la forma de la última identidad de la tabla. ${\displaystyle \nabla _{u}R}$

Curvatura de Ricci

El tensor de curvatura de Ricci es la contracción del primer y tercer índice del tensor de Riemann.

${\displaystyle \underbrace {R_{ab}} _{\text{Ricci}}\equiv R^{c}{}_{acb}=g^{cd}\underbrace {R_{cadb}} _{\text{Riemann}}}$

Casos especiales

Superficies

Para una superficie bidimensional , las identidades de Bianchi implican que el tensor de Riemann tiene solo un componente independiente, lo que significa que el escalar de Ricci determina completamente el tensor de Riemann. Solo hay una expresión válida para el tensor de Riemann que se ajusta a las simetrías requeridas:

${\displaystyle R_{abcd}=f(R)\left(g_{ac}g_{db}-g_{ad}g_{cb}\right)}$

y contrayendo con la métrica dos veces encontramos la forma explícita:

${\displaystyle R_{abcd}=K\left(g_{ac}g_{db}-g_{ad}g_{cb}\right),}$

donde es el tensor métrico y es una función llamada curvatura gaussiana y , , y toman valores 1 o 2. El tensor de Riemann tiene solo un componente funcionalmente independiente. La curvatura gaussiana coincide con la curvatura seccional de la superficie. También es exactamente la mitad de la curvatura escalar de la 2-variedad, mientras que el tensor de curvatura de Ricci de la superficie está dado simplemente por ${\displaystyle g_{ab}}$ ${\displaystyle K=R/2}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$

${\displaystyle R_{ab}=Kg_{ab}.}$

Formas espaciales

Una variedad de Riemann es una forma espacial si su curvatura seccional es igual a una constante . El tensor de Riemann de una forma espacial está dado por ${\displaystyle K}$

${\displaystyle R_{abcd}=K\left(g_{ac}g_{db}-g_{ad}g_{cb}\right).}$

Por el contrario, excepto en la dimensión 2, si la curvatura de una variedad de Riemann tiene esta forma para alguna función , entonces las identidades de Bianchi implican que es constante y, por lo tanto, que la variedad es (localmente) una forma espacial. ${\displaystyle K}$ ${\displaystyle K}$

Véase también

• Introducción a las matemáticas de la relatividad general
• Descomposición del tensor de curvatura de Riemann
• Curvatura de las variedades de Riemann
• Tensor de curvatura de Ricci

Citas

1. Lee 2018, pág. 193.
2. Lee 2018, pág. 196.
3. Lawson, H. Blaine Jr.; Michelsohn, Marie-Louise (1989). Geometría del espín . Princeton U Press. pág. 154. ISBN 978-0-691-08542-5.
4. Synge JL, Schild A. (1949). Cálculo tensorial. Primera edición de Dover Publications de 1978. Págs. 83, 107. ISBN 978-0-486-63612-2.
5. PAM Dirac (1996). Teoría general de la relatividad . Princeton University Press . ISBN 978-0-691-01146-2.
6. Lovelock, David; Rund, Hanno (1989) [1975]. Tensores, formas diferenciales y principios variacionales . Dover. pág. 84,109. ISBN 978-0-486-65840-7.
7. Ricci, Gregorio ; Levi-Civita, Tullio (marzo de 1900), "Méthodes de calcul différentiel absolu et leurs apps", Mathematische Annalen , 54 (1–2): 125–201, doi :10.1007/BF01454201, S2CID  120009332
8. Sandberg, Vernon D (1978). "Armónicos esféricos tensoriales en S 2 y S 3 como problemas de valores propios" (PDF) . Journal of Mathematical Physics . 19 (12): 2441–2446. Bibcode :1978JMP....19.2441S. doi :10.1063/1.523649.
9. Bergmann PG (1976). Introducción a la teoría de la relatividad. Dover. pp. 172-174. ISBN 978-0-486-63282-7.

Referencias

• Lee, John M. (2018). Introducción a las variedades de Riemann . Springer-Verlag . ISBN 978-3-319-91754-2.
• Besse, AL (1987), Colectores de Einstein , Springer, ISBN 0-387-15279-2
• Kobayashi, S.; Nomizu, K. (1963), Fundamentos de geometría diferencial , vol. 1, Interscience
• Misner, Charles W. ; Thorne, Kip S. ; Wheeler, John A. (1973), Gravitación , WH Freeman, ISBN 978-0-7167-0344-0