La entropía es una de las pocas magnitudes de las ciencias físicas que requieren una dirección particular para el tiempo , a veces llamada flecha del tiempo . A medida que uno avanza "hacia adelante" en el tiempo, dice la segunda ley de la termodinámica , la entropía de un sistema aislado puede aumentar, pero no disminuir . Por lo tanto, la medición de la entropía es una forma de distinguir el pasado del futuro . En los sistemas termodinámicos que no están aislados, la entropía local puede disminuir con el tiempo, acompañada de un aumento de entropía compensatorio en los alrededores ; los ejemplos incluyen objetos que experimentan enfriamiento , sistemas vivos y la formación de cristales típicos .
Al igual que la temperatura , a pesar de ser un concepto abstracto, todos tenemos un sentido intuitivo de los efectos de la entropía. Por ejemplo, a menudo es muy fácil notar la diferencia entre un video que se reproduce hacia adelante o hacia atrás. Un video puede mostrar un fuego de leña que derrite un bloque de hielo cercano; reproducido al revés, mostraría un charco de agua que convierte una nube de humo en madera sin quemar y se congela en el proceso. Sorprendentemente, en ambos casos, la gran mayoría de las leyes de la física no se rompen por estos procesos, siendo la segunda ley de la termodinámica una de las únicas excepciones. Cuando una ley de la física se aplica igualmente cuando el tiempo se invierte, se dice que muestra simetría T ; en este caso, la entropía es lo que permite decidir si el video descrito anteriormente se reproduce hacia adelante o hacia atrás, ya que intuitivamente identificamos que solo cuando se reproduce hacia adelante la entropía de la escena aumenta. Debido a la segunda ley de la termodinámica, la entropía evita que los procesos macroscópicos muestren simetría T.
Cuando se estudia a escala microscópica, no se pueden hacer los juicios anteriores. Al observar una sola partícula de humo sacudida por el aire , no quedaría claro si un video se está reproduciendo hacia adelante o hacia atrás y, de hecho, no sería posible, ya que las leyes que se aplican muestran simetría T. A medida que se desplaza hacia la izquierda o hacia la derecha, cualitativamente no parece diferente; solo cuando se estudia el gas a escala macroscópica se hacen visibles los efectos de la entropía (véase la paradoja de Loschmidt ). En promedio, se esperaría que las partículas de humo alrededor de una cerilla encendida se alejaran unas de otras, difundiéndose por todo el espacio disponible. Sería un evento astronómicamente improbable que todas las partículas se agrupen, pero no se puede predecir el movimiento de ninguna partícula de humo.
Por el contrario, ciertas interacciones subatómicas que involucran la fuerza nuclear débil violan la conservación de la paridad , pero sólo en muy raras ocasiones. [1] Según el teorema CPT , esto significa que también deberían ser irreversibles en el tiempo , y por lo tanto establecer una flecha del tiempo. Sin embargo, esto no está vinculado con la flecha termodinámica del tiempo, ni tiene nada que ver con la experiencia diaria de la irreversibilidad del tiempo. [2]
La segunda ley de la termodinámica permite que la entropía permanezca igual independientemente de la dirección del tiempo. Si la entropía es constante en cualquier dirección del tiempo, no habría una dirección preferida. Sin embargo, la entropía solo puede ser constante si el sistema está en el estado de desorden más alto posible, como un gas que siempre estuvo, y siempre estará, uniformemente distribuido en su recipiente. La existencia de una flecha termodinámica del tiempo implica que el sistema está altamente ordenado solo en una dirección del tiempo, que por definición sería el "pasado". Por lo tanto, esta ley se refiere a las condiciones de contorno en lugar de a las ecuaciones de movimiento .
La segunda ley de la termodinámica es de naturaleza estadística y, por lo tanto, su fiabilidad surge de la enorme cantidad de partículas presentes en los sistemas macroscópicos. En principio, no es imposible que todos los 6 × 10 23 átomos de un mol de gas migren espontáneamente a la mitad de un recipiente; es sólo increíblemente improbable, tan improbable que nunca se ha observado una violación macroscópica de la segunda ley.
La flecha termodinámica se relaciona a menudo con la flecha cosmológica del tiempo, porque en última instancia se trata de las condiciones límite del universo primitivo. Según la teoría del Big Bang , el Universo inicialmente era muy caliente y su energía se distribuía de manera uniforme. Para un sistema en el que la gravedad es importante, como el universo, este es un estado de baja entropía (en comparación con un estado de alta entropía en el que toda la materia colapsó en agujeros negros , un estado al que el sistema puede llegar a evolucionar). A medida que el Universo crece, su temperatura desciende, lo que deja menos energía [por unidad de volumen de espacio] disponible para realizar trabajo en el futuro que la que había disponible en el pasado. Además, las perturbaciones en la densidad de energía aumentan (lo que finalmente forma galaxias y estrellas ). Por lo tanto, el Universo en sí tiene una flecha termodinámica del tiempo bien definida. Pero esto no aborda la cuestión de por qué el estado inicial del universo era el de baja entropía. Si la expansión cósmica se detuviera y se revirtiera debido a la gravedad, la temperatura del Universo volvería a aumentar, pero su entropía también seguiría aumentando debido al continuo crecimiento de las perturbaciones y la eventual formación de un agujero negro, [3] hasta las últimas etapas del Big Crunch , cuando la entropía sería menor que ahora. [ cita requerida ]
Consideremos la situación en la que un recipiente grande está lleno de dos líquidos separados, por ejemplo, un tinte en un lado y agua en el otro. Sin una barrera entre los dos líquidos, el movimiento aleatorio de sus moléculas hará que se mezclen más a medida que pasa el tiempo. Sin embargo, si el tinte y el agua se mezclan, no se espera que se separen de nuevo cuando se dejan solos. Una película de la mezcla parecería realista si se reprodujera hacia adelante, pero irreal si se reprodujera hacia atrás.
Si se observa el recipiente grande al principio del proceso de mezcla, es posible que se encuentre mezclado solo parcialmente. Sería razonable concluir que, sin intervención externa, el líquido alcanzó este estado porque estaba más ordenado en el pasado, cuando había mayor separación, y estará más desordenado o mezclado en el futuro.
Ahora imaginemos que se repite el experimento, esta vez con sólo unas pocas moléculas, quizá diez, en un recipiente muy pequeño. Es fácil imaginar que, observando el movimiento aleatorio de las moléculas, podría ocurrir —por pura casualidad— que las moléculas se segregaran perfectamente, con todas las moléculas de colorante en un lado y todas las moléculas de agua en el otro. El teorema de fluctuación puede concluir que es de esperar que esto ocurra de vez en cuando ; por lo tanto, no es imposible que las moléculas se segreguen por sí mismas. Sin embargo, para un gran número de moléculas es tan improbable que habría que esperar, en promedio, mucho más tiempo que la edad actual del universo para que esto ocurriera. Por lo tanto, una película que mostrara un gran número de moléculas segregándose por sí mismas como se describió anteriormente parecería poco realista y uno se sentiría inclinado a decir que la película se está reproduciendo al revés. Véase la segunda ley de Boltzmann como ley del desorden .
Las matemáticas detrás de la flecha del tiempo , la entropía y la base de la segunda ley de la termodinámica se derivan de la siguiente configuración, tal como lo detallaron Carnot (1824), Clapeyron (1832) y Clausius (1854):
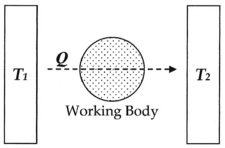
Aquí, como demuestra la experiencia común, cuando un cuerpo caliente T 1 , como un horno, se pone en contacto físico, como al conectarlo a través de un cuerpo de fluido ( cuerpo de trabajo ), con un cuerpo frío T 2 , como una corriente de agua fría, la energía fluirá invariablemente de caliente a frío en forma de calor Q , y dado el tiempo el sistema alcanzará el equilibrio . La entropía, definida como Q/T, fue concebida por Rudolf Clausius como una función para medir la irreversibilidad molecular de este proceso, es decir, el trabajo disipativo que los átomos y las moléculas realizan entre sí durante la transformación.
En este diagrama, se puede calcular el cambio de entropía Δ S para el paso de la cantidad de calor Q desde la temperatura T 1 , a través del "cuerpo de trabajo" del fluido (ver máquina térmica ), que era típicamente un cuerpo de vapor, hasta la temperatura T 2 . Además, se podría suponer, a modo de argumento, que el cuerpo de trabajo contiene sólo dos moléculas de agua.
A continuación, si hacemos la asignación, como la hizo originalmente Clausius:
Entonces el cambio de entropía o "valor de equivalencia" para esta transformación es:
Lo cual es igual a:
y al factorizar Q, tenemos la siguiente forma, tal como la derivó Clausius:
Así, por ejemplo, si Q fuese 50 unidades, T 1 fuese inicialmente 100 grados y T 2 fuese 1 grado, entonces el cambio de entropía para este proceso sería 49,5. Por lo tanto, la entropía aumentó para este proceso, el proceso tomó una cierta cantidad de "tiempo", y uno puede correlacionar el aumento de entropía con el paso del tiempo. Para esta configuración del sistema, posteriormente, es una "regla absoluta". Esta regla se basa en el hecho de que todos los procesos naturales son irreversibles en virtud del hecho de que las moléculas de un sistema, por ejemplo dos moléculas en un tanque, no solo realizan trabajo externo (como empujar un pistón), sino que también realizan trabajo interno entre sí, en proporción al calor utilizado para realizar el trabajo (ver: Equivalente mecánico del calor ) durante el proceso. La entropía explica el hecho de que existe fricción intermolecular interna.
Una diferencia importante entre el pasado y el futuro es que en cualquier sistema (como un gas de partículas) sus condiciones iniciales son usualmente tales que sus diferentes partes no están correlacionadas, pero a medida que el sistema evoluciona y sus diferentes partes interactúan entre sí, se correlacionan. [4] Por ejemplo, siempre que se trata de un gas de partículas, siempre se supone que sus condiciones iniciales son tales que no hay correlación entre los estados de las diferentes partículas (es decir, las velocidades y ubicaciones de las diferentes partículas son completamente aleatorias, hasta la necesidad de ajustarse al macroestado del sistema). Esto está estrechamente relacionado con la segunda ley de la termodinámica: por ejemplo, en un sistema finito que interactúa con reservorios de calor finitos, la entropía es equivalente a las correlaciones sistema-reservorio, y por lo tanto ambas aumentan juntas. [5]
Tomemos como ejemplo (experimento A) una caja cerrada que, al principio, está medio llena de gas ideal. A medida que pasa el tiempo, el gas obviamente se expande para llenar toda la caja, de modo que el estado final es una caja llena de gas. Este es un proceso irreversible, ya que si la caja está llena al principio (experimento B), no se llena solo hasta la mitad después, excepto en la situación muy improbable en que las partículas de gas tengan posiciones y velocidades muy especiales. Pero esto se debe precisamente a que siempre asumimos que las condiciones iniciales en el experimento B son tales que las partículas tienen posiciones y velocidades aleatorias. Esto no es correcto para las condiciones finales del sistema en el experimento A, porque las partículas han interactuado entre sí, de modo que sus posiciones y velocidades se han vuelto dependientes entre sí, es decir, correlacionadas. Esto se puede entender si miramos el experimento A hacia atrás en el tiempo, que llamaremos experimento C: ahora comenzamos con una caja llena de gas, pero las partículas no tienen posiciones y velocidades aleatorias; Más bien, sus posiciones y velocidades son tan particulares que, después de un tiempo, todas se mueven a una mitad de la caja, que es el estado final del sistema (¡este es el estado inicial del experimento A, porque ahora estamos viendo el mismo experimento al revés!). Las interacciones entre partículas ahora no crean correlaciones entre las partículas, sino que de hecho las convierten en (al menos aparentemente) aleatorias, "cancelando" las correlaciones preexistentes. [ cita requerida ] La única diferencia entre el experimento C (que desafía la Segunda Ley de la Termodinámica) y el experimento B (que obedece a la Segunda Ley de la Termodinámica) es que en el primero las partículas no están correlacionadas al final, mientras que en el segundo las partículas no están correlacionadas al principio. [ cita requerida ]
De hecho, si todos los procesos físicos microscópicos son reversibles (véase la discusión a continuación), entonces la Segunda Ley de la Termodinámica puede ser probada para cualquier sistema aislado de partículas con condiciones iniciales en las que los estados de las partículas no están correlacionados. Para hacer esto, uno debe reconocer la diferencia entre la entropía medida de un sistema, que depende solo de su macroestado (su volumen, temperatura, etc.) y su entropía de información , [6] que es la cantidad de información (número de bits de computadora) necesaria para describir el microestado exacto del sistema. La entropía medida es independiente de las correlaciones entre partículas en el sistema, porque no afectan a su macroestado, pero la entropía de información sí depende de ellas, porque las correlaciones reducen la aleatoriedad del sistema y, por lo tanto, reducen la cantidad de información necesaria para describirlo. [7] Por lo tanto, en ausencia de tales correlaciones, las dos entropías son idénticas, pero por lo demás la entropía de información es menor que la entropía medida, y la diferencia puede usarse como una medida de la cantidad de correlaciones.
Ahora bien, según el teorema de Liouville , la inversión temporal de todos los procesos microscópicos implica que la cantidad de información necesaria para describir el microestado exacto de un sistema aislado (su entropía conjunta teórica de la información ) es constante en el tiempo. Esta entropía conjunta es igual a la entropía marginal (entropía suponiendo que no hay correlaciones) más la entropía de correlación (entropía mutua, o su información mutua negativa ). Si suponemos que no hay correlaciones entre las partículas inicialmente, entonces esta entropía conjunta es simplemente la entropía marginal, que es simplemente la entropía termodinámica inicial del sistema, dividida por la constante de Boltzmann . [ cita requerida ] Sin embargo, si estas son de hecho las condiciones iniciales (y este es un supuesto crucial), entonces tales correlaciones se forman con el tiempo. En otras palabras, hay una entropía mutua decreciente (o información mutua creciente), y durante un tiempo que no es demasiado largo, las correlaciones (información mutua) entre partículas solo aumentan con el tiempo. Por lo tanto, la entropía termodinámica, que es proporcional a la entropía marginal, también debe aumentar con el tiempo [8] (nótese que "no demasiado largo" en este contexto es relativo al tiempo necesario, en una versión clásica del sistema, para que pase por todos sus posibles microestados, un tiempo que puede estimarse aproximadamente como , donde es el tiempo entre colisiones de partículas y S es la entropía del sistema. En cualquier caso práctico, este tiempo es enorme comparado con todo lo demás). Nótese que la correlación entre partículas no es una cantidad completamente objetiva. No se puede medir la entropía mutua, solo se puede medir su cambio, asumiendo que se puede medir un microestado. [ cita requerida ] La termodinámica está restringida al caso en el que no se pueden distinguir los microestados, lo que significa que solo se puede medir la entropía marginal, proporcional a la entropía termodinámica, y, en un sentido práctico, siempre aumenta.
Los fenómenos que ocurren de manera diferente según su dirección temporal pueden vincularse en última instancia a la segunda ley de la termodinámica [ cita requerida ] , por ejemplo, los cubitos de hielo se derriten en el café caliente en lugar de ensamblarse a partir del café y un bloque que se desliza sobre una superficie rugosa disminuye su velocidad en lugar de aumentarla. La idea de que podemos recordar el pasado y no el futuro se llama la "flecha psicológica del tiempo" y tiene profundas conexiones con el demonio de Maxwell y la física de la información; la memoria está vinculada a la segunda ley de la termodinámica si uno la ve como correlación entre las células cerebrales (o bits de computadora) y el mundo exterior: dado que tales correlaciones aumentan con el tiempo, la memoria está vinculada a eventos pasados, en lugar de a eventos futuros [ cita requerida ] .
La investigación actual se centra principalmente en describir matemáticamente la flecha termodinámica del tiempo, ya sea en sistemas clásicos o cuánticos, y en comprender su origen desde el punto de vista de las condiciones de contorno cosmológicas .
Algunas investigaciones actuales en sistemas dinámicos indican una posible "explicación" para la flecha del tiempo. [ cita requerida ] Hay varias formas de describir la evolución temporal de un sistema dinámico. En el marco clásico, se considera una ecuación diferencial ordinaria , donde el parámetro es explícitamente el tiempo. Por la naturaleza misma de las ecuaciones diferenciales, las soluciones de tales sistemas son inherentemente reversibles en el tiempo. Sin embargo, muchos de los casos interesantes son ergódicos o mixtos , y se sospecha firmemente que la mezcla y la ergodicidad de alguna manera subyacen al mecanismo fundamental de la flecha del tiempo. Si bien la fuerte sospecha puede ser solo una sensación fugaz de intuición, no se puede negar que, cuando hay múltiples parámetros, entra en juego el campo de las ecuaciones diferenciales parciales . En tales sistemas, está en juego la fórmula de Feynman-Kac , que asegura para casos específicos, una correspondencia uno a uno entre la ecuación diferencial estocástica lineal específica y la ecuación diferencial parcial. Por lo tanto, cualquier sistema de ecuaciones diferenciales parciales equivale a un sistema aleatorio de un solo parámetro, que no es reversible debido a la correspondencia antes mencionada. [9]
Los sistemas ergódicos y de mezcla no tienen soluciones exactas, y por lo tanto probar la irreversibilidad del tiempo en un sentido matemático es (a partir de 2006 [update]) imposible. [ cita requerida ] El concepto de soluciones "exactas" es antrópico . ¿"Exacto" significa lo mismo que forma cerrada en términos de expresiones ya conocidas, o significa simplemente una única secuencia finita de trazos de un/el utensilio de escritura/dedo humano? Hay una miríada de sistemas conocidos por la humanidad que son abstractos y tienen definiciones recursivas, pero actualmente no existe una notación no autorreferencial. Como resultado de esta complejidad, es natural buscar en otros lugares ejemplos y perspectivas diferentes. Se pueden lograr algunos avances estudiando modelos de tiempo discreto o ecuaciones diferenciales . Muchos modelos de tiempo discreto, como las funciones iteradas que se consideran en los programas populares de dibujo fractal, no son explícitamente reversibles en el tiempo, ya que cualquier punto dado "en el presente" puede tener varios "pasados" diferentes asociados a él: de hecho, el conjunto de todos los pasados se conoce como el conjunto de Julia . Dado que estos sistemas tienen una irreversibilidad incorporada, no es apropiado usarlos para explicar por qué el tiempo no es reversible.
Existen otros sistemas que son caóticos y que también son explícitamente reversibles en el tiempo: entre ellos se encuentra el mapa de Baker , que también es exactamente solucionable. Una interesante vía de estudio es examinar las soluciones de tales sistemas no iterando el sistema dinámico a lo largo del tiempo, sino estudiando el operador de Frobenius-Perron o el operador de transferencia correspondiente para el sistema. Para algunos de estos sistemas, se puede demostrar matemáticamente de forma explícita que los operadores de transferencia no son de clase traza . Esto significa que estos operadores no tienen un espectro de valores propios único que sea independiente de la elección de la base. En el caso del mapa de Baker, se puede demostrar que existen varias diagonalizaciones o bases únicas e inequivalentes, cada una con un conjunto diferente de valores propios. Es este fenómeno el que se puede ofrecer como una "explicación" para la flecha del tiempo. Es decir, aunque el sistema iterado de tiempo discreto es explícitamente simétrico en el tiempo, el operador de transferencia no lo es. Además, el operador de transferencia puede diagonalizarse de una de dos maneras desiguales: una que describe la evolución del sistema en el tiempo hacia adelante y otra que describe la evolución en el tiempo hacia atrás.
Hasta 2006, este tipo de ruptura de simetría temporal se ha demostrado solo para un número muy pequeño de sistemas de tiempo discreto y exactamente solucionables. El operador de transferencia para sistemas más complejos no se ha formulado de manera consistente, y su definición precisa está plagada de una variedad de dificultades sutiles. En particular, no se ha demostrado que tenga una simetría rota para los sistemas ergódicos de tiempo continuo y exactamente solucionables más simples, como el billar de Hadamard o el flujo de Anosov en el espacio tangente de PSL(2,R) .
La investigación sobre la irreversibilidad en la mecánica cuántica toma varias direcciones diferentes. Una de ellas es el estudio de los espacios de Hilbert manipulados y, en particular, de cómo se entremezclan los espectros de valores propios discretos y continuos [ cita requerida ] . Por ejemplo, los números racionales están completamente entremezclados con los números reales y, sin embargo, tienen un conjunto único y distinto de propiedades. Se espera que el estudio de los espacios de Hilbert con una entremezcla similar proporcione información sobre la flecha del tiempo.
Otro enfoque distinto es el estudio del caos cuántico , mediante el cual se intenta cuantificar sistemas como clásicamente caóticos, ergódicos o mixtos. [ cita requerida ] Los resultados obtenidos no son muy distintos de los que se obtienen con el método del operador de transferencia. Por ejemplo, la cuantificación del gas de Boltzmann , es decir, un gas de partículas puntuales duras (elásticas) en una caja rectangular, revela que las funciones propias son fractales que llenan el espacio y ocupan toda la caja, y que los valores propios de energía están muy poco espaciados y tienen un espectro "casi continuo" (para un número finito de partículas en una caja, el espectro debe ser, necesariamente, discreto). Si las condiciones iniciales son tales que todas las partículas están confinadas en un lado de la caja, el sistema evoluciona muy rápidamente hacia uno en el que las partículas llenan toda la caja. Incluso cuando todas las partículas están inicialmente en un lado de la caja, sus funciones de onda, de hecho, impregnan toda la caja: interfieren constructivamente en un lado e interfieren destructivamente en el otro. La irreversibilidad se argumenta entonces señalando que es "casi imposible" que las funciones de onda se dispongan "accidentalmente" en algún estado improbable: tales disposiciones son un conjunto de medida cero . Debido a que las funciones propias son fractales, gran parte del lenguaje y la maquinaria de la entropía y la mecánica estadística se pueden importar para discutir y argumentar el caso cuántico. [ cita requerida ]
Algunos procesos que involucran partículas de alta energía y están gobernados por la fuerza débil (como la desintegración del mesón K ) desafían la simetría entre las direcciones del tiempo. Sin embargo, todos los procesos físicos conocidos sí conservan una simetría más complicada ( simetría CPT ), y por lo tanto no están relacionados con la segunda ley de la termodinámica, o con la experiencia cotidiana de la flecha del tiempo. Una excepción notable es el colapso de la función de onda en la mecánica cuántica , un proceso irreversible que se considera real (según la interpretación de Copenhague ) o solo aparente (según la interpretación de los muchos mundos de la mecánica cuántica). En cualquier caso, el colapso de la función de onda siempre sigue a la decoherencia cuántica , un proceso que se entiende como resultado de la segunda ley de la termodinámica.
El universo se encontraba en un estado uniforme y de alta densidad en sus primeras etapas, poco después del Big Bang. El gas caliente en el universo primitivo estaba cerca del equilibrio termodinámico (véase el problema del horizonte ); en los sistemas donde la gravitación desempeña un papel importante, este es un estado de baja entropía, debido a la capacidad térmica negativa de dichos sistemas (esto es al contrario de los sistemas no gravitacionales donde el equilibrio termodinámico es un estado de máxima entropía). Además, debido a su pequeño volumen en comparación con épocas futuras, la entropía era incluso menor a medida que la expansión del gas aumentaba su entropía. Por lo tanto, se puede considerar que el universo primitivo estaba altamente ordenado. Nótese que la uniformidad de este estado primitivo cercano al equilibrio ha sido explicada por la teoría de la inflación cósmica .
Según esta teoría, el universo (o, mejor dicho, su parte accesible, un radio de 46 mil millones de años luz alrededor de la Tierra) evolucionó a partir de un volumen diminuto y totalmente uniforme (una porción de un universo mucho más grande), que se expandió enormemente; por lo tanto, estaba altamente ordenado. Luego, se crearon fluctuaciones mediante procesos cuánticos relacionados con su expansión, de una manera que se supone es tal que estas fluctuaciones pasaron por una decoherencia cuántica, de modo que se volvieron incorrelagadas para cualquier uso práctico. Se supone que esto da las condiciones iniciales deseadas necesarias para la Segunda Ley de la Termodinámica; diferentes estados decoherentes finalmente evolucionaron a diferentes disposiciones específicas de galaxias y estrellas.
El universo es aparentemente un universo abierto , de modo que su expansión nunca terminará, pero es un experimento mental interesante imaginar qué habría sucedido si el universo hubiera sido cerrado . En tal caso, su expansión se detendría en un momento determinado en el futuro lejano, y luego comenzaría a contraerse. Además, un universo cerrado es finito. No está claro qué sucedería con la segunda ley de la termodinámica en tal caso. Se podrían imaginar al menos dos escenarios diferentes, aunque de hecho solo el primero es plausible, ya que el otro requiere una evolución cósmica muy suave, contrariamente a lo que se observa:
En el primer escenario, más consensuado, la diferencia entre el estado inicial y el estado final del universo es la responsable de la flecha termodinámica del tiempo, que es independiente de la flecha cosmológica del tiempo.
... se demuestra que para que haya una evolución global de la entropía hasta su valor máximo... es necesario y suficiente que el sistema tenga una propiedad conocida como exactitud. ... estos criterios sugieren que todas las leyes físicas formuladas actualmente pueden no estar en la base del comportamiento termodinámico que observamos todos los días de nuestra vida. (página xi)