Función exponencial

Función matemática, denotada exp(x) o e^x

Funciones exponenciales con bases 2 y 1/2

En matemáticas , la función exponencial es la única función real que asigna cero a uno y tiene una derivada igual a su valor. La exponencial de una variable se denota ${\displaystyle x}$ como o , ${\displaystyle \exp x}$y las dos notaciones se usan indistintamente. Se llama exponencial porque su argumento puede verse como un exponente al que se eleva un número constante e ≈ 2,718 , la base. Existen ${\displaystyle e^{x}}$ otras definiciones de la función exponencial, que son todas equivalentes aunque de naturaleza muy diferente.

La función exponencial convierte sumas en productos: asigna la identidad aditiva 0 a la identidad multiplicativa 1 , y el exponente de una suma es igual al producto de exponenciales separados, ⁠ ⁠ ${\displaystyle \exp(x+y)=\exp x\cdot \exp y}$ . Su función inversa , el logaritmo natural , ⁠ ⁠ ${\displaystyle \ln }$ o ⁠ ⁠ ${\displaystyle \log }$ , convierte productos en sumas: ⁠ ⁠ ${\displaystyle \ln(x\cdot y)=\ln x+\ln y}$ .

Otras funciones de la forma general ⁠ ⁠ ${\displaystyle f(x)=b^{x}}$ , con base ⁠ ⁠ ${\displaystyle b}$ , también se denominan comúnmente funciones exponenciales , y comparten la propiedad de convertir la suma en multiplicación, ⁠ ⁠ ${\displaystyle b^{x+y}=b^{x}\cdot b^{y}}$ . Cuando estos dos significados pueden confundirse, la función exponencial de base ⁠ ⁠ ${\displaystyle e}$ se denomina ocasionalmente función exponencial natural , que coincide con el nombre de logaritmo natural . La generalización de la notación exponencial estándar ⁠ ⁠ ${\displaystyle b^{x}}$ a números reales arbitrarios como exponentes, generalmente se define formalmente en términos de las funciones exponencial y logaritmo natural, como ⁠ ⁠ ${\displaystyle b^{x}=\exp(x\cdot \ln b)}$ . La base "natural" ⁠ ⁠ ${\displaystyle e=\exp 1}$ es la única base que satisface el criterio de que la derivada de la función exponencial es igual a su valor, ⁠ ⁠ ${\displaystyle {\tfrac {d}{dx}}e^{x}=e^{x}}$ , lo que simplifica las definiciones y elimina constantes extrañas cuando se utilizan funciones exponenciales en cálculo .

Las cantidades que cambian con el tiempo en proporción a su valor, por ejemplo el saldo de una cuenta bancaria que genera interés compuesto , el tamaño de una población bacteriana, la temperatura de un objeto en relación con su entorno o la cantidad de una sustancia radiactiva , se pueden modelar utilizando funciones de la forma ⁠ ⁠ ${\displaystyle y(t)=ae^{ct}}$ , también llamadas a veces funciones exponenciales ; estas cantidades experimentan un crecimiento exponencial si ⁠ ⁠ ${\displaystyle c}$ es positivo o una desintegración exponencial si ⁠ ⁠ ${\displaystyle c}$ es negativo.

La función exponencial se puede generalizar para aceptar un número complejo como argumento. Esto revela una relación entre la multiplicación de números complejos y la rotación en el plano euclidiano , la fórmula de Euler : la ${\displaystyle \exp i\theta =\cos \theta +i\sin \theta }$ exponencial de un número imaginario es un ${\displaystyle i\theta }$ punto en el círculo unitario complejo en un ángulo con el ${\displaystyle \theta }$ eje real. Las identidades de la trigonometría se pueden traducir así en identidades que involucran exponenciales de cantidades imaginarias. La función compleja es una función conforme de una franja infinita del plano complejo ( que se repite periódicamente en la dirección imaginaria) sobre todo el plano complejo excepto . ${\displaystyle z\mapsto \exp z}$ ${\displaystyle -\pi <\operatorname {Im} z\leq \pi }$ ${\displaystyle 0}$

La función exponencial puede incluso generalizarse aún más para aceptar otros tipos de argumentos, como matrices y elementos de álgebras de Lie . Algunos textos antiguos se refieren a la función exponencial como el antilogaritmo . ^[1]

Gráfico

La gráfica de tiene pendiente positiva y aumenta más rápido a medida que x aumenta. ^[2] La gráfica siempre se encuentra por encima del eje x , pero se acerca arbitrariamente a él para valores negativos grandes de x ; por lo tanto, el eje x es una asíntota horizontal . La ecuación significa que la pendiente de la tangente a la gráfica en cada punto es igual a su altura (su coordenada y ) en ese punto. ${\displaystyle y=e^{x}}$ ${\displaystyle {\tfrac {d}{dx}}e^{x}=e^{x}}$

Definiciones y propiedades fundamentales

Existen varias definiciones diferentes de la función exponencial, todas ellas equivalentes, aunque de naturaleza muy diferente.

Una de las definiciones más simples es: La función exponencial es la única función diferenciable que es igual a su derivada , y toma el valor 1 para el valor 0 de su variable.

Esta definición "conceptual" requiere una prueba de unicidad y una prueba de existencia, pero permite una fácil derivación de las principales propiedades de la función exponencial.

Unicidad: Si ⁠ ⁠ ${\displaystyle f(x)}$ y ⁠ ⁠ ${\displaystyle g(x)}$ son dos funciones que satisfacen la definición anterior, entonces la derivada de ⁠ ⁠ ${\displaystyle f/g}$ es cero en todas partes según la regla del cociente . De ello se deduce que ⁠ ⁠ ${\displaystyle g(x)}$ es constante, y esta constante es 1 ya que ⁠ ⁠ ${\displaystyle f(0)=g(0)=1}$ .

La función exponencial es la función inversa del logaritmo natural . El teorema de la función inversa implica que el logaritmo natural tiene una función inversa, que satisface la definición anterior. Esta es una primera prueba de existencia. Por lo tanto, se tiene

${\displaystyle {\begin{aligned}\ln(\exp x)&=x\\\exp(\ln y)&=y\end{aligned}}}$

para cada número real y cada número real positivo ${\displaystyle x}$ ${\displaystyle y.}$

La función exponencial (en azul) y la suma de los primeros n + 1 términos de su serie de potencias (en rojo)

La función exponencial es la suma de una serie de potencias : ^{[3] [4]} donde es el factorial de n (el producto de los n primeros números enteros positivos). Esta serie es absolutamente convergente para cada uno según la prueba de la razón . Por lo tanto, la derivada de la suma se puede calcular mediante la derivación término por término, y esto demuestra que la suma de la serie satisface la definición anterior. Esta es una segunda prueba de existencia y muestra, como subproducto, que la función exponencial es en todas partes la suma de su serie de Maclaurin . $${\displaystyle {\begin{aligned}\exp(x)&=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}},\end{aligned}}}$$ ${\displaystyle n!}$ ${\displaystyle x}$

La exponencial satisface la ecuación funcional: Esto resulta de la unicidad y del hecho de que la función satisface la definición anterior. Se puede demostrar que una función que satisface esta ecuación funcional es la función exponencial si su derivada en 0 es 1 y la función es continua o monótona. $${\displaystyle \exp(x+y)=\exp(x)\cdot \exp(y).}$$ ${\displaystyle f(x)=\exp(x+y)/\exp(y)}$

Positividad: La función exponencial es positiva y monótonamente creciente . La última propiedad resulta de la primera, ya que la derivada es igual a la función. La positividad resulta para del hecho de que todos los términos de la serie anterior son positivos. Para esto resulta de la identidad funcional que implica ${\displaystyle x>0}$ ${\displaystyle x<0,}$ ${\displaystyle \exp(-x)=1/\exp(x).}$

Extensión de la exponenciación a bases reales positivas: Sea b un número real positivo. Siendo la función exponencial y el logaritmo natural la inversa cada uno del otro, se tiene Si n es un entero, la ecuación funcional del logaritmo implica Dado que la expresión más a la derecha está definida si n es cualquier número real, esto permite definir ⁠ ⁠ para cada número real positivo b y cada número real x : En particular, si b es el número de Euler se tiene (función inversa) y por tanto Esto muestra la equivalencia de las dos notaciones para la función exponencial. ${\displaystyle b=\exp(\ln b).}$ $${\displaystyle b^{n}=\exp(\ln b^{n})=\exp(n\ln b).}$$ ${\displaystyle b^{x}}$ $${\displaystyle b^{x}=\exp(x\ln b).}$$ ${\displaystyle e=\exp(1),}$ ${\displaystyle \ln e=1}$ $${\displaystyle e^{x}=\exp(x).}$$

La función exponencial es el límite ^{[5] [4]} donde toma solo valores enteros (de lo contrario, la exponenciación requeriría que se definiera la función exponencial). Por continuidad del logaritmo, esto se puede demostrar tomando logaritmos y demostrando por ejemplo con el teorema de Taylor . $${\displaystyle \exp(x)=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n},}$$ ${\displaystyle n}$ $${\displaystyle x=\lim _{n\to \infty }\ln \left(1+{\frac {x}{n}}\right)^{n}=\lim _{n\to \infty }n\ln \left(1+{\frac {x}{n}}\right),}$$

Funciones exponenciales generales

La función exponencial a veces se denomina función exponencial natural para distinguirla de las otras funciones exponenciales. El estudio de cualquier función exponencial se puede reducir fácilmente al de la función exponencial natural, ya que por definición, para b positivo , Como funciones de una variable real, las funciones exponenciales se caracterizan únicamente por el hecho de que la derivada de dicha función es directamente proporcional al valor de la función. La constante de proporcionalidad de esta relación es el logaritmo natural de la base b : Sea un coeficiente positivo. Para , la función es creciente (como se representa para b = e y b = 2 ), porque hace que la derivada sea siempre positiva y describe un crecimiento exponencial. Para , la función es decreciente (como se representa para b = ⁠ ${\displaystyle f(x)=e^{x}}$ $${\displaystyle a\,b^{x}\mathrel {\stackrel {\text{def}}{=}} a\,e^{x\ln b}}$$ $${\displaystyle {\frac {d}{dx}}a\,b^{x}={\frac {d}{dx}}a\,e^{x\ln(b)}=a\,e^{x\ln(b)}\ln(b)=a\,b^{x}\ln(b).}$$ ${\displaystyle a>0}$ ${\displaystyle b>1}$ ${\displaystyle a\,b^{x}}$ ${\displaystyle \ln b>0}$ ${\displaystyle 0<b<1}$1/2⁠ ), y describe el decaimiento exponencial. Para b = 1 , la función es constante.

El número de Euler e = 2,71828... ^[6] es la única base para la que la constante de proporcionalidad es 1, ya que , de modo que la función es su propia derivada: ${\displaystyle \ln(e)=1}$ $${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}\ln(e)=e^{x}.}$$

Esta función, también denotada como , se llama "función exponencial natural", ^{[7] [8]} o simplemente "la función exponencial", denotada como La primera notación se usa comúnmente para exponentes más simples, mientras que la última se prefiere cuando el exponente es más complicado y más difícil de leer en una fuente pequeña. Dado que cualquier función exponencial se puede escribir en términos de la exponencial natural, es computacional y conceptualmente conveniente reducir el estudio de las funciones exponenciales a esta en particular. ${\displaystyle \exp(x)}$ $${\displaystyle x\mapsto e^{x}\quad {\text{or}}\quad x\mapsto \exp(x).}$$ ${\displaystyle f(x)=a\,b^{x}}$

Para los números reales , una función de la forma también es una función exponencial: ${\displaystyle c,d}$ ${\displaystyle f(x)=ab^{cx+d}}$ $${\displaystyle ab^{cx+d}=\left(ab^{d}\right)\left(b^{c}\right)^{x}=\left(ab^{d}\right)e^{xc\ln b}.}$$

Descripción general

La curva roja es la función exponencial. Las líneas horizontales negras muestran dónde se cruza con las líneas verticales verdes.

La función exponencial surge siempre que una cantidad crece o decae a una tasa proporcional a su valor actual. Una de esas situaciones es el interés compuesto continuo y, de hecho, fue esta observación la que llevó a Jacob Bernoulli en 1683 ^[9] al número que hoy conocemos como e . Más tarde, en 1697, Johann Bernoulli estudió el cálculo de la función exponencial. ^[9] $${\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}$$

Si un monto principal de 1 genera intereses a una tasa anual de x compuesta mensualmente, entonces el interés ganado cada mes esincógnita/12⁠ veces el valor actual, por lo que cada mes el valor total se multiplica por (1 + ⁠incógnita/12⁠ ) ​​, y el valor al final del año es (1 + ⁠incógnita/12⁠ ) ^​​12 . Si en cambio el interés se capitaliza diariamente, esto se convierte en (1 + ⁠incógnita/365⁠ ) ^​​365 . Dejar que el número de intervalos de tiempo por año crezca sin límite conduce a la definición límite de la función exponencial, dada por primera vez por Leonhard Euler . ^[5] Esta es una de varias caracterizaciones de la función exponencial ; otras involucran series o ecuaciones diferenciales . $${\displaystyle \exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}$$

De cualquiera de estas definiciones se puede demostrar que e ^{− x} es el recíproco de e ^x . Por ejemplo, de la definición de ecuación diferencial, e ^x e ^{− x} = 1 cuando x = 0 y su derivada usando la regla del producto es e ^x e ^{− x} − e ^x e ^{− x} = 0 para todo x , por lo que e ^x e ^{− x} = 1 para todo x .

A partir de cualquiera de estas definiciones se puede demostrar que la función exponencial obedece a la identidad de exponenciación básica . Por ejemplo, a partir de la definición de serie de potencias, desarrollada por el teorema del binomio , Esto justifica la notación exponencial e ^x para exp x . $${\displaystyle \exp(x+y)=\sum _{n=0}^{\infty }{\frac {(x+y)^{n}}{n!}}=\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {n!}{k!(n-k)!}}{\frac {x^{k}y^{n-k}}{n!}}=\sum _{k=0}^{\infty }\sum _{\ell =0}^{\infty }{\frac {x^{k}y^{\ell }}{k!\ell !}}=\exp x\cdot \exp y\,.}$$

La derivada (tasa de cambio) de la función exponencial es la función exponencial en sí misma. En términos más generales, una función con una tasa de cambio proporcional a la función misma se puede expresar en términos de la función exponencial. Esta propiedad de la derivada conduce a un crecimiento exponencial o a un decrecimiento exponencial.

La función exponencial se extiende a una función completa en el plano complejo . La fórmula de Euler relaciona sus valores en argumentos puramente imaginarios con funciones trigonométricas . La función exponencial también tiene análogos para los cuales el argumento es una matriz , o incluso un elemento de un álgebra de Banach o un álgebra de Lie .

Derivadas y ecuaciones diferenciales

La derivada de la función exponencial es igual al valor de la función. Desde cualquier punto P de la curva (azul), tracemos una línea tangente (roja) y una línea vertical (verde) con altura h , formando un triángulo rectángulo con base b en el eje x . Como la pendiente de la línea tangente roja (la derivada) en P es igual al cociente entre la altura del triángulo y la base del triángulo (elevación sobre recorrido), y la derivada es igual al valor de la función, h debe ser igual al cociente entre h y b . Por lo tanto, la base b siempre debe ser 1.

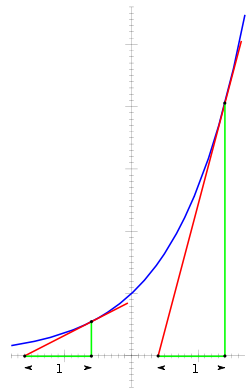
La importancia de la función exponencial en las matemáticas y las ciencias se debe principalmente a su propiedad de ser la única función que es igual a su derivada y es igual a 1 cuando x = 0. Es decir, $${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}\quad {\text{and}}\quad e^{0}=1.}$$

Las funciones de la forma ae ^x para una constante a son las únicas funciones que son iguales a su derivada (según el teorema de Picard-Lindelöf ). Otras formas de decir lo mismo son:

• La pendiente de la gráfica en cualquier punto es la altura de la función en ese punto.
• La tasa de aumento de la función en x es igual al valor de la función en x .
• La función resuelve la ecuación diferencial y ′ = y .
• exp es un punto fijo de la derivada como operador lineal en el espacio funcional .

Si la tasa de crecimiento o decaimiento de una variable es proporcional a su tamaño (como es el caso del crecimiento ilimitado de una población, ver la catástrofe maltusiana ), el interés compuesto continuo o el decaimiento radiactivo ), entonces la variable puede escribirse como una constante multiplicada por una función exponencial del tiempo.

De manera más general, para cualquier constante real k , una función f : R → R satisface si y solo si para alguna constante a . La constante k se denomina constante de decaimiento , constante de desintegración , ^[10] constante de velocidad , ^[11] o constante de transformación . ^[12] ${\displaystyle f'=kf}$ ${\displaystyle f(x)=ae^{kx}}$

Además, para cualquier función diferenciable f , encontramos, por la regla de la cadena : $${\displaystyle {\frac {d}{dx}}e^{f(x)}=f'(x)\,e^{f(x)}.}$$

Fracciones continuas paraex​

Una fracción continua para e ^x se puede obtener mediante una identidad de Euler : $${\displaystyle e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-\ddots }}}}}}}}}$$

La siguiente fracción continua generalizada para e ^z converge más rápidamente: ^[13] $${\displaystyle e^{z}=1+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{10+{\cfrac {z^{2}}{14+\ddots }}}}}}}}}$$

o, aplicando la sustitución z = ⁠incógnita/y⁠ : con un caso especial para z = 2 : $${\displaystyle e^{\frac {x}{y}}=1+{\cfrac {2x}{2y-x+{\cfrac {x^{2}}{6y+{\cfrac {x^{2}}{10y+{\cfrac {x^{2}}{14y+\ddots }}}}}}}}}$$ $${\displaystyle e^{2}=1+{\cfrac {4}{0+{\cfrac {2^{2}}{6+{\cfrac {2^{2}}{10+{\cfrac {2^{2}}{14+\ddots \,}}}}}}}}=7+{\cfrac {2}{5+{\cfrac {1}{7+{\cfrac {1}{9+{\cfrac {1}{11+\ddots \,}}}}}}}}}$$

Esta fórmula también converge, aunque más lentamente, para z > 2 . Por ejemplo: $${\displaystyle e^{3}=1+{\cfrac {6}{-1+{\cfrac {3^{2}}{6+{\cfrac {3^{2}}{10+{\cfrac {3^{2}}{14+\ddots \,}}}}}}}}=13+{\cfrac {54}{7+{\cfrac {9}{14+{\cfrac {9}{18+{\cfrac {9}{22+\ddots \,}}}}}}}}}$$

Plano complejo

La función exponencial e^z graficada en el plano complejo desde -2-2i hasta 2+2i

Un gráfico complejo de , con el argumento representado por un tono variable. La transición de colores oscuros a claros muestra que aumenta solo hacia la derecha. Las bandas horizontales periódicas correspondientes al mismo tono indican que es periódica en la parte imaginaria de . ${\displaystyle z\mapsto \exp z}$ ${\displaystyle \operatorname {Arg} \exp z}$ ${\displaystyle \left|\exp z\right|}$ ${\displaystyle z\mapsto \exp z}$ ${\displaystyle z}$

Como en el caso real , la función exponencial se puede definir en el plano complejo en varias formas equivalentes.

La definición más común de la función exponencial compleja es paralela a la definición de serie de potencias para argumentos reales, donde la variable real se reemplaza por una compleja: $${\displaystyle \exp z:=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}}$$

Alternativamente, la función exponencial compleja puede definirse modelando la definición del límite para argumentos reales, pero con la variable real reemplazada por una compleja: $${\displaystyle \exp z:=\lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}}$$

Para la definición de serie de potencias, la multiplicación término por término de dos copias de esta serie de potencias en el sentido de Cauchy , permitida por el teorema de Mertens , muestra que la propiedad multiplicativa definitoria de las funciones exponenciales continúa siendo válida para todos los argumentos complejos: $${\displaystyle \exp(w+z)=\exp w\exp z{\text{ for all }}w,z\in \mathbb {C} }$$

La definición de la función exponencial compleja conduce a su vez a las definiciones apropiadas que extienden las funciones trigonométricas a argumentos complejos.

En particular, cuando z = it ( t real), la definición de la serie produce la expansión $${\displaystyle \exp(it)=\left(1-{\frac {t^{2}}{2!}}+{\frac {t^{4}}{4!}}-{\frac {t^{6}}{6!}}+\cdots \right)+i\left(t-{\frac {t^{3}}{3!}}+{\frac {t^{5}}{5!}}-{\frac {t^{7}}{7!}}+\cdots \right).}$$

En este desarrollo, la reorganización de los términos en partes reales e imaginarias se justifica por la convergencia absoluta de la serie. Las partes reales e imaginarias de la expresión anterior corresponden de hecho a los desarrollos en serie de cos t y sen t , respectivamente.

Esta correspondencia proporciona una motivación para definir coseno y seno para todos los argumentos complejos en términos de y la serie de potencia equivalente: ^[14] ${\displaystyle \exp(\pm iz)}$ $${\displaystyle {\begin{aligned}&\cos z:={\frac {\exp(iz)+\exp(-iz)}{2}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k}}{(2k)!}},\\[5pt]{\text{and }}\quad &\sin z:={\frac {\exp(iz)-\exp(-iz)}{2i}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k+1}}{(2k+1)!}}\end{aligned}}}$$

a pesar de ${\textstyle z\in \mathbb {C} .}$

Las funciones exp , cos y sen así definidas tienen radios de convergencia infinitos según la prueba de la razón y, por lo tanto, son funciones enteras (es decir, holomorfas en ). El rango de la función exponencial es , mientras que los rangos de las funciones complejas seno y coseno son ambos en su totalidad, de acuerdo con el teorema de Picard , que afirma que el rango de una función entera no constante es todo , o excluyendo un valor lagunar . ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} \setminus \{0\}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

Estas definiciones de las funciones exponenciales y trigonométricas conducen trivialmente a la fórmula de Euler : $${\displaystyle \exp(iz)=\cos z+i\sin z{\text{ for all }}z\in \mathbb {C} .}$$

Podríamos definir alternativamente la función exponencial compleja en base a esta relación. Si z = x + iy , donde x e y son ambos reales, entonces podríamos definir su exponencial como donde exp , cos y sin en el lado derecho del signo de definición deben interpretarse como funciones de una variable real, previamente definida por otros medios. ^[15] $${\displaystyle \exp z=\exp(x+iy):=(\exp x)(\cos y+i\sin y)}$$

Para , la relación se cumple, de modo que para los reales y asigna la línea real (mod 2 π ) al círculo unitario en el plano complejo. Además, yendo de a , la curva definida por traza un segmento del círculo unitario de longitud que comienza en z = 1 en el plano complejo y va en sentido antihorario. Con base en estas observaciones y en el hecho de que la medida de un ángulo en radianes es la longitud del arco en el círculo unitario subtendido por el ángulo, es fácil ver que, restringido a argumentos reales, las funciones seno y coseno como se definieron anteriormente coinciden con las funciones seno y coseno como se introdujeron en las matemáticas elementales a través de nociones geométricas. ${\displaystyle t\in \mathbb {R} }$ ${\displaystyle {\overline {\exp(it)}}=\exp(-it)}$ ${\displaystyle \left|\exp(it)\right|=1}$ ${\displaystyle t}$ ${\displaystyle t\mapsto \exp(it)}$ ${\displaystyle t=0}$ ${\displaystyle t=t_{0}}$ ${\displaystyle \gamma (t)=\exp(it)}$ $${\displaystyle \int _{0}^{t_{0}}|\gamma '(t)|\,dt=\int _{0}^{t_{0}}|i\exp(it)|\,dt=t_{0},}$$

La función exponencial compleja es periódica con período 2 πi y es válida para todo . ${\displaystyle \exp(z+2\pi ik)=\exp z}$ ${\displaystyle z\in \mathbb {C} ,k\in \mathbb {Z} }$

Cuando su dominio se extiende desde la línea real al plano complejo, la función exponencial conserva las siguientes propiedades: $${\displaystyle {\begin{aligned}&e^{z+w}=e^{z}e^{w}\,\\[5pt]&e^{0}=1\,\\[5pt]&e^{z}\neq 0\\[5pt]&{\frac {d}{dz}}e^{z}=e^{z}\\[5pt]&\left(e^{z}\right)^{n}=e^{nz},n\in \mathbb {Z} \end{aligned}}}$$

a pesar de ${\textstyle w,z\in \mathbb {C} .}$

Extender el logaritmo natural a argumentos complejos produce el logaritmo complejo log z , que es una función multivalor .

Podemos definir entonces una exponenciación más general: para todos los números complejos z y w . Esta también es una función multivaluada, incluso cuando z es real. Esta distinción es problemática, ya que las funciones multivaluadas log z y z ^w se confunden fácilmente con sus equivalentes univaluados cuando se sustituye z por un número real . La regla sobre la multiplicación de exponentes para el caso de números reales positivos debe modificarse en un contexto multivaluado: $${\displaystyle z^{w}=e^{w\log z}}$$

( y ^z )^el
≠ e ^zw , sino ( e ^z )^el
= e ^{( z + 2 niπ ) w} multivaluado sobre números enteros n

Consulte Falla de identidades de potencia y logaritmo para obtener más información sobre los problemas con la combinación de potencias.

La función exponencial convierte cualquier línea en el plano complejo en una espiral logarítmica en el plano complejo con centro en el origen . Existen dos casos especiales: cuando la línea original es paralela al eje real, la espiral resultante nunca se cierra sobre sí misma; cuando la línea original es paralela al eje imaginario, la espiral resultante es un círculo de cierto radio.

• Gráficos 3D de la parte real, la parte imaginaria y el módulo de la función exponencial
• 
  z ⁼ Re( ex ^{+ iy} )
• 
  z ⁼ Im( ex ^{+ iy} )
• 
  z = | e ^{x + iy} |

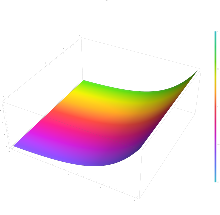
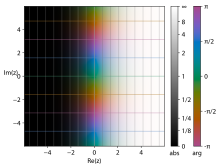
Considerando la función exponencial compleja como una función que involucra cuatro variables reales: la gráfica de la función exponencial es una superficie bidimensional que se curva a través de cuatro dimensiones. $${\displaystyle v+iw=\exp(x+iy)}$$

Comenzando con una porción del dominio codificada por colores, las siguientes son representaciones del gráfico proyectado de diversas formas en dos o tres dimensiones. ${\displaystyle xy}$

• Gráficas de la función exponencial compleja
• 
  Clave del tablero de ajedrez:
  ${\displaystyle x>0:\;{\text{green}}}$
  ${\displaystyle x<0:\;{\text{red}}}$
  ${\displaystyle y>0:\;{\text{yellow}}}$
  ${\displaystyle y<0:\;{\text{blue}}}$
• 
  Proyección sobre el plano complejo de rango (V/W). Compárese con la siguiente imagen en perspectiva.
• 
  Proyección en las dimensiones , , y , produciendo una forma de cuerno ensanchado o embudo (imaginada como una imagen en perspectiva 2D) ${\displaystyle x}$ ${\displaystyle v}$ ${\displaystyle w}$
• 
  Proyección en las dimensiones , , y , produciendo una forma espiral ( rango ampliado a ±2 π , nuevamente como imagen en perspectiva 2-D) ${\displaystyle y}$ ${\displaystyle v}$ ${\displaystyle w}$ ${\displaystyle y}$

La segunda imagen muestra cómo el plano complejo de dominio se asigna al plano complejo de rango:

• El cero se asigna a 1
• El eje real se asigna al eje real positivo. ${\displaystyle x}$ ${\displaystyle v}$
• El eje imaginario se envuelve alrededor del círculo unitario a una velocidad angular constante. ${\displaystyle y}$
• Los valores con partes reales negativas se asignan dentro del círculo unitario.
• Los valores con partes reales positivas se asignan fuera del círculo unitario.
• Los valores con una parte real constante se asignan a círculos centrados en cero.
• Los valores con una parte imaginaria constante se asignan a rayos que se extienden desde cero.

La tercera y cuarta imágenes muestran cómo el gráfico de la segunda imagen se extiende a una de las otras dos dimensiones que no se muestran en la segunda imagen.

La tercera imagen muestra el gráfico extendido a lo largo del eje real. Muestra que el gráfico es una superficie de revolución alrededor del eje del gráfico de la función exponencial real, lo que produce una forma de cuerno o embudo. ${\displaystyle x}$ ${\displaystyle x}$

La cuarta imagen muestra el gráfico extendido a lo largo del eje imaginario. Muestra que la superficie del gráfico para valores positivos y negativos en realidad no se encuentra a lo largo del eje real negativo, sino que forma una superficie espiral alrededor del eje. Debido a que sus valores se han extendido a ±2 π , esta imagen también representa mejor la periodicidad 2π en el valor imaginario. ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle v}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle y}$

Cálculo deun bdonde ambosaybson complejos

La exponenciación compleja a ^b se puede definir convirtiendo a a coordenadas polares y utilizando la identidad e ^{b ln a} = a ^b : $${\displaystyle a^{b}=e^{b\ln a}=e^{b\ln |a|+ib\theta }}$$

siendo un argumento de . Sin embargo, cuando b no es un entero, esta función es multivaluada , porque θ no es única (ver Exponenciación § Fallo de identidades de potencia y logaritmo ). El cociente no se puede definir de esta manera ya que no está definido. La elección del valor principal de satisface , y esto también define el valor principal de . ${\displaystyle \theta }$ ${\displaystyle a}$ ${\displaystyle 0^{b}}$ ${\displaystyle \log 0}$ ${\displaystyle a^{b}}$ ${\displaystyle -\pi <\theta \leq \pi }$ ${\displaystyle \log a}$

Funciones de potencia y función exponencial con base compleja

Dado un número complejo y una vez que hemos definido el valor principal de , podemos definir las funciones univaluadas (conocidas como la función potencia ) y , que es similar a la función exponencial pero la base puede ser un número complejo. Si no es un entero, entonces tiene discontinuidades en los reales negativos, ya que y esto se deduce del hecho de que la función logaritmo compleja es discontinua en los reales negativos . La serie de Maclaurin de la función está dada por Esto se conoce como la serie binomial . Además, si tiene una parte real positiva, entonces la serie converge absolutamente para , y el límite de también existe como dentro del círculo unitario y es igual a , por lo que también podemos definir . Si tiene una parte real no positiva y luego la serie diverge, por lo que permanece indefinida. La expresión se deja indefinida porque es una forma indeterminada en cálculo . La función definida aquí es holomorfa en todas partes en el plano complejo y, por lo tanto, es entera . La serie de Maclaurin de está dada por ${\displaystyle b}$ ${\displaystyle z^{b}}$ ${\displaystyle f(z)=z^{b}}$ ${\displaystyle g(z)=b^{z}}$ ${\displaystyle b}$ ${\displaystyle f}$ ${\displaystyle f(z)=e^{b\ln z}}$ ${\displaystyle f(1+z)}$ $${\displaystyle f(1+z)=\sum _{k=0}^{\infty }{\frac {b(b-1)...(b-k+1)}{k!}}z^{k}=1+bz+{\frac {b(b-1)}{2}}z^{2}+\cdots ,\qquad |z|<1.}$$ ${\displaystyle b}$ ${\displaystyle z=-1}$ ${\displaystyle f(1+z)}$ ${\displaystyle z\to -1}$ ${\displaystyle 0}$ ${\displaystyle 0^{b}:=\lim _{z\to -1}f(1+z)=0}$ ${\displaystyle b}$ ${\displaystyle b\neq 0}$ ${\displaystyle 0^{b}}$ ${\displaystyle 0^{0}}$ ${\displaystyle g}$ ${\displaystyle g}$ $${\displaystyle g(z)=b^{z}=e^{z\ln b}=\sum _{k=0}^{\infty }{\frac {(\log b)^{k}}{k!}}z^{k}.}$$

Matrices y álgebras de Banach

La definición de serie de potencias de la función exponencial tiene sentido para matrices cuadradas (para las cuales la función se llama exponencial matricial ) y, de manera más general, en cualquier álgebra de Banach unitaria B. En este contexto, e ⁰ = 1 , y e ^x es invertible con e ^{− x} inverso para cualquier x en B. Si xy = yx , entonces e ^{x + y} = e ^x e ^y , pero esta identidad puede fallar para x e y no conmutativos .

Algunas definiciones alternativas conducen a la misma función. Por ejemplo, e ^x puede definirse como $${\displaystyle \lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.}$$

O e ^x se puede definir como f _x (1) , donde f _x  : R → B es la solución de la ecuación diferencial ⁠dfx_​/es⁠ ( t ) = x  f _x ( t ) , con condición inicial f _x (0) = 1 ; se sigue que f _x ( t ) = e ^tx para cada t en R .

Álgebras de Lie

Dado un grupo de Lie G y su álgebra de Lie asociada , la función exponencial es una función ↦ G que satisface propiedades similares. De hecho, dado que R es el álgebra de Lie del grupo de Lie de todos los números reales positivos bajo multiplicación, la función exponencial ordinaria para argumentos reales es un caso especial de la situación del álgebra de Lie. De manera similar, dado que el grupo de Lie GL( n , R ) de matrices invertibles n × n tiene como álgebra de Lie M( n , R ) , el espacio de todas las matrices n × n , la función exponencial para matrices cuadradas es un caso especial de la función exponencial del álgebra de Lie. ${\displaystyle {\mathfrak {g}}}$ ${\displaystyle {\mathfrak {g}}}$

La identidad puede fallar para los elementos del álgebra de Lie x e y que no conmutan; la fórmula de Baker–Campbell–Hausdorff proporciona los términos de corrección necesarios. ${\displaystyle \exp(x+y)=\exp(x)\exp(y)}$

Trascendencia

La función e ^z no está en el anillo de funciones racionales : no es el cociente de dos polinomios con coeficientes complejos. ${\displaystyle \mathbb {C} (z)}$

Si a ₁ , ..., a _n son números complejos distintos, entonces e ^{a ₁ z} , ..., e ^{a _n z} son linealmente independientes sobre , y por lo tanto e ^z es trascendental sobre . ${\displaystyle \mathbb {C} (z)}$ ${\displaystyle \mathbb {C} (z)}$

Cálculo

La definición de la serie de Taylor anterior es generalmente eficiente para calcular (una aproximación de) . Sin embargo, al calcular cerca del argumento , el resultado será cercano a 1, y calcular el valor de la diferencia con aritmética de punto flotante puede llevar a la pérdida de (posiblemente todas) las cifras significativas , lo que produce un gran error relativo, posiblemente incluso un resultado sin sentido. ${\displaystyle e^{x}}$ ${\displaystyle x=0}$ ${\displaystyle e^{x}-1}$

Siguiendo una propuesta de William Kahan , puede ser útil tener una rutina dedicada, a menudo llamada expm1, que calcule e ^x − 1 directamente, evitando el cálculo de e ^x . Por ejemplo, se puede utilizar la serie de Taylor: $${\displaystyle e^{x}-1=x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots +{\frac {x^{n}}{n!}}+\cdots .}$$

Esto se implementó por primera vez en 1979 en la calculadora Hewlett-Packard HP-41C y lo proporcionan varias calculadoras, ^{[16] [17]} sistemas operativos (por ejemplo, Berkeley UNIX 4.3BSD ^[18] ), sistemas de álgebra computacional y lenguajes de programación (por ejemplo, C99 ). ^[19]

Además de la base e , el estándar IEEE 754-2008 define funciones exponenciales similares cerca de 0 para bases 2 y 10: y . ${\displaystyle 2^{x}-1}$ ${\displaystyle 10^{x}-1}$

Se ha utilizado un enfoque similar para el logaritmo (véase lnp1 ). ^{[nb 1]}

Una identidad en términos de la tangente hiperbólica , proporciona un valor de alta precisión para valores pequeños de x en sistemas que no implementan expm1( x ) . $${\displaystyle \operatorname {expm1} (x)=e^{x}-1={\frac {2\tanh(x/2)}{1-\tanh(x/2)}},}$$

Véase también

• Portal de matemáticas

• Exponencial de Carlitz , un análogo característico de p
• Función exponencial doble  – Función exponencial de una función exponencial
• Campo exponencial  – Campo matemático con una operación extra
• Función gaussiana
• Función semiexponencial , raíz cuadrada compositiva de una función exponencial
• Función Lambert W#Resolver ecuaciones  – Función multivalor en matemáticas: se utiliza para resolver ecuaciones exponenciales
• Lista de temas exponenciales
• Lista de integrales de funciones exponenciales
• Función Mittag-Leffler , una generalización de la función exponencial
• función exponencial p -ádica
• Tabla de Padé para funciones exponenciales – Aproximación de Padé de funciones exponenciales mediante una fracción de funciones polinómicas
• Factor de fase

Notas

1. Un enfoque similar para reducir los errores de redondeo de los cálculos para ciertos valores de entrada de funciones trigonométricas consiste en utilizar las funciones trigonométricas menos comunes versine , vercosine , coversine , covercosine , haversine , havercosine , hacoversine , hacovercosine , exsecant y excosecant .

Referencias

1. Converse, Henry Augustus; Durell, Fletcher (1911). Trigonometría plana y esférica. Serie matemática de Durell. CE Merrill Company. pág. 12. Uso inverso de una tabla de logaritmos; es decir, dado un logaritmo, encontrar el número correspondiente a él (llamado su antilogaritmo) ...[1]
2. "Referencia de funciones exponenciales". www.mathsisfun.com . Consultado el 28 de agosto de 2020 .
3. Rudin, Walter (1987). Análisis real y complejo (3.ª ed.). Nueva York: McGraw-Hill . p. 1. ISBN. 978-0-07-054234-1.
4. Weisstein, Eric W. "Función exponencial". mathworld.wolfram.com . Consultado el 28 de agosto de 2020 .
5. Maor, Eli . e: La historia de un número . p. 156.
6. Sloane, N. J. A. (ed.). "Secuencia A001113 (Expansión decimal de e)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
7. Goldstein, Larry Joel; Lay, David C.; Schneider, David I.; Asmar, Nakhle H. (2006). Cálculo breve y sus aplicaciones (11.ª ed.). Prentice–Hall. ISBN 978-0-13-191965-5.(467 páginas)
8. Courant; Robbins (1996). Stewart (ed.). ¿Qué son las matemáticas? Un enfoque elemental de las ideas y los métodos (2.ª edición revisada). Oxford University Press . p. 448. ISBN 978-0-13-191965-5Esta función exponencial natural es idéntica a su derivada. Esta es realmente la fuente de todas las propiedades de la función exponencial y la razón básica de su importancia en las aplicaciones...
9. O'Connor, John J.; Robertson, Edmund F. (septiembre de 2001). "El número e". Facultad de Matemáticas y Estadística . Universidad de St Andrews, Escocia . Consultado el 13 de junio de 2011 .
10. Serway, Raymond A.; Moses, Clement J.; Moyer, Curt A. (1989). Física moderna . Fort Worth: Harcourt Brace Jovanovich . pág. 384. ISBN. 0-03-004844-3.
11. Simmons, George F. (1972). Ecuaciones diferenciales con aplicaciones y notas históricas . Nueva York: McGraw-Hill . pág. 15. LCCN  75173716.
12. Enciclopedia de ciencia y tecnología de McGraw-Hill (10.ª edición). Nueva York: McGraw-Hill . 2007. ISBN 978-0-07-144143-8.
13. Lorentzen, L. ; Waadeland, H. (2008). "A.2.2 La función exponencial". Fracciones continuas . Atlantis Studies in Mathematics. Vol. 1. p. 268. doi :10.2991/978-94-91216-37-4. ISBN 978-94-91216-37-4.
14. Rudin, Walter (1976). Principios del análisis matemático. Nueva York: McGraw-Hill . pág. 182. ISBN. 978-0-07-054235-8.
15. Apostol, Tom M. (1974). Análisis matemático (2.ª ed.). Reading, Mass.: Addison Wesley . pp. 19. ISBN 978-0-201-00288-1.
16. HP 48G Series – Manual de referencia del usuario avanzado (AUR) (4.ª edición). Hewlett-Packard . Diciembre de 1994 [1993]. HP 00048-90136, 0-88698-01574-2 . Consultado el 6 de septiembre de 2015 .
17. Manual de referencia del usuario avanzado (AUR) de la calculadora gráfica HP 50g/49g+/48gII (2.ª ed.). Hewlett-Packard . 2009-07-14 [2005]. HP F2228-90010 . Consultado el 10 de octubre de 2015 .[2]
18. Beebe, Nelson HF (22 de agosto de 2017). "Capítulo 10.2. Exponencial cerca de cero". Manual de cálculo de funciones matemáticas: programación con la biblioteca de software portátil MathCW (1.ª edición). Salt Lake City, UT, EE. UU.: Springer International Publishing AG . pp. 273–282. doi :10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN  2017947446. S2CID  30244721. Berkeley UNIX 4.3BSD introdujo la función expm1() en 1987.
19. Beebe, Nelson HF (9 de julio de 2002). "Cálculo de expm1 = exp(x)−1" (PDF) . 1.00. Salt Lake City, Utah, EE. UU.: Departamento de Matemáticas, Centro de Computación Científica, Universidad de Utah . Consultado el 2 de noviembre de 2015 .

Enlaces externos

• "Función exponencial", Enciclopedia de matemáticas , EMS Press , 2001 [1994]