Categoría enriquecida

En la teoría de categorías , una rama de las matemáticas , una categoría enriquecida generaliza la idea de una categoría al reemplazar conjuntos hom con objetos de una categoría monoidal general . Está motivada por la observación de que, en muchas aplicaciones prácticas, el conjunto hom a menudo tiene una estructura adicional que debe respetarse, por ejemplo, la de ser un espacio vectorial de morfismos o un espacio topológico de morfismos. En una categoría enriquecida, el conjunto de morfismos (el conjunto hom) asociado con cada par de objetos se reemplaza por un objeto en alguna categoría monoidal fija de "objetos hom". Para emular la composición (asociativa) de morfismos en una categoría ordinaria, la categoría hom debe tener un medio para componer hom-objetos de manera asociativa: es decir, debe haber una operación binaria sobre los objetos que nos dé al menos la estructura de una categoría monoidal , aunque en algunos contextos la operación también puede necesitar ser conmutativa y quizás también tener un adjunto derecho (es decir, hacer que la categoría sea monoidal simétrica o incluso monoidal cerrada simétrica , respectivamente). ^{[ cita requerida ]}

La teoría de categorías enriquecida abarca, por tanto, dentro del mismo marco una amplia variedad de estructuras, entre ellas:

Categorías ordinarias en las que el conjunto hom lleva una estructura adicional más allá de ser un conjunto. Es decir, hay operaciones sobre morfismos o propiedades de los mismos que deben ser respetadas por la composición (por ejemplo, la existencia de 2-celdas entre morfismos y su composición horizontal en una 2-categoría , o la operación de adición sobre morfismos en una categoría abeliana ).
entidades de tipo categorial que no tienen en sí mismas ninguna noción de morfismo individual pero cuyos hom-objetos tienen aspectos compositivos similares (por ejemplo, preórdenes donde la regla de composición asegura la transitividad, o espacios métricos de Lawvere , donde los hom-objetos son distancias numéricas y la regla de composición proporciona la desigualdad triangular).

En el caso en que la categoría del objeto homónimo resulta ser la categoría de conjuntos con el producto cartesiano habitual, las definiciones de categoría enriquecida, funtor enriquecido, etc... se reducen a las definiciones originales de la teoría de categorías ordinaria.

Se dice que una categoría enriquecida con hom-objetos de la categoría monoidal M es una categoría enriquecida sobre M o una categoría enriquecida en M , o simplemente una M-categoría . Debido a la preferencia de Mac Lane por la letra V para referirse a la categoría monoidal, a las categorías enriquecidas también se las denomina en general V-categorías .

Definición

Sea $(M, \otimes, I, α, λ, ρ)$ una categoría monoidal . Entonces una categoría enriquecida C (alternativamente, en situaciones donde la elección de la categoría monoidal debe ser explícita, una categoría enriquecida sobre M , o M - categoría ), consiste en

una clase ob ( C ) de objetos de C ,
un objeto $C (a, b)$ de M para cada par de objetos a , b en C , utilizado para definir una flecha en C como una flecha en M , $f:a\rightarrow b$ $f:I\rightarrow C(a,b)$
una flecha $id a : I \to C (a, a)$ en M que designa una identidad para cada objeto a en C , y
una flecha $° abc : C (b, c) \otimes C (a, b) \to C (a, c)$ en M que designa una composición para cada triple de objetos a , b , c en C , utilizada para definir la composición de y en C como junto con tres diagramas de conmutación, que se analizan a continuación. $f:a\rightarrow b$ $g:b\rightarrow c$ $g\circ _{\textbf {C}}f={^{\circ }}_{abc}(g\otimes f)$

El primer diagrama expresa la asociatividad de la composición:

Es decir, el requisito de asociatividad ahora lo asume el asociador de la categoría monoidal M.

Para el caso de que M sea la categoría de conjuntos y $(\otimes, I, α, λ, ρ)$ sea la estructura monoidal $(\times, {•}, ...)$ dada por el producto cartesiano , el conjunto unipunto terminal y los isomorfismos canónicos que inducen, entonces cada $C (a, b)$ es un conjunto cuyos elementos pueden considerarse como "morfismos individuales" de C , mientras que °, ahora una función, define cómo se componen los morfismos consecutivos. En este caso, cada camino que conduce a $C (a, d)$ en el primer diagrama corresponde a una de las dos formas de componer tres morfismos individuales consecutivos $a \to b \to c \to d$ , es decir, elementos de $C (a, b)$ , $C (b, c)$ y $C (c, d)$ . La conmutatividad del diagrama es entonces simplemente la afirmación de que ambos órdenes de composición dan el mismo resultado, exactamente como se requiere para las categorías ordinarias.

Lo novedoso aquí es que lo anterior expresa el requisito de asociatividad sin ninguna referencia explícita a morfismos individuales en la categoría enriquecida C —de nuevo, estos diagramas son para morfismos en la categoría monoidal M , y no en C— , lo que hace que el concepto de asociatividad de composición sea significativo en el caso general donde los objetos hom $C (a, b)$ son abstractos, y C en sí mismo no necesita siquiera tener ninguna noción de morfismo individual.

La noción de que una categoría ordinaria debe tener morfismos identidad es reemplazada por el segundo y tercer diagrama, que expresan la identidad en términos de unitores izquierdo y derecho :

Volviendo al caso en que M es la categoría de conjuntos con producto cartesiano, los morfismos $id a : I \to C (a, a)$ se convierten en funciones del conjunto unipuntual I y deben entonces, para cualquier objeto dado a , identificar un elemento particular de cada conjunto $C (a, a)$ , algo que podemos entonces pensar como el "morfismo identidad para a en C ". La conmutatividad de los dos últimos diagramas es entonces la afirmación de que las composiciones (tal como se definen por las funciones °) que involucran estos distinguidos "morfismos identidad en C " individuales se comportan exactamente según las reglas de identidad para categorías ordinarias.

Téngase en cuenta que aquí se hace referencia a varias nociones distintas de "identidad":

el objeto identidad monoidal $I$ de M , siendo una identidad para ⊗ sólo en el sentido monoide -teórico, e incluso entonces sólo hasta el isomorfismo canónico $(λ, ρ)$ .
el morfismo identidad $1 C (a, b) : C (a, b) \to C (a, b)$ que M tiene para cada uno de sus objetos en virtud de ser (al menos) una categoría ordinaria.
la identidad de categoría enriquecida $id a : I \to C (a, a)$ para cada objeto a en C , que es nuevamente un morfismo de M que, incluso en el caso en que se considera que C tiene sus propios morfismos individuales, no necesariamente identifica a uno específico.

Ejemplos de categorías enriquecidas

Las categorías ordinarias son categorías enriquecidas con ( Conjunto , ×, {•}), la categoría de conjuntos con producto cartesiano como operación monoidal, como se señaló anteriormente.
Las 2-Categorías son categorías enriquecidas sobre Cat , la categoría de las categorías pequeñas , con estructura monoidal dada por el producto cartesiano. En este caso las 2-celdas entre los morfismos a → b y la regla de composición vertical que las relaciona corresponden a los morfismos de la categoría ordinaria C ( a , b ) y a su propia regla de composición.
Las categorías localmente pequeñas son categorías enriquecidas con ( SmSet , × ), la categoría de conjuntos pequeños con producto cartesiano como operación monoidal. (Una categoría localmente pequeña es aquella cuyos hom-objetos son conjuntos pequeños).
Las categorías localmente finitas , por analogía, son categorías enriquecidas con ( FinSet , ×), la categoría de conjuntos finitos con producto cartesiano como operación monoidal.
Si C es una categoría monoidal cerrada entonces C está enriquecida en sí misma.
Los conjuntos preordenados son categorías enriquecidas sobre una cierta categoría monoidal, 2 , que consiste en dos objetos y una única flecha no identidad entre ellos que podemos escribir como FALSO → VERDADERO , conjunción como la operación monoide y VERDADERO como su identidad monoidal. Los hom-objetos 2 ( a , b ) simplemente niegan o afirman una relación binaria particular sobre el par dado de objetos ( a , b ); para tener una notación más familiar podemos escribir esta relación como $a \leq b$ . La existencia de las composiciones y la identidad requeridas para una categoría enriquecida sobre 2 se traducen inmediatamente a los siguientes axiomas respectivamente

b ≤ c y a ≤ b ⇒ a ≤ c (transitividad)

VERDADERO ⇒ a ≤ a (reflexividad)

que no son otros que los axiomas para que ≤ sea un preorden. Y dado que todos los diagramas en 2 conmutan, este es el único contenido de los axiomas de categorías enriquecidas para categorías enriquecidas sobre 2 .

Los espacios métricos generalizados de William Lawvere , también conocidos como espacios pseudocuasimétricos , son categorías enriquecidas sobre los números reales extendidos no negativos $R +\infty$ , donde a este último se le da una estructura de categoría ordinaria a través de la inversa de su ordenamiento habitual (es decir, existe un morfismo r → s si y solo si r ≥ s ) y una estructura monoidal a través de la adición (+) y cero (0). Los hom-objetos $R +\infty (a, b)$ son esencialmente distancias d( a , b ), y la existencia de composición e identidad se traducen en

d( b , c ) + d( a , b ) ≥ d( a , c ) (desigualdad triangular)

0 ≥ d( a , a )

Las categorías con morfismos cero son categorías enriquecidas con ( Conjunto* , ∧ ), la categoría de conjuntos puntiagudos con producto de ruptura como operación monoidal; el punto especial de un objeto hom Hom( A , B ) corresponde al morfismo cero de A a B .
La categoría Ab de los grupos abelianos y la categoría R-Mod de los módulos sobre un anillo conmutativo , y la categoría Vect de los espacios vectoriales sobre un cuerpo dado están enriquecidas sobre sí mismas, donde los morfismos heredan la estructura algebraica "puntual". De manera más general, las categorías preaditivas son categorías enriquecidas sobre ( Ab , ⊗) con el producto tensorial como operación monoidal (pensando en los grupos abelianos como Z -módulos).

Relación con funtores monoidales

Si hay un funtor monoidal de una categoría monoidal M a una categoría monoidal N , entonces cualquier categoría enriquecida sobre M puede reinterpretarse como una categoría enriquecida sobre N . Toda categoría monoidal M tiene un funtor monoidal M ( I , –) a la categoría de conjuntos, por lo que cualquier categoría enriquecida tiene una categoría ordinaria subyacente. En muchos ejemplos (como los anteriores) este funtor es faithful , por lo que una categoría enriquecida sobre M puede describirse como una categoría ordinaria con cierta estructura o propiedades adicionales.

Functores enriquecidos

Un funtor enriquecido es la generalización apropiada de la noción de funtor a categorías enriquecidas. Los funtores enriquecidos son entonces aplicaciones entre categorías enriquecidas que respetan la estructura enriquecida.

Si C y D son M -categorías (es decir, categorías enriquecidas sobre la categoría monoidal M ), un funtor M -enriquecido T : C → D es una función que asigna a cada objeto de C un objeto de D y para cada par de objetos a y b en C proporciona un morfismo en MT T _ab : C ( a , b ) → D ( T ( a ), T ( b )) entre los hom-objetos de C y D (que son objetos en M ), satisfaciendo versiones enriquecidas de los axiomas de un funtor, a saber, la preservación de la identidad y la composición.

Como los objetos hom no tienen por qué ser conjuntos de una categoría enriquecida, no se puede hablar de un morfismo particular. Ya no existe la noción de un morfismo identidad ni de una composición particular de dos morfismos. En cambio, los morfismos de la unidad a un objeto hom deben considerarse como la selección de una identidad, y los morfismos del producto monoidal deben considerarse como una composición. Los axiomas funtoriales habituales se sustituyen por los diagramas conmutativos correspondientes que implican estos morfismos.

En detalle, se tiene que el diagrama

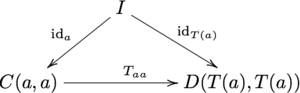
desplazamientos, lo que equivale a la ecuación

T_{aa}\circ \operatorname {id} _{a}=\operatorname {id} _{T(a)},

donde I es el objeto unitario de M. Esto es análogo a la regla F (id _a ) = id _{F ( a )} para funtores ordinarios. Además, se exige que el diagrama

conmuta, que es análoga a la regla F ( fg )= F ( f ) F ( g ) para funtores ordinarios.

Véase también

Referencias

Kelly, GM (2005) [1982]. Conceptos básicos de la teoría de categorías enriquecidas. Reimpresiones en Teoría y aplicaciones de categorías. Vol. 10.
Mac Lane, Saunders (septiembre de 1998). Categorías para el matemático en activo . Textos de posgrado en matemáticas . Vol. 5 (2.ª ed.). Springer. ISBN 0-387-98403-8.
Lawvere, FW (2002) [1973]. Espacios métricos, lógica generalizada y categorías cerradas. Reimpresiones en Teoría y aplicaciones de categorías. Vol. 1.
Categoría enriquecida en el n Lab