
La eclíptica o plano eclíptico es el plano orbital de la Tierra alrededor del Sol . [1] [2] [a] Desde la perspectiva de un observador en la Tierra, el movimiento del Sol alrededor de la esfera celeste a lo largo de un año traza una trayectoria a lo largo de la eclíptica contra el fondo de estrellas . [3] La eclíptica es un plano de referencia importante y es la base del sistema de coordenadas de la eclíptica .
La eclíptica es la trayectoria aparente del Sol a lo largo de un año . [4]
Como la Tierra tarda un año en orbitar alrededor del Sol, la posición aparente del Sol tarda un año en dar una vuelta completa a la eclíptica. Con un poco más de 365 días en un año, el Sol se mueve un poco menos de 1° hacia el este [5] cada día. Esta pequeña diferencia en la posición del Sol con respecto a las estrellas hace que cualquier punto particular en la superficie de la Tierra alcance al Sol (y se sitúe directamente al norte o al sur de él) unos cuatro minutos más tarde cada día de lo que lo haría si la Tierra no orbitara; por lo tanto, un día en la Tierra dura 24 horas en lugar del día sideral de aproximadamente 23 horas y 56 minutos . Nuevamente, esto es una simplificación, basada en una Tierra hipotética que orbita a una velocidad uniforme alrededor del Sol. La velocidad real con la que la Tierra orbita alrededor del Sol varía ligeramente durante el año, por lo que la velocidad con la que el Sol parece moverse a lo largo de la eclíptica también varía. Por ejemplo, el Sol está al norte del ecuador celeste durante unos 185 días de cada año, y al sur de él durante unos 180 días. [6] La variación de la velocidad orbital explica parte de la ecuación del tiempo . [7]
Debido al movimiento de la Tierra alrededor del centro de masas Tierra-Luna , la trayectoria aparente del Sol oscila ligeramente, con un período de aproximadamente un mes . Debido a otras perturbaciones de los otros planetas del Sistema Solar , el baricentro Tierra-Luna oscila ligeramente alrededor de una posición media de una manera compleja.
Debido a que el eje de rotación de la Tierra no es perpendicular a su plano orbital , el plano ecuatorial de la Tierra no es coplanar con el plano de la eclíptica, sino que está inclinado con respecto a él en un ángulo de aproximadamente 23,4°, que se conoce como la oblicuidad de la eclíptica . [8] Si el ecuador se proyecta hacia afuera a la esfera celeste , formando el ecuador celeste , cruza la eclíptica en dos puntos conocidos como equinoccios . El Sol, en su movimiento aparente a lo largo de la eclíptica, cruza el ecuador celeste en estos puntos, uno de sur a norte, el otro de norte a sur. [5] El cruce de sur a norte se conoce como equinoccio de marzo , también conocido como el primer punto de Aries y el nodo ascendente de la eclíptica en el ecuador celeste. [9] El cruce de norte a sur es el equinoccio de septiembre o nodo descendente .
La orientación del eje y el ecuador de la Tierra no son fijos en el espacio, sino que giran alrededor de los polos de la eclíptica con un período de unos 26.000 años, un proceso conocido como precesión lunisolar , ya que se debe principalmente al efecto gravitatorio de la Luna y el Sol sobre el abultamiento ecuatorial de la Tierra . Del mismo modo, la eclíptica en sí no es fija. Las perturbaciones gravitacionales de los otros cuerpos del Sistema Solar provocan un movimiento mucho menor del plano de la órbita de la Tierra, y por tanto de la eclíptica, conocido como precesión planetaria . La acción combinada de estos dos movimientos se llama precesión general , y cambia la posición de los equinoccios en unos 50 segundos de arco (unos 0,014°) por año. [10]
Una vez más, se trata de una simplificación. Los movimientos periódicos de la Luna y los movimientos periódicos aparentes del Sol (en realidad, de la Tierra en su órbita) causan oscilaciones periódicas de pequeña amplitud y corta duración del eje de la Tierra y, por lo tanto, del ecuador celeste, conocidas como nutación . [11] Esto añade un componente periódico a la posición de los equinoccios; las posiciones del ecuador celeste y del equinoccio (de marzo) con precesión y nutación completamente actualizadas se denominan ecuador y equinoccio verdaderos ; las posiciones sin nutación son el ecuador y equinoccio medios . [12]
La oblicuidad de la eclíptica es el término que utilizan los astrónomos para referirse a la inclinación del ecuador de la Tierra con respecto a la eclíptica, o del eje de rotación de la Tierra con respecto a una perpendicular a la eclíptica. Es de aproximadamente 23,4° y actualmente está disminuyendo 0,013 grados (47 segundos de arco) cada cien años debido a las perturbaciones planetarias. [13]
El valor angular de la oblicuidad se obtiene mediante la observación de los movimientos de la Tierra y otros planetas a lo largo de muchos años. Los astrónomos producen nuevas efemérides fundamentales a medida que mejora la precisión de la observación y aumenta la comprensión de la dinámica , y a partir de estas efemérides se derivan diversos valores astronómicos, incluida la oblicuidad.
Hasta 1983 la oblicuidad para cualquier fecha se calculaba a partir del trabajo de Newcomb , quien analizó las posiciones de los planetas hasta aproximadamente 1895:
ε = 23°27′08.26″ − 46.845″ T − 0.0059″ T 2 + 0.00181″ T 3
donde ε es la oblicuidad y T son los siglos tropicales desde B1900.0 hasta la fecha en cuestión. [15]
A partir de 1984, la serie DE de efemérides generadas por ordenador del Laboratorio de Propulsión a Chorro pasó a ser la efeméride fundamental del Almanaque Astronómico . La oblicuidad basada en DE200, que analizó las observaciones realizadas entre 1911 y 1979, se calculó:
ε = 23°26′21.45″ − 46.815″ T − 0.0006″ T 2 + 0.00181″ T 3
donde de aquí en adelante T son siglos julianos a partir de J2000.0 . [16]
Las efemérides fundamentales del JPL se han actualizado continuamente. El Almanaque Astronómico de 2010 especifica: [17]
ε = 23°26′21.406″ − 46.836769″ T − 0.0001831″ T 2 + 0.00200340″ T 3 − 0.576×10 −6 ″ T 4 − 4.34×10 −8 ″ T 5
Estas expresiones para la oblicuidad están pensadas para una alta precisión en un lapso de tiempo relativamente corto, quizás varios siglos. [18] J. Laskar calculó una expresión para ordenar T 10 con un valor de 0,04″ /1000 años durante 10 000 años. [14]
Todas estas expresiones son para la oblicuidad media , es decir, sin incluir la nutación del ecuador. La oblicuidad verdadera o instantánea incluye la nutación. [19]
La mayoría de los cuerpos principales del Sistema Solar orbitan alrededor del Sol en casi el mismo plano. Esto probablemente se deba a la forma en que el Sistema Solar se formó a partir de un disco protoplanetario . Probablemente la representación actual más cercana del disco se conoce como el plano invariable del Sistema Solar . La órbita de la Tierra, y por lo tanto, la eclíptica, está inclinada un poco más de 1° con respecto al plano invariable, la órbita de Júpiter está a un poco más de ½° de ella y los otros planetas principales están todos a unos 6°. Debido a esto, la mayoría de los cuerpos del Sistema Solar aparecen muy cerca de la eclíptica en el cielo.
El plano invariable se define por el momento angular de todo el Sistema Solar, esencialmente la suma vectorial de todos los momentos angulares orbitales y rotacionales de todos los cuerpos del sistema; más del 60% del total proviene de la órbita de Júpiter. [20] Esa suma requiere un conocimiento preciso de cada objeto del sistema, lo que la convierte en un valor algo incierto. Debido a la incertidumbre con respecto a la ubicación exacta del plano invariable, y debido a que la eclíptica está bien definida por el movimiento aparente del Sol, la eclíptica se utiliza como el plano de referencia del Sistema Solar tanto por precisión como por conveniencia. El único inconveniente de utilizar la eclíptica en lugar del plano invariable es que, en escalas de tiempo geológicas, se moverá contra puntos de referencia fijos en el fondo distante del cielo. [21] [22]

La eclíptica forma uno de los dos planos fundamentales que se utilizan como referencia para las posiciones en la esfera celeste, siendo el otro el ecuador celeste . Perpendiculares a la eclíptica están los polos eclípticos , siendo el polo norte de la eclíptica el polo al norte del ecuador. De los dos planos fundamentales, la eclíptica es más bien inmóvil con respecto a las estrellas de fondo, siendo su movimiento debido a la precesión planetaria aproximadamente 1/100 del del ecuador celeste. [23]
Las coordenadas esféricas , conocidas como longitud y latitud eclípticas o longitud y latitud celestes, se utilizan para especificar las posiciones de los cuerpos en la esfera celeste con respecto a la eclíptica. La longitud se mide positivamente hacia el este [5] de 0° a 360° a lo largo de la eclíptica desde el equinoccio de marzo, la misma dirección en la que parece moverse el Sol. La latitud se mide perpendicularmente a la eclíptica, a +90° hacia el norte o −90° hacia el sur hasta los polos de la eclíptica, siendo la eclíptica misma una latitud de 0°. Para una posición esférica completa, también es necesario un parámetro de distancia. Se utilizan diferentes unidades de distancia para diferentes objetos. Dentro del Sistema Solar, se utilizan unidades astronómicas , y para los objetos cercanos a la Tierra , se utilizan radios terrestres o kilómetros . Ocasionalmente también se utiliza un sistema de coordenadas rectangulares dextrógiros correspondiente ; el eje x se dirige hacia el equinoccio de marzo, el eje y 90° hacia el este y el eje z hacia el polo norte de la eclíptica; La unidad astronómica es la unidad de medida. Los símbolos de las coordenadas eclípticas están algo estandarizados; véase la tabla. [24]
Las coordenadas de la eclíptica son convenientes para especificar las posiciones de los objetos del Sistema Solar, ya que la mayoría de las órbitas de los planetas tienen pequeñas inclinaciones respecto de la eclíptica y, por lo tanto, siempre aparecen relativamente cerca de ella en el cielo. Debido a que la órbita de la Tierra, y por lo tanto la eclíptica, se mueve muy poco, es una referencia relativamente fija con respecto a las estrellas.
Debido al movimiento de precesión del equinoccio , las coordenadas eclípticas de los objetos en la esfera celeste cambian continuamente. Especificar una posición en coordenadas eclípticas requiere especificar un equinoccio particular, es decir, el equinoccio de una fecha particular, conocida como época ; las coordenadas se refieren a la dirección del equinoccio en esa fecha. Por ejemplo, el Almanaque Astronómico [27] enumera la posición heliocéntrica de Marte a las 0 h hora terrestre del 4 de enero de 2010 como: longitud 118°09′15.8″, latitud +1°43′16.7″, distancia heliocéntrica verdadera 1.6302454 UA, equinoccio medio y eclíptica de la fecha. Esto especifica el equinoccio medio del 4 de enero de 2010 a las 0 h TT como se indicó anteriormente, sin la adición de nutación.
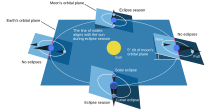
Como la órbita de la Luna está inclinada sólo unos 5,145° respecto de la eclíptica y el Sol está siempre muy cerca de ella, los eclipses siempre ocurren en ella o cerca de ella. Debido a la inclinación de la órbita de la Luna, los eclipses no ocurren en cada conjunción y oposición del Sol y la Luna, sino sólo cuando la Luna está cerca de un nodo ascendente o descendente al mismo tiempo que está en conjunción ( nueva ) u oposición ( llena ). La eclíptica recibe ese nombre porque los antiguos observaron que los eclipses sólo ocurren cuando la Luna la cruza. [28]
Los instantes exactos de los equinoccios y solsticios son los momentos en que la longitud eclíptica aparente (incluyendo los efectos de aberración y nutación ) del Sol es 0°, 90°, 180° y 270°. Debido a las perturbaciones de la órbita de la Tierra y a las anomalías del calendario , las fechas de estos eventos no son fijas. [29]

La eclíptica pasa actualmente por las siguientes constelaciones :
Las constelaciones de Cetus , Orión y Sextans no están en la eclíptica, pero están lo suficientemente cerca como para que la Luna y los planetas puedan aparecer ocasionalmente en ellas. [31]
La eclíptica forma el centro del zodíaco , un cinturón celeste de unos 20° de ancho en latitud a través del cual el Sol, la Luna y los planetas siempre parecen moverse. [32] Tradicionalmente, esta región se divide en 12 signos de 30° de longitud, cada uno de los cuales se aproxima al movimiento del Sol en un mes. [33] En la antigüedad, los signos correspondían aproximadamente a 12 de las constelaciones que se extienden a ambos lados de la eclíptica. [34] Estos signos a veces todavía se utilizan en la terminología moderna. El " Primer Punto de Aries " recibió su nombre cuando el Sol del equinoccio de marzo estaba en realidad en la constelación de Aries ; desde entonces se ha movido a Piscis debido a la precesión de los equinoccios . [35]
astrología.