diagrama de feynman

Representación pictórica del comportamiento de las partículas subatómicas.

Richard Feynman en 1984

En física teórica , un diagrama de Feynman es una representación pictórica de las expresiones matemáticas que describen el comportamiento y la interacción de partículas subatómicas . El esquema lleva el nombre del físico estadounidense Richard Feynman , quien introdujo los diagramas en 1948. La interacción de partículas subatómicas puede ser compleja y difícil de entender; Los diagramas de Feynman ofrecen una visualización sencilla de lo que de otro modo sería una fórmula arcana y abstracta. Según David Kaiser , "Desde mediados del siglo XX, los físicos teóricos han recurrido cada vez más a esta herramienta para ayudarles a realizar cálculos críticos. Los diagramas de Feynman han revolucionado casi todos los aspectos de la física teórica". ^[1] Si bien los diagramas se aplican principalmente a la teoría cuántica de campos , también se pueden utilizar en otras áreas de la física, como la teoría del estado sólido . Frank Wilczek escribió que los cálculos que le valieron el Premio Nobel de Física de 2004 "habrían sido literalmente impensables sin los diagramas de Feynman, al igual que los cálculos [de Wilczek] que establecieron una ruta para la producción y observación de la partícula de Higgs ". ^[2]

Feynman utilizó la interpretación de Ernst Stueckelberg del positrón como si fuera un electrón que retrocede en el tiempo. ^[3] Por lo tanto, las antipartículas se representan moviéndose hacia atrás a lo largo del eje del tiempo en los diagramas de Feynman.

El cálculo de amplitudes de probabilidad en la física teórica de partículas requiere el uso de integrales bastante grandes y complicadas sobre un gran número de variables . Los diagramas de Feynman pueden representar gráficamente estas integrales.

Un diagrama de Feynman es una representación gráfica de una contribución perturbativa a la amplitud de transición o función de correlación de una teoría de campo estadística o de mecánica cuántica. Dentro de la formulación canónica de la teoría cuántica de campos, un diagrama de Feynman representa un término en la expansión de Wick de la matriz S perturbativa . Alternativamente, la formulación integral de trayectoria de la teoría cuántica de campos representa la amplitud de transición como una suma ponderada de todas las historias posibles del sistema desde el estado inicial hasta el final, en términos de partículas o campos. La amplitud de transición se da entonces como el elemento matricial de la matriz S entre los estados inicial y final del sistema cuántico.

Motivación e historia.

En este diagrama, un kaon , formado por un antiquark extraño y elevado , se desintegra tanto débil como fuertemente en tres piones , con pasos intermedios que involucran un bosón W y un gluón , representados por la onda sinusoidal azul y la espiral verde, respectivamente.

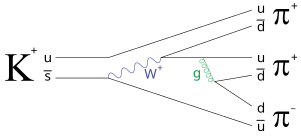
Al calcular las secciones transversales de dispersión en física de partículas , la interacción entre partículas se puede describir comenzando desde un campo libre que describe las partículas entrantes y salientes, e incluyendo una interacción hamiltoniana para describir cómo las partículas se desvían entre sí. La amplitud de la dispersión es la suma de cada posible historial de interacción sobre todos los posibles estados intermedios de partículas. El número de veces que actúa la interacción hamiltoniana es el orden de la expansión de la perturbación , y la teoría de la perturbación dependiente del tiempo para campos se conoce como serie de Dyson . Cuando los estados intermedios en tiempos intermedios son estados propios de energía (conjuntos de partículas con un momento definido), la serie se denomina teoría de perturbaciones antigua (o teoría de perturbaciones ordenada y dependiente del tiempo).

La serie de Dyson se puede reescribir alternativamente como una suma sobre los diagramas de Feynman, donde en cada vértice se conservan tanto la energía como el momento , pero donde la longitud del cuatro vector energía-momento no es necesariamente igual a la masa, es decir, las partículas intermedias. son los llamados off-shell . Los diagramas de Feynman son mucho más fáciles de seguir que los términos "anticuados", porque la forma antigua trata las contribuciones de partículas y antipartículas como separadas. Cada diagrama de Feynman es la suma exponencial de muchos términos antiguos, porque cada línea interna puede representar por separado una partícula o una antipartícula. En una teoría no relativista, no hay antipartículas y no hay duplicación, por lo que cada diagrama de Feynman incluye solo un término.

Feynman dio una receta para calcular la amplitud (las reglas de Feynman, más adelante) para cualquier diagrama dado a partir de una teoría de campos lagrangiana . Cada línea interna corresponde a un factor del propagador de la partícula virtual ; cada vértice donde se encuentran las líneas proporciona un factor derivado de un término de interacción en el lagrangiano, y las líneas entrantes y salientes llevan energía, impulso y espín .

Además de su valor como herramienta matemática, los diagramas de Feynman proporcionan una visión física profunda de la naturaleza de las interacciones entre partículas. Las partículas interactúan de todas las formas posibles; de hecho, a las partículas virtuales intermedias se les permite propagarse más rápido que la luz. La probabilidad de cada estado final se obtiene sumando todas esas posibilidades. Esto está estrechamente relacionado con la formulación integral funcional de la mecánica cuántica , también inventada por Feynman; ver formulación integral de trayectoria .

La aplicación ingenua de tales cálculos a menudo produce diagramas cuyas amplitudes son infinitas , porque las interacciones de partículas a corta distancia requieren un procedimiento de limitación cuidadoso, para incluir las autointeracciones de las partículas . La técnica de la renormalización , sugerida por Ernst Stueckelberg y Hans Bethe e implementada por Dyson , Feynman, Schwinger y Tomonaga , compensa este efecto y elimina los infinitos problemáticos. Después de la renormalización, los cálculos que utilizan diagramas de Feynman coinciden con los resultados experimentales con una precisión muy alta.

Los métodos del diagrama de Feynman y de la integral de ruta también se utilizan en mecánica estadística e incluso pueden aplicarse a la mecánica clásica . ^[4]

Nombres alternativos

Murray Gell-Mann siempre se refirió a los diagramas de Feynman como diagramas de Stueckelberg , en honor a un físico suizo, Ernst Stueckelberg , que ideó una notación similar muchos años antes. Stueckelberg estaba motivado por la necesidad de un formalismo manifiestamente covariante para la teoría cuántica de campos, pero no proporcionó una forma tan automatizada de manejar factores y bucles de simetría, aunque fue el primero en encontrar la interpretación física correcta en términos de avance y retroceso de partículas en el tiempo. caminos, todos sin la ruta integral. ^[5]

Históricamente, como instrumento de contabilidad de la teoría de la perturbación covariante, los gráficos se denominaron diagramas de Feynman-Dyson o gráficos de Dyson , ^[6] porque la integral de trayectoria no era familiar cuando se introdujeron y la derivación de Freeman Dyson de la perturbación antigua La teoría tomada de las expansiones perturbativas de la mecánica estadística era más fácil de seguir para los físicos formados en métodos anteriores. ^[a] Feynman tuvo que presionar mucho para obtener los diagramas, lo que confundió a los físicos establecidos entrenados en ecuaciones y gráficos. ^[7]

Representación de la realidad física.

En sus presentaciones de interacciones fundamentales , ^{[8] [9]} escritas desde la perspectiva de la física de partículas, Gerard 't Hooft y Martinus Veltman dieron buenos argumentos para tomar los diagramas de Feynman originales, no regularizados, como la representación más sucinta de nuestro conocimiento actual sobre la física de la dispersión cuántica de partículas fundamentales . Sus motivaciones son consistentes con las convicciones de James Daniel Bjorken y Sidney Drell : ^[10]

Los gráficos y las reglas de cálculo de Feynman resumen la teoría cuántica de campos de una forma que está en estrecho contacto con los números experimentales que uno quiere comprender. Aunque el enunciado de la teoría en términos de gráficos puede implicar la teoría de la perturbación , el uso de métodos gráficos en el problema de muchos cuerpos muestra que este formalismo es lo suficientemente flexible para abordar fenómenos de caracteres no perturbativos... Alguna modificación de las reglas de cálculo de Feynman bien podría sobrevivir a la elaborada estructura matemática de la teoría cuántica de campos canónica local...

En las teorías cuánticas de campos, los diagramas de Feynman se obtienen a partir de un lagrangiano mediante reglas de Feynman.

La regularización dimensional es un método para regularizar integrales en la evaluación de diagramas de Feynman; les asigna valores que son funciones meromórficas de un parámetro complejo auxiliar d , llamado dimensión. La regularización dimensional escribe una integral de Feynman como una integral dependiendo de la dimensión del espacio-tiempo d y los puntos del espacio-tiempo.

Interpretación del camino de las partículas

Un diagrama de Feynman es una representación de los procesos de la teoría cuántica de campos en términos de interacciones de partículas . Las partículas están representadas por las líneas del diagrama, que pueden ser onduladas o rectas, con flecha o sin ella, según el tipo de partícula. Un punto donde las líneas se conectan con otras líneas es un vértice , y aquí es donde las partículas se encuentran e interactúan: emitiendo o absorbiendo nuevas partículas, desviándose unas a otras o cambiando de tipo.

Hay tres tipos diferentes de líneas: las líneas internas conectan dos vértices, las líneas entrantes se extienden desde "el pasado" hasta un vértice y representan un estado inicial, y las líneas salientes se extienden desde un vértice hasta "el futuro" y representan el estado final (el Las dos últimas también se conocen como líneas externas ). Tradicionalmente, la parte inferior del diagrama es el pasado y la parte superior el futuro; otras veces, el pasado está a la izquierda y el futuro a la derecha. Al calcular funciones de correlación en lugar de amplitudes de dispersión , no hay pasado ni futuro y todas las líneas son internas. Luego, las partículas comienzan y terminan en pequeñas x, que representan las posiciones de los operadores cuya correlación se está calculando.

Los diagramas de Feynman son una representación pictórica de una contribución a la amplitud total de un proceso que puede ocurrir de varias maneras diferentes. Cuando un grupo de partículas entrantes se dispersan entre sí, se puede pensar en el proceso como uno en el que las partículas viajan por todos los caminos posibles, incluidos los que retroceden en el tiempo.

Los diagramas de Feynman a menudo se confunden con los diagramas de espacio-tiempo y las imágenes de la cámara de burbujas porque todos describen la dispersión de partículas. Los diagramas de Feynman son gráficos que representan la interacción de partículas en lugar de la posición física de la partícula durante un proceso de dispersión. A diferencia de una imagen de cámara de burbujas, sólo la suma de todos los diagramas de Feynman representa cualquier interacción de partículas determinada; las partículas no eligen un diagrama particular cada vez que interactúan. La ley de suma está de acuerdo con el principio de superposición : cada diagrama contribuye a la amplitud total del proceso.

Descripción

Características generales del proceso de dispersión A + B → C + D:
• líneas internas (rojas) para partículas y procesos intermedios, que tiene un factor de propagación ("prop"), líneas externas (naranja) para partículas entrantes/salientes hacia/desde vértices (negro) ,
• en cada vértice hay conservación de 4 momentos usando funciones delta, los 4 momentos que entran al vértice son positivos mientras que los que salen son negativos, los factores en cada vértice y línea interna se multiplican en la integral de amplitud,
• espacio Los ejes x y t del tiempo no siempre se muestran, las direcciones de las líneas externas corresponden al paso del tiempo.

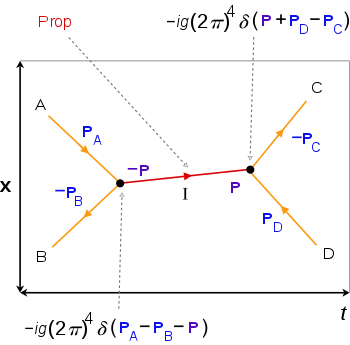
Un diagrama de Feynman representa una contribución perturbativa a la amplitud de una transición cuántica desde algún estado cuántico inicial a algún estado cuántico final.

Por ejemplo, en el proceso de aniquilación electrón-positrón el estado inicial es un electrón y un positrón, el estado final: dos fotones.

A menudo se supone que el estado inicial está a la izquierda del diagrama y el estado final a la derecha (aunque también se utilizan con bastante frecuencia otras convenciones).

Un diagrama de Feynman consta de puntos, llamados vértices, y líneas unidas a los vértices.

Las partículas en el estado inicial se representan mediante líneas que sobresalen en la dirección del estado inicial (p. ej., hacia la izquierda), las partículas en el estado final se representan mediante líneas que sobresalen en la dirección del estado final (p. ej., hacia la izquierda). la derecha).

En QED existen dos tipos de partículas: partículas de materia como electrones o positrones (llamadas fermiones ) y partículas de intercambio (llamadas bosones de calibre ). Se representan en diagramas de Feynman de la siguiente manera:

1. El electrón en el estado inicial está representado por una línea continua, con una flecha que indica el giro de la partícula, por ejemplo, apuntando hacia el vértice (→•).
2. El electrón en el estado final está representado por una línea, con una flecha que indica el giro de la partícula, por ejemplo, apuntando en dirección opuesta al vértice: (•→).
3. El positrón en el estado inicial está representado por una línea continua, con una flecha que indica el giro de la partícula, por ejemplo, apuntando en dirección opuesta al vértice: (←•).
4. El positrón en el estado final está representado por una línea, con una flecha que indica el giro de la partícula, por ejemplo apuntando hacia el vértice: (•←).
5. El fotón virtual en el estado inicial y final está representado por una línea ondulada ( ~• y •~ ).

En QED, un vértice siempre tiene tres líneas adjuntas: una línea bosónica, una línea fermiónica con una flecha hacia el vértice y una línea fermiónica con una flecha alejada del vértice.

Los vértices podrían estar conectados por un propagador bosónico o fermiónico . Un propagador bosónico está representado por una línea ondulada que conecta dos vértices (•~•). Un propagador fermiónico está representado por una línea continua (con una flecha en una u otra dirección) que conecta dos vértices, (•←•).

El número de vértices da el orden del término en la expansión de la serie de perturbaciones de la amplitud de transición.

Ejemplo de aniquilación electrón-positrón

Diagrama de Feynman de aniquilación electrón/positrón

La interacción de aniquilación electrón-positrón :

mi ⁺ + mi ⁻ → 2γ

tiene una contribución del diagrama de Feynman de segundo orden que se muestra al lado:

En el estado inicial (en la parte inferior; tiempo temprano) hay un electrón (e ⁻ ) y un positrón (e ⁺ ) y en el estado final (en la parte superior; tiempo tardío) hay dos fotones (γ).

Formulación de cuantificación canónica

La amplitud de probabilidad para una transición de un sistema cuántico (entre estados asintóticamente libres) del estado inicial |i⟩ al estado final | f ⟩ está dada por el elemento de la matriz

${\displaystyle S_{\rm {fi}}=\langle \mathrm {f} |S|\mathrm {i} \rangle \;,}$

donde S es la matriz S. En términos del operador de evolución temporal U , es simplemente

${\displaystyle S=\lim _{t_{2}\rightarrow +\infty }\lim _{t_{1}\rightarrow -\infty }U(t_{2},t_{1})\;.}$

En la imagen de interacción , esto se expande a

${\displaystyle S={\mathcal {T}}e^{-i\int _{-\infty }^{+\infty }d\tau H_{V}(\tau )}.}$

donde H _V es la interacción hamiltoniana y T significa el producto de operadores ordenado en el tiempo . La fórmula de Dyson expande la matriz exponencial ordenada en el tiempo en una serie de perturbaciones en las potencias de la interacción densidad hamiltoniana,

${\displaystyle S=\sum _{n=0}^{\infty }{\frac {(-i)^{n}}{n!}}\left(\prod _{j=1}^{n}\int d^{4}x_{j}\right){\mathcal {T}}\left\{\prod _{j=1}^{n}{\mathcal {H}}_{V}\left(x_{j}\right)\right\}\equiv \sum _{n=0}^{\infty }S^{(n)}\;.}$

De manera equivalente, con la interacción Lagrangiana L _V , es

${\displaystyle S=\sum _{n=0}^{\infty }{\frac {i^{n}}{n!}}\left(\prod _{j=1}^{n}\int d^{4}x_{j}\right){\mathcal {T}}\left\{\prod _{j=1}^{n}{\mathcal {L}}_{V}\left(x_{j}\right)\right\}\equiv \sum _{n=0}^{\infty }S^{(n)}\;.}$

Un diagrama de Feynman es una representación gráfica de un único sumando en la expansión de Wick del producto ordenado en el tiempo en el término de enésimo orden S ( ^{n ) de} la serie de Dyson de la matriz S.

${\displaystyle {\mathcal {T}}\prod _{j=1}^{n}{\mathcal {L}}_{V}\left(x_{j}\right)=\sum _{\text{A}}(\pm ){\mathcal {N}}\prod _{j=1}^{n}{\mathcal {L}}_{V}\left(x_{j}\right)\;,}$

donde N significa el producto ordenado normal de los operadores y (±) se encarga del posible cambio de signo al conmutar los operadores fermiónicos para reunirlos para una contracción (un propagador ) y A representa todas las contracciones posibles.

reglas de feynman

Los diagramas se dibujan según las reglas de Feynman, que dependen de la interacción lagrangiana. Para la interacción QED Lagrangiana

${\displaystyle L_{v}=-g{\bar {\psi }}\gamma ^{\mu }\psi A_{\mu }}$

Al describir la interacción de un campo fermiónico ψ con un campo calibre bosónico A _μ , las reglas de Feynman se pueden formular en el espacio de coordenadas de la siguiente manera:

1. Cada coordenada de integración x _j está representada por un punto (a veces llamado vértice);
2. Un propagador bosónico está representado por una línea ondulante que conecta dos puntos;
3. Un propagador fermiónico está representado por una línea continua que conecta dos puntos;
4. Un campo bosónico está representado por una línea ondulada unida al punto x _i ; ${\displaystyle A_{\mu }(x_{i})}$
5. Un campo fermiónico ψ ( x _i ) está representado por una línea continua unida al punto x _i con una flecha hacia el punto;
6. Un campo antifermiónico ψ ( x _i ) está representado por una línea continua unida al punto x _i con una flecha alejada del punto;

Ejemplo: procesos de segundo orden en QED

El término de perturbación de segundo orden en la matriz S es

${\displaystyle S^{(2)}={\frac {(ie)^{2}}{2!}}\int d^{4}x\,d^{4}x'\,T{\bar {\psi }}(x)\,\gamma ^{\mu }\,\psi (x)\,A_{\mu }(x)\,{\bar {\psi }}(x')\,\gamma ^{\nu }\,\psi (x')\,A_{\nu }(x').\;}$

Dispersión de fermiones

La expansión del integrando de Wick da (entre otros) el siguiente término

${\displaystyle N{\bar {\psi }}(x)\gamma ^{\mu }\psi (x){\bar {\psi }}(x')\gamma ^{\nu }\psi (x'){\underline {A_{\mu }(x)A_{\nu }(x')}}\;,}$

dónde

${\displaystyle {\underline {A_{\mu }(x)A_{\nu }(x')}}=\int {\frac {d^{4}k}{(2\pi )^{4}}}{\frac {-ig_{\mu \nu }}{k^{2}+i0}}e^{-ik(x-x')}}$

es la contracción electromagnética (propagador) en el calibre de Feynman. Este término está representado por el diagrama de Feynman a la derecha. Este diagrama aporta contribuciones a los siguientes procesos:

1. e ⁻ e ⁻ dispersión (estado inicial a la derecha, estado final a la izquierda del diagrama);
2. e ⁺ e ⁺ dispersión (estado inicial a la izquierda, estado final a la derecha del diagrama);
3. e ^- e ⁺ dispersión (estado inicial en la parte inferior/superior, estado final en la parte superior/inferior del diagrama).

Dispersión de Compton y aniquilación/generación de pares e ⁻ e ⁺

Otro término interesante en la expansión es

${\displaystyle N{\bar {\psi }}(x)\,\gamma ^{\mu }\,{\underline {\psi (x)\,{\bar {\psi }}(x')}}\,\gamma ^{\nu }\,\psi (x')\,A_{\mu }(x)\,A_{\nu }(x')\;,}$

dónde

${\displaystyle {\underline {\psi (x){\bar {\psi }}(x')}}=\int {\frac {d^{4}p}{(2\pi )^{4}}}{\frac {i}{\gamma p-m+i0}}e^{-ip(x-x')}}$

es la contracción fermiónica (propagadora).

Formulación integral de camino

En una integral de trayectoria , el campo lagrangiano, integrado sobre todas las historias de campo posibles, define la amplitud de probabilidad de pasar de una configuración de campo a otra. Para que tenga sentido, la teoría de campo debe tener un estado fundamental bien definido y la integral debe realizarse un poco rotada en tiempo imaginario, es decir, una rotación de Wick . El formalismo integral de ruta es completamente equivalente al formalismo de operador canónico anterior.

Campo escalar lagrangiano

Un ejemplo sencillo es el campo escalar relativista libre en d dimensiones, cuya integral de acción es:

${\displaystyle S=\int {\tfrac {1}{2}}\partial _{\mu }\phi \partial ^{\mu }\phi \,d^{d}x\,.}$

La amplitud de probabilidad de un proceso es:

${\displaystyle \int _{A}^{B}e^{iS}\,D\phi \,,}$

donde A y B son hipersuperficies espaciales que definen las condiciones de contorno. La colección de todos los φ ( A ) en la hipersuperficie inicial da el valor inicial del campo, análogo a la posición inicial de una partícula puntual, y los valores del campo φ ( B ) en cada punto de la hipersuperficie final definen el campo final. valor, que se permite variar, dando una amplitud diferente para terminar en valores diferentes. Esta es la amplitud de transición de campo a campo.

La integral de ruta da el valor esperado de los operadores entre el estado inicial y final:

${\displaystyle \int _{A}^{B}e^{iS}\phi (x_{1})\cdots \phi (x_{n})\,D\phi =\left\langle A\left|\phi (x_{1})\cdots \phi (x_{n})\right|B\right\rangle \,,}$

y en el límite en el que A y B retroceden hacia el pasado infinito y el futuro infinito, la única contribución que importa es la del estado fundamental (esto sólo es rigurosamente cierto si la integral de trayectoria se define ligeramente rotada en el tiempo imaginario). La integral de ruta puede considerarse análoga a una distribución de probabilidad, y es conveniente definirla de modo que multiplicar por una constante no cambie nada:

${\displaystyle {\frac {\displaystyle \int e^{iS}\phi (x_{1})\cdots \phi (x_{n})\,D\phi }{\displaystyle \int e^{iS}\,D\phi }}=\left\langle 0\left|\phi (x_{1})\cdots \phi (x_{n})\right|0\right\rangle \,.}$

El factor de normalización en la parte inferior se llama función de partición del campo y coincide con la función de partición mecánica estadística a temperatura cero cuando se gira en tiempo imaginario.

Las amplitudes desde el inicio hasta el final están mal definidas si se piensa en el límite del continuo desde el principio, porque las fluctuaciones en el campo pueden volverse ilimitadas. Por lo tanto, se puede pensar en la integral de ruta como en una red cuadrada discreta, con un espaciamiento de red a y el límite a → 0 debe tomarse con cuidado ^{[ se necesita aclaración ]} . Si los resultados finales no dependen de la forma de la red o del valor de a , entonces existe el límite continuo.

en una celosía

En una red, (i), el campo se puede expandir en modos de Fourier :

${\displaystyle \phi (x)=\int {\frac {dk}{(2\pi )^{d}}}\phi (k)e^{ik\cdot x}=\int _{k}\phi (k)e^{ikx}\,.}$

Aquí el dominio de integración está sobre k restringido a un cubo de longitud de lado2π/a, de modo que no se permiten valores grandes de k . Es importante tener en cuenta que la k -medida contiene los factores de 2 π de las transformadas de Fourier , esta es la mejor convención estándar para k -integrales en QFT. La red significa que no se permite que las fluctuaciones en general k contribuyan de inmediato, solo comienzan a contribuir en el límite a → 0 . A veces, en lugar de una red, los modos de campo simplemente se cortan en valores altos de k .

También es conveniente de vez en cuando considerar que el volumen del espacio-tiempo es finito, de modo que los k modos también sean una red. Esto no es estrictamente tan necesario como el límite de la red espacial, porque las interacciones en k no están localizadas, pero es conveniente para realizar un seguimiento de los factores delante de las k -integrales y las funciones delta que conservan el momento que surgirán.

En una red, (ii), la acción debe discretizarse:

${\displaystyle S=\sum _{\langle x,y\rangle }{\tfrac {1}{2}}{\big (}\phi (x)-\phi (y){\big )}^{2}\,,}$

donde ⟨ x , y ⟩ es un par de vecinos de red más cercanos x e y . Se debe considerar que la discretización define lo que significa la derivada ∂ _μ φ .

En términos de los modos reticulares de Fourier, la acción se puede escribir:

${\displaystyle S=\int _{k}{\Big (}{\big (}1-\cos(k_{1}){\big )}+{\big (}1-\cos(k_{2}){\big )}+\cdots +{\big (}1-\cos(k_{d}){\big )}{\Big )}\phi _{k}^{*}\phi ^{k}\,.}$

Para k cercano a cero esto es:

${\displaystyle S=\int _{k}{\tfrac {1}{2}}k^{2}\left|\phi (k)\right|^{2}\,.}$

Ahora tenemos la transformada continua de Fourier de la acción original. En volumen finito, la cantidad d ^d k no es infinitesimal, sino que se convierte en el volumen de una caja formada por modos de Fourier vecinos, o (2π/V)^d
 .

El campo φ tiene valor real, por lo que la transformada de Fourier obedece:

${\displaystyle \phi (k)^{*}=\phi (-k)\,.}$

En términos de partes real e imaginaria, la parte real de φ ( k ) es una función par de k , mientras que la parte imaginaria es impar. La transformada de Fourier evita la doble contabilización, por lo que se puede escribir:

${\displaystyle S=\int _{k}{\tfrac {1}{2}}k^{2}\phi (k)\phi (-k)}$

sobre un dominio de integración que integra cada par ( k , − k ) exactamente una vez.

Para un campo escalar complejo con acción

${\displaystyle S=\int {\tfrac {1}{2}}\partial _{\mu }\phi ^{*}\partial ^{\mu }\phi \,d^{d}x}$

la transformada de Fourier no tiene restricciones:

${\displaystyle S=\int _{k}{\tfrac {1}{2}}k^{2}\left|\phi (k)\right|^{2}}$

y la integral es sobre todo k .

Integrar sobre todos los valores diferentes de φ ( x ) es equivalente a integrar sobre todos los modos de Fourier, porque tomar una transformada de Fourier es una transformación lineal unitaria de coordenadas de campo. Cuando cambias las coordenadas en una integral multidimensional mediante una transformación lineal, el valor de la nueva integral viene dado por el determinante de la matriz de transformación. Si

${\displaystyle y_{i}=A_{ij}x_{j}\,,}$

entonces

${\displaystyle \det(A)\int dx_{1}\,dx_{2}\cdots \,dx_{n}=\int dy_{1}\,dy_{2}\cdots \,dy_{n}\,.}$

Si A es una rotación, entonces

${\displaystyle A^{\mathrm {T} }A=I}$

de modo que det A = ±1 , y el signo depende de si la rotación incluye reflexión o no.

La matriz que cambia las coordenadas de φ ( x ) a φ ( k ) se puede leer a partir de la definición de una transformada de Fourier.

${\displaystyle A_{kx}=e^{ikx}\,}$

y el teorema de inversión de Fourier te dice lo inverso:

${\displaystyle A_{kx}^{-1}=e^{-ikx}\,}$

que es el complejo conjugado-transpuesto, hasta factores de 2 π . En una red de volumen finito, el determinante es distinto de cero e independiente de los valores del campo.

${\displaystyle \det A=1\,}$

y la integral de trayectoria es un factor separado en cada valor de k .

${\displaystyle \int \exp \left({\frac {i}{2}}\sum _{k}k^{2}\phi ^{*}(k)\phi (k)\right)\,D\phi =\prod _{k}\int _{\phi _{k}}e^{{\frac {i}{2}}k^{2}\left|\phi _{k}\right|^{2}\,d^{d}k}\,}$

El factor d ^d k es el volumen infinitesimal de una celda discreta en el espacio k , en una caja de celosía cuadrada

${\displaystyle d^{d}k=\left({\frac {1}{L}}\right)^{d}\,,}$

donde L es la longitud del lado de la caja. Cada factor separado es un gaussiano oscilatorio, y el ancho del gaussiano diverge a medida que el volumen llega al infinito.

En tiempo imaginario, la acción euclidiana se vuelve positiva definida y puede interpretarse como una distribución de probabilidad. La probabilidad de que un campo tenga valores φ _k es

${\displaystyle e^{\int _{k}-{\tfrac {1}{2}}k^{2}\phi _{k}^{*}\phi _{k}}=\prod _{k}e^{-k^{2}\left|\phi _{k}\right|^{2}\,d^{d}k}\,.}$

El valor esperado del campo es el valor esperado estadístico del campo cuando se elige según la distribución de probabilidad:

${\displaystyle \left\langle \phi (x_{1})\cdots \phi (x_{n})\right\rangle ={\frac {\displaystyle \int e^{-S}\phi (x_{1})\cdots \phi (x_{n})\,D\phi }{\displaystyle \int e^{-S}\,D\phi }}}$

Dado que la probabilidad de φ _k es un producto, el valor de φ _k en cada valor separado de k tiene una distribución gaussiana independiente. La varianza del gaussiano es1/k ² d ^d k, que es formalmente infinito, pero eso simplemente significa que las fluctuaciones son ilimitadas en un volumen infinito. En cualquier volumen finito, la integral se reemplaza por una suma discreta y la varianza de la integral esV/k ².

Monte Carlo

La integral de ruta define un algoritmo probabilístico para generar una configuración de campo escalar euclidiano. Elija aleatoriamente las partes real e imaginaria de cada modo de Fourier en el número de onda k para que sea una variable aleatoria gaussiana con varianza1/k ². Esto genera una configuración φ _C ( k ) aleatoria, y la transformada de Fourier da φ _C ( x ) . Para campos escalares reales, el algoritmo debe generar solo uno de cada par φ ( k ), φ (− k ) y hacer que el segundo sea el conjugado complejo del primero.

Para encontrar cualquier función de correlación, genere un campo una y otra vez mediante este procedimiento y encuentre el promedio estadístico:

${\displaystyle \left\langle \phi (x_{1})\cdots \phi (x_{n})\right\rangle =\lim _{|C|\rightarrow \infty }{\frac {\displaystyle \sum _{C}\phi _{C}(x_{1})\cdots \phi _{C}(x_{n})}{|C|}}}$

donde | C | es el número de configuraciones y la suma es el producto de los valores de campo en cada configuración. La función de correlación euclidiana es igual que la función de correlación en estadística o mecánica estadística. Las funciones de correlación de la mecánica cuántica son una continuación analítica de las funciones de correlación euclidianas.

Para campos libres con acción cuadrática, la distribución de probabilidad es gaussiana de alta dimensión y el promedio estadístico viene dado por una fórmula explícita. Pero el método de Monte Carlo también funciona bien para teorías de campos de interacción bosónica donde no existe una forma cerrada para las funciones de correlación.

propagador escalar

Cada modo tiene una distribución gaussiana independiente. La expectativa de los modos de campo es fácil de calcular:

${\displaystyle \left\langle \phi _{k}\phi _{k'}\right\rangle =0\,}$

para k ≠ k ′ , desde entonces las dos variables aleatorias gaussianas son independientes y ambas tienen media cero.

${\displaystyle \left\langle \phi _{k}\phi _{k}\right\rangle ={\frac {V}{k^{2}}}}$

en volumen finito V , cuando los dos k -valores coinciden, ya que esta es la varianza del Gaussiano. En el límite de volumen infinito,

${\displaystyle \left\langle \phi (k)\phi (k')\right\rangle =\delta (k-k'){\frac {1}{k^{2}}}}$

Estrictamente hablando, esto es una aproximación: el propagador de red es:

${\displaystyle \left\langle \phi (k)\phi (k')\right\rangle =\delta (k-k'){\frac {1}{2{\big (}d-\cos(k_{1})+\cos(k_{2})\cdots +\cos(k_{d}){\big )}}}}$

Pero cerca de k = 0 , para fluctuaciones de campo largas en comparación con el espaciamiento de la red, las dos formas coinciden.

Es importante enfatizar que las funciones delta contienen factores de 2 π , de modo que cancelan los factores de 2 π en la medida para k integrales.

${\displaystyle \delta (k)=(2\pi )^{d}\delta _{D}(k_{1})\delta _{D}(k_{2})\cdots \delta _{D}(k_{d})\,}$

donde δ _D ( k ) es la función delta de Dirac unidimensional ordinaria. Esta convención para funciones delta no es universal: algunos autores mantienen explícitos los factores de 2 π en las funciones delta (y en la k -integración).

Ecuación de movimiento

La forma del propagador se puede encontrar más fácilmente usando la ecuación de movimiento del campo. Del lagrangiano, la ecuación de movimiento es:

${\displaystyle \partial _{\mu }\partial ^{\mu }\phi =0\,}$

y en un valor esperado, esto dice:

${\displaystyle \partial _{\mu }\partial ^{\mu }\left\langle \phi (x)\phi (y)\right\rangle =0}$

Donde las derivadas actúan sobre x y la identidad es verdadera en todas partes excepto cuando xey coinciden, y el orden de los operadores es importante . La forma de la singularidad puede entenderse a partir de las relaciones de conmutación canónicas como una función delta. Definir el propagador (euclidiano) de Feynman Δ como la transformada de Fourier de la función de dos puntos ordenada en el tiempo (la que proviene de la integral de ruta):

${\displaystyle \partial ^{2}\Delta (x)=i\delta (x)\,}$

De modo que:

${\displaystyle \Delta (k)={\frac {i}{k^{2}}}}$

Si las ecuaciones de movimiento son lineales, el propagador siempre será el recíproco de la matriz de forma cuadrática que define el lagrangiano libre, ya que ésta da las ecuaciones de movimiento. Esto también es fácil de ver directamente desde la integral de ruta. El factor de i desaparece en la teoría euclidiana.

Teorema de mecha

Debido a que cada modo de campo es un gaussiano independiente, los valores esperados para el producto de muchos modos de campo obedecen al teorema de Wick :

${\displaystyle \left\langle \phi (k_{1})\phi (k_{2})\cdots \phi (k_{n})\right\rangle }$

es cero a menos que los modos de campo coincidan en pares. Esto significa que es cero para un número impar de φ , y para un número par de φ , es igual a una contribución de cada par por separado, con una función delta.

${\displaystyle \left\langle \phi (k_{1})\cdots \phi (k_{2n})\right\rangle =\sum \prod _{i,j}{\frac {\delta \left(k_{i}-k_{j}\right)}{k_{i}^{2}}}}$

donde la suma está sobre cada partición de los modos de campo en pares, y el producto está sobre los pares. Por ejemplo,

${\displaystyle \left\langle \phi (k_{1})\phi (k_{2})\phi (k_{3})\phi (k_{4})\right\rangle ={\frac {\delta (k_{1}-k_{2})}{k_{1}^{2}}}{\frac {\delta (k_{3}-k_{4})}{k_{3}^{2}}}+{\frac {\delta (k_{1}-k_{3})}{k_{3}^{2}}}{\frac {\delta (k_{2}-k_{4})}{k_{2}^{2}}}+{\frac {\delta (k_{1}-k_{4})}{k_{1}^{2}}}{\frac {\delta (k_{2}-k_{3})}{k_{2}^{2}}}}$

Una interpretación del teorema de Wick es que cada inserción de campo puede considerarse como una línea colgante, y el valor esperado se calcula uniendo las líneas en pares, poniendo un factor de función delta que garantiza que el impulso de cada socio en el par sea igual y dividiendo por el propagador.

Momentos gaussianos superiores: cumplimiento del teorema de Wick

Queda un punto sutil antes de demostrar el teorema de Wick: ¿qué pasa si más de dos de los s tienen el mismo impulso? Si es un número impar, la integral es cero; los valores negativos se cancelan con los valores positivos. Pero si el número es par, la integral es positiva. La demostración anterior suponía que las s sólo coincidirían en pares. ${\displaystyle \phi }$ ${\displaystyle \phi }$

Pero el teorema es correcto incluso cuando muchos de ellos son iguales, y ésta es una propiedad notable de la integración gaussiana: ${\displaystyle \phi }$

${\displaystyle I=\int e^{-ax^{2}/2}dx={\sqrt {\frac {2\pi }{a}}}}$

${\displaystyle {\frac {\partial ^{n}}{\partial a^{n}}}I=\int {\frac {x^{2n}}{2^{n}}}e^{-ax^{2}/2}dx={\frac {1\cdot 3\cdot 5\ldots \cdot (2n-1)}{2\cdot 2\cdot 2\ldots \;\;\;\;\;\cdot 2\;\;\;\;\;\;}}{\sqrt {2\pi }}\,a^{-{\frac {2n+1}{2}}}}$

Dividiendo por yo ,

${\displaystyle \left\langle x^{2n}\right\rangle ={\frac {\displaystyle \int x^{2n}e^{-ax^{2}/2}}{\displaystyle \int e^{-ax^{2}/2}}}=1\cdot 3\cdot 5\ldots \cdot (2n-1){\frac {1}{a^{n}}}}$

${\displaystyle \left\langle x^{2}\right\rangle ={\frac {1}{a}}}$

Si el teorema de Wick fuera correcto, los momentos superiores estarían dados por todos los pares posibles de una lista de 2 n x diferentes :

${\displaystyle \left\langle x_{1}x_{2}x_{3}\cdots x_{2n}\right\rangle }$

donde las x son todas la misma variable, el índice es solo para realizar un seguimiento de la cantidad de formas de emparejarlas. La primera x se puede emparejar con 2 n − 1 más, dejando 2 n − 2 . La siguiente x no apareada se puede emparejar con 2 n − 3 x diferentes dejando 2 n − 4 , y así sucesivamente. Esto significa que el teorema de Wick, sin corregir, dice que el valor esperado de x ^{2 n} debería ser:

${\displaystyle \left\langle x^{2n}\right\rangle =(2n-1)\cdot (2n-3)\ldots \cdot 5\cdot 3\cdot 1\left\langle x^{2}\right\rangle ^{n}}$

y esta es de hecho la respuesta correcta. Por tanto, el teorema de Wick se cumple sin importar cuántos momentos de las variables internas coincidan.

Interacción

Las interacciones están representadas por contribuciones de orden superior, ya que las contribuciones cuadráticas son siempre gaussianas. La interacción más simple es la autointeracción cuártica, con una acción:

${\displaystyle S=\int \partial ^{\mu }\phi \partial _{\mu }\phi +{\frac {\lambda }{4!}}\phi ^{4}.}$

¡La razón del factor combinatorio 4! quedará claro pronto. Escribir la acción en términos de los modos de Fourier reticulares (o continuos):

${\displaystyle S=\int _{k}k^{2}\left|\phi (k)\right|^{2}+{\frac {\lambda }{4!}}\int _{k_{1}k_{2}k_{3}k_{4}}\phi (k_{1})\phi (k_{2})\phi (k_{3})\phi (k_{4})\delta (k_{1}+k_{2}+k_{3}+k_{4})=S_{F}+X.}$

Donde S _F es la acción libre, cuyas funciones de correlación vienen dadas por el teorema de Wick. La exponencial de S en la integral de trayectoria se puede expandir en potencias de λ , dando una serie de correcciones a la acción libre.

${\displaystyle e^{-S}=e^{-S_{F}}\left(1+X+{\frac {1}{2!}}XX+{\frac {1}{3!}}XXX+\cdots \right)}$

La integral de trayectoria para la acción interactuante es entonces una serie de potencias de correcciones a la acción libre. El término representado por X debe considerarse como cuatro medias líneas, una para cada factor de φ ( k ) . Las medias líneas se encuentran en un vértice, lo que aporta una función delta que garantiza que la suma de los momentos sea igual.

Para calcular una función de correlación en la teoría de la interacción, ahora existe una contribución de los términos X. Por ejemplo, la integral de ruta para el correlacionador de cuatro campos:

${\displaystyle \left\langle \phi (k_{1})\phi (k_{2})\phi (k_{3})\phi (k_{4})\right\rangle ={\frac {\displaystyle \int e^{-S}\phi (k_{1})\phi (k_{2})\phi (k_{3})\phi (k_{4})D\phi }{Z}}}$

que en el campo libre sólo era distinto de cero cuando los momentos k eran iguales en pares, ahora es distinto de cero para todos los valores de k . Los momentos de las inserciones φ ( k _i ) ahora pueden coincidir con los momentos de las X s en la expansión. Las inserciones también deben considerarse como medias líneas, cuatro en este caso, que llevan un momento k , pero que no está integrado.

La contribución de orden más bajo proviene del primer término no trivial e ^{− S _F} X en la expansión de Taylor de la acción. El teorema de Wick requiere que los momentos en las semilíneas X , los factores φ ( k ) en X , coincidan con los momentos de las semilíneas externas en pares. La nueva contribución es igual a:

${\displaystyle \lambda {\frac {1}{k_{1}^{2}}}{\frac {1}{k_{2}^{2}}}{\frac {1}{k_{3}^{2}}}{\frac {1}{k_{4}^{2}}}\,.}$

¡Los 4! ¡ Dentro de X se cancela porque hay exactamente 4! formas de hacer coincidir las medias líneas en X con las medias líneas externas. Cada una de estas diferentes formas de unir las medias líneas en pares contribuye exactamente una vez, independientemente de los valores de k _1,2,3,4 , según el teorema de Wick.

diagramas de feynman

La expansión de la acción en potencias de X da una serie de términos con un número progresivamente mayor de X s. La contribución del término con exactamente n X s se llama de orden n .

Los términos de enésimo orden tienen:

1. 4 n medias líneas internas, que son los factores de φ ( k ) de las X s. Todos estos terminan en un vértice y están integrados en todos los k posibles .
2. medias líneas externas, que provienen de las inserciones φ ( k ) en la integral.

Según el teorema de Wick, cada par de medias líneas debe emparejarse para formar una línea , y esta línea da un factor de

${\displaystyle {\frac {\delta (k_{1}+k_{2})}{k_{1}^{2}}}}$

lo que multiplica la contribución. Esto significa que las dos medias líneas que forman una línea se ven obligadas a tener un impulso igual y opuesto. La línea en sí debe estar etiquetada con una flecha, dibujada paralela a la línea y etiquetada por el impulso en la línea k . La media línea en el extremo final de la flecha lleva el impulso k , mientras que la media línea en el extremo superior lleva el impulso − k . Si una de las dos medias líneas es externa, esto mata la integral sobre la k interna , ya que obliga a la k interna a ser igual a la k externa . Si ambos son internos, la integral sobre k permanece.

Los diagramas que se forman uniendo las medias líneas en las X con las medias líneas externas, que representan inserciones, son los diagramas de Feynman de esta teoría. Cada línea lleva un factor de1/k ², el propagador, y va de vértice a vértice o termina en una inserción. Si es interno, se integra encima. En cada vértice, el total k entrante es igual al total k saliente .

¡La cantidad de formas de hacer un diagrama uniendo medias líneas en líneas anula casi por completo los factores factoriales provenientes de la serie de Taylor de la exponencial y la 4! en cada vértice.

Orden de bucle

Un diagrama de bosque es aquel en el que todas las líneas internas tienen un impulso que está completamente determinado por las líneas externas y la condición de que el impulso entrante y saliente sean iguales en cada vértice. El aporte de estos diagramas es producto de propagadores, sin integración alguna. Un diagrama de árbol es un diagrama de bosque conectado.

Un ejemplo de diagrama de árbol es aquel en el que cada una de las cuatro líneas externas termina en una X. Otra es cuando tres líneas externas terminan en una X , y la media línea restante se une con otra X , y las medias líneas restantes de esta X desembocan en líneas externas. Todos estos son también diagramas de bosque (ya que cada árbol es un bosque); un ejemplo de un bosque que no es un árbol es cuando ocho líneas externas terminan en dos X.

Es fácil comprobar que en todos estos casos, los momentos en todas las rectas internas están determinados por los momentos externos y la condición de conservación del momento en cada vértice.

Un diagrama que no es un diagrama de bosque se llama diagrama de bucle , y un ejemplo es aquel en el que dos líneas de una X se unen a líneas externas, mientras que las dos líneas restantes se unen entre sí. Las dos rectas unidas entre sí pueden tener cualquier momento, ya que ambas entran y salen del mismo vértice. Un ejemplo más complicado es aquel en el que dos X se unen entre sí haciendo coincidir las patas entre sí. Este diagrama no tiene líneas externas en absoluto.

La razón por la que los diagramas de bucles se llaman diagramas de bucles es porque el número de k -integrales que quedan indeterminadas por la conservación del momento es igual al número de bucles cerrados independientes en el diagrama, donde los bucles independientes se cuentan como en la teoría de la homología . La homología tiene un valor real (en realidad tiene un valor R ^d ), el valor asociado con cada línea es el impulso. El operador de límite lleva cada línea a la suma de los vértices finales con un signo positivo en la cabeza y un signo negativo en la cola. La condición de que se conserve el impulso es exactamente la condición de que el límite del gráfico ponderado con valor k sea cero.

Un conjunto de valores k válidos se puede redefinir arbitrariamente siempre que exista un circuito cerrado. Un circuito cerrado es un camino cíclico de vértices adyacentes que nunca vuelve a visitar el mismo vértice. Tal ciclo puede considerarse como el límite de una hipotética celda de 2. Los k -etiquetados de un gráfico que conserva el impulso (es decir, que tiene límite cero) hasta redefiniciones de k (es decir, hasta límites de 2 celdas) definen la primera homología de un gráfico. El número de momentos independientes que no están determinados es entonces igual al número de bucles de homología independientes. Para muchos gráficos, esto es igual al número de bucles contados de la forma más intuitiva.

Factores de simetría

El número de formas de formar un diagrama de Feynman dado uniendo medias líneas es grande y, según el teorema de Wick, cada forma de emparejar las medias líneas contribuye por igual. A menudo, esto cancela completamente los factoriales en el denominador de cada término, pero a veces la cancelación es incompleta.

El denominador no cancelado se llama factor de simetría del diagrama. La contribución de cada diagrama a la función de correlación debe dividirse por su factor de simetría.

Por ejemplo, considere el diagrama de Feynman formado por dos líneas externas unidas a una X y las dos medias líneas restantes de la X unidas entre sí. Hay 4 × 3 formas de unir las medias líneas externas a la X , y luego solo hay una forma de unir las dos líneas restantes entre sí. ¡ La X viene dividida entre 4! = 4 × 3 × 2 , pero el número de formas de unir las medias líneas X para hacer el diagrama es solo 4 × 3, por lo que la contribución de este diagrama se divide por dos.

Para otro ejemplo, considere el diagrama formado al unir todas las medias líneas de una X con todas las medias líneas de otra X. Este diagrama se llama burbuja de vacío porque no está conectado a ninguna línea externa. ¡Hay 4! formas de formar este diagrama, ¡pero el denominador incluye un 2! (de la expansión de la exponencial, hay dos X s) y dos factores de 4!. La contribución se multiplica por4!/¡2×4! ×4!= 1/48.

Otro ejemplo es el diagrama de Feynman formado por dos X donde cada X une hasta dos líneas externas y las dos medias líneas restantes de cada X están unidas entre sí. El número de formas de vincular una X a dos líneas externas es 4 × 3, y cualquiera de las X podría vincularse a cualquier par, lo que da un factor adicional de 2. Las dos medias líneas restantes en las dos X se pueden vincular a cada una de ellas. otro de dos maneras, de modo que el número total de formas de formar el diagrama es 4 × 3 × 4 × 3 × 2 × 2 , ¡mientras que el denominador es 4! ×4! ×2! . El factor de simetría total es 2 y la contribución de este diagrama se divide por 2.

El teorema del factor de simetría da el factor de simetría para un diagrama general: la contribución de cada diagrama de Feynman debe dividirse por el orden de su grupo de automorfismos, el número de simetrías que tiene.

Un automorfismo de un gráfico de Feynman es una permutación M de las líneas y una permutación N de los vértices con las siguientes propiedades:

1. Si una línea l va del vértice v al vértice v′ , entonces M ( l ) va de N ( v ) a N ( v′ ) . Si la línea no está dirigida, como lo es para un campo escalar real, entonces M ( l ) también puede ir de N ( v′ ) a N ( v ) .
2. Si una línea l termina en una línea externa, M ( l ) termina en la misma línea externa.
3. Si hay diferentes tipos de líneas, M ( l ) debe preservar el tipo.

Este teorema tiene una interpretación en términos de trayectorias de partículas: cuando están presentes partículas idénticas, la integral sobre todas las partículas intermedias no debe contar dos veces los estados que difieren sólo por el intercambio de partículas idénticas.

Prueba: Para probar este teorema, etiquete todas las líneas internas y externas de un diagrama con un nombre único. Luego forma el diagrama vinculando una media línea a un nombre y luego a la otra media línea.

Ahora cuenta el número de formas de formar el diagrama nombrado. Cada permutación de las X da un patrón diferente de vincular nombres a medias líneas, y este es un factor de n ! . Cada permutación de las medias líneas en una sola X da un factor de 4!. Por lo tanto, un diagrama con nombre se puede formar exactamente de tantas maneras como el denominador de la expansión de Feynman.

Pero el número de diagramas sin nombre es menor que el número de diagramas con nombre según el orden del grupo de automorfismos del gráfico.

Diagramas conectados: teorema del conglomerado vinculado

En términos generales, un diagrama de Feynman se denomina conectado si todos los vértices y líneas propagadoras están unidos por una secuencia de vértices y propagadores del diagrama mismo. Si lo vemos como un gráfico no dirigido, está conectado. La notable relevancia de tales diagramas en QFT se debe al hecho de que son suficientes para determinar la función de partición cuántica Z [ J ] . Más precisamente, los diagramas de Feynman conectados determinan

${\displaystyle iW[J]\equiv \ln Z[J].}$

Para ver esto, hay que recordar que

${\displaystyle Z[J]\propto \sum _{k}{D_{k}}}$

con D _k construido a partir de algún diagrama de Feynman (arbitrario) que se puede pensar que consta de varios componentes conectados C _i . Si uno encuentra n _i copias (idénticas) de un componente Ci dentro del diagrama de Feynman D _{k ,} debe incluir un factor de simetría n _i ! . Sin embargo, al final cada contribución de un diagrama de Feynman D _k a la función de partición tiene la forma genérica

${\displaystyle \prod _{i}{\frac {C_{i}^{n_{i}}}{n_{i}!}}}$

donde i etiqueta los (infinitos) diagramas de Feynman conectados posibles.

Un esquema para crear sucesivamente tales contribuciones desde D _k hasta Z [ J ] se obtiene mediante

${\displaystyle \left({\frac {1}{0!}}+{\frac {C_{1}}{1!}}+{\frac {C_{1}^{2}}{2!}}+\cdots \right)\left(1+C_{2}+{\frac {1}{2}}C_{2}^{2}+\cdots \right)\cdots }$

y por lo tanto rinde

${\displaystyle Z[J]\propto \prod _{i}{\sum _{n_{i}=0}^{\infty }{\frac {C_{i}^{n_{i}}}{n_{i}!}}}=\exp {\sum _{i}{C_{i}}}\propto \exp {W[J]}\,.}$

Para establecer la normalización Z ₀ = exp W [0] = 1 simplemente se calculan todos los diagramas de vacío conectados , es decir, los diagramas sin ninguna fuente J (a veces denominados tramos externos de un diagrama de Feynman).

Burbujas de vacío

Una consecuencia inmediata del teorema de los conglomerados vinculados es que todas las burbujas de vacío, diagramas sin líneas externas, se cancelan al calcular las funciones de correlación. Una función de correlación viene dada por una relación de integrales de ruta:

${\displaystyle \left\langle \phi _{1}(x_{1})\cdots \phi _{n}(x_{n})\right\rangle ={\frac {\displaystyle \int e^{-S}\phi _{1}(x_{1})\cdots \phi _{n}(x_{n})\,D\phi }{\displaystyle \int e^{-S}\,D\phi }}\,.}$

La parte superior es la suma de todos los diagramas de Feynman, incluidos los diagramas desconectados que no se conectan en absoluto con líneas externas. En cuanto a los diagramas conectados, el numerador incluye las mismas contribuciones de burbujas de vacío que el denominador:

${\displaystyle \int e^{-S}\phi _{1}(x_{1})\cdots \phi _{n}(x_{n})\,D\phi =\left(\sum E_{i}\right)\left(\exp \left(\sum _{i}C_{i}\right)\right)\,.}$

Donde la suma de los diagramas E incluye solo aquellos diagramas cuyos componentes conectados terminan en al menos una línea externa. Las burbujas de vacío son las mismas independientemente de las líneas externas y dan un factor multiplicativo general. El denominador es la suma de todas las burbujas de vacío, y al dividir se elimina el segundo factor.

Las burbujas de vacío entonces sólo son útiles para determinar el propio Z , que según la definición de la integral de trayectoria es igual a:

${\displaystyle Z=\int e^{-S}D\phi =e^{-HT}=e^{-\rho V}}$

donde ρ es la densidad de energía en el vacío. Cada burbuja de vacío contiene un factor de δ ( k ) que pone a cero el total k en cada vértice, y cuando no hay líneas externas, esto contiene un factor de δ (0) , porque la conservación del momento se aplica excesivamente. En volumen finito, este factor puede identificarse como el volumen total del espacio-tiempo. Dividiendo por el volumen, la integral restante de la burbuja de vacío tiene una interpretación: es una contribución a la densidad de energía del vacío.

Fuentes

Las funciones de correlación son la suma de los diagramas de Feynman conectados, pero el formalismo trata los diagramas conectados y desconectados de manera diferente. Las líneas internas terminan en los vértices, mientras que las líneas externas terminan en las inserciones. La introducción de fuentes unifica el formalismo, al crear nuevos vértices donde puede terminar una línea.

Las fuentes son campos externos, campos que contribuyen a la acción, pero no son variables dinámicas. Una fuente de campo escalar es otro campo escalar h que aporta un término al lagrangiano (de Lorentz):

${\displaystyle \int h(x)\phi (x)\,d^{d}x=\int h(k)\phi (k)\,d^{d}k\,}$

En la expansión de Feynman, esto aporta términos H con una media línea que termina en un vértice. Las líneas en un diagrama de Feynman ahora pueden terminar en un vértice X o en un vértice H , y solo una línea ingresa a un vértice H. La regla de Feynman para un vértice H es que una línea que parte de un H con impulso k obtiene un factor de h ( k ) .

La suma de los diagramas conexos en presencia de fuentes incluye un término para cada diagrama conexo en ausencia de fuentes, excepto que ahora los diagramas pueden terminar en la fuente. Tradicionalmente, una fuente se representa con una pequeña "×" con una línea que se extiende, exactamente como una inserción.

${\displaystyle \log {\big (}Z[h]{\big )}=\sum _{n,C}h(k_{1})h(k_{2})\cdots h(k_{n})C(k_{1},\cdots ,k_{n})\,}$

donde C ( k ₁ ,..., k _n ) es el diagrama conectado con n líneas externas que transportan impulso como se indica. La suma se realiza sobre todos los diagramas conectados, como antes.

El campo h no es dinámico, lo que significa que no existe una integral de trayectoria sobre h : h es sólo un parámetro en el lagrangiano, que varía de un punto a otro. La integral de trayectoria para el campo es:

${\displaystyle Z[h]=\int e^{iS+i\int h\phi }\,D\phi \,}$

y es función de los valores de h en cada punto. Una forma de interpretar esta expresión es tomando la transformada de Fourier en el espacio de campo. Si hay una densidad de probabilidad en R ⁿ , la transformada de Fourier de la densidad de probabilidad es:

${\displaystyle \int \rho (y)e^{iky}\,d^{n}y=\left\langle e^{iky}\right\rangle =\left\langle \prod _{i=1}^{n}e^{ih_{i}y_{i}}\right\rangle \,}$

La transformada de Fourier es la expectativa de una exponencial oscilatoria. La integral de trayectoria en presencia de una fuente h ( x ) es:

${\displaystyle Z[h]=\int e^{iS}e^{i\int _{x}h(x)\phi (x)}\,D\phi =\left\langle e^{ih\phi }\right\rangle }$

que, en una red, es el producto de una exponencial oscilatoria para cada valor de campo:

${\displaystyle \left\langle \prod _{x}e^{ih_{x}\phi _{x}}\right\rangle }$

La transformada de Fourier de una función delta es una constante, que da una expresión formal para una función delta:

${\displaystyle \delta (x-y)=\int e^{ik(x-y)}\,dk}$

Esto le indica cómo se ve una función delta de campo en una integral de ruta. Para dos campos escalares φ y η ,

${\displaystyle \delta (\phi -\eta )=\int e^{ih(x){\big (}\phi (x)-\eta (x){\big )}\,d^{d}x}\,Dh\,,}$

que se integra sobre la coordenada de transformada de Fourier, sobre h . Esta expresión es útil para cambiar formalmente las coordenadas de campo en la integral de trayectoria, de la misma manera que se usa una función delta para cambiar las coordenadas en una integral multidimensional ordinaria.

La función de partición ahora es una función del campo h , y la función de partición física es el valor cuando h es la función cero:

Las funciones de correlación son derivadas de la integral de trayectoria con respecto a la fuente:

${\displaystyle \left\langle \phi (x)\right\rangle ={\frac {1}{Z}}{\frac {\partial }{\partial h(x)}}Z[h]={\frac {\partial }{\partial h(x)}}\log {\big (}Z[h]{\big )}\,.}$

En el espacio euclidiano, las contribuciones de las fuentes a la acción aún pueden aparecer con un factor de i , por lo que aún realizan una transformada de Fourier.

Girar1/2; "fotones" y "fantasmas"

Girar1/2: Integrales de Grassmann

La integral de trayectoria de campo se puede extender al caso de Fermi, pero sólo si se amplía la noción de integración. Una integral de Grassmann de un campo de Fermi libre es un determinante de alta dimensión o Pfaffiano , que define el nuevo tipo de integración gaussiana apropiada para los campos de Fermi.

Las dos fórmulas fundamentales de la integración de Grassmann son:

${\displaystyle \int e^{M_{ij}{\bar {\psi }}^{i}\psi ^{j}}\,D{\bar {\psi }}\,D\psi =\mathrm {Det} (M)\,,}$

donde M es una matriz arbitraria y ψ , ψ son variables de Grassmann independientes para cada índice i , y

${\displaystyle \int e^{{\frac {1}{2}}A_{ij}\psi ^{i}\psi ^{j}}\,D\psi =\mathrm {Pfaff} (A)\,,}$

donde A es una matriz antisimétrica, ψ es una colección de variables de Grassmann y la1/2es evitar el doble conteo (ya que ψ ⁱ ψ ^j = − ψ ^j ψ ⁱ ).

En notación matricial, donde ψ y η son vectores fila con valores de Grassmann, η y ψ son vectores columna con valores de Grassmann y M es una matriz con valores reales:

${\displaystyle Z=\int e^{{\bar {\psi }}M\psi +{\bar {\eta }}\psi +{\bar {\psi }}\eta }\,D{\bar {\psi }}\,D\psi =\int e^{\left({\bar {\psi }}+{\bar {\eta }}M^{-1}\right)M\left(\psi +M^{-1}\eta \right)-{\bar {\eta }}M^{-1}\eta }\,D{\bar {\psi }}\,D\psi =\mathrm {Det} (M)e^{-{\bar {\eta }}M^{-1}\eta }\,,}$

donde la última igualdad es consecuencia de la invariancia de traslación de la integral de Grassmann. Las variables de Grassmann η son fuentes externas para ψ , y diferenciar con respecto a η reduce los factores de ψ .

${\displaystyle \left\langle {\bar {\psi }}\psi \right\rangle ={\frac {1}{Z}}{\frac {\partial }{\partial \eta }}{\frac {\partial }{\partial {\bar {\eta }}}}Z|_{\eta ={\bar {\eta }}=0}=M^{-1}}$

nuevamente, en una notación matricial esquemática. El significado de la fórmula anterior es que la derivada con respecto al componente apropiado de η y η da el elemento matricial de M ⁻¹ . Esto es exactamente análogo a la fórmula de integración de trayectoria bosónica para una integral gaussiana de un campo bosónico complejo:

${\displaystyle \int e^{\phi ^{*}M\phi +h^{*}\phi +\phi ^{*}h}\,D\phi ^{*}\,D\phi ={\frac {e^{h^{*}M^{-1}h}}{\mathrm {Det} (M)}}}$

${\displaystyle \left\langle \phi ^{*}\phi \right\rangle ={\frac {1}{Z}}{\frac {\partial }{\partial h}}{\frac {\partial }{\partial h^{*}}}Z|_{h=h^{*}=0}=M^{-1}\,.}$

De modo que el propagador es la inversa de la matriz en la parte cuadrática de la acción tanto en el caso de Bose como en el de Fermi.

Para los campos reales de Grassmann, para los fermiones de Majorana , la integral de trayectoria es una forma pfaffiana multiplicada por una forma cuadrática fuente, y las fórmulas dan la raíz cuadrada del determinante, tal como lo hacen para los campos bosónicos reales. El propagador sigue siendo el inverso de la parte cuadrática.

El Lagrangiano de Dirac libre:

${\displaystyle \int {\bar {\psi }}\left(\gamma ^{\mu }\partial _{\mu }-m\right)\psi }$

da formalmente las ecuaciones de movimiento y las relaciones de anticonmutación del campo de Dirac, tal como el Lagrangiano de Klein Gordon en una integral de trayectoria ordinaria da las ecuaciones de movimiento y las relaciones de conmutación del campo escalar. Al utilizar la transformada espacial de Fourier del campo de Dirac como nueva base para el álgebra de Grassmann, la parte cuadrática de la acción de Dirac resulta sencilla de invertir:

${\displaystyle S=\int _{k}{\bar {\psi }}\left(i\gamma ^{\mu }k_{\mu }-m\right)\psi \,.}$

El propagador es el inverso de la matriz M que une ψ ( k ) y ψ ( k ) , ya que diferentes valores de k no se mezclan.

${\displaystyle \left\langle {\bar {\psi }}(k')\psi (k)\right\rangle =\delta (k+k'){\frac {1}{\gamma \cdot k-m}}=\delta (k+k'){\frac {\gamma \cdot k+m}{k^{2}-m^{2}}}}$

El análogo del teorema de Wick hace coincidir ψ y ψ en pares:

${\displaystyle \left\langle {\bar {\psi }}(k_{1}){\bar {\psi }}(k_{2})\cdots {\bar {\psi }}(k_{n})\psi (k'_{1})\cdots \psi (k_{n})\right\rangle =\sum _{\mathrm {pairings} }(-1)^{S}\prod _{\mathrm {pairs} \;i,j}\delta \left(k_{i}-k_{j}\right){\frac {1}{\gamma \cdot k_{i}-m}}}$

donde S es el signo de la permutación que reordena la secuencia de ψ y ψ para colocar las que están emparejadas para formar las funciones delta una al lado de la otra, con la ψ justo antes de la ψ . Dado que un par ψ , ψ es un elemento conmutador del álgebra de Grassmann, no importa en qué orden estén los pares. Si más de un par ψ , ψ tienen el mismo k , la integral es cero y es fácil de verificar que la suma de los pares da cero en este caso (siempre hay un número par de ellos). Este es el análogo de Grassmann de los momentos gaussianos superiores que completaron anteriormente el teorema de Bosonic Wick.

Las reglas para girar1/2Las partículas de Dirac son las siguientes: el propagador es el inverso del operador de Dirac, las líneas tienen flechas como en un campo escalar complejo y el diagrama adquiere un factor general de −1 para cada bucle cerrado de Fermi. Si hay un número impar de bucles de Fermi, el diagrama cambia de signo. Históricamente, la regla −1 fue muy difícil de descubrir para Feynman. Lo descubrió tras un largo proceso de prueba y error, ya que carecía de una teoría adecuada de la integración de Grassmann.

La regla se deriva de la observación de que el número de rectas de Fermi en un vértice es siempre par. Cada término en lagrangiano siempre debe ser bosónico. Un bucle de Fermi se cuenta siguiendo líneas fermiónicas hasta que uno regresa al punto inicial y luego elimina esas líneas del diagrama. Repetir este proceso eventualmente borra todas las líneas fermiónicas: este es el algoritmo de Euler para colorear un gráfico en 2 colores, que funciona siempre que cada vértice tenga un grado par. El número de pasos en el algoritmo de Euler sólo es igual al número de ciclos de homología fermiónica independientes en el caso especial común de que todos los términos del lagrangiano son exactamente cuadráticos en los campos de Fermi, de modo que cada vértice tiene exactamente dos líneas fermiónicas. Cuando hay cuatro interacciones de Fermi (como en la teoría efectiva de Fermi de las interacciones nucleares débiles ), hay más integrales k que bucles de Fermi. En este caso, la regla de conteo debe aplicar el algoritmo de Euler emparejando las líneas de Fermi en cada vértice en pares que juntos forman un factor bosónico del término en lagrangiano, y al ingresar a un vértice por una línea, el algoritmo siempre debe dejar con la línea asociada.

Para aclarar y probar la regla, consideremos un diagrama de Feynman formado a partir de vértices, términos en lagrangiano, con campos de Fermión. El término completo es bosónico, es un elemento conmutador del álgebra de Grassmann, por lo que el orden en que aparecen los vértices no es importante. Las líneas de Fermi están vinculadas en bucles y, al atravesar el bucle, se pueden reordenar los términos de los vértices uno tras otro a medida que se recorre sin ningún coste de signo. La excepción es cuando regresa al punto de partida y la media línea final debe unirse con la primera media línea no vinculada. Esto requiere una permutación para mover el último ψ para que vaya delante del primer ψ , y esto da el signo.

Esta regla es el único efecto visible del principio de exclusión en líneas internas. Cuando hay líneas externas, las amplitudes son antisimétricas cuando se intercambian dos inserciones de Fermi para partículas idénticas. Esto es automático en el formalismo de fuentes, porque las fuentes de los campos de Fermi son en sí mismas valoradas por Grassmann.

Giro 1: fotones

El propagador ingenuo de fotones es infinito, ya que el lagrangiano para el campo A es:

${\displaystyle S=\int {\tfrac {1}{4}}F^{\mu \nu }F_{\mu \nu }=\int -{\tfrac {1}{2}}\left(\partial ^{\mu }A_{\nu }\partial _{\mu }A^{\nu }-\partial ^{\mu }A_{\mu }\partial _{\nu }A^{\nu }\right)\,.}$

La forma cuadrática que define al propagador no es invertible. La razón es la invariancia de calibre del campo; agregar un gradiente a A no cambia la física.

Para solucionar este problema, es necesario arreglar un medidor. La forma más conveniente es exigir que la divergencia de A sea alguna función f cuyo valor sea aleatorio de un punto a otro. No hace daño integrar los valores de f , ya que solo determina la elección del calibre. Este procedimiento inserta el siguiente factor en la integral de trayectoria para A :

${\displaystyle \int \delta \left(\partial _{\mu }A^{\mu }-f\right)e^{-{\frac {f^{2}}{2}}}\,Df\,.}$

El primer factor, la función delta, fija el calibre. El segundo factor suma diferentes valores de f que son fijaciones de calibre no equivalentes. esto es simplemente

${\displaystyle e^{-{\frac {\left(\partial _{\mu }A_{\mu }\right)^{2}}{2}}}\,.}$

La contribución adicional de la fijación del ancho de vía cancela la segunda mitad del Lagrangiano libre, dando al Lagrangiano de Feynman:

${\displaystyle S=\int \partial ^{\mu }A^{\nu }\partial _{\mu }A_{\nu }}$

que es como cuatro campos escalares libres e independientes, uno para cada componente de A. El propagador de Feynman es:

${\displaystyle \left\langle A_{\mu }(k)A_{\nu }(k')\right\rangle =\delta \left(k+k'\right){\frac {g_{\mu \nu }}{k^{2}}}.}$

La única diferencia es que el signo de un propagador es incorrecto en el caso de Lorentz: el componente temporal tiene un propagador de signo opuesto. Esto significa que estos estados de partículas tienen una norma negativa: no son estados físicos. En el caso de los fotones, es fácil mostrar mediante métodos de diagramas que estos estados no son físicos: su contribución se cancela con los fotones longitudinales para dejar solo dos contribuciones físicas de polarización de fotones para cualquier valor de k .

Si el promedio sobre f se realiza con un coeficiente diferente de1/2, los dos términos no se cancelan por completo. Esto da un lagrangiano covariante con un coeficiente , que no afecta en nada: ${\displaystyle \lambda }$

${\displaystyle S=\int {\tfrac {1}{2}}\left(\partial ^{\mu }A^{\nu }\partial _{\mu }A_{\nu }-\lambda \left(\partial _{\mu }A^{\mu }\right)^{2}\right)}$

y el propagador covariante de QED es:

${\displaystyle \left\langle A_{\mu }(k)A_{\nu }(k')\right\rangle =\delta \left(k+k'\right){\frac {g_{\mu \nu }-\lambda {\frac {k_{\mu }k_{\nu }}{k^{2}}}}{k^{2}}}.}$

Giro 1: fantasmas no abelianos

Para encontrar las reglas de Feynman para campos de calibre no abelianos, el procedimiento que realiza la fijación del calibre debe corregirse cuidadosamente para tener en cuenta un cambio de variables en la integral de trayectoria.

El factor de fijación del calibre tiene un determinante adicional al hacer estallar la función delta:

${\displaystyle \delta \left(\partial _{\mu }A_{\mu }-f\right)e^{-{\frac {f^{2}}{2}}}\det M}$

Para encontrar la forma del determinante, considere primero una integral bidimensional simple de una función f que depende sólo de r , no del ángulo θ . Insertando una integral sobre θ :

${\displaystyle \int f(r)\,dx\,dy=\int f(r)\int d\theta \,\delta (y)\left|{\frac {dy}{d\theta }}\right|\,dx\,dy}$

El factor derivado asegura que al hacer estallar la función delta en θ se elimina la integral. Cambiando el orden de integración,

${\displaystyle \int f(r)\,dx\,dy=\int d\theta \,\int f(r)\delta (y)\left|{\frac {dy}{d\theta }}\right|\,dx\,dy}$

pero ahora la función delta se puede insertar en y ,

${\displaystyle \int f(r)\,dx\,dy=\int d\theta _{0}\,\int f(x)\left|{\frac {dy}{d\theta }}\right|\,dx\,.}$

La integral sobre θ simplemente da un factor general de 2 π , mientras que la tasa de cambio de y con un cambio en θ es solo x , por lo que este ejercicio reproduce la fórmula estándar para la integración polar de una función radial:

${\displaystyle \int f(r)\,dx\,dy=2\pi \int f(x)x\,dx}$

En la integral de trayectoria para un campo de calibre no abeliano, la manipulación análoga es:

${\displaystyle \int DA\int \delta {\big (}F(A){\big )}\det \left({\frac {\partial F}{\partial G}}\right)\,DGe^{iS}=\int DG\int \delta {\big (}F(A){\big )}\det \left({\frac {\partial F}{\partial G}}\right)e^{iS}\,}$

El factor de delante es el volumen del grupo medidor y aporta una constante que puede descartarse. La integral restante está sobre la acción fija del calibre.

${\displaystyle \int \det \left({\frac {\partial F}{\partial G}}\right)e^{iS_{GF}}\,DA\,}$

Para obtener un indicador covariante, la condición de fijación del indicador es la misma que en el caso abeliano:

${\displaystyle \partial _{\mu }A^{\mu }=f\,,}$

Cuya variación bajo una transformación de calibre infinitesimal viene dada por:

${\displaystyle \partial _{\mu }\,D_{\mu }\alpha \,,}$

donde α es el elemento valorado adjunto del álgebra de Lie en cada punto que realiza la transformación de calibre infinitesimal. Esto añade el determinante de Faddeev Popov a la acción:

${\displaystyle \det \left(\partial _{\mu }\,D_{\mu }\right)\,}$

que puede reescribirse como una integral de Grassmann introduciendo campos fantasma:

${\displaystyle \int e^{{\bar {\eta }}\partial _{\mu }\,D^{\mu }\eta }\,D{\bar {\eta }}\,D\eta \,}$

El determinante es independiente de f , por lo que la integral de ruta sobre f puede dar el propagador de Feynman (o un propagador covariante) eligiendo la medida para f como en el caso abeliano. La acción fija de calibre completo es entonces la acción de Yang Mills en calibre Feynman con una acción fantasma adicional:

${\displaystyle S=\int \operatorname {Tr} \partial _{\mu }A_{\nu }\partial ^{\mu }A^{\nu }+f_{jk}^{i}\partial ^{\nu }A_{i}^{\mu }A_{\mu }^{j}A_{\nu }^{k}+f_{jr}^{i}f_{kl}^{r}A_{i}A_{j}A^{k}A^{l}+\operatorname {Tr} \partial _{\mu }{\bar {\eta }}\partial ^{\mu }\eta +{\bar {\eta }}A_{j}\eta \,}$

Los diagramas se derivan de esta acción. El propagador de los campos spin-1 tiene la forma habitual de Feynman. Hay vértices de grado 3 con factores de momento cuyos acoplamientos son las constantes de estructura, y vértices de grado 4 cuyos acoplamientos son productos de constantes de estructura. Hay bucles fantasma adicionales, que cancelan los estados longitudinales y temporales en los bucles A.

En el caso abeliano, el determinante de las medidas covariantes no depende de A , por lo que los fantasmas no contribuyen a los diagramas conectados.

Representación del camino de las partículas

Los diagramas de Feynman fueron descubiertos originalmente por Feynman, mediante prueba y error, como una forma de representar la contribución a la matriz S de diferentes clases de trayectorias de partículas.

Representación de Schwinger

El propagador escalar euclidiano tiene una sugerente representación:

${\displaystyle {\frac {1}{p^{2}+m^{2}}}=\int _{0}^{\infty }e^{-\tau \left(p^{2}+m^{2}\right)}\,d\tau }$

El significado de esta identidad (que es una integración elemental) se aclara con la transformación de Fourier al espacio real.

${\displaystyle \Delta (x)=\int _{0}^{\infty }d\tau e^{-m^{2}\tau }{\frac {1}{({4\pi \tau })^{d/2}}}e^{\frac {-x^{2}}{4\tau }}}$

La contribución en cualquier valor de τ al propagador es una gaussiana de ancho √ τ . La función de propagación total de 0 a x es una suma ponderada sobre todos los tiempos adecuados τ de un gaussiano normalizado, la probabilidad de terminar en x después de un recorrido aleatorio de tiempo τ .

La representación integral de ruta para el propagador es entonces:

${\displaystyle \Delta (x)=\int _{0}^{\infty }d\tau \int DX\,e^{-\int \limits _{0}^{\tau }\left({\frac {{\dot {x}}^{2}}{2}}+m^{2}\right)d\tau '}}$

que es una reescritura de ruta integral de la representación de Schwinger .

La representación de Schwinger es útil para poner de manifiesto el aspecto de partículas del propagador y para simetrizar denominadores de diagramas de bucles.

Combinando denominadores

La representación de Schwinger tiene una aplicación práctica inmediata a los diagramas de bucles. Por ejemplo, para el diagrama de la teoría φ ⁴ formado al unir dos x s en dos medias líneas y hacer que las líneas restantes sean externas, la integral sobre los propagadores internos en el bucle es:

${\displaystyle \int _{k}{\frac {1}{k^{2}+m^{2}}}{\frac {1}{(k+p)^{2}+m^{2}}}\,.}$

Aquí una línea lleva impulso k y la otra k + p . La asimetría se puede solucionar poniendo todo en la representación de Schwinger.

${\displaystyle \int _{t,t'}e^{-t(k^{2}+m^{2})-t'\left((k+p)^{2}+m^{2}\right)}\,dt\,dt'\,.}$

Ahora el exponente depende principalmente de t + t ′ ,

${\displaystyle \int _{t,t'}e^{-(t+t')(k^{2}+m^{2})-t'2p\cdot k-t'p^{2}}\,,}$

excepto por el poquito asimétrico. Definiendo la variable u = t + t ′ y v =t ′/tu, la variable u va de 0 a ∞ , mientras que v va de 0 a 1. La variable u es el tiempo propio total para el ciclo, mientras que v parametriza la fracción del tiempo propio en la parte superior del ciclo versus la parte inferior.

El jacobiano para esta transformación de variables es fácil de calcular a partir de las identidades:

${\displaystyle d(uv)=dt'\quad du=dt+dt'\,,}$

y " cuñando " da

${\displaystyle u\,du\wedge dv=dt\wedge dt'\,}$.

Esto permite evaluar explícitamente la integral u :

${\displaystyle \int _{u,v}ue^{-u\left(k^{2}+m^{2}+v2p\cdot k+vp^{2}\right)}=\int {\frac {1}{\left(k^{2}+m^{2}+v2p\cdot k-vp^{2}\right)^{2}}}\,dv}$

dejando sólo la integral v . Este método, inventado por Schwinger pero generalmente atribuido a Feynman, se llama denominador combinatorio . De manera abstracta, es la identidad elemental:

${\displaystyle {\frac {1}{AB}}=\int _{0}^{1}{\frac {1}{{\big (}vA+(1-v)B{\big )}^{2}}}\,dv}$

Pero esta forma no proporciona la motivación física para introducir v ; v es la proporción de tiempo propio en uno de los tramos del bucle.

Una vez que se combinan los denominadores, un cambio de k a k ′ = k + vp simetriza todo:

${\displaystyle \int _{0}^{1}\int {\frac {1}{\left(k^{2}+m^{2}+2vp\cdot k+vp^{2}\right)^{2}}}\,dk\,dv=\int _{0}^{1}\int {\frac {1}{\left(k'^{2}+m^{2}+v(1-v)p^{2}\right)^{2}}}\,dk'\,dv}$

Esta forma muestra que en el momento en que p ² es más negativo que cuatro veces la masa de la partícula en el bucle, lo que sucede en una región física del espacio de Lorentz , la integral tiene un corte. Aquí es exactamente cuando el impulso externo puede crear partículas físicas.

Cuando el bucle tiene más vértices, hay más denominadores para combinar:

${\displaystyle \int dk\,{\frac {1}{k^{2}+m^{2}}}{\frac {1}{(k+p_{1})^{2}+m^{2}}}\cdots {\frac {1}{(k+p_{n})^{2}+m^{2}}}}$

La regla general se desprende de la prescripción de Schwinger para n + 1 denominadores:

${\displaystyle {\frac {1}{D_{0}D_{1}\cdots D_{n}}}=\int _{0}^{\infty }\cdots \int _{0}^{\infty }e^{-u_{0}D_{0}\cdots -u_{n}D_{n}}\,du_{0}\cdots du_{n}\,.}$

La integral sobre los parámetros de Schwinger u _i se puede dividir como antes en una integral sobre el tiempo propio total u = u ₀ + u ₁ ... + u _n y una integral sobre la fracción del tiempo propio en todos menos el primero. segmento del bucle v _i =tu _yo/tupara i ∈ {1,2,..., n } . Los v _i son positivos y suman menos de 1, de modo que la integral v es sobre un simplex de n dimensiones.

El jacobiano para la transformación de coordenadas se puede calcular como antes:

${\displaystyle du=du_{0}+du_{1}\cdots +du_{n}\,}$

${\displaystyle d(uv_{i})=du_{i}\,.}$

Juntando todas estas ecuaciones se obtiene

${\displaystyle u^{n}\,du\wedge dv_{1}\wedge dv_{2}\cdots \wedge dv_{n}=du_{0}\wedge du_{1}\cdots \wedge du_{n}\,.}$

Esto da la integral:

${\displaystyle \int _{0}^{\infty }\int _{\mathrm {simplex} }u^{n}e^{-u\left(v_{0}D_{0}+v_{1}D_{1}+v_{2}D_{2}\cdots +v_{n}D_{n}\right)}\,dv_{1}\cdots dv_{n}\,du\,,}$

donde el simplex es la región definida por las condiciones

${\displaystyle v_{i}>0\quad {\mbox{and}}\quad \sum _{i=1}^{n}v_{i}<1}$

así como

${\displaystyle v_{0}=1-\sum _{i=1}^{n}v_{i}\,.}$

Realizar la integral u proporciona la prescripción general para combinar denominadores:

${\displaystyle {\frac {1}{D_{0}\cdots D_{n}}}=n!\int _{\mathrm {simplex} }{\frac {1}{\left(v_{0}D_{0}+v_{1}D_{1}\cdots +v_{n}D_{n}\right)^{n+1}}}\,dv_{1}\,dv_{2}\cdots dv_{n}}$

Dado que el numerador del integrando no está involucrado, la misma prescripción funciona para cualquier bucle, sin importar los espines que lleven las piernas. La interpretación de los parámetros _vi es que son la fracción del tiempo total propio empleado en cada pierna.

Dispersión

Las funciones de correlación de una teoría cuántica de campos describen la dispersión de partículas. La definición de "partícula" en la teoría relativista de campos no es evidente, porque si se intenta determinar la posición de modo que la incertidumbre sea menor que la longitud de onda de Compton , la incertidumbre en la energía es lo suficientemente grande como para producir más partículas y antipartículas de la misma. mismo tipo del vacío. Esto significa que la noción de un estado de una sola partícula es hasta cierto punto incompatible con la noción de un objeto localizado en el espacio.

En la década de 1930, Wigner dio una definición matemática de los estados de una sola partícula: son una colección de estados que forman una representación irreductible del grupo de Poincaré. Los estados de una sola partícula describen un objeto con una masa finita, un momento bien definido y un espín. Esta definición está bien para protones y neutrones, electrones y fotones, pero excluye a los quarks, que están confinados permanentemente, por lo que el punto de vista moderno es más complaciente: una partícula es cualquier cosa cuya interacción pueda describirse en términos de diagramas de Feynman, que tienen una interpretación como una suma de trayectorias de partículas.

Un operador de campo puede actuar para producir un estado de una partícula a partir del vacío, lo que significa que el operador de campo φ ( x ) produce una superposición de estados de partículas de Wigner. En la teoría del campo libre, el campo produce estados de una sola partícula. Pero cuando hay interacciones, el operador de campo también puede producir estados de 3 partículas, 5 partículas (si no hay simetría +/− también 2, 4, 6 partículas). Calcular la amplitud de dispersión para estados de partículas individuales solo requiere un límite cuidadoso, enviando los campos al infinito e integrando en el espacio para deshacerse de las correcciones de orden superior.

La relación entre las funciones de dispersión y correlación es el teorema LSZ: la amplitud de dispersión para que n partículas vayan a m partículas en un evento de dispersión está dada por la suma de los diagramas de Feynman que entran en la función de correlación para n + m inserciones de campo. , omitiendo los propagadores de las patas externas.

Por ejemplo, para la interacción λφ ⁴ de la sección anterior, la contribución de orden λ a la función de correlación (Lorentz) es:

${\displaystyle \left\langle \phi (k_{1})\phi (k_{2})\phi (k_{3})\phi (k_{4})\right\rangle ={\frac {i}{k_{1}^{2}}}{\frac {i}{k_{2}^{2}}}{\frac {i}{k_{3}^{2}}}{\frac {i}{k_{4}^{2}}}i\lambda \,}$

Eliminación de los propagadores externos, es decir, eliminación de los factores dei/k ², da la amplitud de dispersión invariante M :

${\displaystyle M=i\lambda \,}$

que es una constante, independiente del impulso entrante y saliente. La interpretación de la amplitud de dispersión es que la suma de | METRO | ² sobre todos los estados finales posibles es la probabilidad del evento de dispersión. Sin embargo, la normalización de los estados de una sola partícula debe elegirse cuidadosamente para garantizar que M sea un invariante relativista.

Los estados de partículas individuales no relativistas están etiquetados por el momento k y se eligen para que tengan la misma norma en cada valor de k . Esto se debe a que el operador unitario no relativista en estados de partículas individuales es:

${\displaystyle \int dk\,|k\rangle \langle k|\,.}$

En relatividad, la integral sobre los k -estados para una partícula de masa m se integra sobre una hipérbola en el espacio E , k definido por la relación energía-momento:

${\displaystyle E^{2}-k^{2}=m^{2}\,.}$

Si la integral pesa cada k punto por igual, la medida no es invariante de Lorentz. La medida invariante integra todos los valores de k y E , restringiéndose a la hipérbola con una función delta invariante de Lorentz:

${\displaystyle \int \delta (E^{2}-k^{2}-m^{2})|E,k\rangle \langle E,k|\,dE\,dk=\int {dk \over 2E}|k\rangle \langle k|\,.}$

Entonces los k -estados normalizados son diferentes de los k -estados relativistas normalizados por un factor de

${\displaystyle {\sqrt {E}}=\left(k^{2}-m^{2}\right)^{\frac {1}{4}}\,.}$

La amplitud invariante M es entonces la amplitud de probabilidad de que los estados entrantes relativistas normalizados se conviertan en estados salientes relativistas normalizados.

Para valores no relativistas de k , la normalización relativista es la misma que la normalización no relativista (hasta un factor constante √ m ). En este límite, la amplitud de dispersión invariante φ ⁴ sigue siendo constante. Las partículas creadas por el campo φ se dispersan en todas direcciones con igual amplitud.

El potencial no relativista, que se dispersa en todas direcciones con igual amplitud (en la aproximación de Born ), es aquel cuya transformada de Fourier es constante: un potencial de función delta. La dispersión de orden más bajo de la teoría revela la interpretación no relativista de esta teoría: describe una colección de partículas con una repulsión de función delta. Dos de estas partículas tienen aversión a ocupar el mismo punto al mismo tiempo.

Efectos no perturbativos

Al pensar en los diagramas de Feynman como una serie de perturbaciones , los efectos no perturbativos como el efecto túnel no aparecen, porque cualquier efecto que llegue a cero más rápido que cualquier polinomio no afecta la serie de Taylor. Incluso los estados ligados están ausentes, ya que en cualquier orden finito las partículas sólo se intercambian un número finito de veces, y para formar un estado ligado, la fuerza de unión debe durar para siempre.

Pero este punto de vista es engañoso, porque los diagramas no sólo describen la dispersión, sino que también son una representación de las correlaciones de la teoría de campos de corta distancia. Codifican no sólo procesos asintóticos como la dispersión de partículas, sino que también describen las reglas de multiplicación de campos y la expansión del producto del operador . Los procesos de túneles no perturbativos involucran configuraciones de campo que en promedio aumentan cuando la constante de acoplamiento se vuelve pequeña, pero cada configuración es una superposición coherente de partículas cuyas interacciones locales se describen mediante diagramas de Feynman. Cuando el acoplamiento es pequeño, estos se convierten en procesos colectivos que involucran una gran cantidad de partículas, pero donde la interacción entre cada una de las partículas es simple. ^{[ cita necesaria ]} (La serie de perturbaciones de cualquier teoría cuántica de campos interactuantes tiene un radio de convergencia cero , lo que complica el límite de la serie infinita de diagramas necesarios (en el límite del acoplamiento evanescente) para describir tales configuraciones de campo).

Esto significa que los efectos no perturbativos aparecen asintóticamente en resúmenes de infinitas clases de diagramas, y estos diagramas pueden ser localmente simples. Los gráficos determinan las ecuaciones locales de movimiento, mientras que las configuraciones a gran escala permitidas describen la física no perturbativa. Pero como los propagadores de Feynman no son locales en el tiempo, traducir un proceso de campo a un lenguaje de partículas coherente no es completamente intuitivo y sólo se ha elaborado explícitamente en ciertos casos especiales. En el caso de estados ligados no relativistas , la ecuación de Bethe-Salpeter describe la clase de diagramas que se incluyen para describir un átomo relativista. Para la cromodinámica cuántica , las reglas de suma de Shifman-Vainshtein-Zakharov describen modos de campo de longitud de onda larga excitados no perturbativamente en el lenguaje de partículas, pero solo de una manera fenomenológica.

El número de diagramas de Feynman en órdenes superiores de la teoría de la perturbación es muy grande, porque hay tantos diagramas como gráficos con un número determinado de nodos. Los efectos no perturbativos dejan una huella en la forma en que el número de diagramas y resúmenes divergen en orden superior. Sólo porque los efectos no perturbativos aparecen en forma oculta en los diagramas fue posible analizar los efectos no perturbativos en la teoría de cuerdas, donde en muchos casos la única descripción disponible es la de Feynman.

En la cultura popular

• El uso del diagrama anterior de la partícula virtual que produce un par quark - antiquark apareció en la comedia televisiva The Big Bang Theory , en el episodio "The Bat Jar Conjecture".
• PhD Comics del 11 de enero de 2012 muestra diagramas de Feynman que visualizan y describen interacciones académicas cuánticas , es decir, los caminos seguidos por Ph.D. estudiantes al interactuar con sus asesores. ^[11]
• Diagramas de vacío , una historia de ciencia ficción de Stephen Baxter , presenta el diagrama de vacío titular, un tipo específico de diagrama de Feynman.
• Feynman y su esposa, Gweneth Howarth, compraron un Dodge Tradesman Maxivan en 1975 y lo pintaron con diagramas de Feynman. ^[12] La furgoneta es actualmente propiedad del diseñador y físico de videojuegos Seamus Blackley . ^[13]

Ver también

• Diagrama de Feynman de un bucle
• Julian Schwinger#Schwinger y Feynman
• Interpretación de Stueckelberg-Feynman
• Diagrama de pingüino
• Formulación integral de camino
• Propagador
• Lista de diagramas de Feynman
• Diagramas de momento angular (mecánica cuántica)

Notas

1. "Fue la contribución de Dyson indicar cómo se podrían utilizar los conocimientos visuales de Feynman [...] Se dio cuenta de que los diagramas de Feynman [...] también pueden verse como una representación del contenido lógico de las teorías de campo (como se indica en su perturbativo expansiones)". Schweber, op.cit (1994)

Referencias

1. Káiser, David (2005). «Física y Diagramas de Feynman» (PDF) . Científico americano . 93 (2): 156. doi :10.1511/2005.52.957. Archivado (PDF) desde el original el 27 de mayo de 2012.
2. "Por qué los diagramas de Feynman son tan importantes". Revista Quanta . 5 de julio de 2016 . Consultado el 16 de junio de 2020 .
3. Feynman, Richard (1949). "La teoría de los positrones". Revisión física . 76 (6): 749–759. Código bibliográfico : 1949PhRv...76..749F. doi : 10.1103/PhysRev.76.749. S2CID  120117564. En esta solución, los 'estados de energía negativos' aparecen en una forma que puede representarse (como lo hace Stückelberg) en el espacio-tiempo como ondas que se alejan del potencial externo hacia atrás en el tiempo. Experimentalmente, tal onda corresponde a un positrón que se acerca al potencial y aniquila al electrón.
4. Penco, R.; Mauro, D. (2006). "Teoría de la perturbación mediante diagramas de Feynman en mecánica clásica". Revista Europea de Física . 27 (5): 1241-1250. arXiv : hep-th/0605061 . Código bibliográfico : 2006EJPh...27.1241P. doi :10.1088/0143-0807/27/5/023. S2CID  2895311.
5. George Johnson (julio de 2000). "El jaguar y el zorro". El Atlántico . Consultado el 26 de febrero de 2013 .
6. Gribbin, John; Gribbin, María (1997). "5". Richard Feynman: una vida en la ciencia . Pingüino-Putnam.
7. Mlodinow, Leonard (2011). El arcoíris de Feynman . Antiguo. pag. 29.
8. Gerardus 't Hooft, Martinus Veltman, Diagrammar , CERN Yellow Report 1973, reimpreso en G. 't Hooft, Under the Spell of Gauge Principi (World Scientific, Singapur, 1994), Introducción en línea Archivado el 19 de marzo de 2005 en Wayback Máquina
9. Martinus Veltman, Diagrammatica: El camino hacia los diagramas de Feynman , Cambridge Lecture Notes in Physics, ISBN 0-521-45692-4 
10. Björken, JD; Drell, SD (1965). Campos cuánticos relativistas . Nueva York: McGraw-Hill. pag. viii. ISBN 978-0-07-005494-3.
11. Jorge Cham , Interacción Académica – Diagramas de Feynman, 11 de enero de 2012.
12. Jepsen, Kathryn (5 de agosto de 2014). "Salvando la furgoneta Feynman". Revista Simetría . Consultado el 23 de junio de 2022 .
13. Dubner, Stephen J. (7 de febrero de 2024). "El brillante señor Feynman". Freakonomics . Consultado el 9 de febrero de 2024 .

Fuentes

• 't Hooft, Gerardus; Veltman, Martinus (1973). "Diagrama". Informe amarillo del CERN. doi :10.5170/CERN-1973-009. {{cite journal}}: Citar diario requiere |journal=( ayuda )
• Káiser, David (2005). Separando teorías: la dispersión de los diagramas de Feynman en la física de posguerra . Chicago, IL: Prensa de la Universidad de Chicago. ISBN 0-226-42266-6.
• Veltman, Martinus (16 de junio de 1994). Diagrammatica: El camino hacia los diagramas de Feynman . Notas de conferencias de física de Cambridge. ISBN 0-521-45692-4.(versión ampliada y actualizada de 't Hooft & Veltman, 1973, citado anteriormente)
• Srednicki, Mark (2006). Teoría cuántica de campos. Guion.
• Schweber, SS (1994). QED y los hombres que lo crearon: Dyson, Feynman, Schwinger y Tomonaga . Prensa de la Universidad de Princeton. ISBN 978-0691033273.

enlaces externos

• Artículo de AMS: "Novedades en matemáticas: diagramas de Feynman de dimensión finita"
• Dibuje diagramas de Feynman explicados por Flip Tanedo en Quantumdiaries.com
• Dibujar diagramas de Feynman con la biblioteca FeynDiagram C++ que produce resultados PostScript.
• Herramienta de diagramas en línea Una aplicación gráfica para crear diagramas listos para publicar.
• JaxoDraw Un programa Java para dibujar diagramas de Feynman.
• Bowley, Roger; Copeland, Ed (2010). "Diagramas de Feynman". Sesenta símbolos . Brady Haran para la Universidad de Nottingham .