Diámetro angular

¿Qué tan grande parece una esfera o un círculo?

Diámetro angular: el ángulo subtendido por un objeto.

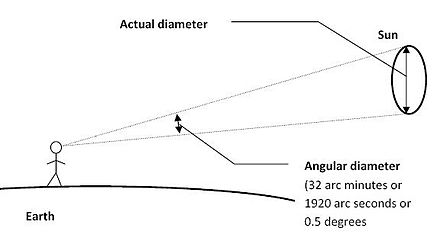
El diámetro angular , tamaño angular , diámetro aparente o tamaño aparente es una distancia angular que describe cuán grande parece una esfera o un círculo desde un punto de vista determinado. En las ciencias de la visión , se denomina ángulo visual y, en óptica , es la apertura angular (de una lente ). El diámetro angular también se puede considerar como el desplazamiento angular a través del cual un ojo o una cámara deben rotar para mirar desde un lado de un círculo aparente al lado opuesto. Los humanos pueden resolver con sus ojos desnudos diámetros de hasta aproximadamente 1  minuto de arco (aproximadamente 0,017° o 0,0003 radianes). ^[1] Esto corresponde a 0,3 m a una distancia de 1 km, o a percibir Venus como un disco en condiciones óptimas.

Fórmula

Diagrama para la fórmula del diámetro angular

El diámetro angular de un círculo cuyo plano es perpendicular al vector de desplazamiento entre el punto de vista y el centro de dicho círculo se puede calcular mediante la fórmula ^{[2] [3]}

${\displaystyle \delta =2\arctan \left({\frac {d}{2D}}\right),}$

donde es el diámetro angular en grados , y es el diámetro real del objeto, y es la distancia al objeto. Cuando , tenemos , ^[4] y el resultado obtenido está en radianes . ${\displaystyle \delta }$ ${\displaystyle d}$ ${\displaystyle D}$ ${\displaystyle D\gg d}$ ${\displaystyle \delta \approx d/D}$

Para un objeto esférico cuyo diámetro real es igual a y donde es la distancia al centro de la esfera, el diámetro angular se puede encontrar mediante la siguiente fórmula modificada ^{[ cita requerida ]} ${\displaystyle d_{\mathrm {act} },}$ ${\displaystyle D}$

${\displaystyle \delta =2\arcsin \left({\frac {d_{\mathrm {act} }}{2D}}\right)}$

La diferencia se debe a que los bordes aparentes de una esfera son sus puntos tangentes, que están más cerca del observador que el centro de la esfera y tienen una distancia entre ellos que es menor que el diámetro real. La fórmula anterior se puede encontrar entendiendo que en el caso de un objeto esférico, se puede construir un triángulo rectángulo de modo que sus tres vértices sean el observador, el centro de la esfera y uno de los puntos tangentes de la esfera, con como hipotenusa y como seno. ^{[ cita requerida ]} ${\displaystyle D}$ ${\displaystyle {\frac {d_{\mathrm {act} }}{2D}}}$

La diferencia es significativa sólo para objetos esféricos de gran diámetro angular, ya que las siguientes aproximaciones de ángulos pequeños son válidas para valores pequeños de : ^[5] ${\displaystyle x}$

${\displaystyle \arcsin x\approx \arctan x\approx x.}$

Estimación del diámetro angular usando la mano

Ángulos aproximados de 10°, 20°, 5° y 1° para la mano extendida con el brazo extendido.

Se pueden obtener estimaciones del diámetro angular sosteniendo la mano en ángulo recto con el brazo completamente extendido , como se muestra en la figura. ^{[6] [7] [8]}

Uso en astronomía

Una representación del siglo XIX del tamaño aparente del Sol visto desde los planetas del Sistema Solar (incluidos 72 Feronia y el asteroide más alejado conocido en ese momento, llamado aquí Maximiliana ).

En astronomía , los tamaños de los objetos celestes se dan a menudo en términos de su diámetro angular visto desde la Tierra , en lugar de sus tamaños reales. Dado que estos diámetros angulares son típicamente pequeños, es común presentarlos en segundos de arco (″). Un segundo de arco es 1/3600 de un grado (1°) y un radián es 180/ π grados. Por lo tanto, un radián equivale a 3600 × 180/ segundos de arco, que son aproximadamente 206 265 segundos de arco (1 rad ≈ 206 264,806247"). Por lo tanto, el diámetro angular de un objeto con diámetro físico d a una distancia D , expresado en segundos de arco, viene dado por: ^[9] ${\displaystyle \pi }$

${\displaystyle \delta =206,265~(d/D)~\mathrm {arcseconds} }$.

Estos objetos tienen un diámetro angular de 1″:

• un objeto de 1 cm de diámetro a una distancia de 2,06 km
• un objeto de diámetro 725,27 km a una distancia de 1 unidad astronómica (UA)
• un objeto de diámetro 45 866 916 km a 1 año luz
• un objeto de diámetro 1 UA (149 597 871 km) a una distancia de 1 parsec (pc)

Por lo tanto, el diámetro angular de la órbita de la Tierra alrededor del Sol visto desde una distancia de 1 pc es 2″, ya que 1 UA es el radio medio de la órbita de la Tierra.

El diámetro angular del Sol, desde una distancia de un año luz , es de 0,03″, y el de la Tierra, de 0,0003″. El diámetro angular de 0,03″ del Sol indicado anteriormente es aproximadamente el mismo que el de un cuerpo humano a una distancia del diámetro de la Tierra.

Esta tabla muestra los tamaños angulares de cuerpos celestes notables vistos desde la Tierra:

Diagrama logarítmico del diámetro de apertura frente a la resolución angular en el límite de difracción para varias longitudes de onda de luz en comparación con varios instrumentos astronómicos. Por ejemplo, la estrella azul muestra que el telescopio espacial Hubble está casi limitado por la difracción en el espectro visible a 0,1 segundos de arco, mientras que el círculo rojo muestra que el ojo humano debería tener un poder de resolución de 20 segundos de arco en teoría, aunque normalmente solo 60 segundos de arco.

Comparación del diámetro angular del Sol, la Luna y los planetas. Para obtener una representación real de los tamaños, observe la imagen a una distancia de 103 veces el ancho del círculo "Luna: máx." Por ejemplo, si este círculo tiene 5 cm de ancho en su monitor, mírelo a 5,15 m de distancia.

Esta foto compara los tamaños aparentes de Júpiter y sus cuatro lunas galileanas ( Calisto en máxima elongación ) con el diámetro aparente de la Luna llena durante su conjunción el 10 de abril de 2017.

El diámetro angular del Sol, visto desde la Tierra, es aproximadamente 250.000 veces el de Sirio . (Sirio tiene el doble de diámetro y su distancia es 500.000 veces mayor; el Sol es 10 ¹⁰ veces más brillante, lo que corresponde a una relación de diámetro angular de 10 ⁵ , por lo que Sirio es aproximadamente 6 veces más brillante por unidad de ángulo sólido .)

El diámetro angular del Sol también es aproximadamente 250.000 veces el de Alfa Centauri A (tiene aproximadamente el mismo diámetro y la distancia es 250.000 veces mayor; el Sol es 4×10 ¹⁰ veces más brillante, lo que corresponde a una relación de diámetro angular de 200.000, por lo que Alfa Centauri A es un poco más brillante por unidad de ángulo sólido).

El diámetro angular del Sol es aproximadamente el mismo que el de la Luna . (El diámetro del Sol es 400 veces mayor y su distancia también; el Sol es entre 200.000 y 500.000 veces más brillante que la Luna llena (las cifras varían), lo que corresponde a una relación de diámetro angular de 450 a 700, por lo que un cuerpo celeste con un diámetro de 2,5–4″ y el mismo brillo por unidad de ángulo sólido tendría el mismo brillo que la Luna llena).

Aunque Plutón es físicamente más grande que Ceres, cuando se lo observa desde la Tierra (por ejemplo, a través del telescopio espacial Hubble ) Ceres tiene un tamaño aparente mucho mayor.

Los tamaños angulares medidos en grados son útiles para áreas más grandes del cielo. (Por ejemplo, las tres estrellas del Cinturón cubren aproximadamente 4,5° de tamaño angular). Sin embargo, se necesitan unidades mucho más precisas para medir los tamaños angulares de galaxias, nebulosas u otros objetos del cielo nocturno .

Los grados, por tanto, se subdividen de la siguiente manera:

• 360 grados (°) en un círculo completo
• 60 minutos de arco ( ′ ) en un grado
• 60 segundos de arco (″) en un minuto de arco

Para poner esto en perspectiva, la Luna llena vista desde la Tierra tiene un ángulo de aproximadamente 1 ⁄ 2 °, o 30 ′ (o 1800″). El movimiento de la Luna a través del cielo se puede medir en tamaño angular: aproximadamente 15° cada hora, o 15″ por segundo. Una línea de una milla de largo pintada en la cara de la Luna parecería desde la Tierra tener aproximadamente 1″ de longitud.

Distancias mínima, media y máxima de la Luna a la Tierra con su diámetro angular visto desde la superficie de la Tierra, a escala

En astronomía, suele ser difícil medir directamente la distancia a un objeto, aunque el objeto puede tener un tamaño físico conocido (quizás es similar a un objeto más cercano con una distancia conocida) y un diámetro angular medible. En ese caso, la fórmula del diámetro angular se puede invertir para obtener la distancia del diámetro angular a objetos distantes como

${\displaystyle d\equiv 2D\tan \left({\frac {\delta }{2}}\right).}$

En el espacio no euclidiano, como nuestro universo en expansión, la distancia del diámetro angular es solo una de varias definiciones de distancia, de modo que puede haber diferentes "distancias" al mismo objeto. Véase Medidas de distancia (cosmología) .

Objetos no circulares

Muchos objetos del cielo profundo, como las galaxias y las nebulosas, parecen no circulares y, por lo tanto, se les asignan dos medidas de diámetro: eje mayor y eje menor. Por ejemplo, la Pequeña Nube de Magallanes tiene un diámetro visual aparente de 5° 20′ × 3° 5′.

Defecto de iluminación

El defecto de iluminación es el ancho angular máximo de la parte no iluminada de un cuerpo celeste que ve un observador determinado. Por ejemplo, si un objeto tiene un arco de 40″ de ancho y está iluminado en un 75 %, el defecto de iluminación es de 10″.

Véase también

• Distancia de diámetro angular
• Resolución angular
• Angulo solido
• Agudeza visual
• Angulo visual
• Ángulo visual percibido
• Lista de estrellas con imágenes resueltas
• Magnitud aparente

Referencias

1. Yanoff, Myron; Duker, Jay S. (2009). Oftalmología, 3.ª edición. MOSBY Elsevier. pág. 54. ISBN 978-0444511416.
2. Esto se puede obtener utilizando la fórmula para la longitud de una cuerda que se encuentra en "Segmento circular". Archivado desde el original el 21 de diciembre de 2014. Consultado el 23 de enero de 2015 .
3. "Diámetro angular | Repositorio de fórmulas de Wolfram". resources.wolframcloud.com . Consultado el 10 de abril de 2024 .
4. "Notas 7A: Tamaño angular/Distancia y áreas" (PDF) .
5. "Una serie de Taylor para el funcionarco" (PDF) . Archivado desde el original (PDF) el 2015-02-18 . Consultado el 2015-01-23 .
6. "Sistemas de coordenadas". Archivado desde el original el 21 de enero de 2015. Consultado el 21 de enero de 2015 .
7. "Fotografiando satélites". 8 de junio de 2013. Archivado desde el original el 21 de enero de 2015.
8. Wikiversidad: Laboratorios de Física y Astronomía/Tamaño angular
9. Michael A. Seeds; Dana E. Backman (2010). Estrellas y galaxias (7.ª ed.). Brooks Cole. pág. 39. ISBN 978-0-538-73317-5.
10. O'Meara, Stephen James (6 de agosto de 2019). "Los sacos de carbón de Cygnus". Astronomy.com . Consultado el 10 de febrero de 2023 .
11. Dobashi, Kazuhito; Matsumoto, Tomoaki; Shimoikura, Tomomi; Saito, Hiro; Akisato, Ko; Ohashi, Kenjiro; Nakagomi, Keisuke (24 de noviembre de 2014). "Filamentos en colisión y un núcleo denso masivo en la nube molecular Cygnus Ob 7". La revista astrofísica . 797 (1). Sociedad Astronómica Estadounidense: 58. arXiv : 1411.0942 . Código Bib : 2014ApJ...797...58D. doi :10.1088/0004-637x/797/1/58. ISSN  1538-4357. S2CID  118369651.
12. Gorkavyi, Nick; Krotkov, Nickolay; Marshak, Alexander (24 de marzo de 2023). "Observaciones de la Tierra desde la superficie de la Luna: dependencia de la libración lunar". Técnicas de medición atmosférica . 16 (6). Copernicus GmbH: 1527–1537. Bibcode :2023AMT....16.1527G. doi : 10.5194/amt-16-1527-2023 . ISSN  1867-8548.
13. "El Sol y los tránsitos vistos desde los planetas". RASC Calgary Centre . 2018-11-05 . Consultado el 2024-08-23 .
14. "¿Qué tan grande se ve el Sol desde Mercurio y Venus, en comparación con cómo lo vemos desde la Tierra?". Revista Astronomy . 2018-05-31 . Consultado el 2024-08-23 .
15. "Problema 346: La Estación Espacial Internacional y una mancha solar: exploración de escalas angulares" (PDF) . Matemáticas espaciales @ NASA ! . 2018-08-19 . Consultado el 2022-05-20 .
16. Wong, Yan (24 de enero de 2016). "¿Qué tan pequeño puede ver el ojo desnudo?". BBC Science Focus Magazine . Consultado el 23 de mayo de 2022 .
17. "Ojos agudos: ¿qué tan bien podemos ver realmente?". Science in School – scienceinschool.org . 2016-09-07 . Consultado el 2022-05-23 .
18. Graney, Christopher M. (10 de diciembre de 2006). "La precisión de las observaciones de Galileo y la búsqueda temprana de paralaje estelar". arXiv : physics/0612086 . doi :10.1007/3-540-50906-2_2. {{cite journal}}: Requiere citar revista |journal=( ayuda )
19. "El telescopio de Galileo: cómo funciona". Esposizioni on-line - Istituto e Museo di Storia della Scienza (en italiano) . Consultado el 21 de mayo de 2022 .
20. Anugu, Narsireddy; Baron, Fabien; Monnier, John D.; Gies, Douglas R.; Roettenbacher, Rachael M.; Schaefer, Gail H.; Montargès, Miguel; Kraus, Stefan; Bouquin, Jean-Baptiste Le (5 de agosto de 2024). "Imágenes de infrarrojo cercano de CHARA de la estrella hipergigante amarilla $\rho$ Cassiopeiae: células de convección y envoltura circunestelar". arXiv.org . Consultado el 12 de agosto de 2024 .
21. Su diámetro angular es 800 000 veces menor que el de Alnitak visto desde la Tierra. Alnitak es una estrella azul, por lo que emite mucha luz para su tamaño. Si estuviera 800 000 veces más lejos, su magnitud sería 31,5, el límite de lo que el Hubble puede ver.

Enlaces externos

• Fórmula de ángulo pequeño (archivada el 7 de octubre de 1997)
• Ayuda visual para el tamaño aparente de los planetas