Una secuencia de longitud máxima ( MLS ) es un tipo de secuencia binaria pseudoaleatoria .
Son secuencias de bits generadas utilizando registros de desplazamiento de retroalimentación lineal máxima y se denominan así porque son periódicas y reproducen todas las secuencias binarias (excepto el vector cero) que pueden representarse mediante los registros de desplazamiento (es decir, para registros de longitud m producen una secuencia de longitud 2 m − 1). A un MLS también se lo denomina a veces secuencia n o secuencia m . Los MLS son espectralmente planos , con la excepción de un término de CC cercano a cero.
Estas secuencias pueden representarse como coeficientes de polinomios irreducibles en un anillo polinomial sobre Z/2Z .
Las aplicaciones prácticas de los MLS incluyen la medición de respuestas de impulsos (por ejemplo, de la reverberación de una sala o de los tiempos de llegada de fuentes remolcadas en el océano [1] ). También se utilizan como base para derivar secuencias pseudoaleatorias en sistemas de comunicación digital que emplean sistemas de transmisión de espectro ensanchado por salto de frecuencia y de espectro ensanchado por secuencia directa , y en el diseño eficiente de algunos experimentos de fMRI . [2]
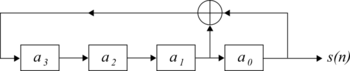
Los MLS se generan utilizando registros de desplazamiento de retroalimentación lineal máxima . En la figura 1 se muestra un sistema generador de MLS con un registro de desplazamiento de longitud 4. Se puede expresar utilizando la siguiente relación recursiva:
donde n es el índice de tiempo y representa la suma en módulo 2. Para los valores de bit 0 = FALSO o 1 = VERDADERO, esto es equivalente a la operación XOR.
Como los MLS son periódicos y los registros de desplazamiento recorren todos los valores binarios posibles (con la excepción del vector cero), los registros se pueden inicializar en cualquier estado, con la excepción del vector cero.
Un polinomio sobre GF(2) se puede asociar con el registro de desplazamiento de retroalimentación lineal. Tiene un grado de la longitud del registro de desplazamiento y coeficientes que son 0 o 1, correspondientes a las tomas del registro que alimentan la compuerta xor . Por ejemplo, el polinomio correspondiente a la Figura 1 es .
Una condición necesaria y suficiente para que la secuencia generada por un LFSR tenga longitud máxima es que su polinomio correspondiente sea primitivo . [3]
Los MLS son económicos de implementar en hardware o software, y los registros de desplazamiento de retroalimentación de orden relativamente bajo pueden generar secuencias largas; una secuencia generada usando un registro de desplazamiento de longitud 20 tiene una longitud de 2 · 20 − 1 muestras (1.048.575 muestras).
Los MLS tienen las siguientes propiedades, según lo formulado por Solomon Golomb . [4]
La ocurrencia de 0 y 1 en la secuencia debe ser aproximadamente la misma. Más precisamente, en una secuencia de longitud máxima hay unos y ceros. La cantidad de unos es igual a la cantidad de ceros más uno, ya que no puede ocurrir el estado que contiene solo ceros.
Una "secuencia" es una subsecuencia de "1" consecutivos o "0" consecutivos dentro del MLS en cuestión. El número de secuencias es el número de dichas subsecuencias. [ vago ]
De todas las "ejecuciones" (que consisten en "1" o "0") en la secuencia:
La autocorrelación circular de un MLS es una función delta de Kronecker [5] [6] (con desplazamiento de CC y retardo de tiempo, según la implementación). Para la convención ±1, es decir, se asigna el valor de bit 1 y el valor de bit 0 , asignando XOR al negativo del producto:
donde representa el conjugado complejo y representa un desplazamiento circular .
La autocorrelación lineal de un MLS se aproxima a un delta de Kronecker.
Si se va a medir la respuesta al impulso de un sistema lineal invariante en el tiempo (LTI) utilizando un MLS, la respuesta se puede extraer de la salida del sistema medida y [ n ] tomando su correlación cruzada circular con el MLS. Esto se debe a que la autocorrelación de un MLS es 1 para un desfase cero y casi cero (−1/ N donde N es la longitud de la secuencia) para todos los demás desfases; en otras palabras, se puede decir que la autocorrelación del MLS se aproxima a la función de impulso unitario a medida que aumenta la longitud del MLS.
Si la respuesta al impulso de un sistema es h [ n ] y la MLS es s [ n ], entonces
Tomando la correlación cruzada con respecto a s [ n ] de ambos lados,
y suponiendo que φ ss es un impulso (válido para secuencias largas)
Cualquier señal con una autocorrelación impulsiva puede usarse para este propósito, pero las señales con un factor de cresta alto , como el impulso mismo, producen respuestas de impulso con una mala relación señal-ruido . Se asume comúnmente que el MLS sería entonces la señal ideal, ya que consta solo de valores de escala completa y su factor de cresta digital es el mínimo, 0 dB. [7] [8] Sin embargo, después de la reconstrucción analógica , las discontinuidades agudas en la señal producen picos fuertes entre muestras, degradando el factor de cresta en 4-8 dB o más, aumentando con la longitud de la señal, haciéndolo peor que un barrido sinusoidal. [9] Se han diseñado otras señales con un factor de cresta mínimo, aunque se desconoce si se puede mejorar más allá de 3 dB. [10]
Cohn y Lempel [11] demostraron la relación entre la MLS y la transformada de Hadamard . Esta relación permite calcular la correlación de una MLS mediante un algoritmo rápido similar a la FFT .
es una secuencia binaria cuya autocorrelación circular (excepto un pequeño error DC) es una función delta.
Sus valores RMS y pico son X, lo que hace que su factor de cresta (pico/RMS) sea igual a 1, el más bajo que puede alcanzar.
El factor de cresta para MLS es muy cercano a 1, por lo que tiene sentido utilizar este tipo de señal de entrada cuando necesitamos una alta relación señal-ruido para nuestra medición.
La secuencia de longitud máxima (MLS) teóricamente cumple con los requisitos porque tiene un factor de cresta matemático de 0 dB, el factor de cresta más bajo posible. Sin embargo, en la práctica, las transiciones abruptas y la reproducción limitada por el ancho de banda de la señal dan como resultado un factor de cresta de aproximadamente 8 dB