
Una compuerta lógica es un dispositivo que realiza una función booleana , una operación lógica realizada en una o más entradas binarias que produce una única salida binaria. Según el contexto, el término puede referirse a una compuerta lógica ideal , una que tiene, por ejemplo, tiempo de subida cero y abanico de salida ilimitado , o puede referirse a un dispositivo físico no ideal [1] (consulte amplificadores operacionales ideales y reales para comparar).
La forma principal de construir puertas lógicas utiliza diodos o transistores que actúan como interruptores electrónicos . Hoy en día, la mayoría de las puertas lógicas están hechas de MOSFET ( transistores de efecto de campo de metal-óxido-semiconductor ). [2] También se pueden construir utilizando tubos de vacío , relés electromagnéticos con lógica de relé , lógica fluídica , lógica neumática , óptica , moléculas , acústica [3] o incluso elementos mecánicos o térmicos [4] .
Las puertas lógicas se pueden conectar en cascada de la misma manera que se pueden componer funciones booleanas, lo que permite la construcción de un modelo físico de toda la lógica booleana y, por lo tanto, de todos los algoritmos y matemáticas que se pueden describir con la lógica booleana. Los circuitos lógicos incluyen dispositivos como multiplexores , registros , unidades aritmético lógicas (ALU) y memoria de computadora , hasta llegar a microprocesadores completos , [5] que pueden contener más de 100 millones de puertas lógicas.
Las puertas lógicas compuestas AND-OR-Invert (AOI) y OR-AND-Invert (OAI) se emplean a menudo en el diseño de circuitos porque su construcción utilizando MOSFET es más simple y más eficiente que la suma de las puertas individuales. [6]
El sistema numérico binario fue refinado por Gottfried Wilhelm Leibniz (publicado en 1705), influenciado por el sistema binario del antiguo I Ching . [7] [8] Leibniz estableció que el uso del sistema binario combinaba los principios de la aritmética y la lógica .
En una carta de 1886, Charles Sanders Peirce describió cómo se podían llevar a cabo operaciones lógicas mediante circuitos de conmutación eléctricos. [9] Las primeras computadoras electromecánicas se construyeron a partir de interruptores y lógica de relés en lugar de las innovaciones posteriores de tubos de vacío (válvulas termoiónicas) o transistores (a partir de los cuales se construyeron computadoras electrónicas posteriores). Ludwig Wittgenstein introdujo una versión de la tabla de verdad de 16 filas como proposición 5.101 del Tractatus Logico-Philosophicus (1921). Walther Bothe , inventor del circuito de coincidencia , [10] obtuvo parte del Premio Nobel de Física de 1954, por la primera puerta AND electrónica moderna en 1924. Konrad Zuse diseñó y construyó puertas lógicas electromecánicas para su computadora Z1 (de 1935 a 1938).
De 1934 a 1936, el ingeniero de NEC Akira Nakashima , Claude Shannon y Victor Shestakov introdujeron la teoría de circuitos de conmutación en una serie de artículos que mostraban que el álgebra booleana de dos valores , que descubrieron de forma independiente, puede describir el funcionamiento de los circuitos de conmutación. [11] [12] [13] [14] El uso de esta propiedad de los interruptores eléctricos para implementar la lógica es el concepto fundamental que subyace a todas las computadoras digitales electrónicas . La teoría de circuitos de conmutación se convirtió en la base del diseño de circuitos digitales , ya que se hizo ampliamente conocida en la comunidad de ingeniería eléctrica durante y después de la Segunda Guerra Mundial , y el rigor teórico reemplazó a los métodos ad hoc que habían prevalecido anteriormente. [14]
En 1948, Bardeen y Brattain patentaron un transistor de puerta aislada (IGFET) con una capa de inversión. Su concepto constituye la base de la tecnología CMOS actual. [15] En 1957, Frosch y Derick pudieron fabricar puertas planas PMOS y NMOS . [16] Más tarde, un equipo de Bell Labs demostró un MOS funcional con puertas PMOS y NMOS . [17] Ambos tipos fueron combinados y adaptados posteriormente en lógica MOS complementaria (CMOS) por Chih-Tang Sah y Frank Wanlass en Fairchild Semiconductor en 1963. [18]
Existen dos conjuntos de símbolos para puertas lógicas elementales de uso común, ambos definidos en la norma ANSI / IEEE Std 91-1984 y su suplemento ANSI/IEEE Std 91a-1991. El conjunto de "forma distintiva", basado en esquemas tradicionales, se utiliza para dibujos simples y deriva del estándar militar estadounidense MIL-STD-806 de los años 1950 y 1960. [19] A veces se lo describe extraoficialmente como "militar", lo que refleja su origen. El conjunto de "forma rectangular", basado en ANSI Y32.14 y otros estándares industriales tempranos que luego fueron refinados por IEEE e IEC, tiene contornos rectangulares para todos los tipos de puertas y permite la representación de una gama mucho más amplia de dispositivos de lo que es posible con los símbolos tradicionales. [20] La norma IEC, IEC 60617-12, ha sido adoptada por otras normas, como EN 60617-12:1999 en Europa, BS EN 60617-12:1999 en el Reino Unido y DIN EN 60617-12:1998 en Alemania.
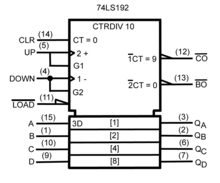
El objetivo común de la norma IEEE Std 91-1984 y la IEC 617-12 era proporcionar un método uniforme para describir las funciones lógicas complejas de los circuitos digitales con símbolos esquemáticos. Estas funciones eran más complejas que las simples puertas AND y OR. Podían ser circuitos de escala media, como un contador de 4 bits, o circuitos de gran escala, como un microprocesador.
La norma IEC 617-12 y su sucesora renumerada IEC 60617-12 no muestran explícitamente los símbolos de "forma distintiva", pero no los prohíben. [20] Sin embargo, estos se muestran en la norma ANSI/IEEE Std 91 (y 91a) con esta nota: "El símbolo de forma distintiva, según la publicación IEC 617, parte 12, no es el preferido, pero no se considera que esté en contradicción con esa norma". La norma IEC 60617-12 contiene la nota correspondiente (sección 2.1) "Aunque no sea el preferido, el uso de otros símbolos reconocidos por las normas nacionales oficiales, es decir, formas distintivas en lugar de símbolos [lista de puertas básicas], no se considerará en contradicción con esta norma. Se desaconseja el uso de estos otros símbolos en combinación para formar símbolos complejos (por ejemplo, el uso como símbolos integrados)". Este compromiso se alcanzó entre los respectivos grupos de trabajo IEEE e IEC para permitir que las normas IEEE e IEC cumplieran mutuamente entre sí.
En la década de 1980, los esquemas eran el método predominante para diseñar tanto placas de circuitos como circuitos integrados personalizados, conocidos como matrices de compuertas . En la actualidad, los circuitos integrados personalizados y las matrices de compuertas programables en campo se diseñan normalmente con lenguajes de descripción de hardware (HDL), como Verilog o VHDL .
Según las leyes de De Morgan , una función AND es idéntica a una función OR con entradas y salidas negadas. Asimismo, una función OR es idéntica a una función AND con entradas y salidas negadas. Una compuerta NAND es equivalente a una compuerta OR con entradas negadas, y una compuerta NOR es equivalente a una compuerta AND con entradas negadas.
Esto conduce a un conjunto alternativo de símbolos para puertas básicas que utilizan el símbolo central opuesto ( AND u OR ) pero con las entradas y salidas negadas. El uso de estos símbolos alternativos puede hacer que los diagramas de circuitos lógicos sean mucho más claros y ayudar a mostrar la conexión accidental de una salida alta activa a una entrada baja activa o viceversa. Cualquier conexión que tenga negaciones lógicas en ambos extremos se puede reemplazar por una conexión sin negación y un cambio adecuado de puerta o viceversa. Cualquier conexión que tenga una negación en un extremo y ninguna negación en el otro se puede hacer más fácil de interpretar utilizando en su lugar el símbolo equivalente de De Morgan en cualquiera de los dos extremos. Cuando los indicadores de negación o polaridad en ambos extremos de una conexión coinciden, no hay negación lógica en esa ruta (efectivamente, las burbujas se "cancelan"), lo que hace que sea más fácil seguir los estados lógicos de un símbolo al siguiente. Esto se ve comúnmente en diagramas lógicos reales, por lo tanto, el lector no debe adquirir el hábito de asociar las formas exclusivamente como formas OR o AND, sino también tener en cuenta las burbujas en las entradas y salidas para determinar la función lógica "verdadera" indicada.
Un símbolo De Morgan puede mostrar más claramente el propósito lógico primario de una compuerta y la polaridad de sus nodos que se consideran en el estado "señalado" (activo, encendido). Considere el caso simplificado donde se utiliza una compuerta NAND de dos entradas para accionar un motor cuando cualquiera de sus entradas se baja mediante un interruptor. El estado "señalado" (motor encendido) ocurre cuando uno o el otro interruptor está encendido. A diferencia de un símbolo NAND regular, que sugiere lógica AND, la versión De Morgan, una compuerta OR de dos entradas negativas, muestra correctamente que OR es de interés. El símbolo NAND regular tiene una burbuja en la salida y ninguna en las entradas (lo opuesto a los estados que encenderán el motor), pero el símbolo De Morgan muestra tanto las entradas como la salida en la polaridad que impulsará el motor.
El teorema de De Morgan se utiliza más comúnmente para implementar puertas lógicas como combinaciones de solo puertas NAND, o como combinaciones de solo puertas NOR, por razones económicas.
Comparación de salida de varias puertas lógicas:
Charles Sanders Peirce (durante 1880-1881) demostró que las puertas NOR solas (o alternativamente las puertas NAND solas ) pueden usarse para reproducir las funciones de todas las demás puertas lógicas, pero su trabajo al respecto no se publicó hasta 1933. [21] La primera prueba publicada fue realizada por Henry M. Sheffer en 1913, por lo que la operación lógica NAND a veces se denomina trazo de Sheffer ; la NOR lógica a veces se denomina flecha de Peirce . [22] En consecuencia, estas puertas a veces se denominan puertas lógicas universales . [23]
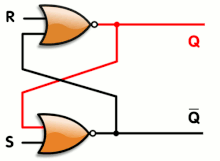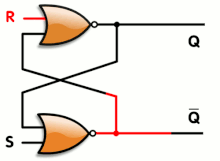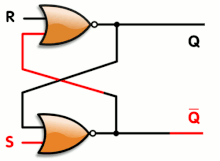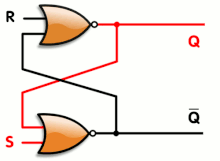
Las puertas lógicas también se pueden utilizar para mantener un estado, lo que permite el almacenamiento de datos. Se puede construir un elemento de almacenamiento conectando varias puertas en un circuito de " enganche ". Los circuitos de enganche se utilizan en la memoria de acceso aleatorio estática . Los diseños más complicados que utilizan señales de reloj y que cambian solo en un flanco ascendente o descendente del reloj se denominan " flip-flops " activados por flanco. Formalmente, un flip-flop se denomina circuito biestable , porque tiene dos estados estables que puede mantener indefinidamente. La combinación de múltiples flip-flops en paralelo, para almacenar un valor de varios bits, se conoce como registro. Cuando se utiliza cualquiera de estas configuraciones de puertas, el sistema general tiene memoria; entonces se denomina sistema lógico secuencial , ya que su salida puede verse influenciada por su(s) estado(s) anterior(es), es decir, por la secuencia de estados de entrada. Por el contrario, la salida de la lógica combinacional es puramente una combinación de sus entradas actuales, no afectada por los estados de entrada y salida anteriores.
Estos circuitos lógicos se utilizan en la memoria de las computadoras . Su rendimiento varía según factores como la velocidad , la complejidad y la fiabilidad del almacenamiento, y se utilizan muchos tipos de diseños diferentes según la aplicación.
Un sistema lógico funcionalmente completo puede estar compuesto de relés , válvulas (tubos de vacío) o transistores .
Las puertas lógicas electrónicas difieren significativamente de sus equivalentes de relé e interruptor. Son mucho más rápidas, consumen mucha menos energía y son mucho más pequeñas (todo por un factor de un millón o más en la mayoría de los casos). Además, existe una diferencia estructural fundamental. El circuito de conmutación crea una ruta metálica continua para que fluya la corriente (en cualquier dirección) entre su entrada y su salida. La puerta lógica semiconductora, por otro lado, actúa como un amplificador de voltaje de alta ganancia , que absorbe una corriente diminuta en su entrada y produce un voltaje de baja impedancia en su salida. No es posible que fluya corriente entre la salida y la entrada de una puerta lógica semiconductora.

Para la lógica a pequeña escala, los diseñadores ahora utilizan puertas lógicas prefabricadas de familias de dispositivos como la serie TTL 7400 de Texas Instruments , la serie CMOS 4000 de RCA y sus descendientes más recientes. Cada vez más, estas puertas lógicas de función fija están siendo reemplazadas por dispositivos lógicos programables , que permiten a los diseñadores empaquetar muchas puertas lógicas mixtas en un solo circuito integrado. La naturaleza programable en campo de los dispositivos lógicos programables como los FPGA ha reducido la propiedad "dura" del hardware; ahora es posible cambiar el diseño lógico de un sistema de hardware reprogramando algunos de sus componentes, lo que permite cambiar las características o la función de una implementación de hardware de un sistema lógico.
Una ventaja importante de las familias de circuitos integrados estandarizados, como las familias 7400 y 4000, es que pueden conectarse en cascada. Esto significa que la salida de una compuerta puede conectarse a las entradas de una o varias otras compuertas, y así sucesivamente. Se pueden construir sistemas con distintos grados de complejidad sin que el diseñador se preocupe demasiado por el funcionamiento interno de las compuertas, siempre que se consideren las limitaciones de cada circuito integrado.
La salida de una compuerta solo puede impulsar un número finito de entradas a otras compuertas, un número llamado " límite de abanico de salida ". Además, siempre hay un retraso, llamado " retardo de propagación ", desde un cambio en la entrada de una compuerta hasta el cambio correspondiente en su salida. Cuando las compuertas están en cascada, el retraso de propagación total es aproximadamente la suma de los retrasos individuales, un efecto que puede convertirse en un problema en circuitos síncronos de alta velocidad . Se puede producir un retraso adicional cuando se conectan muchas entradas a una salida, debido a la capacitancia distribuida de todas las entradas y el cableado y la cantidad finita de corriente que cada salida puede proporcionar.
Existen varias familias lógicas con diferentes características (consumo de energía, velocidad, costo, tamaño) como: RDL (lógica resistencia-diodo), RTL (lógica resistencia-transistor), DTL (lógica diodo-transistor), TTL (lógica transistor-transistor) y CMOS. También existen subvariantes, por ejemplo, lógica CMOS estándar vs. tipos avanzados que aún utilizan tecnología CMOS, pero con algunas optimizaciones para evitar la pérdida de velocidad debido a transistores PMOS más lentos.
La familia más simple de puertas lógicas utiliza transistores bipolares y se denomina lógica de resistencia-transistor (RTL). A diferencia de las puertas lógicas de diodos simples (que no tienen un elemento de ganancia), las puertas RTL se pueden conectar en cascada indefinidamente para producir funciones lógicas más complejas. Las puertas RTL se utilizaron en los primeros circuitos integrados . Para lograr una mayor velocidad y una mejor densidad, las resistencias utilizadas en RTL se reemplazaron por diodos, lo que dio como resultado la lógica de diodo-transistor (DTL). Luego, la lógica de transistor-transistor (TTL) suplantó a la DTL.

A medida que los circuitos integrados se volvieron más complejos, los transistores bipolares fueron reemplazados por transistores de efecto de campo ( MOSFET ) más pequeños; consulte PMOS y NMOS . Para reducir aún más el consumo de energía, la mayoría de las implementaciones de chips contemporáneos de sistemas digitales ahora utilizan lógica CMOS . CMOS utiliza dispositivos MOSFET complementarios (tanto de canal n como de canal p) para lograr una alta velocidad con baja disipación de energía.
Otros tipos de puertas lógicas incluyen, entre otros: [24]
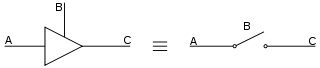
Una puerta lógica de tres estados es un tipo de puerta lógica que puede tener tres salidas diferentes: alta (H), baja (L) y alta impedancia (Z). El estado de alta impedancia no desempeña ningún papel en la lógica, que es estrictamente binaria. Estos dispositivos se utilizan en buses de la CPU para permitir que varios chips envíen datos. Un grupo de tres estados que controlan una línea con un circuito de control adecuado es básicamente equivalente a un multiplexor , que puede estar distribuido físicamente en dispositivos separados o tarjetas enchufables.
En electrónica, una salida alta significaría que la salida está obteniendo corriente del terminal de alimentación positivo (voltaje positivo). Una salida baja significaría que la salida está absorbiendo corriente hacia el terminal de alimentación negativo (voltaje cero). Una impedancia alta significaría que la salida está efectivamente desconectada del circuito.
Las implementaciones no electrónicas son variadas, aunque pocas de ellas se utilizan en aplicaciones prácticas. Muchas de las primeras computadoras digitales electromecánicas, como la Harvard Mark I , se construyeron a partir de puertas lógicas de relé , utilizando relés electromecánicos . Las puertas lógicas se pueden hacer usando dispositivos neumáticos , como el relé de Sorteberg o puertas lógicas mecánicas, incluso a escala molecular. [26] Se han construido varios tipos de puertas lógicas fundamentales utilizando moléculas ( puertas lógicas moleculares ), que se basan en entradas químicas y salidas espectroscópicas. [27] Las puertas lógicas se han hecho a partir de ADN (ver nanotecnología del ADN ) [28] y se han utilizado para crear una computadora llamada MAYA (ver MAYA-II ). Las puertas lógicas se pueden hacer a partir de efectos mecánicos cuánticos , ver puerta lógica cuántica . Las puertas lógicas fotónicas utilizan efectos ópticos no lineales .
En principio, cualquier método que conduzca a una compuerta funcionalmente completa (por ejemplo, una compuerta NOR o NAND) se puede utilizar para crear cualquier tipo de circuito lógico digital. Cabe señalar que no es necesario el uso de lógica de 3 estados para sistemas de bus, y se puede reemplazar por multiplexores digitales, que se pueden construir utilizando únicamente compuertas lógicas simples (como compuertas NAND, compuertas NOR o compuertas AND y OR).
uno de los ordenamientos tradicionales de los hexagramas, el orden xiantian tu realizado por Shao Yong, era, con algunas modificaciones, el mismo orden que se encontraba en la aritmética binaria de Leibniz.
{{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace )(3+207+1 páginas) 10:00 min