El teorema de restricción cristalográfica en su forma básica se basó en la observación de que las simetrías rotacionales de un cristal suelen estar limitadas a 2, 3, 4 y 6 veces. Sin embargo, los cuasicristales pueden ocurrir con otras simetrías de patrones de difracción, como 5 veces; éstos no fueron descubiertos hasta 1982 por Dan Shechtman . [1]
Los cristales se modelan como redes discretas , generadas por una lista de traslaciones finitas independientes (Coxeter 1989). Debido a que la discreción requiere que los espacios entre puntos de la red tengan un límite inferior, el grupo de simetrías rotacionales de la red en cualquier punto debe ser un grupo finito (alternativamente, el punto es el único sistema que permite una simetría rotacional infinita). La fuerza del teorema es que no todos los grupos finitos son compatibles con una red discreta; en cualquier dimensión, tendremos sólo un número finito de grupos compatibles.
Los casos especiales de 2D ( grupos de papel tapiz ) y 3D ( grupos espaciales ) son los más utilizados en las aplicaciones y se pueden tratar juntos.
Una simetría de rotación en dimensión 2 o 3 debe mover un punto de red a una sucesión de otros puntos de red en el mismo plano, generando un polígono regular de puntos de red coplanares. Limitemos ahora nuestra atención al plano en el que actúa la simetría (Scherrer 1946), ilustrado con vectores reticulares en la figura.
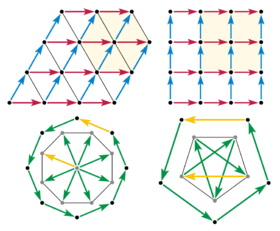
Ahora considere una rotación de 8 veces y los vectores de desplazamiento entre puntos adyacentes del polígono. Si existe un desplazamiento entre dos puntos cualesquiera de la red, entonces ese mismo desplazamiento se repite en todas partes de la red. Así que recopile todos los desplazamientos de los bordes para comenzar en un único punto de la red. Los vectores de arista se convierten en vectores radiales y su simetría de 8 veces implica un octágono regular de puntos de red alrededor del punto de colección. Pero esto es imposible , porque el nuevo octágono es aproximadamente un 80% más grande que el original. La importancia de la contracción es que es ilimitada. La misma construcción se puede repetir con el nuevo octágono, y una y otra vez hasta que la distancia entre los puntos de la red sea tan pequeña como queramos; por tanto, ninguna red discreta puede tener una simetría de 8 veces. El mismo argumento se aplica a cualquier rotación k veces mayor que 6.
Un argumento cada vez más reducido también elimina la simetría quíntuple. Considere un pentágono regular de puntos de red. Si existe, entonces podemos tomar cada dos desplazamientos de borde y (de cabeza a cola) ensamblar una estrella de 5 puntas, con el último borde regresando al punto inicial. Los vértices de una estrella así son nuevamente los vértices de un pentágono regular con simetría quíntuple, pero aproximadamente un 60% más pequeño que el original.
Entonces el teorema esta probado.
La existencia de cuasicristales y teselaciones de Penrose muestra que es necesaria la suposición de una traslación lineal. Los mosaicos de Penrose pueden tener simetría rotacional de 5 veces y una red discreta, y cualquier vecindad local del mosaico se repite infinitas veces, pero no hay una traslación lineal para el mosaico en su conjunto. Y sin el supuesto de red discreta, la construcción anterior no sólo no logra alcanzar una contradicción, sino que produce un contraejemplo (no discreto). Por lo tanto, la simetría rotacional quíntuple no puede eliminarse mediante un argumento que carezca de cualquiera de esos supuestos. Sin embargo, un mosaico de Penrose de todo el plano (infinito) solo puede tener una simetría rotacional exacta de 5 veces (de todo el mosaico) alrededor de un solo punto, mientras que las redes de 4 y 6 veces tienen infinitos centros de simetría rotacional.
Considere dos puntos de la red A y B separados por un vector de traslación r . Considere un ángulo α tal que una rotación del ángulo α alrededor de cualquier punto de la red es una simetría de la red. Girar alrededor del punto B por α asigna el punto A a un nuevo punto A'. De manera similar, rotar alrededor del punto A por α asigna B a un punto B'. Dado que ambas rotaciones mencionadas son operaciones de simetría, A' y B' deben ser puntos de red. Debido a la periodicidad del cristal, el nuevo vector r' que los conecta debe ser igual a un múltiplo entero de r :
con número entero. Los cuatro vectores de traslación, tres de longitud y uno que conecta A' y B', de longitud , forman un trapecio. Por tanto, la longitud de r' también viene dada por:
Combinando las dos ecuaciones se obtiene:
donde también es un número entero. Teniendo en cuenta que hemos permitido números enteros . Al resolver los posibles valores de se revela que los únicos valores en el rango de 0° a 180° son 0°, 60°, 90°, 120° y 180°. En radianes, las únicas rotaciones permitidas consistentes con la periodicidad de la red están dadas por 2π/ n , donde n = 1, 2, 3, 4, 6. Esto corresponde a 1, 2, 3, 4 y 6 veces. simetría, respectivamente, y por lo tanto excluye la posibilidad de una simetría de 5 veces o más de 6 veces.
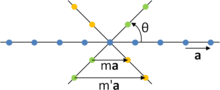
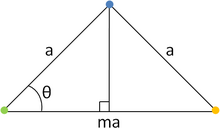
Considere una línea de átomos AOB , separados por una distancia a . Gire toda la fila θ = +2π/ n y θ = −2π/ n , con el punto O mantenido fijo. Después de la rotación de +2π/ n , A se mueve al punto de red C y después de la rotación de -2π/ n , B se mueve al punto de red D. Debido a la supuesta periodicidad de la red, los dos puntos C y D de la red también estarán en una línea directamente debajo de la fila inicial; además, C y D estarán separados por r = ma , siendo m un número entero. Pero por trigonometría, la separación entre estos puntos es:
Al equiparar las dos relaciones se obtiene:
Esto se satisface sólo con n = 1, 2, 3, 4, 6.
Para una prueba alternativa, considere las propiedades de las matrices . La suma de los elementos diagonales de una matriz se llama traza de la matriz. En 2D y 3D, cada rotación es una rotación plana y la traza es función únicamente del ángulo. Para una rotación 2D, la traza es 2 cos θ; para una rotación 3D, 1 + 2 cos θ.
Ejemplos
Al seleccionar una base formada a partir de vectores que abarca la red, no se garantiza ni la ortogonalidad ni la longitud unitaria, solo la independencia lineal. Sin embargo, la traza de la matriz de rotación es la misma con respecto a cualquier base. La traza es una invariante de similitud bajo transformaciones lineales. En la base reticular, la operación de rotación debe mapear cada punto de la red en un número entero de vectores reticulares, por lo que las entradas de la matriz de rotación en la base reticular (y por lo tanto la traza) son necesariamente números enteros. Al igual que en otras pruebas, esto implica que las únicas simetrías rotacionales permitidas corresponden a una invariancia de 1,2,3,4 o 6 veces. Por ejemplo, los papeles pintados y los cristales no se pueden girar 45° y permanecen invariantes, los únicos ángulos posibles son: 360°, 180°, 120°, 90° o 60°.
Ejemplo
La restricción cristalográfica general sobre las rotaciones no garantiza que una rotación sea compatible con una red específica. Por ejemplo, una rotación de 60° no funcionará con una celosía cuadrada; tampoco funcionará una rotación de 90° con una celosía rectangular.
Cuando la dimensión de la red aumenta a cuatro o más, las rotaciones ya no necesitan ser planas; la prueba 2D es inadecuada. Sin embargo, todavía se aplican restricciones, aunque se permiten más simetrías. Por ejemplo, la red hipercúbica tiene una simetría rotacional óctuple, correspondiente a una simetría rotacional óctuple del hipercubo . Esto es de interés, no sólo para las matemáticas, sino también para la física de los cuasicristales según la teoría de cortar y proyectar . En esta visión, un cuasicristal 3D con simetría de rotación de 8 veces podría describirse como la proyección de una losa cortada de una red 4D.
La siguiente matriz de rotación 4D es la simetría óctuple antes mencionada del hipercubo (y el politopo cruzado ):
Transformando esta matriz a las nuevas coordenadas dadas por
Esta tercera matriz corresponde entonces a una rotación tanto de 45° (en las dos primeras dimensiones) como de 135° (en las dos últimas). Proyectar una losa de hipercubos a lo largo de las dos primeras dimensiones de las nuevas coordenadas produce un mosaico de Ammann-Beenker (otro mosaico de este tipo se produce proyectando a lo largo de las dos últimas dimensiones), que por lo tanto también tiene una simetría rotacional de 8 veces en promedio.
La red A4 y la red F4 tienen simetrías rotacionales de orden 10 y orden 12, respectivamente.
Para establecer la restricción para todas las dimensiones, es conveniente desviar la atención de las rotaciones únicamente y concentrarse en las matrices enteras (Bamberg, Cairns y Kilminster 2003). Decimos que una matriz A tiene orden k cuando su k -ésima potencia (pero no inferior), A k , es igual a la identidad. Por tanto, una matriz de rotación séxtuple en la base del triángulo equilátero es una matriz entera de orden 6. Sea Ord N el conjunto de números enteros que pueden ser del orden de una matriz entera N × N. Por ejemplo, Orden 2 = {1, 2, 3, 4, 6}. Deseamos establecer una fórmula explícita para Ord N.
Defina una función ψ basada en la función totiente de Euler φ; asignará números enteros positivos a números enteros no negativos. Para un primo impar , p , y un entero positivo, k , establezca ψ( p k ) igual al valor de la función totiente, φ( p k ), que en este caso es p k − p k−1 . Haga lo mismo para ψ(2 k ) cuando k > 1. Establezca ψ(2) y ψ(1) en 0. Usando el teorema fundamental de la aritmética , podemos escribir cualquier otro entero positivo únicamente como producto de potencias primas, m = Π α p α k α ; establecer ψ( m ) = Σ α ψ( p α k α ). Este se diferencia del paciente en sí, porque es una suma en lugar de un producto.
La restricción cristalográfica en forma general establece que Ord N consta de aquellos enteros positivos m tales que ψ( m ) ≤ N .
Para m >2, los valores de ψ( m ) son iguales al doble del grado algebraico de cos(2π/ m ); por lo tanto, ψ( m ) es estrictamente menor que m y alcanza este valor máximo si y sólo si m es primo .
Estas simetrías adicionales no permiten que un corte plano tenga, digamos, una simetría de rotación de 8 veces. En el avión, todavía se aplican las restricciones 2D. Por tanto, los cortes utilizados para modelar cuasicristales necesariamente tienen espesor.
Las matrices de números enteros no se limitan a rotaciones; por ejemplo, una reflexión también es una simetría de orden 2. Pero al insistir en el determinante +1, podemos restringir las matrices a rotaciones adecuadas .
El teorema de restricción cristalográfica se puede formular en términos de isometrías del espacio euclidiano . Un conjunto de isometrías puede formar un grupo . Por grupo de isometría discreto nos referiremos a un grupo de isometría que asigna cada punto a un subconjunto discreto de R N , es decir, la órbita de cualquier punto es un conjunto de puntos aislados . Con esta terminología, el teorema de restricción cristalográfica en dos y tres dimensiones se puede formular de la siguiente manera.
Las isometrías de orden n incluyen, entre otras, n rotaciones de veces. El teorema también excluye S 8 , S 12 , D 4d y D 6d (ver grupos de puntos en tres dimensiones ), aunque solo tienen simetría rotacional de 4 y 6 veces. La simetría rotacional de cualquier orden alrededor de un eje es compatible con la simetría traslacional a lo largo de ese eje.
El resultado de la tabla anterior implica que para cada grupo de isometría discreto en un espacio de cuatro y cinco dimensiones que incluye traslaciones que abarcan todo el espacio, todas las isometrías de orden finito son de orden 1, 2, 3, 4, 5, 6, 8. , 10 o 12.
Todas las isometrías de orden finito en el espacio de seis y siete dimensiones son de orden 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 24 o 30.