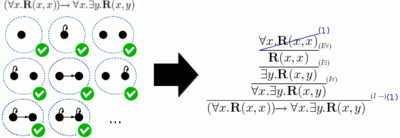
El teorema de completitud de Gödel es un teorema fundamental en lógica matemática que establece una correspondencia entre la verdad semántica y la demostrabilidad sintáctica en la lógica de primer orden .
El teorema de completitud se aplica a cualquier teoría de primer orden : si T es una teoría de este tipo, y φ es una oración (en el mismo lenguaje) y cada modelo de T es un modelo de φ, entonces hay una prueba (de primer orden) de φ usando las afirmaciones de T como axiomas. A veces se dice esto como "todo lo que es verdadero en todos los modelos es demostrable". (Esto no contradice el teorema de incompletitud de Gödel , que trata sobre una fórmula φ u que es indemostrable en una cierta teoría T pero verdadera en el modelo "estándar" de los números naturales: φ u es falsa en algunos otros modelos "no estándar" de T. [1] )
El teorema de completitud establece un vínculo estrecho entre la teoría de modelos , que trata de lo que es verdad en diferentes modelos, y la teoría de la prueba , que estudia lo que se puede demostrar formalmente en sistemas formales particulares .
Fue demostrado por primera vez por Kurt Gödel en 1929. Luego fue simplificado cuando Leon Henkin observó en su tesis doctoral que la parte difícil de la prueba puede presentarse como el Teorema de Existencia Modelo (publicado en 1949). [2] La prueba de Henkin fue simplificada por Gisbert Hasenjaeger en 1953. [3]
Existen numerosos sistemas deductivos para la lógica de primer orden, incluidos los sistemas de deducción natural y los sistemas de estilo Hilbert . Todos los sistemas deductivos tienen en común la noción de deducción formal . Se trata de una secuencia (o, en algunos casos, un árbol finito ) de fórmulas con una conclusión especialmente designada . La definición de deducción es tal que es finita y que es posible verificar algorítmicamente (por medio de una computadora , por ejemplo, o a mano) que una secuencia dada (o árbol) de fórmulas es de hecho una deducción.
Una fórmula de primer orden se denomina lógicamente válida si es verdadera en cada estructura del lenguaje de la fórmula (es decir, para cualquier asignación de valores a las variables de la fórmula). Para enunciar formalmente, y luego demostrar, el teorema de completitud, es necesario también definir un sistema deductivo. Un sistema deductivo se denomina completo si cada fórmula lógicamente válida es la conclusión de alguna deducción formal, y el teorema de completitud para un sistema deductivo particular es el teorema de que es completo en este sentido. Por lo tanto, en cierto sentido, hay un teorema de completitud diferente para cada sistema deductivo. Un inverso de la completitud es la solidez , el hecho de que solo las fórmulas lógicamente válidas son demostrables en el sistema deductivo.
Si algún sistema deductivo específico de lógica de primer orden es sólido y completo, entonces es "perfecto" (una fórmula es demostrable si y sólo si es lógicamente válida), y por lo tanto equivalente a cualquier otro sistema deductivo con la misma calidad (cualquier prueba en un sistema puede convertirse en el otro).
Primero fijamos un sistema deductivo de cálculo de predicados de primer orden, eligiendo cualquiera de los sistemas equivalentes conocidos. La prueba original de Gödel suponía el sistema de pruebas de Hilbert-Ackermann.
El teorema de completitud dice que si una fórmula es lógicamente válida entonces hay una deducción finita (una prueba formal) de la fórmula.
Así, el sistema deductivo es "completo" en el sentido de que no se requieren reglas de inferencia adicionales para probar todas las fórmulas lógicamente válidas. Un inverso de la completitud es la solidez , el hecho de que sólo las fórmulas lógicamente válidas son demostrables en el sistema deductivo. Junto con la solidez (cuya verificación es fácil), este teorema implica que una fórmula es lógicamente válida si y sólo si es la conclusión de una deducción formal.
El teorema puede expresarse de manera más general en términos de consecuencia lógica . Decimos que una oración s es una consecuencia sintáctica de una teoría T , denotada , si s es demostrable a partir de T en nuestro sistema deductivo. Decimos que s es una consecuencia semántica de T , denotada , si s se cumple en cada modelo de T. El teorema de completitud dice entonces que para cualquier teoría de primer orden T con un lenguaje bien ordenable , y cualquier oración s en el lenguaje de T ,
Como el recíproco (la solidez) también es válido, se deduce que si y sólo si , y por tanto que la consecuencia sintáctica y semántica son equivalentes para la lógica de primer orden.
Este teorema más general se utiliza implícitamente, por ejemplo, cuando se demuestra que una oración se puede demostrar a partir de los axiomas de la teoría de grupos considerando un grupo arbitrario y mostrando que la oración es satisfecha por ese grupo.
La formulación original de Gödel se deduce tomando el caso particular de una teoría sin ningún axioma.
El teorema de completitud también puede entenderse en términos de consistencia , como consecuencia del teorema de existencia del modelo de Henkin . Decimos que una teoría T es sintácticamente consistente si no existe ninguna oración s tal que tanto s como su negación ¬ s sean demostrables a partir de T en nuestro sistema deductivo. El teorema de existencia del modelo dice que para cualquier teoría de primer orden T con un lenguaje bien ordenable,
Otra versión, con conexiones con el teorema de Löwenheim-Skolem , dice:
Dado el teorema de Henkin, el teorema de completitud se puede demostrar de la siguiente manera: Si , entonces no tiene modelos. Por el contrapositivo del teorema de Henkin, entonces es sintácticamente inconsistente. Por lo tanto, una contradicción ( ) es demostrable a partir de en el sistema deductivo. Por lo tanto , y luego por las propiedades del sistema deductivo, .
El teorema de existencia del modelo y su demostración pueden formalizarse en el marco de la aritmética de Peano . Precisamente, podemos definir sistemáticamente un modelo de cualquier teoría de primer orden efectiva consistente T en la aritmética de Peano interpretando cada símbolo de T mediante una fórmula aritmética cuyas variables libres son los argumentos del símbolo. (En muchos casos, necesitaremos suponer, como hipótesis de la construcción, que T es consistente, ya que la aritmética de Peano puede no probar ese hecho.) Sin embargo, la definición expresada por esta fórmula no es recursiva (sino que es, en general, Δ 2 ).
Una consecuencia importante del teorema de completitud es que es posible enumerar recursivamente las consecuencias semánticas de cualquier teoría de primer orden efectiva , enumerando todas las posibles deducciones formales de los axiomas de la teoría, y usar esto para producir una enumeración de sus conclusiones.
Esto contrasta con el significado directo de la noción de consecuencia semántica, que cuantifica todas las estructuras de una lengua particular, lo que claramente no es una definición recursiva.
Además, hace que el concepto de "demostrabilidad", y por tanto de "teorema", sea un concepto claro que sólo depende del sistema de axiomas elegido de la teoría, y no de la elección de un sistema de prueba.
Los teoremas de incompletitud de Gödel muestran que existen limitaciones inherentes a lo que se puede demostrar dentro de cualquier teoría dada de primer orden en matemáticas. La "incompletitud" en su nombre se refiere a otro significado de completo (véase teoría de modelos – Uso de los teoremas de compacidad y completitud ): Una teoría es completa (o decidible) si cada oración en el lenguaje de es demostrable ( ) o refutable ( ).
El primer teorema de incompletitud establece que cualquier oración que sea consistente , efectiva y contenga aritmética de Robinson (" Q ") debe ser incompleta en este sentido, al construir explícitamente una oración que no sea demostrable ni refutable dentro de . El segundo teorema de incompletitud extiende este resultado al mostrar que puede elegirse de modo que exprese la consistencia de sí misma.
Como no se puede probar en , el teorema de completitud implica la existencia de un modelo de en el que es falso. De hecho, es una oración Π 1 , es decir, establece que alguna propiedad finitista es verdadera para todos los números naturales; por lo que si es falsa, entonces algún número natural es un contraejemplo. Si este contraejemplo existiera dentro de los números naturales estándar, su existencia refutaría dentro de ; pero el teorema de incompletitud mostró que esto es imposible, por lo que el contraejemplo no debe ser un número estándar y, por lo tanto, cualquier modelo de en el que es falso debe incluir números no estándar .
De hecho, el modelo de cualquier teoría que contenga Q obtenida por la construcción sistemática del teorema de existencia del modelo aritmético, es siempre no estándar con un predicado de demostrabilidad no equivalente y una forma no equivalente de interpretar su propia construcción, de modo que esta construcción es no recursiva (ya que las definiciones recursivas serían inequívocas).
Además, si es al menos ligeramente más fuerte que Q (por ejemplo, si incluye la inducción para fórmulas existenciales acotadas), entonces el teorema de Tennenbaum muestra que no tiene modelos no estándar recursivos.
El teorema de completitud y el teorema de compacidad son dos piedras angulares de la lógica de primer orden. Si bien ninguno de estos teoremas puede demostrarse de manera completamente efectiva , cada uno de ellos puede obtenerse efectivamente a partir del otro.
El teorema de compacidad dice que si una fórmula φ es una consecuencia lógica de un conjunto (posiblemente infinito) de fórmulas Γ, entonces es una consecuencia lógica de un subconjunto finito de Γ. Esta es una consecuencia inmediata del teorema de completitud, porque solo un número finito de axiomas de Γ pueden mencionarse en una deducción formal de φ, y la solidez del sistema deductivo implica entonces que φ es una consecuencia lógica de este conjunto finito. Esta demostración del teorema de compacidad se debe originalmente a Gödel.
Por el contrario, para muchos sistemas deductivos, es posible demostrar el teorema de completitud como una consecuencia efectiva del teorema de compacidad.
La ineficacia del teorema de completitud se puede medir siguiendo los lineamientos de las matemáticas inversas . Cuando se consideran sobre un lenguaje contable, los teoremas de completitud y compacidad son equivalentes entre sí y equivalentes a una forma débil de elección conocida como lema débil de König , con la equivalencia demostrable en RCA 0 (una variante de segundo orden de la aritmética de Peano restringida a la inducción sobre fórmulas Σ 0 1 ). El lema débil de König es demostrable en ZF, el sistema de la teoría de conjuntos de Zermelo-Fraenkel sin axioma de elección, y por lo tanto los teoremas de completitud y compacidad para lenguajes contables son demostrables en ZF. Sin embargo, la situación es diferente cuando el lenguaje tiene una cardinalidad arbitrariamente grande, ya que, aunque los teoremas de completitud y compacidad siguen siendo demostrablemente equivalentes entre sí en ZF, también son demostrablemente equivalentes a una forma débil del axioma de elección conocido como el lema del ultrafiltro . En particular, ninguna teoría que extienda ZF puede probar los teoremas de completitud o compacidad sobre lenguajes arbitrarios (posiblemente incontables) sin probar también el lema del ultrafiltro sobre un conjunto de la misma cardinalidad.
El teorema de completitud es una propiedad central de la lógica de primer orden que no se cumple para todas las lógicas. La lógica de segundo orden , por ejemplo, no tiene un teorema de completitud para su semántica estándar (aunque sí tiene la propiedad de completitud para la semántica de Henkin ), y el conjunto de fórmulas lógicamente válidas en la lógica de segundo orden no es recursivamente enumerable. Lo mismo es cierto para todas las lógicas de orden superior. Es posible producir sistemas deductivos sólidos para lógicas de orden superior, pero ningún sistema de ese tipo puede ser completo.
El teorema de Lindström establece que la lógica de primer orden es la lógica más fuerte (sujeta a ciertas restricciones) que satisface tanto la compacidad como la completitud.
Se puede demostrar un teorema de completitud para la lógica modal o la lógica intuicionista con respecto a la semántica de Kripke .
La prueba original del teorema de Gödel consistía en reducir el problema a un caso especial para fórmulas en una determinada forma sintáctica y luego manejar esta forma con un argumento ad hoc .
En los textos de lógica modernos, el teorema de completitud de Gödel suele demostrarse con la prueba de Henkin , en lugar de con la prueba original de Gödel. La prueba de Henkin construye directamente un modelo de término para cualquier teoría de primer orden consistente. James Margetson (2004) desarrolló una prueba formal computarizada utilizando el demostrador de teoremas de Isabelle . [4] También se conocen otras pruebas.