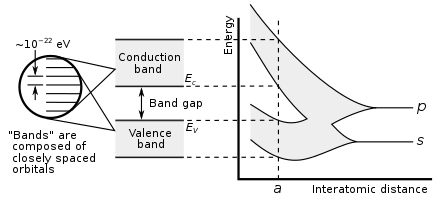
En física y química del estado sólido , una banda prohibida , también llamada banda prohibida o brecha de energía , es un rango de energía en un sólido donde no existen estados electrónicos . En los gráficos de la estructura de bandas electrónicas de los sólidos, la banda prohibida se refiere a la diferencia de energía (a menudo expresada en electronvoltios ) entre la parte superior de la banda de valencia y la parte inferior de la banda de conducción en aisladores y semiconductores . Es la energía necesaria para promover un electrón desde la banda de valencia a la banda de conducción. El electrón resultante de la banda de conducción (y el hueco del electrón en la banda de valencia) pueden moverse libremente dentro de la red cristalina y sirven como portadores de carga para conducir la corriente eléctrica . Está estrechamente relacionado con la brecha HOMO/LUMO en química. Si la banda de valencia está completamente llena y la banda de conducción está completamente vacía, entonces los electrones no pueden moverse dentro del sólido porque no hay estados disponibles. Si los electrones no pueden moverse libremente dentro de la red cristalina, entonces no se genera corriente debido a que no hay movilidad neta del portador de carga. Sin embargo, si algunos electrones se transfieren de la banda de valencia (en su mayoría llena) a la banda de conducción (en su mayoría vacía), entonces puede fluir corriente (ver generación y recombinación de portadores ). Por lo tanto, la banda prohibida es un factor importante que determina la conductividad eléctrica de un sólido. Las sustancias que tienen bandas prohibidas grandes (también llamadas bandas prohibidas "anchas") son generalmente aislantes , aquellas con bandas prohibidas pequeñas (también llamadas bandas prohibidas "estrechas") son semiconductores , y los conductores tienen bandas prohibidas muy pequeñas o ninguna, porque la valencia y Las bandas de conducción se superponen para formar una banda continua.
Cada sólido tiene su propia estructura característica de bandas de energía . Esta variación en la estructura de la banda es responsable de la amplia gama de características eléctricas observadas en diversos materiales. Dependiendo de la dimensión, la estructura de la banda y la espectroscopia pueden variar. Los diferentes tipos de dimensiones son los enumerados: una dimensión, dos dimensiones y tres dimensiones. [1]
En los semiconductores y aislantes, los electrones están confinados a una serie de bandas de energía y prohibidos en otras regiones porque no hay estados electrónicos permitidos que puedan ocupar. El término "banda prohibida" se refiere a la diferencia de energía entre la parte superior de la banda de valencia y la parte inferior de la banda de conducción. Los electrones pueden saltar de una banda a otra. Sin embargo, para que un electrón de la banda de valencia sea promovido a la banda de conducción, se requiere una cantidad mínima específica de energía para la transición. Esta energía requerida es una característica intrínseca del material sólido. Los electrones pueden ganar suficiente energía para saltar a la banda de conducción absorbiendo un fonón (calor) o un fotón (luz).
Un semiconductor es un material con una banda prohibida de tamaño intermedio distinta de cero que se comporta como un aislante a T = 0K, pero permite la excitación térmica de electrones en su banda de conducción a temperaturas inferiores a su punto de fusión. Por el contrario, un material con una banda prohibida grande es un aislante . En los conductores , las bandas de valencia y conducción pueden superponerse, por lo que ya no existe una banda prohibida con regiones prohibidas de estados electrónicos.
La conductividad de los semiconductores intrínsecos depende en gran medida de la banda prohibida. Los únicos portadores de carga disponibles para la conducción son los electrones que tienen suficiente energía térmica para ser excitados a través de la banda prohibida y los huecos de electrones que quedan cuando se produce dicha excitación.
La ingeniería de banda prohibida es el proceso de controlar o alterar la banda prohibida de un material controlando la composición de ciertas aleaciones semiconductoras , como GaAlAs , InGaAs e InAlAs . También es posible construir materiales en capas con composiciones alternas mediante técnicas como la epitaxia de haz molecular . Estos métodos se aprovechan en el diseño de transistores bipolares de heterounión (HBT), diodos láser y células solares .
La distinción entre semiconductores y aislantes es una cuestión de convención. Un enfoque es pensar en los semiconductores como un tipo de aislante con una banda prohibida estrecha. Los aisladores con una banda prohibida mayor, generalmente superior a 4 eV, [2] no se consideran semiconductores y generalmente no exhiben un comportamiento semiconductor en condiciones prácticas. La movilidad de los electrones también juega un papel en la determinación de la clasificación informal de un material.
La energía de banda prohibida de los semiconductores tiende a disminuir al aumentar la temperatura. Cuando la temperatura aumenta, la amplitud de las vibraciones atómicas aumenta, lo que lleva a un mayor espacio interatómico. La interacción entre los fonones de la red y los electrones libres y los huecos también afectará en menor medida a la banda prohibida. [3] La relación entre la energía de la banda prohibida y la temperatura se puede describir mediante la expresión empírica de Varshni (llamada así por YP Varshni ),
Además, las vibraciones de la red aumentan con la temperatura, lo que aumenta el efecto de la dispersión de electrones. Además, el número de portadores de carga dentro de un semiconductor aumentará, ya que más portadores tienen la energía necesaria para cruzar el umbral de la banda prohibida y, por lo tanto, la conductividad de los semiconductores también aumenta al aumentar la temperatura. [5] La presión externa también influye en la estructura electrónica de los semiconductores y, por tanto, en sus bandas prohibidas ópticas. [6]
En un cristal semiconductor normal, la banda prohibida está fija debido a estados de energía continuos. En un cristal de puntos cuánticos , la banda prohibida depende del tamaño y puede modificarse para producir un rango de energías entre la banda de valencia y la banda de conducción. [7] También se le conoce como efecto de confinamiento cuántico .
Las bandas prohibidas pueden ser directas o indirectas , dependiendo de la estructura de bandas electrónicas del material. [6] [8] [9]
Se mencionó anteriormente que las dimensiones tienen diferente estructura de bandas y espectroscopia. Los sólidos no metálicos, que son unidimensionales, tienen propiedades ópticas que dependen de las transiciones electrónicas entre las bandas de valencia y conducción. Además, la probabilidad de transición espectroscópica es entre el orbital inicial y final y depende de la integral. [1] φ i es el orbital inicial, φ f es el orbital final, ʃ φ f * ûεφ i es la integral, ε es el vector eléctrico y u es el momento dipolar. [1]
Las estructuras bidimensionales de sólidos se comportan debido a la superposición de orbitales atómicos. [1] El cristal bidimensional más simple contiene átomos idénticos dispuestos en una red cuadrada. [1] La división de energía ocurre en el borde de la zona de Brillouin para situaciones unidimensionales debido a un potencial periódico débil, que produce una brecha entre las bandas. El comportamiento de las situaciones unidimensionales no ocurre en los casos bidimensionales porque hay libertades de movimiento adicionales. Además, se puede producir una banda prohibida con un fuerte potencial periódico para casos bidimensionales y tridimensionales. [1]
Según su estructura de banda, los materiales se caracterizan por tener una banda prohibida directa o una banda prohibida indirecta. En el modelo de electrones libres, k es el momento de un electrón libre y asume valores únicos dentro de la zona de Brillouin que describe la periodicidad de la red cristalina. Si el impulso del estado de energía más bajo en la banda de conducción y el estado de energía más alto de la banda de valencia de un material tienen el mismo valor, entonces el material tiene una banda prohibida directa. Si no son iguales, entonces el material tiene una banda prohibida indirecta y la transición electrónica debe sufrir una transferencia de impulso para satisfacer la conservación. Estas transiciones indirectas "prohibidas" todavía se producen, aunque con probabilidades muy bajas y con una energía más débil. [6] [8] [9] Para materiales con una banda prohibida directa, los electrones de valencia pueden ser excitados directamente en la banda de conducción por un fotón cuya energía es mayor que la banda prohibida. Por el contrario, para materiales con una banda prohibida indirecta, un fotón y un fonón deben estar involucrados en una transición desde la parte superior de la banda de valencia a la parte inferior de la banda de conducción, lo que implica un cambio de momento . Por lo tanto, los materiales de banda prohibida directa tienden a tener propiedades de absorción y emisión de luz más fuertes y tienden a ser más adecuados para energía fotovoltaica (PV), diodos emisores de luz (LED) y diodos láser ; [10] sin embargo, los materiales de banda prohibida indirecta se utilizan con frecuencia en fotovoltaicos y LED cuando los materiales tienen otras propiedades favorables.
Los LED y los diodos láser suelen emitir fotones con una energía cercana y ligeramente mayor que la banda prohibida del material semiconductor del que están hechos. Por lo tanto, a medida que aumenta la energía de la banda prohibida, el color del LED o del láser cambia de infrarrojo a rojo, a través del arco iris a violeta y luego a UV. [11]
La banda prohibida óptica (ver más abajo) determina qué porción del espectro solar absorbe una célula fotovoltaica . [12] Estrictamente, un semiconductor no absorberá fotones de energía menor que la banda prohibida; mientras que la mayoría de los fotones con energías que exceden la banda prohibida generarán calor. Ninguno de ellos contribuye a la eficiencia de una célula solar. Una forma de solucionar este problema se basa en el llamado concepto de gestión de fotones, en cuyo caso el espectro solar se modifica para adaptarlo al perfil de absorción de la célula solar. [13]
A continuación se muestran los valores de banda prohibida para algunos materiales seleccionados. [14] Para obtener una lista completa de bandas prohibidas en semiconductores, consulte Lista de materiales semiconductores .
En materiales con una gran energía de enlace del excitón , es posible que un fotón tenga apenas suficiente energía para crear un excitón (par electrón-hueco unido), pero no suficiente energía para separar el electrón y el hueco (que se sienten atraídos eléctricamente entre sí). otro). En esta situación, existe una distinción entre "banda prohibida óptica" y "banda prohibida electrónica" (o "brecha de transporte"). La banda prohibida óptica es el umbral para que los fotones sean absorbidos, mientras que la brecha de transporte es el umbral para crear un par electrón-hueco que no está unido. La banda prohibida óptica tiene una energía más baja que la brecha de transporte.
En casi todos los semiconductores inorgánicos, como el silicio, el arseniuro de galio, etc., hay muy poca interacción entre electrones y huecos (energía de unión de excitones muy pequeña) y, por lo tanto, la banda prohibida óptica y electrónica son esencialmente idénticas y la distinción entre ellas es ignorado. Sin embargo, en algunos sistemas, incluidos los semiconductores orgánicos y los nanotubos de carbono de pared simple , la distinción puede ser significativa.
En fotónica , las bandas prohibidas o bandas de parada son rangos de frecuencias de fotones donde, si se desprecian los efectos de túnel, no se pueden transmitir fotones a través de un material. Un material que exhibe este comportamiento se conoce como cristal fotónico . El concepto de hiperuniformidad [22] ha ampliado la gama de materiales de banda prohibida fotónica, más allá de los cristales fotónicos. Aplicando la técnica en mecánica cuántica supersimétrica , se ha sugerido una nueva clase de materiales ópticos desordenados, [23] que soportan bandas prohibidas perfectamente equivalentes a las de los cristales o cuasicristales .
Una física similar se aplica a los fonones en un cristal fonónico . [24]
