Bisección

División de algo en dos partes iguales o congruentes

La línea DE biseca a la línea AB en D, la línea EF es una bisectriz perpendicular del segmento AD en C, y la línea EF es la bisectriz interior del ángulo recto AED

En geometría , la bisección es la división de algo en dos partes iguales o congruentes (que tienen la misma forma y tamaño). Por lo general, se trata de una línea bisectriz , también llamada bisectriz . Los tipos de bisectrices más comúnmente considerados son la bisectriz de segmento , una recta que pasa por el punto medio de un segmento dado , y la bisectriz de ángulo , una recta que pasa por el vértice de un ángulo (que lo divide en dos ángulos iguales). En el espacio tridimensional , la bisección suele realizarse mediante un plano bisector , también llamado bisectriz .

Bisectriz del segmento de recta perpendicular

Definición

Bisectriz perpendicular de un segmento de recta

• La mediatriz de un segmento de recta es una recta que corta al segmento en su punto medio perpendicularmente.
• La mediatriz de un segmento de recta también tiene la propiedad de que cada uno de sus puntos equidista de los extremos del segmento AB: ${\displaystyle AB}$ ${\displaystyle X}$

(D) . ${\displaystyle \quad |XA|=|XB|}$

La prueba se sigue del teorema de Pitágoras : ${\displaystyle }$

${\displaystyle |XA|^{2}=|XM|^{2}+|MA|^{2}=|XM|^{2}+|MB|^{2}=|XB|^{2}\;.}$

La propiedad (D) se suele utilizar para la construcción de una mediatriz:

Construcción con regla y compás.

Construcción con regla y compás.

En geometría clásica, la bisección es una construcción simple con compás y regla , cuya posibilidad depende de la capacidad de trazar arcos de radios iguales y centros diferentes:

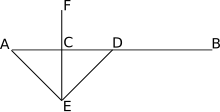
El segmento se biseca dibujando círculos que se cruzan de igual radio , cuyos centros son los puntos finales del segmento. La recta determinada por los puntos de intersección de las dos circunferencias es la bisectriz perpendicular del segmento. Debido a que la construcción de la bisectriz se realiza sin conocer el punto medio del segmento , la construcción se utiliza para determinar la intersección de la bisectriz y el segmento de línea. ${\displaystyle AB}$ ${\displaystyle r>{\tfrac {1}{2}}|AB|}$
${\displaystyle M}$ ${\displaystyle M}$

De hecho, esta construcción se utiliza cuando se construye una línea perpendicular a una línea dada en un punto dado : se dibuja un círculo cuyo centro es tal que corta la línea en dos puntos , y la perpendicular a construir es el segmento que la biseca . ${\displaystyle g}$ ${\displaystyle P}$ ${\displaystyle P}$ ${\displaystyle g}$ ${\displaystyle A,B}$ ${\displaystyle AB}$

Ecuaciones

Si son los vectores de posición de dos puntos , entonces su punto medio es y el vector es un vector normal de la bisectriz del segmento perpendicular. Por tanto su ecuación vectorial es . Insertar y expandir la ecuación conduce a la ecuación vectorial ${\displaystyle {\vec {a}},{\vec {b}}}$ ${\displaystyle A,B}$ ${\displaystyle M:{\vec {m}}={\tfrac {{\vec {a}}+{\vec {b}}}{2}}}$ ${\displaystyle {\vec {a}}-{\vec {b}}}$ ${\displaystyle ({\vec {x}}-{\vec {m}})\cdot ({\vec {a}}-{\vec {b}})=0}$ ${\displaystyle {\vec {m}}=\cdots }$

(V) ${\displaystyle \quad {\vec {x}}\cdot ({\vec {a}}-{\vec {b}})={\tfrac {1}{2}}({\vec {a}}^{2}-{\vec {b}}^{2}).}$

Con uno se obtiene la ecuación en forma de coordenadas: ${\displaystyle A=(a_{1},a_{2}),B=(b_{1},b_{2})}$

(C) ${\displaystyle \quad (a_{1}-b_{1})x+(a_{2}-b_{2})y={\tfrac {1}{2}}(a_{1}^{2}-b_{1}^{2}+a_{2}^{2}-b_{2}^{2})\;.}$

O explícitamente:
(E) , donde , y . ${\displaystyle \quad y=m(x-x_{0})+y_{0}}$
${\displaystyle \;m=-{\tfrac {b_{1}-a_{1}}{b_{2}-a_{2}}}}$ ${\displaystyle \;x_{0}={\tfrac {1}{2}}(a_{1}+b_{1})\;}$ ${\displaystyle \;y_{0}={\tfrac {1}{2}}(a_{2}+b_{2})\;}$

Aplicaciones

Se utilizaron bisectrices de segmentos perpendiculares para resolver varios problemas geométricos:

1. Construcción del centro de un círculo de Tales .
2. Construcción del centro de la excircunferencia de un triángulo,
3. Los límites del diagrama de Voronoi constan de segmentos de dichas líneas o planos.

Plano bisector

Bisectrices de un segmento de recta perpendicular en el espacio

• La mediatriz de un segmento de recta es un plano que corta al segmento en su punto medio perpendicularmente.

Su ecuación vectorial es literalmente la misma que en el caso del plano:

(V) ${\displaystyle \quad {\vec {x}}\cdot ({\vec {a}}-{\vec {b}})={\tfrac {1}{2}}({\vec {a}}^{2}-{\vec {b}}^{2}).}$

Con uno se obtiene la ecuación en forma de coordenadas: ${\displaystyle A=(a_{1},a_{2},a_{3}),B=(b_{1},b_{2},b_{3})}$

(C3) ${\displaystyle \quad (a_{1}-b_{1})x+(a_{2}-b_{2})y+(a_{3}-b_{3})z={\tfrac {1}{2}}(a_{1}^{2}-b_{1}^{2}+a_{2}^{2}-b_{2}^{2}+a_{3}^{2}-b_{3}^{2})\;.}$

La propiedad (D) (ver arriba) también es literalmente cierta en el espacio:
(D) El plano bisector perpendicular de un segmento tiene para cualquier punto la propiedad: . ${\displaystyle AB}$ ${\displaystyle X}$ ${\displaystyle \;|XA|=|XB|}$

Bisectriz

Bisección de un ángulo con compás y regla

Una bisectriz de ángulo divide el ángulo en dos ángulos de medidas iguales . Un ángulo sólo tiene una bisectriz. Cada punto de la bisectriz de un ángulo equidista de los lados del ángulo.

La 'interior' o 'bisectriz interna' de un ángulo es la recta, media recta o segmento de recta que divide un ángulo de menos de 180° en dos ángulos iguales. La 'exterior' o 'bisectriz externa' es la recta que divide el ángulo suplementario (de 180° menos el ángulo original), formado por un lado que forma el ángulo original y la extensión del otro lado, en dos ángulos iguales. ^[1]

Para bisecar un ángulo con regla y compás , se dibuja un círculo cuyo centro es el vértice. El círculo se encuentra con el ángulo en dos puntos: uno en cada cateto. Usando cada uno de estos puntos como centro, dibuja dos círculos del mismo tamaño. La intersección de los círculos (dos puntos) determina una recta que es la bisectriz del ángulo.

La prueba de la exactitud de esta construcción es bastante intuitiva y se basa en la simetría del problema. La trisección de un ángulo (dividiéndolo en tres partes iguales) no se puede lograr sólo con el compás y la regla (esto lo demostró por primera vez Pierre Wantzel ).

Las bisectrices interna y externa de un ángulo son perpendiculares . Si el ángulo está formado por las dos rectas dadas algebraicamente como y entonces las bisectrices interna y externa están dadas por las dos ecuaciones ^{[2] : p.15} ${\displaystyle l_{1}x+m_{1}y+n_{1}=0}$ ${\displaystyle l_{2}x+m_{2}y+n_{2}=0,}$

${\displaystyle {\frac {l_{1}x+m_{1}y+n_{1}}{\sqrt {l_{1}^{2}+m_{1}^{2}}}}=\pm {\frac {l_{2}x+m_{2}y+n_{2}}{\sqrt {l_{2}^{2}+m_{2}^{2}}}}.}$

Triángulo

Concurrencias y colinealidades

Las bisectrices de los ángulos interiores de un triángulo son concurrentes en un punto llamado incentro del triángulo, como se ve en el diagrama.

Las bisectrices de dos ángulos exteriores y la bisectriz del otro ángulo interior son concurrentes. ^{[3] : pág.149}

Tres puntos de intersección, cada uno de una bisectriz de ángulo externo con el lado extendido opuesto , son colineales (caen en la misma línea entre sí). ^{[3] : pág. 149}

Tres puntos de intersección, dos de ellos entre una bisectriz de un ángulo interior y el lado opuesto, y el tercero entre la otra bisectriz de un ángulo exterior y el lado opuesto extendido, son colineales. ^{[3] : pág. 149}

Teorema de la bisectriz del ángulo

En este diagrama, BD:DC = AB:AC.

El teorema de la bisectriz del ángulo se refiere a las longitudes relativas de los dos segmentos en los que se divide el lado de un triángulo por una línea que biseca el ángulo opuesto. Iguala sus longitudes relativas a las longitudes relativas de los otros dos lados del triángulo.

Longitudes

Si las longitudes de los lados de un triángulo son , el semiperímetro y A es el ángulo opuesto al lado , entonces la longitud de la bisectriz interna del ángulo A es ^{[3] : p. 70} ${\displaystyle a,b,c}$ ${\displaystyle s=(a+b+c)/2,}$ ${\displaystyle a}$

${\displaystyle {\frac {2{\sqrt {bcs(s-a)}}}{b+c}},}$

o en términos trigonométricos, ^[4]

${\displaystyle {\frac {2bc}{b+c}}\cos {\frac {A}{2}}.}$

Si la bisectriz interna del ángulo A en el triángulo ABC tiene longitud y si esta bisectriz divide el lado opuesto a A en segmentos de longitudes m y n , entonces ^{[3] : p.70} ${\displaystyle t_{a}}$

${\displaystyle t_{a}^{2}+mn=bc}$

donde byc son las longitudes de los lados opuestos a los vértices B y C; y el lado opuesto a A se divide en la proporción b : c .

Si las bisectrices internas de los ángulos A, B y C tienen longitudes y , entonces ^[5] ${\displaystyle t_{a},t_{b},}$ ${\displaystyle t_{c}}$

${\displaystyle {\frac {(b+c)^{2}}{bc}}t_{a}^{2}+{\frac {(c+a)^{2}}{ca}}t_{b}^{2}+{\frac {(a+b)^{2}}{ab}}t_{c}^{2}=(a+b+c)^{2}.}$

No hay dos triángulos no congruentes que compartan el mismo conjunto de tres longitudes de bisectriz de ángulo interno. ^{[6] [7]}

Triángulos enteros

Existen triángulos enteros con bisectriz de ángulo racional .

Cuadrilátero

Las bisectrices de ángulos internos de un cuadrilátero convexo forman un cuadrilátero cíclico (es decir, los cuatro puntos de intersección de bisectrices de ángulos adyacentes son concíclicos ), ^[8] o son concurrentes . En este último caso el cuadrilátero es un cuadrilátero tangencial .

Rombo

Cada diagonal de un rombo biseca ángulos opuestos.

Cuadrilátero extangencial

El excentro de un cuadrilátero extangencial se encuentra en la intersección de seis bisectrices. Estas son las bisectrices de los ángulos internos en dos ángulos de vértice opuestos, las bisectrices de ángulos externos (bisectrices de ángulos suplementarios) en los otros dos ángulos de vértices y las bisectrices de ángulos externos en los ángulos formados donde se cruzan las extensiones de los lados opuestos .

Parábola

La tangente a una parábola en cualquier punto biseca el ángulo entre la línea que une el punto con el foco y la línea que va desde el punto y es perpendicular a la directriz.

Bisectrices de los lados de un polígono

Triángulo

Medianas

Cada una de las tres medianas de un triángulo es un segmento de línea que pasa por un vértice y el punto medio del lado opuesto, por lo que biseca ese lado (aunque en general no es perpendicular). Las tres medianas se cortan en un punto que se llama centroide del triángulo, que es su centro de masa si tiene densidad uniforme; por lo tanto, cualquier línea que pase por el centroide de un triángulo y uno de sus vértices biseca el lado opuesto. El centroide está dos veces más cerca del punto medio de cualquier lado que del vértice opuesto.

Bisectrices perpendiculares

La bisectriz perpendicular interior de un lado de un triángulo es el segmento, que cae enteramente sobre y dentro del triángulo, de la línea que biseca perpendicularmente ese lado. Las tres bisectrices perpendiculares de los tres lados de un triángulo se cruzan en el circuncentro (el centro del círculo que pasa por los tres vértices). Por lo tanto, cualquier línea que pase por el circuncentro de un triángulo y sea perpendicular a un lado biseca ese lado.

En un triángulo agudo el circuncentro divide las bisectrices perpendiculares interiores de los dos lados más cortos en proporciones iguales. En un triángulo obtuso, las bisectrices perpendiculares de los dos lados más cortos (extendidas más allá de sus lados opuestos del triángulo hasta el circuncentro) se dividen por sus respectivos lados del triángulo que se cruzan en proporciones iguales. ^{[9] : Corolarios 5 y 6}

Para cualquier triángulo, las bisectrices perpendiculares interiores están dadas por y donde están los lados y el área es ^{[9] : Thm 2} ${\displaystyle p_{a}={\tfrac {2aT}{a^{2}+b^{2}-c^{2}}},}$ ${\displaystyle p_{b}={\tfrac {2bT}{a^{2}+b^{2}-c^{2}}},}$ ${\displaystyle p_{c}={\tfrac {2cT}{a^{2}-b^{2}+c^{2}}},}$ ${\displaystyle a\geq b\geq c}$ ${\displaystyle T.}$

Cuadrilátero

Las dos bimedianas de un cuadrilátero convexo son los segmentos de recta que conectan los puntos medios de los lados opuestos, por lo que cada uno bisecciona dos lados. Las dos bimedianas y el segmento de recta que une los puntos medios de las diagonales son concurrentes en un punto llamado "centroide del vértice" y todos son bisecados por este punto. ^{[10] : pág.125}

Las cuatro "maltitudes" de un cuadrilátero convexo son las perpendiculares a un lado que pasan por el punto medio del lado opuesto, por lo que dividen este último lado. Si el cuadrilátero es cíclico (inscrito en un círculo), estas maltitudes son concurrentes en (todas se encuentran en) un punto común llamado "anticentro".

El teorema de Brahmagupta establece que si un cuadrilátero cíclico es ortodiagonal (es decir, tiene diagonales perpendiculares ), entonces la perpendicular a un lado desde el punto de intersección de las diagonales siempre biseca el lado opuesto.

La construcción de la bisectriz perpendicular forma un cuadrilátero a partir de las bisectrices perpendiculares de los lados de otro cuadrilátero.

Bisectrices de área y bisectrices de perímetro

Triángulo

Hay una infinidad de rectas que bisecan el área de un triángulo . Tres de ellas son las medianas del triángulo (que conectan los puntos medios de los lados con los vértices opuestos), y éstas son concurrentes en el centroide del triángulo ; de hecho, son las únicas bisectrices de área que pasan por el centroide. Otras tres bisectrices de área son paralelas a los lados del triángulo; cada uno de estos cruza los otros dos lados para dividirlos en segmentos con las proporciones . ^[11] Estas seis líneas son concurrentes de tres en tres: además de que las tres medianas son concurrentes, cualquier mediana es concurrente con dos de las bisectrices de áreas paralelas laterales. ${\displaystyle {\sqrt {2}}+1:1}$

La envolvente de la infinitud de bisectrices de área es un deltoides (definido ampliamente como una figura con tres vértices conectados por curvas que son cóncavas al exterior del deltoides, haciendo que los puntos interiores sean un conjunto no convexo). ^[11] Los vértices del deltoides están en los puntos medios de las medianas; Todos los puntos dentro del deltoides están en tres bisectrices de área diferentes, mientras que todos los puntos fuera de él están en solo una. [1] Los lados del deltoides son arcos de hipérbolas que son asintóticos a los lados extendidos del triángulo. ^[11] La relación entre el área de la envolvente de las bisectrices y el área del triángulo es invariante para todos los triángulos y es igual a 0,019860... o menos del 2%. ${\displaystyle {\tfrac {3}{4}}\log _{e}(2)-{\tfrac {1}{2}},}$

Una cuchilla de triángulo es un segmento de línea que biseca el perímetro del triángulo y tiene un punto final en el punto medio de uno de los tres lados. Las tres cuchillas concurren en (todas pasan por) el centro del círculo de Spieker , que es el círculo interior del triángulo medial . Las cuchillas son paralelas a las bisectrices del ángulo.

Un divisor de un triángulo es un segmento de línea que tiene un extremo en uno de los tres vértices del triángulo y biseca el perímetro. Los tres divisores concurren en el punto Nagel del triángulo.

Cualquier línea que pase por un triángulo y que divida el área del triángulo y su perímetro por la mitad pasa por el incentro del triángulo (el centro de su circunferencia ). Hay uno, dos o tres de estos para cualquier triángulo determinado. Una línea que pasa por el incentro biseca uno del área o perímetro si y sólo si también biseca al otro. ^[12]

Paralelogramo

Cualquier línea que pase por el punto medio de un paralelogramo biseca el área ^[11] y el perímetro.

Circulo y elipse

Todas las bisectrices de área y de perímetro de un círculo u otra elipse pasan por el centro , y cualquier cuerda que pase por el centro bisecta el área y el perímetro. En el caso de un círculo son los diámetros del círculo.

Bisectrices de diagonales

Paralelogramo

Las diagonales de un paralelogramo se bisecan entre sí.

Cuadrilátero

Si un segmento de línea que conecta las diagonales de un cuadrilátero biseca ambas diagonales, entonces este segmento de línea (la línea de Newton ) es a su vez bisectado por el centroide del vértice.

Bisectrices de volumen

Un plano que divide dos aristas opuestas de un tetraedro en una proporción determinada también divide el volumen del tetraedro en la misma proporción. Por lo tanto, cualquier plano que contenga una bimediana (conector de los puntos medios de los bordes opuestos) de un tetraedro biseca el volumen del tetraedro ^{[13] [14] : págs.89–90}

Referencias

1. Weisstein, Eric W. "Bisectriz del ángulo exterior". De MathWorld: un recurso web de Wolfram.
2. España, Barry. Cónicas analíticas , Publicaciones de Dover, 2007 (orig. 1957).
3. Johnson, Roger A., ​​Geometría euclidiana avanzada , Dover Publ., 2007 (orig. 1929).
4. Oxman, Víctor. "Sobre la existencia de triángulos con longitudes dadas de un lado y dos bisectrices de ángulos adyacentes", Forum Geometriorum 4, 2004, 215-218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf
5. Simons, Estuardo. Gaceta Matemática 93, marzo de 2009, 115-116.
6. Mironescu, P. y Panaitopol, L., "La existencia de un triángulo con longitudes prescritas de bisectriz de ángulo", American Mathematical Monthly 101 (1994): 58–60.
7. Oxman, Victor, "Una prueba puramente geométrica de la unicidad de un triángulo con bisectrices prescritas", Forum Geometriorum 8 (2008): 197–200.
8. Weisstein, Eric W. "Cuadrilátero". De MathWorld: un recurso web de Wolfram. http://mathworld.wolfram.com/Quadrilateral.html
9. Mitchell, Douglas W. (2013), "Bisectrices perpendiculares de lados de triángulos", Forum Geometriorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf
10. Altshiller-Court, Nathan, Geometría universitaria , Dover Publ., 2007.
11. Dunn, Jas. A.; Bonita, Jas. E. (mayo de 1972). "Reducir a la mitad un triángulo". La Gaceta Matemática . 56 (396): 105-108. doi :10.2307/3615256. JSTOR  3615256.
12. Kodokostas, Dimitrios, "Triangle Equalizers", Mathematics Magazine 83, abril de 2010, págs.
13. Weisstein, Eric W. "Tetraedro". De MathWorld: un recurso web de Wolfram. http://mathworld.wolfram.com/Tetrahedron.html
14. Altshiller-Court, N. "El tetraedro". Cap. 4 en Geometría sólida pura moderna : Chelsea, 1979.

enlaces externos

• La bisectriz del ángulo en cortar el nudo
• Definición de bisectriz de ángulo. Referencia abierta de matemáticas con subprograma interactivo
• Definición de recta bisectriz. Referencia abierta de matemáticas con subprograma interactivo
• Bisectriz de la recta perpendicular. Con subprograma interactivo
• Instrucciones animadas para dividir un ángulo y una línea usando un compás y una regla
• Weisstein, Eric W. "Línea bisectriz". MundoMatemático .

Este artículo incorpora material de Bisectriz del ángulo en PlanetMath , que tiene la licencia Creative Commons Attribution/Share-Alike License .