La física computacional es el estudio y la implementación del análisis numérico para resolver problemas de física . [1] Históricamente, la física computacional fue la primera aplicación de las computadoras modernas en la ciencia, y ahora es un subconjunto de la ciencia computacional . A veces se la considera una subdisciplina (o rama) de la física teórica , pero otros la consideran una rama intermedia entre la física teórica y la experimental , un área de estudio que complementa tanto la teoría como la experimentación. [2]
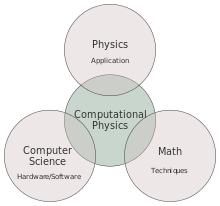
En física, diferentes teorías basadas en modelos matemáticos proporcionan predicciones muy precisas sobre cómo se comportan los sistemas. Desafortunadamente, a menudo ocurre que no es posible resolver el modelo matemático de un sistema en particular para producir una predicción útil. Esto puede ocurrir, por ejemplo, cuando la solución no tiene una expresión de forma cerrada o es demasiado complicada. En tales casos, se requieren aproximaciones numéricas. La física computacional es la materia que se ocupa de estas aproximaciones numéricas: la aproximación de la solución se escribe como un número finito (y típicamente grande) de operaciones matemáticas simples ( algoritmo ), y se utiliza una computadora para realizar estas operaciones y calcular una solución aproximada y el error respectivo . [1]
Existe un debate sobre el estatus de la computación dentro del método científico. [4] A veces se la considera más afín a la física teórica; otros consideran la simulación por computadora como " experimentos informáticos ", [4] pero otros la consideran una rama intermedia o diferente entre la física teórica y la experimental , una tercera vía que complementa la teoría y el experimento. Si bien las computadoras se pueden utilizar en experimentos para la medición y el registro (y almacenamiento) de datos, esto claramente no constituye un enfoque computacional.
Los problemas de física computacional son en general muy difíciles de resolver con exactitud. Esto se debe a varias razones (matemáticas): falta de solubilidad algebraica y/o analítica, complejidad y caos. Por ejemplo, incluso problemas aparentemente simples, como calcular la función de onda de un electrón que orbita un átomo en un campo eléctrico fuerte ( efecto Stark ), pueden requerir un gran esfuerzo para formular un algoritmo práctico (si se puede encontrar uno); pueden requerirse otras técnicas más crudas o de fuerza bruta, como métodos gráficos o búsqueda de raíces . En el lado más avanzado, a veces también se utiliza la teoría de perturbación matemática (se muestra un funcionamiento para este ejemplo particular aquí ). Además, el costo computacional y la complejidad computacional para problemas de muchos cuerpos (y sus contrapartes clásicas ) tienden a crecer rápidamente. Un sistema macroscópico normalmente tiene un tamaño del orden de partículas constituyentes, por lo que es algo problemático. La resolución de problemas mecánicos cuánticos es generalmente de orden exponencial en el tamaño del sistema [5] y para N-cuerpos clásicos es de orden N-cuadrado. Por último, muchos sistemas físicos son inherentemente no lineales en el mejor de los casos y, en el peor, caóticos : esto significa que puede ser difícil garantizar que los errores numéricos no crezcan hasta el punto de hacer que la "solución" sea inútil. [6]
Dado que la física computacional utiliza una amplia clase de problemas, generalmente se divide entre los diferentes problemas matemáticos que resuelve numéricamente o los métodos que aplica. Entre ellos, se pueden considerar:
Todos estos métodos (y varios otros) se utilizan para calcular las propiedades físicas de los sistemas modelados.
La física computacional también toma prestadas algunas ideas de la química computacional : por ejemplo, la teoría del funcional de la densidad utilizada por los físicos computacionales del estado sólido para calcular las propiedades de los sólidos es básicamente la misma que la utilizada por los químicos para calcular las propiedades de las moléculas.
Además, la física computacional abarca el ajuste de la estructura del software / hardware para resolver los problemas (ya que los problemas normalmente pueden ser muy grandes, en necesidad de potencia de procesamiento o en solicitudes de memoria ).
Es posible encontrar una rama computacional correspondiente para cada campo principal de la física:
Debido a la amplia clase de problemas que trata la física computacional, es un componente esencial de la investigación moderna en diferentes áreas de la física, a saber: física de aceleradores , astrofísica , teoría general de la relatividad (a través de la relatividad numérica ), mecánica de fluidos ( dinámica de fluidos computacional ), teoría de campos reticulares / teoría de calibres reticulares (especialmente cromodinámica cuántica reticular ), física del plasma (ver modelado de plasma ), simulación de sistemas físicos (usando, por ejemplo, dinámica molecular ), códigos informáticos de ingeniería nuclear , predicción de la estructura de proteínas , predicción del tiempo , física del estado sólido , física de la materia condensada blanda , física de impacto a hipervelocidad, etc.
La física computacional del estado sólido, por ejemplo, utiliza la teoría funcional de la densidad para calcular las propiedades de los sólidos, un método similar al que utilizan los químicos para estudiar las moléculas. Otras magnitudes de interés en la física del estado sólido, como la estructura de bandas electrónicas, las propiedades magnéticas y las densidades de carga, se pueden calcular mediante este y otros métodos, incluidos el método de Luttinger-Kohn / kp y los métodos ab-initio .
Además del software de física avanzado, también hay una gran cantidad de herramientas de análisis disponibles para estudiantes principiantes de física, como el software PASCO Capstone.