La ascensión recta (abreviada RA ; símbolo α ) es la distancia angular de un punto particular medida hacia el este a lo largo del ecuador celeste desde el Sol en el equinoccio de marzo hasta el ( círculo horario del) punto en cuestión sobre la Tierra. [1] Cuando se combinan con la declinación , estas coordenadas astronómicas especifican la ubicación de un punto en la esfera celeste en el sistema de coordenadas ecuatoriales .
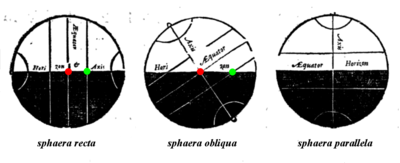
Un término antiguo, ascensión recta ( en latín : ascensio recta ) [2] se refiere a la ascensión , o el punto en el ecuador celeste que se eleva con cualquier objeto celeste visto desde el ecuador de la Tierra , donde el ecuador celeste interseca el horizonte en un ángulo recto . Contrasta con la ascensión oblicua , el punto en el ecuador celeste que se eleva con cualquier objeto celeste visto desde la mayoría de las latitudes de la Tierra, donde el ecuador celeste interseca el horizonte en un ángulo oblicuo . [3]


La ascensión recta es el equivalente celestial de la longitud terrestre . Tanto la ascensión recta como la longitud miden un ángulo desde una dirección primaria (un punto cero) en un ecuador . La ascensión recta se mide desde el Sol en el equinoccio de marzo , es decir, el Primer Punto de Aries , que es el lugar en la esfera celeste donde el Sol cruza el ecuador celeste de sur a norte en el equinoccio de marzo y actualmente se encuentra en la constelación de Piscis . La ascensión recta se mide continuamente en un círculo completo desde esa alineación de la Tierra y el Sol en el espacio, ese equinoccio, y la medida aumenta hacia el este. [4]
Vistos desde la Tierra (excepto en los polos), los objetos con una AR de 12 h son visibles durante más tiempo (aparecen durante toda la noche) en el equinoccio de marzo; aquellos con una AR de 0 h (aparte del Sol) lo son en el equinoccio de septiembre. En esas fechas, a medianoche, dichos objetos alcanzarán ("culminarán" en) su punto más alto (su meridiano). La altura depende de su declinación; si la declinación es de 0° (es decir, en el ecuador celeste ), entonces en el ecuador de la Tierra están directamente sobre la cabeza (en el cenit ).
Se podría haber elegido cualquier unidad angular para la ascensión recta, pero habitualmente se mide en horas ( h ), minutos ( m ) y segundos ( s ), siendo 24 h equivalentes a un círculo completo . Los astrónomos han elegido esta unidad para medir la ascensión recta porque miden la ubicación de una estrella cronometrando su paso por el punto más alto del cielo a medida que la Tierra gira . La línea que pasa por el punto más alto del cielo, llamada meridiano , es la proyección de una línea de longitud sobre la esfera celeste. Dado que un círculo completo contiene 24 h de ascensión recta o 360° ( grados de arco ), 1/24 de un círculo se mide como 1 h de ascensión recta, o 15°; 1/1440 de un círculo se mide como 1 m de ascensión recta, o 15 minutos de arco (también escrito como 15′); y 1/86400 de un círculo contiene 1 s de ascensión recta, o 15 segundos de arco (también escrito como 15″). Un círculo completo, medido en unidades de ascensión recta, contiene 24 × 60 × 60 =86 400 s , o 24 × 60 =1 440 m , o 24 h . [5]
Como las ascensiones rectas se miden en horas (de rotación de la Tierra ), se pueden utilizar para cronometrar las posiciones de los objetos en el cielo. Por ejemplo, si una estrella con AR = 1 h 30 m 00 s está en su meridiano, entonces una estrella con AR = 20 h 00 m 00 s estará en su meridiano (en su punto más alto aparente) 18,5 horas siderales más tarde.
El ángulo horario sideral, utilizado en la navegación astronómica , es similar a la ascensión recta pero aumenta hacia el oeste en lugar de hacia el este. Generalmente se mide en grados (°) y es el complemento de la ascensión recta con respecto a 24 h . [6] Es importante no confundir el ángulo horario sideral con el concepto astronómico de ángulo horario , que mide la distancia angular de un objeto hacia el oeste desde el meridiano local .
El eje de la Tierra traza un pequeño círculo (en relación con su ecuador celeste) lentamente hacia el oeste alrededor de los polos celestes , completando un ciclo en unos 26.000 años. Este movimiento, conocido como precesión , hace que las coordenadas de los objetos celestes estacionarios cambien continuamente, aunque de forma bastante lenta. Por lo tanto, las coordenadas ecuatoriales (incluida la ascensión recta) son inherentemente relativas al año de su observación, y los astrónomos las especifican con referencia a un año particular, conocido como época . Las coordenadas de diferentes épocas deben rotarse matemáticamente para que coincidan entre sí, o para que coincidan con una época estándar. [7] La ascensión recta para las "estrellas fijas" en el ecuador aumenta alrededor de 3,1 segundos por año o 5,1 minutos por siglo, pero para las estrellas fijas alejadas del ecuador la tasa de cambio puede ser cualquier cosa desde el infinito negativo hasta el infinito positivo. (A esto hay que añadir el movimiento propio de una estrella.) A lo largo de un ciclo de precesión de 26.000 años, las "estrellas fijas" que están lejos de los polos eclípticos aumentan su ascensión recta en 24 h, o unos 5,6' por siglo, mientras que las estrellas a 23,5° de un polo eclíptico experimentan un cambio neto de 0 h. La ascensión recta de Polaris aumenta rápidamente: en el año 2000 d. C. era de 2,5 h, pero cuando se acerque al polo norte celeste en 2100, su ascensión recta será de 6 h. El polo norte eclíptico en Draco y el polo sur eclíptico en Dorado siempre están en ascensión recta de 18 h y 6 h respectivamente.
La época estándar utilizada actualmente es J2000.0 , que corresponde al 1 de enero de 2000 a las 12:00 TT . El prefijo "J" indica que se trata de una época juliana . Antes de J2000.0, los astrónomos utilizaban las sucesivas épocas besselianas B1875.0, B1900.0 y B1950.0. [8]
El concepto de ascensión recta se conoce al menos desde Hiparco, quien midió las estrellas en coordenadas ecuatoriales en el siglo II a. C. Pero Hiparco y sus sucesores hicieron sus catálogos de estrellas en coordenadas eclípticas , y el uso de AR se limitó a casos especiales.
Con la invención del telescopio , los astrónomos pudieron observar los objetos celestes con mayor detalle, siempre que el telescopio pudiera mantenerse apuntando al objeto durante un período de tiempo. La forma más fácil de hacerlo es utilizar una montura ecuatorial , que permite alinear el telescopio con uno de sus dos pivotes paralelos al eje de la Tierra. A menudo se utiliza un mecanismo de reloj motorizado con una montura ecuatorial para cancelar la rotación de la Tierra . A medida que la montura ecuatorial se adoptó ampliamente para la observación, el sistema de coordenadas ecuatorial, que incluye la ascensión recta, se adoptó al mismo tiempo por simplicidad. Las monturas ecuatoriales pudieron entonces apuntar con precisión a objetos con ascensión recta y declinación conocidas mediante el uso de círculos de ajuste . El primer catálogo de estrellas que utilizó la ascensión recta y la declinación fue la Historia Coelestis Britannica de John Flamsteed (1712, 1725).
