Aprendizaje automático cuántico

Área de investigación interdisciplinaria en la intersección de la física cuántica y el aprendizaje automático

El aprendizaje automático cuántico es la integración de algoritmos cuánticos dentro de programas de aprendizaje automático . ^{[1] [2] [3] [4] [5] [6] [7] [8]}

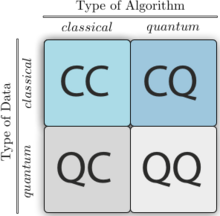
El uso más común del término se refiere a algoritmos de aprendizaje automático para el análisis de datos clásicos ejecutados en una computadora cuántica , es decir, aprendizaje automático mejorado cuánticamente. ^{[9] [10] [11]} Mientras que los algoritmos de aprendizaje automático se utilizan para calcular inmensas cantidades de datos, el aprendizaje automático cuántico utiliza qubits y operaciones cuánticas o sistemas cuánticos especializados para mejorar la velocidad computacional y el almacenamiento de datos realizado por algoritmos en un programa. ^[12] Esto incluye métodos híbridos que involucran procesamiento clásico y cuántico, donde las subrutinas computacionalmente difíciles se subcontratan a un dispositivo cuántico. ^{[13] [14] [15]} Estas rutinas pueden ser de naturaleza más compleja y ejecutarse más rápido en una computadora cuántica. ^[7] Además, los algoritmos cuánticos se pueden utilizar para analizar estados cuánticos en lugar de datos clásicos. ^{[16] [17]}

Más allá de la computación cuántica, el término "aprendizaje automático cuántico" también se asocia con los métodos clásicos de aprendizaje automático aplicados a datos generados a partir de experimentos cuánticos (es decir, aprendizaje automático de sistemas cuánticos ), como el aprendizaje de las transiciones de fase de un sistema cuántico ^{[18] [19]} o la creación de nuevos experimentos cuánticos. ^{[20] [21] [22]}

El aprendizaje automático cuántico también se extiende a una rama de investigación que explora las similitudes metodológicas y estructurales entre ciertos sistemas físicos y sistemas de aprendizaje, en particular las redes neuronales. Por ejemplo, algunas técnicas matemáticas y numéricas de la física cuántica son aplicables al aprendizaje profundo clásico y viceversa. ^{[23] [24] [25]}

Además, los investigadores investigan nociones más abstractas de la teoría del aprendizaje con respecto a la información cuántica, a veces denominada "teoría del aprendizaje cuántico". ^{[26] [27]}

Cuatro enfoques diferentes para combinar las disciplinas de la computación cuántica y el aprendizaje automático. ^{[28] [29]} La primera letra se refiere a si el sistema en estudio es clásico o cuántico, mientras que la segunda letra define si se utiliza un dispositivo de procesamiento de información clásico o cuántico.

Aprendizaje automático con ordenadores cuánticos

El aprendizaje automático mejorado cuánticamente se refiere a algoritmos cuánticos que resuelven tareas de aprendizaje automático, mejorando y a menudo acelerando las técnicas clásicas de aprendizaje automático. Estos algoritmos suelen requerir que se codifique el conjunto de datos clásicos dado en una computadora cuántica para que sea accesible para el procesamiento de información cuántica. Posteriormente, se aplican rutinas de procesamiento de información cuántica y el resultado del cálculo cuántico se lee midiendo el sistema cuántico. Por ejemplo, el resultado de la medición de un cúbit revela el resultado de una tarea de clasificación binaria. Si bien muchas propuestas de algoritmos de aprendizaje automático cuántico aún son puramente teóricas y requieren una computadora cuántica universal a gran escala para ser probadas, otras se han implementado en dispositivos cuánticos de pequeña escala o de propósito especial.

Memorias asociativas cuánticas y reconocimiento de patrones cuánticos

Las memorias asociativas (o memorias direccionables por contenido) son capaces de reconocer el contenido almacenado basándose en una medida de similitud, en lugar de direcciones fijas, como en las memorias de acceso aleatorio. Por ello, deben poder recuperar patrones tanto incompletos como corruptos, la tarea esencial del aprendizaje automático de reconocimiento de patrones.

Las memorias asociativas clásicas típicas almacenan p patrones en las interacciones (sinapsis) de una matriz de energía real y simétrica sobre una red de n neuronas artificiales. La codificación es tal que los patrones deseados son mínimos locales del funcional energético y la recuperación se realiza minimizando la energía total, a partir de una configuración inicial. ${\displaystyle O(n^{2})}$

Lamentablemente, las memorias asociativas clásicas están severamente limitadas por el fenómeno de la diafonía . Cuando se almacenan demasiados patrones, aparecen recuerdos espurios que proliferan rápidamente, de modo que el paisaje energético se desordena y ya no es posible recuperarlos. El número de patrones almacenables suele estar limitado por una función lineal del número de neuronas . ${\displaystyle p\leq O(n)}$

Las memorias asociativas cuánticas ^{[2] [3] [4]} (en su realización más simple) almacenan patrones en una matriz unitaria U que actúa sobre el espacio de Hilbert de n qubits. La recuperación se realiza mediante la evolución unitaria de un estado inicial fijo a una superposición cuántica de los patrones deseados con una distribución de probabilidad máxima en el patrón más similar a una entrada. Por su propia naturaleza cuántica, el proceso de recuperación es, por tanto, probabilístico. Sin embargo, como las memorias asociativas cuánticas están libres de interferencias, nunca se generan memorias espurias. En consecuencia, tienen una capacidad superior a las clásicas. El número de parámetros en la matriz unitaria U es . Por tanto, se pueden tener memorias asociativas cuánticas eficientes y libres de memoria espuria para cualquier número polinómico de patrones. ${\displaystyle O(pn)}$

Simulación de álgebra lineal con amplitudes cuánticas

Varios algoritmos cuánticos para el aprendizaje automático se basan en la idea de codificación de amplitud, es decir, asociar las amplitudes de un estado cuántico con las entradas y salidas de los cálculos. ^{[30] [31] [32]} Dado que un estado de qubits se describe mediante amplitudes complejas, esta codificación de información puede permitir una representación exponencialmente compacta. Intuitivamente, esto corresponde a asociar una distribución de probabilidad discreta sobre variables aleatorias binarias con un vector clásico. El objetivo de los algoritmos basados ​​en la codificación de amplitud es formular algoritmos cuánticos cuyos recursos crezcan polinomialmente en el número de qubits , lo que equivale a una complejidad temporal logarítmica en el número de amplitudes y, por lo tanto, la dimensión de la entrada. ${\displaystyle n}$ ${\displaystyle 2^{n}}$ ${\displaystyle n}$

Muchos algoritmos de aprendizaje automático cuántico en esta categoría se basan en variaciones del algoritmo cuántico para sistemas lineales de ecuaciones ^[33] (coloquialmente llamado HHL, en honor a los autores del artículo) que, bajo condiciones específicas, realiza una inversión de matriz utilizando una cantidad de recursos físicos que crece solo logarítmicamente en las dimensiones de la matriz. Una de estas condiciones es que un hamiltoniano que corresponde a la matriz por entrada se puede simular de manera eficiente, lo que se sabe que es posible si la matriz es dispersa ^[34] o de rango bajo. ^[35] Como referencia, cualquier algoritmo clásico conocido para la inversión de matrices requiere una cantidad de operaciones que crece más que cuadráticamente en la dimensión de la matriz (por ejemplo, ), pero no están restringidas a matrices dispersas. ${\displaystyle O{\mathord {\left(n^{2.373}\right)}}}$

La inversión de matrices cuánticas se puede aplicar a métodos de aprendizaje automático en los que el entrenamiento se reduce a la solución de un sistema lineal de ecuaciones , por ejemplo, en la regresión lineal de mínimos cuadrados, ^{[31] [32]} la versión de mínimos cuadrados de las máquinas de vectores de soporte , ^[30] y los procesos gaussianos. ^[36]

Un obstáculo crucial para los métodos que simulan cálculos de álgebra lineal con las amplitudes de estados cuánticos es la preparación de estados, que a menudo requiere inicializar un sistema cuántico en un estado cuyas amplitudes reflejen las características de todo el conjunto de datos. Aunque se conocen métodos eficientes para la preparación de estados para casos específicos, ^{[37] [38]} este paso oculta fácilmente la complejidad de la tarea. ^{[39] [40]}

Algoritmos cuánticos variacionales (VQA)

Los algoritmos cuánticos de calidad de datos (VQA) son uno de los algoritmos cuánticos más estudiados, ya que los investigadores esperan que todas las aplicaciones necesarias para la computadora cuántica utilicen los VQA y también los VQA parecen cumplir con la expectativa de obtener la supremacía cuántica. Los VQA son un enfoque cuántico-clásico mixto donde el procesador cuántico prepara los estados cuánticos y se realiza la medición y la optimización se realiza mediante una computadora clásica. Los VQA se consideran mejores para NISQ ya que los VQA son tolerantes al ruido en comparación con otros algoritmos y brindan superioridad cuántica con solo unos pocos cientos de qubits. Los investigadores han estudiado algoritmos basados ​​en circuitos para resolver problemas de optimización y encontrar la energía del estado fundamental de sistemas complejos, que eran difíciles de resolver o requerían mucho tiempo para realizar el cálculo utilizando una computadora clásica. ^{[41] [42]}

Circuitos cuánticos variacionales (CQV)

Los circuitos cuánticos variacionales, también conocidos como circuitos cuánticos parametrizados (PQC), se basan en algoritmos cuánticos variacionales (VQA). Los VQC constan de tres partes: preparación de estados iniciales, circuito cuántico y medición. Los investigadores están estudiando ampliamente los VQC, ya que utilizan el poder de la computación cuántica para aprender en poco tiempo y también utilizan menos parámetros que sus contrapartes clásicas. Está demostrado teórica y numéricamente que podemos aproximar funciones no lineales, como las que se utilizan en redes neuronales, en circuitos cuánticos. Debido a la superioridad de los VQC, la red neuronal ha sido reemplazada por VQC en tareas de aprendizaje por refuerzo y algoritmos generativos. La naturaleza intrínseca de los dispositivos cuánticos hacia la decoherencia, el error de compuerta aleatorio y los errores de medición hicieron que tuvieran un alto potencial para limitar el entrenamiento de los circuitos de variación. Entrenar los VQC en los dispositivos clásicos antes de emplearlos en dispositivos cuánticos ayuda a superar el problema del ruido de decoherencia que se produjo a través del número de repeticiones para el entrenamiento. ^{[43] [44] [45]}

Clasificador binario cuántico

La reorganización de patrones es una de las tareas importantes del aprendizaje automático, la clasificación binaria es una de las herramientas o algoritmos para encontrar patrones. La clasificación binaria se utiliza en el aprendizaje supervisado y en el aprendizaje no supervisado . En el aprendizaje automático cuántico, los bits clásicos se convierten en qubits y se asignan al espacio de Hilbert; los datos de valores complejos se utilizan en un clasificador binario cuántico para aprovechar las ventajas del espacio de Hilbert. ^{[46] [47]} Al explotar las propiedades de la mecánica cuántica, como la superposición, el entrelazamiento y la interferencia, el clasificador binario cuántico produce el resultado preciso en un corto período de tiempo. ^[48]

Algoritmos de aprendizaje automático cuántico basados ​​en la búsqueda de Grover

Otro enfoque para mejorar el aprendizaje automático clásico con procesamiento de información cuántica utiliza métodos de amplificación de amplitud basados ​​en el algoritmo de búsqueda de Grover , que ha demostrado resolver problemas de búsqueda no estructurada con una aceleración cuadrática en comparación con los algoritmos clásicos. Estas rutinas cuánticas se pueden emplear para algoritmos de aprendizaje que se traducen en una tarea de búsqueda no estructurada, como se puede hacer, por ejemplo, en el caso de los algoritmos de k-medianas ^[49] y de k-vecinos más cercanos ^[9] . Otras aplicaciones incluyen aceleraciones cuadráticas en el entrenamiento del perceptrón ^[50] y el cálculo de la atención ^[51] .

Un ejemplo de amplificación de amplitud que se utiliza en un algoritmo de aprendizaje automático es la minimización del algoritmo de búsqueda de Grover. En el que una subrutina utiliza el algoritmo de búsqueda de Grover para encontrar un elemento menor que algún elemento previamente definido. Esto se puede hacer con un oráculo que determina si un estado con un elemento correspondiente es menor que el predefinido. El algoritmo de Grover puede entonces encontrar un elemento tal que se cumpla nuestra condición. La minimización se inicializa con algún elemento aleatorio en nuestro conjunto de datos, y realiza iterativamente esta subrutina para encontrar el elemento mínimo en el conjunto de datos. Esta minimización se utiliza notablemente en k-medianas cuánticas, y tiene una velocidad de al menos en comparación con las versiones clásicas de k-medianas, donde es el número de puntos de datos y es el número de clústeres. ^[49] ${\displaystyle O({\sqrt {n/k}})}$ ${\displaystyle n}$ ${\displaystyle k}$

La amplificación de amplitud se combina a menudo con los recorridos cuánticos para lograr la misma aceleración cuadrática. Se ha propuesto que los recorridos cuánticos mejoran el algoritmo PageRank de Google ^[52], así como el rendimiento de los agentes de aprendizaje de refuerzo en el marco de simulación proyectiva. ^[53]

Aprendizaje de refuerzo mejorado cuánticamente

El aprendizaje por refuerzo es una rama del aprendizaje automático distinta del aprendizaje supervisado y no supervisado, que también admite mejoras cuánticas. ^{[54] [53] [55]} En el aprendizaje por refuerzo mejorado cuánticamente, un agente cuántico interactúa con un entorno clásico o cuántico y ocasionalmente recibe recompensas por sus acciones, lo que le permite adaptar su comportamiento, es decir, aprender qué hacer para obtener más recompensas. En algunas situaciones, ya sea por la capacidad de procesamiento cuántico del agente, ^[53] o por la posibilidad de sondear el entorno en superposiciones , ^[29] se puede lograr una aceleración cuántica. Se han propuesto implementaciones de este tipo de protocolos para sistemas de iones atrapados ^[56] y circuitos superconductores . ^[57] Se ha demostrado experimentalmente una aceleración cuántica del tiempo de toma de decisiones internas del agente ^{[53] en iones atrapados, [58]} mientras que se ha logrado experimentalmente una aceleración cuántica del tiempo de aprendizaje en una interacción totalmente coherente («cuántica») entre el agente y el entorno en una configuración fotónica. ^[59]

Recocido cuántico

El recocido cuántico es una técnica de optimización que se utiliza para determinar los mínimos y máximos locales de una función sobre un conjunto dado de funciones candidatas. Se trata de un método de discretización de una función con muchos mínimos o máximos locales para determinar los observables de la función. El proceso se puede distinguir del recocido simulado por el proceso de tunelización cuántica , mediante el cual las partículas atraviesan barreras cinéticas o potenciales desde un estado alto a un estado bajo. El recocido cuántico comienza con una superposición de todos los estados posibles de un sistema, ponderados de forma igual. A continuación, la ecuación de Schrödinger dependiente del tiempo guía la evolución temporal del sistema, lo que sirve para afectar la amplitud de cada estado a medida que aumenta el tiempo. Finalmente, se puede alcanzar el estado fundamental para obtener el hamiltoniano instantáneo del sistema.

Circuito NISQ como modelo cuántico

A medida que avanza la profundidad del circuito cuántico en los dispositivos NISQ , aumenta el nivel de ruido, lo que plantea un desafío significativo para calcular con precisión los costos y gradientes en los modelos de entrenamiento. La tolerancia al ruido se mejorará mediante el uso del perceptrón cuántico y el algoritmo cuántico en el hardware cuántico actualmente accesible. ^{[ cita requerida ]}

Una conexión regular de componentes similares, conocidos como neuronas, forma la base de incluso las redes cerebrales más complejas. Normalmente, una neurona tiene dos operaciones: el producto interno y una función de activación . A diferencia de la función de activación, que normalmente es no lineal , el producto interno es un proceso lineal. Con la computación cuántica, los procesos lineales se pueden llevar a cabo fácilmente; además, debido a la simplicidad de implementación, la mayoría de las neuronas cuánticas prefieren la función umbral para las funciones de activación. ^{[ cita requerida ]}

Técnicas de muestreo cuántico

El muestreo a partir de distribuciones de probabilidad de alta dimensión es el núcleo de un amplio espectro de técnicas computacionales con importantes aplicaciones en la ciencia, la ingeniería y la sociedad. Algunos ejemplos son el aprendizaje profundo , la programación probabilística y otras aplicaciones de aprendizaje automático e inteligencia artificial.

Un problema computacionalmente difícil, que es clave para algunas tareas relevantes de aprendizaje automático, es la estimación de promedios sobre modelos probabilísticos definidos en términos de una distribución de Boltzmann . El muestreo a partir de modelos probabilísticos genéricos es difícil: se espera que los algoritmos que dependen en gran medida del muestreo sigan siendo intratables sin importar cuán grandes y poderosos se vuelvan los recursos de computación clásica. Si bien los recocidos cuánticos, como los producidos por D-Wave Systems, fueron diseñados para problemas de optimización combinatoria desafiantes, recientemente se los ha reconocido como un candidato potencial para acelerar los cálculos que dependen del muestreo al explotar los efectos cuánticos. ^[60]

Algunos grupos de investigación han explorado recientemente el uso de hardware de recocido cuántico para entrenar máquinas de Boltzmann y redes neuronales profundas . ^{[61] [62] [63]} El enfoque estándar para entrenar máquinas de Boltzmann se basa en el cálculo de ciertos promedios que pueden estimarse mediante técnicas de muestreo estándar , como los algoritmos de Monte Carlo de cadena de Markov . Otra posibilidad es confiar en un proceso físico, como el recocido cuántico, que genera naturalmente muestras a partir de una distribución de Boltzmann. El objetivo es encontrar los parámetros de control óptimos que mejor representen la distribución empírica de un conjunto de datos dado.

El sistema D-Wave 2X alojado en el Centro de Investigación Ames de la NASA se ha utilizado recientemente para el aprendizaje de una clase especial de máquinas de Boltzmann restringidas que pueden servir como un bloque de construcción para arquitecturas de aprendizaje profundo. ^[62] Un trabajo complementario que apareció aproximadamente de manera simultánea mostró que el recocido cuántico se puede utilizar para el aprendizaje supervisado en tareas de clasificación. ^[61] El mismo dispositivo se utilizó más tarde para entrenar una máquina de Boltzmann completamente conectada para generar, reconstruir y clasificar dígitos escritos a mano de baja resolución y escala reducida, entre otros conjuntos de datos sintéticos. ^[64] En ambos casos, los modelos entrenados mediante recocido cuántico tuvieron un rendimiento similar o mejor en términos de calidad. La pregunta fundamental que impulsa este esfuerzo es si existe una aceleración cuántica en las aplicaciones de muestreo. La experiencia con el uso de recocidos cuánticos para la optimización combinatoria sugiere que la respuesta no es sencilla. El recocido inverso también se ha utilizado para resolver una máquina de Boltzmann restringida cuántica completamente conectada. ^[65]

Inspirado por el éxito de las máquinas de Boltzmann basadas en la distribución clásica de Boltzmann, recientemente se propuso un nuevo enfoque de aprendizaje automático basado en la distribución cuántica de Boltzmann de un hamiltoniano de Ising de campo transversal. ^[66] Debido a la naturaleza no conmutativa de la mecánica cuántica, el proceso de entrenamiento de la máquina cuántica de Boltzmann puede volverse no trivial. Este problema se eludió, hasta cierto punto, introduciendo límites en las probabilidades cuánticas, lo que permitió a los autores entrenar el modelo de manera eficiente mediante muestreo. Es posible que se haya entrenado un tipo específico de máquina cuántica de Boltzmann en D-Wave 2X utilizando una regla de aprendizaje análoga a la de las máquinas clásicas de Boltzmann. ^{[64] [63] [67]}

El recocido cuántico no es la única tecnología para el muestreo. En un escenario de preparación y medición, una computadora cuántica universal prepara un estado térmico, que luego se muestrea mediante mediciones. Esto puede reducir el tiempo requerido para entrenar una máquina de Boltzmann restringida profunda y proporcionar un marco más rico y completo para el aprendizaje profundo que la computación clásica. ^[68] Los mismos métodos cuánticos también permiten un entrenamiento eficiente de máquinas de Boltzmann completas y modelos multicapa completamente conectados y no tienen contrapartes clásicas bien conocidas. Basándose en un protocolo eficiente de preparación del estado térmico a partir de un estado arbitrario, las redes lógicas de Markov mejoradas cuánticamente explotan las simetrías y la estructura de localidad del modelo gráfico probabilístico generado por una plantilla lógica de primer orden . ^{[69] [19]} Esto proporciona una reducción exponencial en la complejidad computacional en la inferencia probabilística y, si bien el protocolo se basa en una computadora cuántica universal, bajo suposiciones moderadas se puede integrar en el hardware de recocido cuántico contemporáneo.

Redes neuronales cuánticas

Los análogos cuánticos o generalizaciones de las redes neuronales clásicas a menudo se denominan redes neuronales cuánticas . El término es reivindicado por una amplia gama de enfoques, incluida la implementación y extensión de redes neuronales que utilizan fotones, circuitos variacionales en capas o modelos cuánticos de tipo Ising. Las redes neuronales cuánticas a menudo se definen como una expansión del modelo de Deutsch de una red computacional cuántica. ^[70] Dentro de este modelo, se implementan puertas no lineales e irreversibles, diferentes al operador hamiltoniano, para especular el conjunto de datos dado. ^[70] Estas puertas hacen que ciertas fases no se puedan observar y generan oscilaciones específicas. ^[70] Las redes neuronales cuánticas aplican los principios de la información cuántica y la computación cuántica a la neurocomputación clásica. ^[71] La investigación actual muestra que QNN puede aumentar exponencialmente la cantidad de potencia de cálculo y los grados de libertad de una computadora, que está limitada para una computadora clásica a su tamaño. ^[71] Una red neuronal cuántica tiene capacidades computacionales para disminuir la cantidad de pasos, qubits utilizados y tiempo de cálculo. ^[70] La función de onda de la mecánica cuántica es la neurona de las redes neuronales. Para probar las aplicaciones cuánticas en una red neuronal, se depositan moléculas de puntos cuánticos sobre un sustrato de GaAs o similar para registrar cómo se comunican entre sí. Cada punto cuántico puede considerarse una isla de actividad eléctrica y, cuando dichos puntos están lo suficientemente cerca (aproximadamente entre 10 y 20 nm), ^[72] los electrones pueden hacer un túnel debajo de las islas. Una distribución uniforme a lo largo del sustrato en grupos de dos crea dipolos y, en última instancia, dos estados de espín, arriba o abajo. Estos estados se conocen comúnmente como qubits, con los estados correspondientes de y en la notación de Dirac. ^[72] ${\displaystyle |0\rangle }$ ${\displaystyle |1\rangle }$

Red neuronal de convolución cuántica

Un diseño novedoso para vectores multidimensionales que utiliza circuitos como filtros de convolución ^[73] es QCNN. Se inspiró en las ventajas de las CNN ^{[74] [75]} y la potencia de QML. Se realizó utilizando una combinación de un circuito cuántico variacional (VQC) ^[76] y una red neuronal profunda ^[77] (DNN), aprovechando al máximo el poder del procesamiento extremadamente paralelo en una superposición de un estado cuántico con un número finito de qubits. La estrategia principal es llevar a cabo un proceso de optimización iterativo en los dispositivos NISQ ^[78] , sin el impacto negativo del ruido, que posiblemente se incorpore al parámetro del circuito, y sin la necesidad de corrección de errores cuánticos. ^[79]

El circuito cuántico debe manejar de manera efectiva la información espacial para que la QCNN funcione como CNN. El filtro convolucional es la técnica más básica para hacer uso de la información espacial. Uno o más filtros convolucionales cuánticos conforman una red neuronal convolucional cuántica (QCNN), y cada uno de estos filtros transforma los datos de entrada utilizando un circuito cuántico que puede crearse de manera organizada o aleatoria. Tres partes que conforman el filtro convolucional cuántico son: el codificador, el circuito cuántico parametrizado (PQC), ^[80] y la medición. El filtro convolucional cuántico puede verse como una extensión del filtro en la CNN tradicional porque fue diseñado con parámetros entrenables.

Las redes neuronales cuánticas aprovechan las estructuras jerárquicas ^[81] y, para cada capa posterior, el número de qubits de la capa anterior se reduce en un factor de dos. Para n qubits de entrada, estas estructuras tienen capas O(log(n)), lo que permite una profundidad de circuito reducida. Además, pueden evitar la "meseta estéril", uno de los problemas más importantes de los algoritmos basados ​​en PQC, lo que garantiza la capacidad de entrenamiento ^[82] . A pesar de que el modelo QCNN no incluye la operación cuántica correspondiente, también se ofrece la idea fundamental de la capa de agrupación para asegurar la validez. En la arquitectura QCNN, la capa de agrupación se coloca normalmente entre capas convolucionales sucesivas. Su función es reducir el tamaño espacial de la representación al tiempo que se conservan las características cruciales, lo que le permite reducir el número de parámetros, agilizar la computación de la red y gestionar el sobreajuste. Dicho proceso se puede lograr aplicando una tomografía completa sobre el estado para reducirlo hasta un qubit y luego procesarlo en el metro. El tipo de unidad que se utiliza con más frecuencia en la capa de agrupamiento es el agrupamiento máximo, aunque también existen otros tipos. De manera similar a las redes neuronales de propagación hacia adelante convencionales , el último módulo es una capa completamente conectada con conexiones completas a todas las activaciones en la capa anterior. La invariancia traslacional, que requiere bloques idénticos de puertas cuánticas parametrizadas dentro de una capa, es una característica distintiva de la arquitectura QCNN. ^[83]

Red neuronal cuántica disipativa

Las QNN disipativas (DQNN) se construyen a partir de capas de qubits acoplados por perceptrones llamados bloques de construcción, que tienen un diseño unitario arbitrario. A cada nodo en la capa de red de una DQNN se le da una colección distinta de qubits, y a cada qubit también se le da un perceptrón cuántico único unitario para caracterizarlo. ^{[84] [85]} La información de los estados de entrada se transporta a través de la red en un modo de avance, mapeo de transición de capa a capa en los qubits de las dos capas adyacentes, como lo indica el nombre. El término disipativo también se refiere al hecho de que la capa de salida está formada por los qubits auxiliares mientras que las capas de entrada se descartan mientras se traza la capa final. ^[86] Al realizar una amplia tarea de aprendizaje supervisado, las DQNN se utilizan para aprender una matriz unitaria que conecta los estados cuánticos de entrada y salida. Los datos de entrenamiento para esta tarea consisten en el estado cuántico y las etiquetas clásicas correspondientes.

Inspirada en la extremadamente exitosa red generativa antagónica clásica (GAN) , ^[87] se introduce la red generativa antagónica cuántica disipativa (DQGAN) para el aprendizaje no supervisado de los datos de entrenamiento no etiquetados. El generador y el discriminador son las dos DQNN que forman una única DQGAN. ^[85] El objetivo del generador es crear estados de entrenamiento falsos que el discriminador no puede diferenciar de los genuinos, mientras que el objetivo del discriminador es separar los estados de entrenamiento reales de los estados falsos creados por el generador. Las características relevantes del conjunto de entrenamiento son aprendidas por el generador mediante el entrenamiento alternativo y antagónico de las redes que ayudan en la producción de conjuntos que extienden el conjunto de entrenamiento. DQGAN tiene una arquitectura completamente cuántica y está entrenada en datos cuánticos.

Modelos cuánticos ocultos de Markov

Los modelos cuánticos ocultos de Markov ^[88] (HQMM) son una versión mejorada cuánticamente de los modelos ocultos de Markov clásicos (HMM), que se utilizan normalmente para modelar datos secuenciales en varios campos como la robótica y el procesamiento del lenguaje natural . A diferencia del enfoque adoptado por otros algoritmos de aprendizaje automático mejorados cuánticamente, los HQMM pueden verse como modelos inspirados en la mecánica cuántica que también pueden ejecutarse en computadoras clásicas. ^[89] Mientras que los HMM clásicos utilizan vectores de probabilidad para representar estados de "creencia" ocultos, los HQMM utilizan el análogo cuántico: matrices de densidad . Trabajos recientes han demostrado que estos modelos se pueden aprender con éxito maximizando la verosimilitud logarítmica de los datos dados a través de la optimización clásica, y hay alguna evidencia empírica de que estos modelos pueden modelar mejor los datos secuenciales en comparación con los HMM clásicos en la práctica, aunque se necesita más trabajo para determinar exactamente cuándo y cómo se derivan estos beneficios. ^[89] Además, dado que los HMM clásicos son un tipo particular de red de Bayes , un aspecto interesante de los HQMM es que las técnicas utilizadas muestran cómo podemos realizar inferencia bayesiana análoga a la cuántica , lo que debería permitir la construcción general de las versiones cuánticas de modelos gráficos probabilísticos . ^[89]

Aprendizaje automático completamente cuántico

En el caso más general del aprendizaje automático cuántico, tanto el dispositivo de aprendizaje como el sistema en estudio, así como su interacción, son completamente cuánticos. En esta sección se ofrecen algunos ejemplos de resultados sobre este tema.

Una clase de problema que puede beneficiarse del enfoque completamente cuántico es el de "aprender" estados, procesos o mediciones cuánticas desconocidas, en el sentido de que uno puede reproducirlos posteriormente en otro sistema cuántico. Por ejemplo, uno puede desear aprender una medición que discrimine entre dos estados coherentes, dada no una descripción clásica de los estados a discriminar, sino en cambio un conjunto de sistemas cuánticos de ejemplo preparados en estos estados. El enfoque ingenuo sería extraer primero una descripción clásica de los estados y luego implementar una medición discriminante ideal basada en esta información. Esto solo requeriría aprendizaje clásico. Sin embargo, uno puede demostrar que un enfoque completamente cuántico es estrictamente superior en este caso. ^[90] (Esto también se relaciona con el trabajo sobre la coincidencia de patrones cuánticos. ^[91] ) El problema de aprender transformaciones unitarias se puede abordar de una manera similar. ^[92]

Más allá del problema específico de aprender estados y transformaciones, la tarea de agrupamiento también admite una versión completamente cuántica, en la que tanto el oráculo que devuelve la distancia entre los puntos de datos como el dispositivo de procesamiento de información que ejecuta el algoritmo son cuánticos. ^[93] Finalmente, en ^[29] se introdujo un marco general que abarca el aprendizaje supervisado, no supervisado y de refuerzo en el entorno completamente cuántico, donde también se demostró que la posibilidad de sondear el entorno en superposiciones permite una aceleración cuántica en el aprendizaje de refuerzo. Tal aceleración en el paradigma del aprendizaje de refuerzo se ha demostrado experimentalmente en una configuración fotónica. ^[59]

Aprendizaje automático cuántico explicable

La necesidad de modelos que puedan ser entendidos por humanos surge en el aprendizaje automático cuántico en analogía con el aprendizaje automático clásico e impulsa el campo de investigación del aprendizaje automático cuántico explicable (o XQML ^[94] en analogía con XAI/XML ). Estos esfuerzos a menudo también se conocen como aprendizaje automático interpretable (IML, y por extensión IQML). ^[95] XQML/IQML puede considerarse como una dirección de investigación alternativa en lugar de encontrar una ventaja cuántica. ^[96] Por ejemplo, XQML se ha utilizado en el contexto de la detección y clasificación de malware móvil. ^[97] También se han propuesto valores cuánticos de Shapley para interpretar puertas dentro de un circuito basado en un enfoque de teoría de juegos. ^[94] Para este propósito, las puertas en lugar de las características actúan como jugadores en un juego de coalición con una función de valor que depende de las mediciones del circuito cuántico de interés. Además, también se ha propuesto una versión cuántica de la técnica clásica conocida como LIME (Explicaciones agnósticas del modelo interpretable lineal) ^[98] , conocida como Q-LIME. ^[99]

Aprendizaje clásico aplicado a problemas cuánticos

El término "aprendizaje automático cuántico" a veces se refiere al aprendizaje automático clásico realizado sobre datos de sistemas cuánticos. Un ejemplo básico de esto es la tomografía de estados cuánticos , donde se aprende un estado cuántico a partir de mediciones. Otras aplicaciones incluyen el aprendizaje de hamiltonianos ^[100] y la generación automática de experimentos cuánticos. ^[20]

Teoría del aprendizaje cuántico

La teoría del aprendizaje cuántico persigue un análisis matemático de las generalizaciones cuánticas de los modelos de aprendizaje clásicos y de las posibles aceleraciones u otras mejoras que pueden proporcionar. El marco es muy similar al de la teoría clásica del aprendizaje computacional , pero el alumno en este caso es un dispositivo de procesamiento de información cuántica, mientras que los datos pueden ser clásicos o cuánticos. La teoría del aprendizaje cuántico debe contrastarse con el aprendizaje automático mejorado cuánticamente discutido anteriormente, donde el objetivo era considerar problemas específicos y utilizar protocolos cuánticos para mejorar la complejidad temporal de los algoritmos clásicos para estos problemas. Aunque la teoría del aprendizaje cuántico aún está en desarrollo, se han obtenido resultados parciales en esta dirección. ^[101]

El punto de partida de la teoría del aprendizaje suele ser una clase de conceptos, un conjunto de conceptos posibles. Normalmente, un concepto es una función de algún dominio, como . Por ejemplo, la clase de conceptos podría ser el conjunto de fórmulas de forma normal disyuntiva (DNF) en n bits o el conjunto de circuitos booleanos de cierta profundidad constante. El objetivo del alumno es aprender (de forma exacta o aproximada) un concepto objetivo desconocido de esta clase de conceptos. El alumno puede estar interactuando activamente con el concepto objetivo o recibiendo muestras pasivas de él. ${\displaystyle \{0,1\}^{n}}$

En el aprendizaje activo, un alumno puede realizar consultas de pertenencia al concepto objetivo c, preguntando por su valor c(x) en las entradas x elegidas por el alumno. El alumno luego tiene que reconstruir el concepto objetivo exacto, con alta probabilidad. En el modelo de aprendizaje cuántico exacto, el alumno puede realizar consultas de pertenencia en superposición cuántica. Si la complejidad del alumno se mide por la cantidad de consultas de pertenencia que realiza, entonces los alumnos cuánticos exactos pueden ser polinómicamente más eficientes que los alumnos clásicos para algunas clases de conceptos, pero no más. ^[102] Si la complejidad se mide por la cantidad de tiempo que utiliza el alumno, entonces hay clases de conceptos que pueden ser aprendidas eficientemente por los alumnos cuánticos pero no por los alumnos clásicos (bajo supuestos plausibles de teoría de la complejidad). ^[102]

Un modelo natural de aprendizaje pasivo es el aprendizaje probablemente aproximadamente correcto (PAC) de Valiant . Aquí el alumno recibe ejemplos aleatorios (x, c(x)), donde x se distribuye según alguna distribución desconocida D. El objetivo del alumno es generar una función de hipótesis h tal que h(x)=c(x) con alta probabilidad cuando x se extrae según D. El alumno tiene que ser capaz de producir dicha h "aproximadamente correcta" para cada D y cada concepto objetivo c en su clase de concepto. Podemos considerar reemplazar los ejemplos aleatorios por ejemplos cuánticos potencialmente más poderosos . En el modelo PAC (y el modelo agnóstico relacionado), esto no reduce significativamente el número de ejemplos necesarios: para cada clase de concepto, la complejidad de la muestra clásica y cuántica son las mismas hasta factores constantes. ^[103] Sin embargo, para aprender bajo alguna distribución fija D, los ejemplos cuánticos pueden ser muy útiles, por ejemplo para aprender DNF bajo la distribución uniforme. ^[104] Al considerar la complejidad temporal, existen clases de conceptos que pueden ser aprendidas mediante PAC de manera eficiente por aprendices cuánticos, incluso a partir de ejemplos clásicos, pero no por aprendices clásicos (de nuevo, bajo supuestos plausibles de teoría de la complejidad). ^[102] ${\displaystyle \sum _{x}{\sqrt {D(x)}}|x,c(x)\rangle }$

Este tipo de aprendizaje pasivo es también el esquema más común en el aprendizaje supervisado: un algoritmo de aprendizaje normalmente toma los ejemplos de entrenamiento fijos, sin la capacidad de consultar la etiqueta de los ejemplos no etiquetados. Generar una hipótesis h es un paso de inducción. Clásicamente, un modelo inductivo se divide en una fase de entrenamiento y una fase de aplicación: los parámetros del modelo se estiman en la fase de entrenamiento y el modelo aprendido se aplica un número arbitrario de veces en la fase de aplicación. En el límite asintótico del número de aplicaciones, esta división de fases también está presente con los recursos cuánticos. ^[105]

Implementaciones y experimentos

Los primeros experimentos se llevaron a cabo utilizando la computadora cuántica adiabática D-Wave , por ejemplo, para detectar automóviles en imágenes digitales utilizando un impulso regularizado con una función objetivo no convexa en una demostración en 2009. ^[106] Muchos experimentos siguieron con la misma arquitectura, y las principales empresas tecnológicas han mostrado interés en el potencial del aprendizaje automático cuántico para futuras implementaciones tecnológicas. En 2013, Google Research, la NASA y la Asociación de Investigación Espacial de Universidades lanzaron el Laboratorio de Inteligencia Artificial Cuántica que explora el uso de la computadora cuántica adiabática D-Wave. ^{[107] [108]} Un ejemplo más reciente entrenó modelos generativos probabilísticos con conectividad por pares arbitraria, mostrando que su modelo es capaz de generar dígitos escritos a mano, así como reconstruir imágenes ruidosas de barras y rayas y dígitos escritos a mano. ^[64]

Utilizando una tecnología de recocido diferente basada en resonancia magnética nuclear (RMN), se implementó una red de Hopfield cuántica en 2009 que mapeó los datos de entrada y los datos memorizados a hamiltonianos, lo que permitió el uso de computación cuántica adiabática. ^[109] La tecnología de RMN también permite la computación cuántica universal, ^{[ cita requerida ]} y se utilizó para la primera implementación experimental de una máquina de vectores de soporte cuántico para distinguir los números escritos a mano "6" y "9" en una computadora cuántica de estado líquido en 2015. ^[110] Los datos de entrenamiento involucraron el preprocesamiento de la imagen que los mapea a vectores bidimensionales normalizados para representar las imágenes como los estados de un qubit. Las dos entradas del vector son la relación vertical y horizontal de la intensidad del píxel de la imagen. Una vez que los vectores se definen en el espacio de características , se implementó la máquina de vectores de soporte cuántico para clasificar el vector de entrada desconocido. La lectura evita la costosa tomografía cuántica al leer el estado final en términos de dirección (arriba/abajo) de la señal de RMN.

Las implementaciones fotónicas están atrayendo más atención, ^[111] en parte porque no requieren un enfriamiento extenso. En 2013, se demostró el reconocimiento simultáneo de dígitos y hablantes y la predicción caótica de series temporales a velocidades de datos superiores a 1 gigabyte por segundo. ^[112] Al utilizar fotónica no lineal para implementar un clasificador lineal totalmente óptico, un modelo de perceptrón fue capaz de aprender el límite de clasificación de manera iterativa a partir de datos de entrenamiento mediante una regla de retroalimentación. ^[113] Un componente básico de muchos algoritmos de aprendizaje es calcular la distancia entre dos vectores: esto se demostró experimentalmente por primera vez para hasta ocho dimensiones utilizando qubits entrelazados en una computadora cuántica fotónica en 2015. ^[114]

Recientemente, basándose en un enfoque neuromimético, se ha añadido un ingrediente novedoso al campo del aprendizaje automático cuántico, en forma de un llamado memristor cuántico, un modelo cuantizado del memristor clásico estándar . ^[115] Este dispositivo se puede construir por medio de una resistencia sintonizable, mediciones débiles en el sistema y un mecanismo clásico de retroalimentación. Se ha propuesto una implementación de un memristor cuántico en circuitos superconductores, ^[116] y se ha realizado un experimento con puntos cuánticos. ^[117] Un memristor cuántico implementaría interacciones no lineales en la dinámica cuántica que ayudarían a la búsqueda de una red neuronal cuántica completamente funcional.

Desde 2016, IBM ha lanzado una plataforma en línea basada en la nube para desarrolladores de software cuántico, llamada IBM Q Experience . Esta plataforma consta de varios procesadores cuánticos completamente operativos a los que se puede acceder a través de la API web de IBM. De esta manera, la empresa está alentando a los desarrolladores de software a buscar nuevos algoritmos a través de un entorno de desarrollo con capacidades cuánticas. Se están explorando nuevas arquitecturas de forma experimental, de hasta 32 cúbits, utilizando métodos de computación cuántica de iones atrapados y superconductores.

En octubre de 2019, se observó que la introducción de generadores de números aleatorios cuánticos (QRNG) a los modelos de aprendizaje automático, incluidas las redes neuronales y las redes neuronales convolucionales para la distribución de peso inicial aleatorio y los bosques aleatorios para los procesos de división, tuvieron un efecto profundo en su capacidad en comparación con el método clásico de generadores de números pseudoaleatorios (PRNG). ^[118] Sin embargo, en una publicación más reciente de 2021, estas afirmaciones no se pudieron reproducir para la inicialización del peso de la red neuronal y no se encontró ninguna ventaja significativa de usar QRNG sobre PRNG. ^[119] El trabajo también demostró que la generación de números aleatorios justos con una computadora cuántica de puerta es una tarea no trivial en dispositivos NISQ y, por lo tanto, los QRNG suelen ser mucho más difíciles de usar en la práctica que los PRNG.

Un artículo publicado en diciembre de 2018 informó sobre un experimento que utilizó un sistema de iones atrapados que demostró una aceleración cuántica del tiempo de deliberación de los agentes de aprendizaje de refuerzo que emplean hardware cuántico interno. ^[58]

En marzo de 2021, un equipo de investigadores de Austria, Países Bajos, EE. UU. y Alemania informaron sobre la demostración experimental de una aceleración cuántica del tiempo de aprendizaje de los agentes de aprendizaje de refuerzo que interactúan de forma totalmente cuántica con el entorno. ^{[120] [59]} Los grados de libertad relevantes tanto del agente como del entorno se realizaron en un procesador nanofotónico integrado compacto y totalmente ajustable.

Escepticismo

Si bien el aprendizaje automático en sí mismo no es solo un campo de investigación, sino una industria económicamente significativa y de rápido crecimiento, y la computación cuántica es un campo bien establecido de investigación tanto teórica como experimental, el aprendizaje automático cuántico sigue siendo un campo de estudio puramente teórico. Los intentos de demostrar experimentalmente los conceptos del aprendizaje automático cuántico siguen siendo insuficientes. ^{[ cita requerida ]}

Muchos de los científicos líderes que publican extensamente en el campo del aprendizaje automático cuántico advierten sobre el gran revuelo en torno al tema y son muy comedidos cuando se les pregunta sobre sus usos prácticos en el futuro previsible. Sophia Chen ^[121] recopiló algunas de las declaraciones realizadas por científicos conocidos en el campo:

• "Creo que todavía no hemos hecho los deberes. Se trata de un campo científico muy nuevo", afirma la física Maria Schuld, de la startup canadiense de computación cuántica Xanadu.
• “Al mezclar el aprendizaje automático con la computación cuántica, se cataliza un condensado de propaganda”. ^[122] - Jacob Biamonte, colaborador de la teoría de la computación cuántica.
• "Hay mucho más trabajo por hacer antes de afirmar que el aprendizaje automático cuántico realmente funcionará", afirma el informático Iordanis Kerenidis, director de algoritmos cuánticos en QC Ware, una startup de computación cuántica con sede en Silicon Valley.
• "No he visto una sola prueba de que exista una tarea significativa [de aprendizaje automático] para la que tendría sentido utilizar un ordenador cuántico y no un ordenador clásico", afirma el físico Ryan Sweke de la Universidad Libre de Berlín, en Alemania.
• “¡No se dejen llevar por la propaganda!” – Frank Zickert, autor de probablemente el libro más práctico relacionado con el tema, tenga cuidado: “los ordenadores cuánticos están muy lejos de hacer avanzar el aprendizaje automático en cuanto a su capacidad de representación”, e incluso hablando de evaluación y optimización para cualquier tipo de tarea útil, la supremacía cuántica aún no se ha alcanzado. Además, ninguno de los investigadores activos en el campo hace ningún pronóstico sobre cuándo podría volverse práctico. ^{[ cita requerida ]}

Véase también

• Programación diferenciable
• Computación cuántica
• Algoritmo cuántico para sistemas lineales de ecuaciones
• Recocido cuántico
• Red neuronal cuántica
• Imagen cuántica

Referencias

1. Ventura, Dan (2000). "Memoria asociativa cuántica". Ciencias de la información . 124 (1–4): 273–296. arXiv : quant-ph/9807053 . doi :10.1016/S0020-0255(99)00101-2. S2CID  7232952.
2. Trugenberger, Carlo A. (2001). "Memorias cuánticas probabilísticas". Physical Review Letters . 87 (6): 067901. arXiv : quant-ph/0012100 . Código Bibliográfico :2001PhRvL..87f7901T. doi :10.1103/PhysRevLett.87.067901. PMID  11497863. S2CID  23325931.
3. Trugenberger, Carlo A. (2002). "Reconocimiento de patrones cuánticos". Procesamiento de información cuántica . 1 (6): 471–493. arXiv : quant-ph/0210176 . Código Bib : 2002QuiP....1..471T. doi :10.1023/A:1024022632303. S2CID  1928001.
4. Trugenberger, CA (19 de diciembre de 2002). "Transiciones de fase en el reconocimiento de patrones cuánticos". Physical Review Letters . 89 (27): 277903. arXiv : quant-ph/0204115 . Código Bibliográfico :2002PhRvL..89A7903T. doi :10.1103/physrevlett.89.277903. ISSN  0031-9007. PMID  12513243. S2CID  33065081.
5. Biamonte, Jacob; Wittek, Peter; Nicola, Pancotti; Rebentrost, Patrick; Wiebe, Nathan; Lloyd, Seth (2017). "Aprendizaje automático cuántico". Nature . 549 (7671): 195–202. arXiv : 1611.09347 . Código Bibliográfico :2017Natur.549..195B. doi :10.1038/nature23474. PMID  28905917. S2CID  64536201.
6. Schuld, Maria; Petruccione, Francesco (2018). Aprendizaje supervisado con computadoras cuánticas . Ciencia y tecnología cuánticas. Bibcode :2018slqc.book.....S. doi :10.1007/978-3-319-96424-9. ISBN 978-3-319-96423-2.
7. Schuld, Maria; Sinayskiy, Ilya; Petruccione, Francesco (2014). "Una introducción al aprendizaje automático cuántico". Física contemporánea . 56 (2): 172–185. arXiv : 1409.3097 . Código Bibliográfico :2015ConPh..56..172S. CiteSeerX 10.1.1.740.5622 . doi :10.1080/00107514.2014.964942. S2CID  119263556. 
8. Wittek, Peter (2014). Aprendizaje automático cuántico: qué significa la computación cuántica para la minería de datos. Academic Press. ISBN 978-0-12-800953-6.
9. Wiebe, Nathan; Kapoor, Ashish; Svore, Krysta (2014). "Algoritmos cuánticos para métodos de vecino más cercano para aprendizaje supervisado y no supervisado". Información y computación cuántica . 15 (3): 0318–0358. arXiv : 1401.2142 .
10. Lloyd, Seth; Mohseni, Masoud; Rebentrost, Patrick (2013). "Algoritmos cuánticos para aprendizaje automático supervisado y no supervisado". arXiv : 1307.0411 [quant-ph].
11. Yoo, Seokwon; Bang, Jeongho; Lee, Changhyoup; Lee, Jinhyoung (2014). "Una aceleración cuántica en el aprendizaje automático: Encontrar una función booleana de N bits para una clasificación". New Journal of Physics . 16 (10): 103014. arXiv : 1303.6055 . Bibcode :2014NJPh...16j3014Y. doi :10.1088/1367-2630/16/10/103014. S2CID  4956424.
12. Schuld, Maria; Sinayskiy, Ilya; Petruccione, Francesco (15 de octubre de 2014). "Una introducción al aprendizaje automático cuántico". Física contemporánea . 56 (2): 172–185. arXiv : 1409.3097 . Código Bibliográfico :2015ConPh..56..172S. CiteSeerX 10.1.1.740.5622 . doi :10.1080/00107514.2014.964942. ISSN  0010-7514. S2CID  119263556. 
13. Benedetti, Marcello; Realpe-Gómez, John; Biswas, Rupak; Perdomo-Ortiz, Alejandro (30 de noviembre de 2017). "Aprendizaje asistido por cuántica de modelos gráficos probabilísticos embebidos en hardware". Physical Review X . 7 (4): 041052. arXiv : 1609.02542 . Código Bibliográfico :2017PhRvX...7d1052B. doi :10.1103/PhysRevX.7.041052. ISSN  2160-3308. S2CID  55331519.
14. Farhi, Edward; Neven, Hartmut (16 de febrero de 2018). "Clasificación con redes neuronales cuánticas en procesadores de corto plazo". arXiv : 1802.06002 [quant-ph].
15. Schuld, Maria; Bocharov, Alex; Svore, Krysta ; Wiebe, Nathan (2020). "Clasificadores cuánticos centrados en circuitos". Physical Review A . 101 (3): 032308. arXiv : 1804.00633 . Código Bibliográfico :2020PhRvA.101c2308S. doi :10.1103/PhysRevA.101.032308. S2CID  49577148.
16. Yu, Shang; Albarrán-Arriagada, F.; Retamal, JC; Wang, Yi-Tao; Liu, Wei; Ke, Zhi-Jin; Meng, Yu; Li, Zhi-Peng; Tang, Jian-Shun (28 de agosto de 2018). "Reconstrucción de un estado de Qubit fotónico con aprendizaje por refuerzo cuántico". Tecnologías cuánticas avanzadas . 2 (7–8): 1800074. arXiv : 1808.09241 . doi :10.1002/qute.201800074. S2CID  85529734.
17. Ghosh, Sanjib; Opala, A.; Matuszewski, M.; Paterek, T.; Liew, Timothy CH (2019). "Procesamiento cuántico de yacimientos". npj Quantum Information . 5 (35): 35. arXiv : 1811.10335 . Código Bibliográfico :2019npjQI...5...35G. doi :10.1038/s41534-019-0149-8. S2CID  119197635.
18. Broecker, Peter; Assaad, Fakher F.; Trebst, Simon (3 de julio de 2017). "Reconocimiento de fase cuántica mediante aprendizaje automático no supervisado". arXiv : 1707.00663 [cond-mat.str-el].
19. Huembeli, Patrick; Dauphin, Alexandre; Wittek, Peter (2018). "Identificación de transiciones de fase cuántica con redes neuronales adversarias". Physical Review B . 97 (13): 134109. arXiv : 1710.08382 . Código Bibliográfico :2018PhRvB..97m4109H. doi :10.1103/PhysRevB.97.134109. ISSN  2469-9950. S2CID  125593239.
20. Krenn, Mario (1 de enero de 2016). "Búsqueda automatizada de nuevos experimentos cuánticos". Physical Review Letters . 116 (9): 090405. arXiv : 1509.02749 . Código Bibliográfico :2016PhRvL.116i0405K. doi :10.1103/PhysRevLett.116.090405. PMID  26991161. S2CID  20182586.
21. Knott, Paul (22 de marzo de 2016). "Un algoritmo de búsqueda para la ingeniería de estados cuánticos y la metrología". New Journal of Physics . 18 (7): 073033. arXiv : 1511.05327 . Bibcode :2016NJPh...18g3033K. doi :10.1088/1367-2630/18/7/073033. S2CID  2721958.
22. Dunjko, Vedran; Briegel, Hans J (19 de junio de 2018). "Aprendizaje automático e inteligencia artificial en el dominio cuántico: una revisión del progreso reciente". Informes sobre el progreso en física . 81 (7): 074001. arXiv : 1709.02779 . Bibcode :2018RPPh...81g4001D. doi :10.1088/1361-6633/aab406. hdl : 1887/71084 . ISSN  0034-4885. PMID  29504942. S2CID  3681629.
23. Huggins, William; Patel, Piyush; Whaley, K. Birgitta; Stoudenmire, E. Miles (30 de marzo de 2018). "Hacia el aprendizaje automático cuántico con redes tensoriales". Ciencia y tecnología cuántica . 4 (2): 024001. arXiv : 1803.11537 . doi :10.1088/2058-9565/aaea94. S2CID  4531946.
24. Carleo, Giuseppe; Nomura, Yusuke; Imada, Masatoshi (26 de febrero de 2018). "Construcción de representaciones exactas de sistemas cuánticos de muchos cuerpos con redes neuronales profundas". Nature Communications . 9 (1): 5322. arXiv : 1802.09558 . Bibcode :2018NatCo...9.5322C. doi :10.1038/s41467-018-07520-3. PMC 6294148 . PMID  30552316. 
25. Bény, Cédric (14 de enero de 2013). "Aprendizaje profundo y el grupo de renormalización". arXiv : 1301.3124 [quant-ph].
26. Arunachalam, Srinivasan; de Wolf, Ronald (24 de enero de 2017). "Un estudio de la teoría del aprendizaje cuántico". arXiv : 1701.06806 [quant-ph].
27. Sergioli, Giuseppe; Giuntini, Roberto; Freytes, Hector (9 de mayo de 2019). "Un nuevo enfoque cuántico para la clasificación binaria". PLOS ONE . ​​14 (5): e0216224. Bibcode :2019PLoSO..1416224S. doi : 10.1371/journal.pone.0216224 . PMC 6508868 . PMID  31071129. 
28. Aïmeur, Esma; Brassard, Gilles; Gambs, Sébastien (7 de junio de 2006). "Aprendizaje automático en un mundo cuántico". Avances en inteligencia artificial . Apuntes de clase en informática. Vol. 4013. págs. 431–442. doi :10.1007/11766247_37. ISBN 978-3-540-34628-9.
29. Dunjko, Vedran; Taylor, Jacob M.; Briegel, Hans J. (20 de septiembre de 2016). "Aprendizaje automático mejorado cuánticamente". Physical Review Letters . 117 (13): 130501. arXiv : 1610.08251 . Código Bibliográfico :2016PhRvL.117m0501D. doi :10.1103/PhysRevLett.117.130501. PMID  27715099. S2CID  12698722.
30. Rebentrost, Patrick; Mohseni, Masoud; Lloyd, Seth (2014). "Máquina de vectores de soporte cuántico para la clasificación de macrodatos". Physical Review Letters . 113 (13): 130503. arXiv : 1307.0471 . Código Bibliográfico :2014PhRvL.113m0503R. doi :10.1103/PhysRevLett.113.130503. hdl :1721.1/90391. PMID  25302877. S2CID  5503025.
31. Wiebe, Nathan; Braun, Daniel; Lloyd, Seth (2012). "Algoritmo cuántico para ajuste de datos". Physical Review Letters . 109 (5): 050505. arXiv : 1204.5242 . Código Bibliográfico :2012PhRvL.109e0505W. doi :10.1103/PhysRevLett.109.050505. PMID  23006156. S2CID  118439810.
32. Schuld, Maria; Sinayskiy, Ilya; Petruccione, Francesco (2016). "Predicción por regresión lineal en una computadora cuántica". Physical Review A . 94 (2): 022342. arXiv : 1601.07823 . Código Bibliográfico :2016PhRvA..94b2342S. doi :10.1103/PhysRevA.94.022342. S2CID  118459345.
33. Harrow, Aram W.; Hassidim, Avinatan; Lloyd, Seth (2008). "Algoritmo cuántico para resolver sistemas lineales de ecuaciones". Physical Review Letters . 103 (15): 150502. arXiv : 0811.3171 . Código Bibliográfico :2009PhRvL.103o0502H. doi :10.1103/PhysRevLett.103.150502. PMID  19905613. S2CID  5187993.
34. Berry, Dominic W.; Childs, Andrew M.; Kothari, Robin (2015). "Simulación hamiltoniana con dependencia casi óptima de todos los parámetros". 2015 IEEE 56th Annual Symposium on Foundations of Computer Science . 56th Annual Symposium on Foundations of Computer Science. IEEE. págs. 792–809. arXiv : 1501.01715 . doi :10.1109/FOCS.2015.54. ISBN . 978-1-4673-8191-8.
35. Lloyd, Seth; Mohseni, Masoud; Rebentrost, Patrick (2014). "Análisis cuántico de componentes principales". Nature Physics . 10 (9): 631. arXiv : 1307.0401 . Código Bibliográfico :2014NatPh..10..631L. CiteSeerX 10.1.1.746.480 . doi :10.1038/nphys3029. S2CID  11553314. 
36. Zhao, Zhikuan; Fitzsimons, Jack K.; Fitzsimons, Joseph F. (2019). "Regresión de proceso gaussiano asistido cuánticamente". Physical Review A . 99 (5): 052331. arXiv : 1512.03929 . Código Bibliográfico :2019PhRvA..99e2331Z. doi :10.1103/PhysRevA.99.052331. S2CID  18303333.
37. Soklakov, Andrei N.; Schack, Rüdiger (2006). "Preparación eficiente de estados para un registro de bits cuánticos". Physical Review A . 73 (1): 012307. arXiv : quant-ph/0408045 . Código Bibliográfico :2006PhRvA..73a2307S. doi :10.1103/PhysRevA.73.012307. S2CID  17318769.
38. Giovannetti, Vittorio; Lloyd, Seth; MacCone, Lorenzo (2008). "Memoria de acceso aleatorio cuántico". Physical Review Letters . 100 (16): 160501. arXiv : 0708.1879 . Código Bibliográfico :2008PhRvL.100p0501G. doi :10.1103/PhysRevLett.100.160501. PMID  18518173. S2CID  570390.
39. Aaronson, Scott (2015). "Lea la letra pequeña". Nature Physics . 11 (4): 291–293. Código Bibliográfico :2015NatPh..11..291A. doi :10.1038/nphys3272. S2CID  122167250.
40. Bang, Jeongho; Dutta, Arijit; Lee, Seung-Woo; Kim, Jaewan (2019). "Uso óptimo de la memoria de acceso aleatorio cuántico en el aprendizaje automático cuántico". Physical Review A . 99 (1): 012326. arXiv : 1809.04814 . Código Bibliográfico :2019PhRvA..99a2326B. doi :10.1103/PhysRevA.99.012326. S2CID  62841090.
41. "Computación cuántica: el gran futuro de las finanzas en 2024" . Consultado el 17 de junio de 2023 .
42. "Computación clásica vs. computación cuántica". GeeksforGeeks . 2019-06-12 . Consultado el 2023-06-17 .
43. Peddireddy, Dheeraj; Bansal, V.; Jacob, Z.; Aggarwal, V. (2022). "Circuitos cuánticos variacionales parametrizados con anillo tensor para aprendizaje automático cuántico a gran escala". arXiv : 2201.08878 [quant-ph].
44. Griol-Barres, Israel; Milla, Sergio; Cebrián, Antonio; Mansoori, Yashar; Millet, José (enero de 2021). "Circuitos cuánticos variacionales para aprendizaje automático. Una aplicación para la detección de señales débiles". Applied Sciences . 11 (14): 6427. doi : 10.3390/app11146427 . hdl : 10251/182654 . ISSN  2076-3417.
45. Chen, Samuel Yen-Chi; Yang, Chao-Han Huck; Qi, Jun; Chen, Pin-Yu; Ma, Xiaoli; Goan, Hsi-Sheng (2020). "Circuitos cuánticos variacionales para aprendizaje de refuerzo profundo". IEEE Access . 8 : 141007–141024. arXiv : 1907.00397 . Bibcode :2020IEEEA...8n1007C. doi :10.1109/ACCESS.2020.3010470. ISSN  2169-3536. S2CID  195767325.
46. Park, Daniel K.; Blank, Carsten; Petruccione, Francesco (27 de julio de 2020). "La teoría del clasificador binario cuántico basado en núcleo". Physics Letters A . 384 (21): 126422. arXiv : 2004.03489 . Bibcode :2020PhLA..38426422P. doi :10.1016/j.physleta.2020.126422. ISSN  0375-9601. S2CID  215238793.
47. Yi, Teng; Wang, Jie; Xu, Fufang (1 de agosto de 2021). "Clasificación binaria de cúbits individuales utilizando el método de aprendizaje automático cuántico". Journal of Physics: Conference Series . 2006 (1): 012020. doi : 10.1088/1742-6596/2006/1/012020 . ISSN  1742-6588. S2CID  237286847.
48. Maheshwari, Danyal; Sierra-Sosa, Daniel; Garcia-Zapirain, Begonya (2022). "Clasificador cuántico variacional para clasificación binaria: conjunto de datos reales frente a sintéticos". IEEE Access . 10 : 3705–3715. Bibcode :2022IEEEA..10.3705M. doi : 10.1109/ACCESS.2021.3139323 . ISSN  2169-3536. S2CID  245614428.
49. Aïmeur, Esma; Brassard, Gilles; Gambs, Sébastien (1 de febrero de 2013). "Aceleración cuántica para el aprendizaje no supervisado". Aprendizaje automático . 90 (2): 261–287. doi : 10.1007/s10994-012-5316-5 . ISSN  0885-6125.
50. Wiebe, Nathan; Kapoor, Ashish; Svore, Krysta M. (2016). Modelos de perceptrones cuánticos. Avances en sistemas de procesamiento de información neuronal. Vol. 29. págs. 3999–4007. arXiv : 1602.04799 .
51. Gao, Yeqi (16 de julio de 2023). "Algoritmo cuántico rápido para el cálculo de la atención". arXiv : 2307.08045 [quant-ph].
52. Paparo, Giuseppe Davide; Martin-Delgado, Miguel Angel (2012). "Google en una red cuántica". Scientific Reports . 2 (444): 444. arXiv : 1112.2079 . Bibcode :2012NatSR...2E.444P. doi :10.1038/srep00444. PMC 3370332 . PMID  22685626. 
53. Paparo, Giuseppe Davide; Dunjko, Vedran; Makmal, Adi; Martin-Delgado, Miguel Angel; Briegel, Hans J. (2014). "Aceleración cuántica para agentes de aprendizaje activo". Physical Review X . 4 (3): 031002. arXiv : 1401.4997 . Código Bibliográfico :2014PhRvX...4c1002P. doi :10.1103/PhysRevX.4.031002. S2CID  54652978.
54. Dong, Daoyi; Chen, Chunlin; Li, Hanxiong; Tarn, Tzyh-Jong (2008). "Aprendizaje por refuerzo cuántico". IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics . 38 (5): 1207–1220. arXiv : 0810.3828 . CiteSeerX 10.1.1.243.5369 . doi :10.1109/TSMCB.2008.925743. PMID  18784007. S2CID  17768796. 
55. Crawford, Daniel; Levit, Anna; Ghadermarzy, Navid; Oberoi, Jaspreet S.; Ronagh, Pooya (2018). "Aprendizaje por refuerzo utilizando máquinas Quantum Boltzmann". arXiv : 1612.05695 [cuántico-ph].
56. Dunjko, Vedran; Friis, Nicolai; Briegel, Hans J. (1 de enero de 2015). "Deliberación mejorada cuánticamente de agentes de aprendizaje que utilizan iones atrapados". New Journal of Physics . 17 (2): 023006. arXiv : 1407.2830 . Bibcode :2015NJPh...17b3006D. doi :10.1088/1367-2630/17/2/023006. ISSN  1367-2630. S2CID  119292539.
57. Lamata, Lucas (2017). "Protocolos básicos en aprendizaje por refuerzo cuántico con circuitos superconductores". Scientific Reports . 7 (1): 1609. arXiv : 1701.05131 . Bibcode :2017NatSR...7.1609L. doi :10.1038/s41598-017-01711-6. PMC 5431677 . PMID  28487535. 
58. Sriarunothai, Theeraphot; Wölk, Sabine; Giri, Gouri Shankar; Friis, Nicolai; Dunjko, Vedran; Briegel, Hans J.; Wunderlich, Christof (2019). "Acelerar la toma de decisiones de un agente de aprendizaje mediante un procesador cuántico de trampa de iones". Ciencia y tecnología cuánticas . 4 (1): 015014. arXiv : 1709.01366 . Código Bib : 2019QS&T....4a5014S. doi :10.1088/2058-9565/aaef5e. ISSN  2058-9565. S2CID  2429346.
59. Saggio, Valeria; Asenbeck, Beate; Hamann, Arne; Strömberg, Teodor; Schiansky, Peter; Dunjko, Vedran; Friis, Nicolai; Harris, Nicolás C.; Hochberg, Michael; Englund, Dirk; Wölk, Sabine; Briegel, Hans J.; Walther, Philip (10 de marzo de 2021). "Aceleración cuántica experimental en agentes de aprendizaje por refuerzo". Naturaleza . 591 (7849): 229–233. arXiv : 2103.06294 . Código Bib :2021Natur.591..229S. doi :10.1038/s41586-021-03242-7. ISSN  1476-4687. PMC 7612051 . Número de modelo: PMID  33692560. Número de modelo: S2CID  232185235. 
60. Biswas, Rupak ; Jiang, Zhang; Kechezi, Kostya; Knysh, Sergey; Mandrá, Salvatore; O'Gorman, Bryan; Perdomo-Ortiz, Alejando; Pethukov, André; Realpe-Gómez, John; Rieffel, Eleanor; Venturelli, Davide; Vasko, Fedir; Wang, Zhihui (2016). "Una perspectiva de la NASA sobre la computación cuántica: oportunidades y desafíos". Computación Paralela . 64 : 81–98. arXiv : 1704.04836 . doi :10.1016/j.parco.2016.11.002. S2CID  27547901.
61. Adachi, Steven H.; Henderson, Maxwell P. (2015). "Aplicación del recocido cuántico al entrenamiento de redes neuronales profundas". arXiv : 1510.06356 [quant-ph].
62. Benedetti, Marcello; Realpe-Gómez, John; Biswas, Rupak; Perdomo-Ortiz, Alejandro (2016). "Estimación de temperaturas efectivas en recocidos cuánticos para aplicaciones de muestreo: un estudio de caso con posibles aplicaciones en aprendizaje profundo". Physical Review A . 94 (2): 022308. arXiv : 1510.07611 . Código Bibliográfico :2016PhRvA..94b2308B. doi :10.1103/PhysRevA.94.022308. S2CID  118602077.
63. Korenkevych, Dmytro; Xue, Yanbo; Bian, Zhengbing; Chudak, Fabian; Macready, William G.; Rolfe, Jason; Andriyash, Evgeny (2016). "Evaluación comparativa de hardware cuántico para el entrenamiento de máquinas de Boltzmann totalmente visibles". arXiv : 1611.04528 [quant-ph].
64. Benedetti, Marcello; Realpe-Gómez, John; Biswas, Rupak; Perdomo-Ortiz, Alejandro (2017). "Aprendizaje asistido por cuántica de modelos gráficos con conectividad arbitraria por pares". Physical Review X . 7 (4): 041052. arXiv : 1609.02542 . Código Bibliográfico :2017PhRvX...7d1052B. doi :10.1103/PhysRevX.7.041052. S2CID  55331519.
65. Rocutto, Lorenzo; Destri, Claudio; Prati, Enrico (2021). "Aprendizaje semántico cuántico mediante recocido inverso de una computadora cuántica adiabática". Tecnologías cuánticas avanzadas . 4 (2): 2000133. arXiv : 2003.11945 . doi :10.1002/qute.202000133. ISSN  2511-9044. S2CID  214667224.
66. Amin, Mohammad H.; Andriyash, Evgeny; Rolfe, Jason; Kulchytskyy, Bohdan; Melko, Roger (2018). "Máquinas cuánticas Boltzmann". Física. Rev. X. 8 (21050): 021050. arXiv : 1601.02036 . Código Bib : 2018PhRvX...8b1050A. doi : 10.1103/PhysRevX.8.021050. S2CID  119198869.
67. "Phys. Rev. E 72, 026701 (2005): Recocido cuántico en un proceso cinético co…". archive.is . 2014-01-13. Archivado desde el original el 2014-01-13 . Consultado el 2018-12-07 .
68. Wiebe, Nathan; Kapoor, Ashish; Svore, Krysta M. (2014). "Aprendizaje profundo cuántico". arXiv : 1412.3489 [quant-ph].
69. Wittek, Peter; Gogolin, Christian (2017). "Inferencia cuántica mejorada en redes lógicas de Markov". Scientific Reports . 7 (45672): 45672. arXiv : 1611.08104 . Bibcode :2017NatSR...745672W. doi :10.1038/srep45672. PMC 5395824 . PMID  28422093. 
70. Gupta, Sanjay; Zia, RKP (1 de noviembre de 2001). "Redes neuronales cuánticas". Revista de ciencias de la computación y de sistemas . 63 (3): 355–383. arXiv : quant-ph/0201144 . doi :10.1006/jcss.2001.1769. ISSN  0022-0000. S2CID  206569020.
71. Ezhov, Alexandr A.; Ventura, Dan (2000), "Redes neuronales cuánticas", Future Directions for Intelligent Systems and Information Sciences , Estudios en borrosidad y computación blanda, vol. 45, Physica-Verlag HD, págs. 213-235, CiteSeerX 10.1.1.683.5972 , doi :10.1007/978-3-7908-1856-7_11, ISBN  978-3-7908-2470-4, Número de identificación del sujeto  9099722
72. Behrman, EC; Nash, LR; Steck, JE; Chandrashekar, VG; Skinner, SR (1 de octubre de 2000). "Simulaciones de redes neuronales cuánticas". Ciencias de la Información . 128 (3–4): 257–269. doi :10.1016/S0020-0255(00)00056-6. ISSN  0020-0255.
73. Henderson, Maxwell; Shakya, Samriddhi; Pradhan, Shashindra; Cook, Tristan (27 de febrero de 2020). "Redes neuronales cuaneuvolucionarias: potenciando el reconocimiento de imágenes con circuitos cuánticos". Inteligencia artificial cuántica . 2 (1). arXiv : 1904.04767 . doi :10.1007/s42484-020-00012-y. ISSN  2524-4906. S2CID  104291950.
74. Gaikwad, Akash S. Poda de redes neuronales convolucionales (SqueezeNet) para una implementación eficiente de hardware. OCLC  1197735354.
75. Cong, Iris; Choi, Soonwon; Lukin, Mikhail D. (26 de agosto de 2019). "Redes neuronales convolucionales cuánticas". Nature Physics . 15 (12): 1273–1278. arXiv : 1810.03787 . Código Bibliográfico :2019NatPh..15.1273C. doi :10.1038/s41567-019-0648-8. ISSN  1745-2473. S2CID  53642483.
76. Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. (10 de septiembre de 2018). "Aprendizaje de circuitos cuánticos". Physical Review A . 98 (3): 032309. arXiv : 1803.00745 . Código Bibliográfico :2018PhRvA..98c2309M. doi :10.1103/physreva.98.032309. hdl :11094/77645. ISSN  2469-9926. S2CID  117542570.
77. Hochreiter, Sepp; Schmidhuber, Jürgen (1 de noviembre de 1997). "Memoria a largo plazo". Computación neuronal . 9 (8): 1735–1780. doi :10.1162/neco.1997.9.8.1735. ISSN  0899-7667. PMID  9377276. S2CID  1915014.
78. Preskill, John (6 de agosto de 2018). "Computación cuántica en la era NISQ y más allá". Quantum . 2 : 79. arXiv : 1801.00862 . Bibcode :2018Quant...2...79P. doi :10.22331/q-2018-08-06-79. ISSN  2521-327X. S2CID  44098998.
79. Bacon, Dave (12 de septiembre de 2013), "Corrección de errores cuánticos experimentales", Corrección de errores cuánticos , Cambridge University Press, págs. 509-518, doi :10.1017/cbo9781139034807.023, ISBN 9780521897877, consultado el 23 de noviembre de 2022
80. Bharti, Kishor; Cervera-Lierta, Alba; Kyaw, Thi Ha; Haug, Tobías; Alperin-Lea, Sumner; Anand, Abhinav; Degroote, Matías; Heimonen, Hermanni; Kottmann, Jakob S.; Menke, Tim; Mok, Wai-Keong; Sim, Sukin; Kwek, Leong-Chuan; Aspuru-Guzik, Alán (15 de febrero de 2022). "Algoritmos cuánticos ruidosos de escala intermedia". Reseñas de Física Moderna . 94 (1): 015004. arXiv : 2101.08448 . Código Bib : 2022RvMP...94a5004B. doi : 10.1103/revmodphys.94.015004. hdl :10356/161272. ISSN  0034-6861. S2CID  231662441.
81. Grant, Edward; Benedetti, Marcello; Cao, Shuxiang; Hallam, Andrew; Lockhart, Joshua; Stojevic, Vid; Green, Andrew G.; Severini, Simone (diciembre de 2018). "Clasificadores cuánticos jerárquicos". npj Quantum Information . 4 (1): 65. arXiv : 1804.03680 . Código Bibliográfico :2018npjQI...4...65G. doi :10.1038/s41534-018-0116-9. S2CID  55479810.
82. Zhao, Chen; Gao, Xiao-Shan (4 de junio de 2021). "Análisis del fenómeno de la meseta estéril en el entrenamiento de redes neuronales cuánticas con el cálculo ZX". Quantum . 5 : 466. arXiv : 2102.01828 . Bibcode :2021Quant...5..466Z. doi :10.22331/q-2021-06-04-466. ISSN  2521-327X. S2CID  231786346.
83. Hur, Tak; Kim, Leeseok; Park, Daniel K. (10 de febrero de 2022). "Red neuronal convolucional cuántica para la clasificación clásica de datos". Inteligencia artificial cuántica . 4 (1): 3. arXiv : 2108.00661 . doi :10.1007/s42484-021-00061-x. ISSN  2524-4906. S2CID  236772493.
84. Ostaszewski, Mateusz; Grant, Edward; Benedetti, Marcello (28 de enero de 2021). "Optimización de la estructura para circuitos cuánticos parametrizados". Quantum . 5 : 391. arXiv : 1905.09692 . Bibcode :2021Quant...5..391O. doi : 10.22331/q-2021-01-28-391 . ISSN  2521-327X. S2CID  231719244.
85. Beer, Kerstin; Müller, Gabriel (11 de diciembre de 2021). "Redes antagónicas generativas cuánticas disipativas". arXiv : 2112.06088 [quant-ph].
86. J., Sharma, Kunal Cerezo, M. Cincio, Lukasz Coles, Patrick (25 de mayo de 2020). Capacidad de entrenamiento de redes neuronales cuánticas basadas en perceptrones disipativos. OCLC  1228410830.{{cite book}}: CS1 maint: multiple names: authors list (link)
87. Goodfellow, Ian J.; Pouget-Abadie, Jean; Mirza, Mehdi; Xu, Bing; Warde-Farley, David; Ozair, Sherjil; Courville, Aaron; Bengio, Yoshua (10 de junio de 2014). "Redes generativas antagónicas". arXiv : 1406.2661 [stat.ML].
88. Clark, Lewis A.; Huang W., Wei; Barlow, Thomas H.; Beige, Almut (2015). "Modelos Markov cuánticos ocultos y sistemas cuánticos abiertos con retroalimentación instantánea". En Sanayei, Ali; Rössler, Otto E.; Zelinka, Ivan (eds.). ISCS 2014: Simposio interdisciplinario sobre sistemas complejos . Emergencia, complejidad y computación. Vol. 14. págs. 131–151. arXiv : 1406.5847 . CiteSeerX 10.1.1.749.3332 . doi :10.1007/978-3-319-10759-2_16. ISBN .  978-3-319-10759-2.S2CID119226526  .​
89. Srinivasan, Siddarth; Gordon, Geoff; Boots, Byron (2018). "Aprendizaje de modelos cuánticos ocultos de Markov" (PDF) . Aistats .
90. Sentís, Gael; Guţă, Mădălin; Adesso, Gerardo (9 de julio de 2015). "Aprendizaje cuántico de estados coherentes". Tecnología cuántica EPJ . 2 (1): 17. arXiv : 1410.8700 . Código Bib : 2015EPJQT...2...17S. doi : 10.1140/epjqt/s40507-015-0030-4 .
91. Sasaki, Masahide; Carlini, Alberto (6 de agosto de 2002). "Aprendizaje cuántico y máquina de emparejamiento cuántico universal". Physical Review A . 66 (2): 022303. arXiv : quant-ph/0202173 . Código Bibliográfico :2002PhRvA..66b2303S. doi :10.1103/PhysRevA.66.022303. S2CID  119383508.
92. Bisio, Alejandro; Chiribella, Giulio; D'Ariano, Giacomo Mauro; Facchini, Stefano; Perinotti, Paolo (25 de marzo de 2010). "Aprendizaje cuántico óptimo de una transformación unitaria". Revisión física A. 81 (3): 032324. arXiv : 0903.0543 . Código Bib : 2010PhRvA..81c2324B. doi : 10.1103/PhysRevA.81.032324. S2CID  119289138.
93. Aïmeur, Esma; Brassard, Gilles; Gambs, Sébastien (1 de enero de 2007). "Algoritmos de agrupamiento cuántico". Actas de la 24.ª conferencia internacional sobre aprendizaje automático . pp. 1–8. CiteSeerX 10.1.1.80.9513 . doi :10.1145/1273496.1273497. ISBN.  978-1-59593-793-3. Número de identificación del sujeto  4357684.
94. Heese, Raoul; Gerlach, Thore; Mücke, Sascha; Müller, Sabine; Jacobs, Matías; Piatkowski, Nico (22 de enero de 2023). "Aprendizaje automático cuántico explicable". arXiv : 2301.09138 [cuántico-ph].
95. Molnar, Christoph. Aprendizaje automático interpretable.
96. Schuld, Maria; Killoran, Nathan (2 de marzo de 2022). "¿Es la ventaja cuántica el objetivo adecuado para el aprendizaje automático cuántico?". PRX Quantum . 3 (3): 030101. arXiv : 2203.01340 . Bibcode :2022PRXQ....3c0101S. doi :10.1103/PRXQuantum.3.030101. S2CID  247222732.
97. Mercaldo, F.; Ciaramella, G.; Iadarola, G.; Storto, M.; Martinelli, F.; Santone, Ao (2022). "Hacia un aprendizaje automático cuántico explicable para la detección y clasificación de malware móvil". Applied Sciences . 12 (23): 12025. doi : 10.3390/app122312025 .
98. Ribeiro, Marco Tulio; Singh, Sameer; Guestrin, Carlos (9 de agosto de 2016), "¿Por qué debería confiar en ti?": Explicando las predicciones de cualquier clasificador , arXiv : 1602.04938
99. Pira, Lirandë; Ferrie, Chris (18 de abril de 2024), Sobre la interpretabilidad de las redes neuronales cuánticas , arXiv : 2308.11098
100. Cory, DG; Wiebe, Nathan; Ferrie, Christopher; Granade, Christopher E. (6 de julio de 2012). "Aprendizaje hamiltoniano robusto en línea". New Journal of Physics . 14 (10): 103013. arXiv : 1207.1655 . Código Bibliográfico :2012NJPh...14j3013G. doi :10.1088/1367-2630/14/10/103013. S2CID  9928389.
101. Arunachalam, Srinivasan; de Wolf, Ronald (2017). "Un estudio de la teoría del aprendizaje cuántico". arXiv : 1701.06806 [quant-ph].
102. Servedio, Rocco A.; Gortler, Steven J. (2004). "Equivalencias y separaciones entre la capacidad de aprendizaje cuántico y clásico". Revista SIAM de Computación . 33 (5): 1067–1092. CiteSeerX 10.1.1.69.6555 . doi :10.1137/S0097539704412910. 
103. Arunachalam, Srinivasan; de Wolf, Ronald (2016). "Complejidad óptima de la muestra cuántica de algoritmos de aprendizaje". arXiv : 1607.00932 [quant-ph].
104. Nader, Bshouty H.; Jeffrey, Jackson C. (1999). "Aprendizaje de DNF sobre la distribución uniforme utilizando un ejemplo cuántico de Oracle". Revista SIAM de Computación . 28 (3): 1136–1153. CiteSeerX 10.1.1.23.5709 . doi :10.1137/S0097539795293123. 
105. Monrás, Alex; Sentís, Gael; Wittek, Peter (2017). "Aprendizaje cuántico supervisado inductivo". Cartas de revisión física . 118 (19): 190503. arXiv : 1605.07541 . Código bibliográfico : 2017PhRvL.118s0503M. doi :10.1103/PhysRevLett.118.190503. PMID  28548536. S2CID  6521971.
106. "Demostración NIPS 2009: Clasificación binaria mediante implementación de hardware de recocido cuántico" (PDF) . Static.googleusercontent.com . Consultado el 26 de noviembre de 2014 .
107. "Google Quantum AI Lab Team". Google Plus . 31 de enero de 2017 . Consultado el 31 de enero de 2017 .
108. "Laboratorio de Inteligencia Artificial Cuántica de la NASA". NASA . 31 de enero de 2017. Archivado desde el original el 1 de febrero de 2017 . Consultado el 31 de enero de 2017 .
109. Neigovzen, Rodion; Neves, Jorge L.; Sollacher, Rudolf; Glaser, Steffen J. (2009). "Reconocimiento de patrones cuánticos con resonancia magnética nuclear en estado líquido". Physical Review A . 79 (4): 042321. arXiv : 0802.1592 . Código Bibliográfico :2009PhRvA..79d2321N. doi :10.1103/PhysRevA.79.042321. S2CID  119115625.
110. Li, Zhaokai; Liu, Xiaomei; Xu, Nanyang; Du, Jiangfeng (2015). "Realización experimental de una máquina de vectores de soporte cuántico". Physical Review Letters . 114 (14): 140504. arXiv : 1410.1054 . Código Bibliográfico :2015PhRvL.114n0504L. doi :10.1103/PhysRevLett.114.140504. PMID  25910101. S2CID  119182770.
111. Wan, Kwok-Ho; Dahlsten, Oscar; Kristjansson, Hler; Gardner, Robert; Kim, Myungshik (2017). "Generalización cuántica de redes neuronales de propagación hacia adelante". npj Quantum Information . 3 (36): 36. arXiv : 1612.01045 . Bibcode :2017npjQI...3...36W. doi :10.1038/s41534-017-0032-4. S2CID  51685660.
112. Brunner, Daniel; Soriano, Miguel C.; Mirasso, Claudio R.; Fischer, Ingo (2013). "Procesamiento paralelo de información fotónica a velocidades de datos de gigabytes por segundo utilizando estados transitorios". Nature Communications . 4 : 1364. Bibcode :2013NatCo...4.1364B. doi :10.1038/ncomms2368. PMC 3562454 . PMID  23322052. 
113. Tezak, Nikolas; Mabuchi, Hideo (2015). "Un perceptrón coherente para el aprendizaje totalmente óptico". EPJ Quantum Technology . 2 . arXiv : 1501.01608 . Código Bibliográfico :2015arXiv150101608T. doi :10.1140/epjqt/s40507-015-0023-3. S2CID  28568346.
114. Cai, X.-D.; Wu, D.; Su, Z.-E.; Chen, M.-C.; Wang, X.-L.; Li, Li; Liu, N.-L.; Lu, C.-Y.; Pan, J.-W. (2015). "Aprendizaje automático basado en entrelazamiento en una computadora cuántica". Physical Review Letters . 114 (11): 110504. arXiv : 1409.7770 . Código Bibliográfico :2015PhRvL.114k0504C. doi :10.1103/PhysRevLett.114.110504. PMID  25839250. S2CID  44769024.
115. Pfeiffer, P.; Egusquiza, Illinois; Di Ventra, M.; Sanz, M.; Solano, E. (2016). "Memristores cuánticos". Informes científicos . 6 (2016): 29507. arXiv : 1511.02192 . Código Bib : 2016NatSR...629507P. doi :10.1038/srep29507. PMC 4933948 . PMID  27381511. 
116. Salmilehto, J.; Deppe, F.; Di Ventra, M.; Sanz, M.; Solano, E. (2017). "Memristores cuánticos con circuitos superconductores". Informes científicos . 7 (42044): 42044. arXiv : 1603.04487 . Código Bib : 2017NatSR...742044S. doi :10.1038/srep42044. PMC 5307327 . PMID  28195193. 
117. Li, Ying; Holloway, Gregory W.; Benjamin, Simon C.; Briggs, G. Andrew D.; Baugh, Jonathan; Mol, Jan A. (2017). "Un memristor cuántico simple y robusto". Physical Review B . 96 (7): 075446. arXiv : 1612.08409 . Código Bibliográfico :2017PhRvB..96g5446L. doi :10.1103/PhysRevB.96.075446. S2CID  119454549.
118. Bird, Jordan J.; Ekárt, Anikó; Faria, Diego R. (28 de octubre de 2019). "Sobre los efectos de los generadores de números pseudoaleatorios y cuánticos aleatorios en la computación blanda". Soft Computing . 24 (12). Springer Science and Business Media LLC: 9243–9256. doi : 10.1007/s00500-019-04450-0 . ISSN  1432-7643.
119. Heese, Raoul; Wolter, Moritz; Mücke, Sascha; Franken, Lukas; Piatkowski, Nico (2024). "Sobre los efectos de los números aleatorios cuánticos sesgados en la inicialización de redes neuronales artificiales". Aprendizaje automático . 113 (3): 1189–1217. arXiv : 2108.13329 . doi :10.1007/s10994-023-06490-y.
120. "Un truco cuántico con fotones aumenta la velocidad del aprendizaje automático". New Scientist . Consultado el 31 de agosto de 2021 .
121. "¿Puede el aprendizaje automático cuántico ir más allá de su propia publicidad?". Protocolo . 2020-05-04. Archivado desde el original el 2020-10-27 . Consultado el 2020-10-27 .
122. "¿Puede el aprendizaje automático cuántico ir más allá de su propia publicidad?". quantamagazine.org . 2018-01-22.