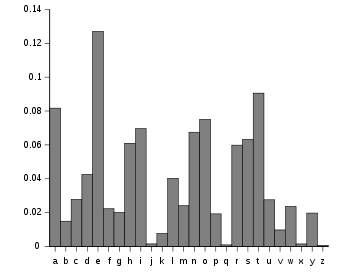
En criptoanálisis , el análisis de frecuencia (también conocido como conteo de letras ) es el estudio de la frecuencia de las letras o grupos de letras en un texto cifrado . El método se utiliza como ayuda para descifrar cifrados clásicos .
El análisis de frecuencia se basa en el hecho de que, en cualquier fragmento de lengua escrita, ciertas letras y combinaciones de letras aparecen con frecuencias variables. Además, existe una distribución característica de letras que es aproximadamente la misma para casi todas las muestras de esa lengua. Por ejemplo, dada una sección de la lengua inglesa ,mi,yo,AyOhson los más comunes, mientras queO,Q,incógnitayYoson raros. Asimismo,El,ES,EN, yUNson los pares de letras más comunes (denominados bigramas o dígrafos ), yEspartano,EE,T.T., yFFson las repeticiones más comunes. [1] La frase sin sentido " ETAOIN SHRDLU " representa las 12 letras más frecuentes en un texto típico en inglés.
En algunos cifrados, dichas propiedades del texto simple en lenguaje natural se conservan en el texto cifrado, y estos patrones tienen el potencial de ser explotados en un ataque dirigido solo al texto cifrado .
En un cifrado de sustitución simple , cada letra del texto simple se reemplaza por otra, y cualquier letra particular en el texto simple siempre se transformará en la misma letra en el texto cifrado. Por ejemplo, si todas las ocurrencias de la letramiConvertirse en la letraincógnita, un mensaje de texto cifrado que contiene numerosas instancias de la cartaincógnitaLe sugeriría a un criptoanalista queincógnitarepresentami.
El uso básico del análisis de frecuencia es contar primero la frecuencia de las letras del texto cifrado y luego asociarlas con las letras del texto simple adivinadas. Másincógnitas en el texto cifrado que cualquier otra cosa sugiere queincógnitacorresponde amien el texto claro, pero esto no es seguro;ayaTambién son muy comunes en inglés, por lo queincógnitaPodría ser cualquiera de ellos. Es poco probable que sea un texto simple.eloq, que son menos comunes. Por lo tanto, el criptoanalista puede necesitar probar varias combinaciones de asignaciones entre letras de texto cifrado y texto simple.
Se puede concebir un uso más complejo de las estadísticas, como considerar el recuento de pares de letras ( bigramas ), tripletes ( trigramas ), etc. Esto se hace para proporcionar más información al criptoanalista, por ejemplo,QytúCasi siempre aparecen juntos en ese orden en inglés, aunqueQen sí es raro.
Supongamos que Eva ha interceptado el criptograma que aparece a continuación y se sabe que está cifrado mediante un cifrado de sustitución simple:
LIVITCSWPIYVEWHEVSRIQMXLEYVEOIEWHRXEXIPFEMVEWHKVSTYLXZIXLIKIIXPIJVSZEYPERRGERIMWQLMGLMXQERIWGPSRIHMXQEREKIETXMJTPRGEVEKEITREWHEXXLEXXMZITWAWSQWXSWEXTVEPMRXRSJGSTVRIEYVIEXCVMUIMWERGMIWXMJMGCSMWXSJOMIQXLIVIQIVIXQSVSTWHKPEGARCSXRWIEVSWIIBXVIZMXFSJXLIKEGAEWHEPSWYSWIWIEVXLISXLIVXLIRGEPIRQIVIIBGIIHMWYPFLEVHEWHYPSRRFQMXLEPPXLIECCIEVEWGISJKTVWMRLIHYSPHXLIQIMYLXSJXLIMWRIGXQEROIVFVIZEVAEKPIEWHXEAMWYEPPXLMWYRMWXSGSWRMHIVEXMSWMGSTPHLEVHPFKPEZINTCMXIVJSVLMRSCMWMSWVIRCIGXMWYMX
Para este ejemplo, se utilizan letras mayúsculas para indicar texto cifrado, letras minúsculas para indicar texto simple (o suposiciones sobre el mismo) yincógnita~ase utiliza para expresar una suposición de que la letra del texto cifradoincógnitarepresenta la letra en texto planoa.
Eva podría usar el análisis de frecuencia para ayudar a resolver el mensaje de la siguiente manera: los recuentos de letras en el criptograma muestran queIes la letra única más común, [2] SGbigrama más común , yXLIes el trigrama más común .mies la letra más común en el idioma inglés,Eles el bigrama más común, yeles el trigrama más común. Esto sugiere firmemente queincógnita~a,yo~yoy I~miLa segunda letra más común en el criptograma esmi; ya que es la primera y la segunda letra más frecuente en el idioma inglés,miyase tienen en cuenta, Eva adivina quemi~a, la tercera letra más frecuente. Haciendo estas suposiciones de manera tentativa, se obtiene el siguiente mensaje parcialmente descifrado.
heVeTCSWPeYVaWHaVSReQMthaYVaOeaWHRtatePFaMVaWHKVSTYhtZetheKeetPeJVSZaYPaRRGaReM¿Qué pasa si tengo un problema con mi GPS?GSTVReaYVeatCVMUeMWaRGMeWtMJMGCSMWtSJOMeQtheVeQeVetQSVSTWHKPaGARCStRWeaVSWeeBtVeZMtFSJtheKaGAaWHaPSWYSWeaVtheStheVtheRGaPeRQeVeeBGeeHMWYPFhaVHaWHYPSRRFQMthaPPtheaCCeaVaWGeSJKTVWMRheHYSPHtheQeMYhtSJtheMWReGtQaROeVFVeZaVAaKPeaWHtaAMWYaPPthMWYRMWtSGSWRMHeVatMSWMGSTPHhaVHPFKPaZeNTCMteVJSVhMRSCMWMSWverCeGtMWYMt
Usando estas suposiciones iniciales, Eve puede detectar patrones que confirman sus elecciones, como "eso"Además, otros patrones sugieren conjeturas adicionales".Rtate"podría ser"estado", lo que significaríaR~s. Similarmente "en ese casoMZe"podría adivinarse como"En ese tiempo", cediendoMETRO~iyO~metro. Además, "élVe"podría ser"aquí", donaciónV~aAl completar estas conjeturas, Eva obtiene:
aquíTCSWPeYraWHarSseQithaYraOeaWHstatePFairaWHKrSTYhtmetheKeetPeJrSmaYPassGaseiWQhiGhitQaseWGPSseHitQasaKeaTtiJTPsGaraKaeTsaWHatthattimeTWAWSQWtSWatTraPistsSJGSTrseaYreatCriUeiWasGieWtiJiGCSiWtSJOieQthereQeretQSrSTWHKPaGAsCStsWearSWeeBtremitFSJtheKaGAaWHaPSWYSWeWeartheStherthesGaPesQereeBGeeHiWYPFharHaWHYPSssFQithaPPtheaCCearaWGeSJKTrWisheHYSPHtheQeiYhtSJtheiWseGtQasOerFremarAaKPeaWHtaAiWYaPPthiWYsiWtSGSWsiHeratiSWiGSTPHharHPFKPameNTCiterJSrhisSCiWiSWresCeGtiWYit
A su vez, estas conjeturas sugieren otras más (por ejemplo, "remarcarA"podría ser"observación", lo que implicaA~a) y así sucesivamente, y es relativamente sencillo deducir el resto de las letras, obteniendo finalmente el texto simple.
Entonces Legrand se levantó con aire solemne y majestuoso y me sacó el escarabajo de una vitrina.En el que se encontraba encerrado era un hermoso escarabajo y en ese momento era desconocido para los naturalistas.Por supuesto, un gran premio desde el punto de vista científico. Había dos puntos negros redondos cerca de un extremo.Las escamas de la espalda y de un lado a otro, cerca de la tierra, eran extremadamente duras y brillantes, con unaLa apariencia del oro bruñido y el peso del insecto eran muy notables y se llevaban todo.Teniendo en cuenta las cosas, difícilmente podría culpar a Júpiter por su opinión al respecto.
En este punto, sería una buena idea que Eve insertara espacios y puntuación:
Entonces Legrand se levantó, con aire grave y majestuoso, y me trajo el escarabajo.de una vitrina en la que estaba encerrado. Era un hermoso escarabajo y, enEn aquella época, desconocido para los naturalistas, por supuesto un gran premio desde el punto de vista científico.de vista. Había dos manchas negras redondas cerca de una extremidad de la espalda y unalargas, una cerca de la otra. Las escamas eran extremadamente duras y brillantes, con todas lasapariencia de oro bruñido. El peso del insecto era muy notable y,Teniendo en cuenta todas las cosas, difícilmente podría culpar a Júpiter por su opinión.respetandolo.
En este ejemplo de " El escarabajo del oro ", las suposiciones de Eva eran todas correctas. Sin embargo, esto no siempre sería así; la variación en las estadísticas de los textos simples individuales puede significar que las suposiciones iniciales sean incorrectas. Puede ser necesario volver atrás en las suposiciones incorrectas o analizar las estadísticas disponibles con mucha más profundidad que las justificaciones algo simplificadas que se dan en el ejemplo anterior.
Es posible que el texto simple no muestre la distribución esperada de frecuencias de letras. Es probable que los mensajes más cortos muestren más variación. También es posible construir textos sesgados artificialmente. Por ejemplo, se han escrito novelas enteras que omiten la letramien conjunto, una forma de literatura conocida como lipograma .

La primera explicación registrada conocida del análisis de frecuencia (de hecho, de cualquier tipo de criptoanálisis) fue dada en el siglo IX por Al-Kindi , un erudito árabe , en Un manuscrito sobre el descifrado de mensajes criptográficos . [3] Se ha sugerido que un estudio textual minucioso del Corán sacó a la luz por primera vez que el árabe tiene una frecuencia de letras característica. [4] Su uso se extendió y sistemas similares se usaban ampliamente en los estados europeos en la época del Renacimiento . En 1474, Cicco Simonetta había escrito un manual sobre el descifrado de cifrados de textos latinos e italianos . [5]
Los criptógrafos inventaron varios esquemas para superar esta debilidad en los cifrados de sustitución simple, entre ellos:
Una desventaja de todos estos intentos de derrotar los ataques de conteo de frecuencia es que aumentan la complejidad tanto del cifrado como del descifrado, lo que conduce a errores. Es bien sabido que un ministro de Asuntos Exteriores británico rechazó el cifrado Playfair porque, aunque los escolares pudieran manejarlo con éxito, como habían demostrado Wheatstone y Playfair, "nuestros agregados nunca podrían aprenderlo".
Las máquinas de rotor de la primera mitad del siglo XX (por ejemplo, la máquina Enigma ) eran esencialmente inmunes al análisis de frecuencias directo. Sin embargo, otros tipos de análisis ("ataques") decodificaron con éxito los mensajes de algunas de esas máquinas. [6]
El análisis de frecuencias requiere sólo una comprensión básica de las estadísticas del lenguaje de texto simple y algunas habilidades para la resolución de problemas y, si se realiza a mano, tolerancia para una contabilidad extensa de letras. Durante la Segunda Guerra Mundial , tanto los británicos como los estadounidenses reclutaron descifradores de códigos colocando crucigramas en los principales periódicos y organizando concursos para ver quién podía resolverlos más rápido. Varios de los cifrados utilizados por las potencias del Eje eran descifrables mediante análisis de frecuencia, por ejemplo, algunos de los cifrados consulares utilizados por los japoneses. Los métodos mecánicos de conteo de letras y análisis estadístico (generalmente maquinaria tipo tarjeta IBM ) se utilizaron por primera vez en la Segunda Guerra Mundial, posiblemente por el SIS del ejército de los EE. UU . Hoy, el trabajo de conteo y análisis de letras lo realiza un software de computadora , que puede realizar dicho análisis en segundos. Con la potencia informática moderna, es poco probable que los cifrados clásicos proporcionen una protección real para los datos confidenciales.

El análisis de frecuencias se ha descrito en la ficción. " El escarabajo de oro " de Edgar Allan Poe y " La aventura de los bailarines " de Sir Arthur Conan Doyle, el cuento de Sherlock Holmes, son ejemplos de historias que describen el uso del análisis de frecuencias para atacar los cifrados de sustitución simples. El cifrado en la historia de Poe está incrustado con varias medidas de engaño, pero esto es más un recurso literario que algo significativo criptográficamente.