Sistema de coordenadas transversal universal de Mercator

Sistema de proyección de mapas

La proyección universal transversal de Mercator ( UTM ) es un sistema de proyección cartográfica para asignar coordenadas a ubicaciones en la superficie de la Tierra . Al igual que el método tradicional de latitud y longitud , es una representación de posición horizontal , lo que significa que ignora la altitud y trata la superficie de la Tierra como un elipsoide perfecto . Sin embargo, se diferencia de la latitud/longitud global en que divide la Tierra en 60 zonas y proyecta cada una de ellas sobre el plano como base para sus coordenadas. Especificar una ubicación significa especificar la zona y las coordenadas x , y en ese plano. La proyección desde un esferoide a una zona UTM es una parametrización de la proyección transversal de Mercator . Los parámetros varían según la nación, la región o el sistema cartográfico.

La mayoría de las zonas en UTM abarcan 6 grados de longitud y cada una tiene un meridiano central designado. El factor de escala en el meridiano central se especifica en 0,9996 de la escala real para la mayoría de los sistemas UTM en uso. ^{[1] [2]}

Zonas UTM en un mapa mundial equirrectangular con zonas irregulares en rojo y la zona de la ciudad de Nueva York resaltada

Historia

El sitio web de la Administración Nacional Oceánica y Atmosférica (NOAA) afirma que el sistema fue desarrollado por el Cuerpo de Ingenieros del Ejército de los Estados Unidos , a principios de la década de 1940. ^[3] Sin embargo, una serie de fotos aéreas encontradas en el Bundesarchiv-Militärarchiv (la sección militar de los Archivos Federales Alemanes ) aparentemente datadas de 1943-1944 llevan la inscripción UTMREF seguida de letras y dígitos de cuadrícula, y proyectadas según el Mercator transversal, ^[4] un hallazgo que indicaría que algo llamado el sistema de referencia UTM fue desarrollado en el período de tiempo 1942-43 por la Wehrmacht . Probablemente fue llevado a cabo por el Abteilung für Luftbildwesen (Departamento de Fotografía Aérea). A partir de 1947, el Ejército de los EE. UU. empleó un sistema muy similar, pero con el factor de escala ahora estándar de 0,9996 en el meridiano central en lugar del 1,0 alemán. ^[4] Para las áreas dentro de los Estados Unidos continentales se utilizó el Elipsoide de Clarke de 1866 ^{[5] . Para las áreas restantes de la Tierra, incluyendo} Hawái , se utilizó el Elipsoide Internacional ^{[6] . El elipsoide WGS84} del Sistema Geodésico Mundial se utiliza ahora generalmente para modelar la Tierra en el sistema de coordenadas UTM, lo que significa que el norte UTM actual en un punto dado puede diferir hasta 200 metros del anterior. Para diferentes regiones geográficas, se pueden utilizar otros sistemas de referencia .

Antes del desarrollo del sistema de coordenadas universal transversal de Mercator, varias naciones europeas demostraron la utilidad de los mapas conformes basados ​​en cuadrículas al cartografiar su territorio durante el período de entreguerras . Calcular la distancia entre dos puntos en estos mapas se podía realizar más fácilmente en el campo (utilizando el teorema de Pitágoras ) de lo que era posible utilizando las fórmulas trigonométricas requeridas bajo el sistema basado en cuadrículas de latitud y longitud . En los años de posguerra, estos conceptos se extendieron al sistema de coordenadas universal transversal de Mercator/ estereográfico polar universal (UTM/UPS), que es un sistema global (o universal) de mapas basados ​​en cuadrículas.

La proyección transversal de Mercator es una variante de la proyección de Mercator , que fue desarrollada originalmente por el geógrafo y cartógrafo flamenco Gerardus Mercator en 1570. Esta proyección es conforme , lo que significa que conserva los ángulos y, por lo tanto, las formas en regiones pequeñas. Sin embargo, distorsiona la distancia y el área.

Definiciones

Zona UTM

Vista simplificada de zonas UTM contiguas de EE. UU. , proyectadas con la cónica conforme de Lambert.

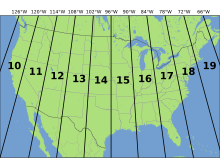
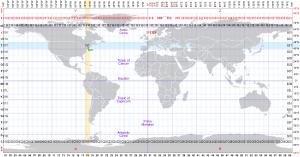
El sistema UTM divide la Tierra en 60 zonas, cada una de 6° de longitud de ancho. La zona 1 cubre la longitud de 180° a 174° O; la numeración de las zonas aumenta hacia el este hasta la zona 60, que cubre la longitud de 174° E a 180°. Las regiones polares al sur de 80° S y al norte de 84° N quedan excluidas y, en su lugar, quedan cubiertas por el sistema de coordenadas estereográficas polares universales (UPS) .

Cada una de las 60 zonas utiliza una proyección transversal de Mercator que puede representar una región de gran extensión de norte a sur con baja distorsión. Al utilizar zonas estrechas de 6° de longitud (hasta 668 km) de ancho y reducir el factor de escala a lo largo del meridiano central a 0,9996 (una reducción de 1:2500), la cantidad de distorsión se mantiene por debajo de 1 parte en 1000 dentro de cada zona. La distorsión de escala aumenta a 1,0010 en los límites de las zonas a lo largo del ecuador .

En cada zona, el factor de escala del meridiano central reduce el diámetro del cilindro transversal para producir una proyección secante con dos líneas estándar , o líneas de escala verdadera, a unos 180 km de cada lado y aproximadamente paralelas al meridiano central (Arco cos 0,9996 = 1,62° en el ecuador). La escala es menor que 1 dentro de las líneas estándar y mayor que 1 fuera de ellas, pero la distorsión general se minimiza.

Excepciones

Las zonas UTM son uniformes en todo el mundo, excepto en dos áreas. En la costa sudoeste de Noruega , la zona 32 se extiende 3° más al oeste y la zona 31 se reduce correspondientemente para cubrir solo aguas abiertas. Además, en la región alrededor de Svalbard , las zonas 32, 34 y 36 no se utilizan, mientras que las zonas 31 (9° de ancho), 33 (12° de ancho), 35 (12° de ancho) y 37 (9° de ancho) se extienden para cubrir los espacios vacíos.

Cuadrículas superpuestas

Las zonas de cuadrícula de la Universal Transverse Mercator (UTM) de 31N a 37N difieren de la zona estándar de 6° de ancho por 84° para el hemisferio norte, en parte para dar cabida a la parte occidental del Reino de Noruega. Para obtener más información sobre su historia, consulte el artículo de Clifford J. Mugnier sobre cuadrículas y datos del Reino de Noruega que apareció en la edición de octubre de 1999 de PE&RS http://www.asprs.org/a/resources/grids/10-99-norway.pdf

La distorsión de la escala aumenta en cada zona UTM a medida que se acercan los límites entre las zonas UTM. Sin embargo, a menudo es conveniente o necesario medir una serie de ubicaciones en una sola cuadrícula cuando algunas están ubicadas en dos zonas adyacentes. Alrededor de los límites de los mapas de gran escala (1:100.000 o más grandes), las coordenadas de ambas zonas UTM adyacentes suelen imprimirse dentro de una distancia mínima de 40 km a cada lado de un límite de zona. Lo ideal es que las coordenadas de cada posición se midan en la cuadrícula de la zona en la que se encuentran, pero debido a que el factor de escala sigue siendo relativamente pequeño cerca de los límites de las zonas, es posible superponer las mediciones en una zona adyacente durante cierta distancia cuando sea necesario.

Bandas de latitud

Las bandas de latitud no forman parte del UTM ^[7] , sino del sistema de referencia de cuadrícula militar (MGRS). ^[8] Sin embargo, a veces se incluyen en la notación UTM. La inclusión de bandas de latitud en la notación UTM puede dar lugar a coordenadas ambiguas (ya que la letra "S" se refiere al hemisferio sur o a una banda de latitud en el hemisferio norte) y, por lo tanto, se debe evitar.

Localizar una posición mediante coordenadas UTM

La posición en la Tierra se da mediante el número de zona UTM y el designador de hemisferio y el par de coordenadas planas este y norte en esa zona.

El punto de origen de cada zona UTM es la intersección del ecuador y el meridiano central de la zona. Para evitar trabajar con números negativos, se ha utilizado un falso Este deSe añaden −500 000 metros al meridiano central. Por lo tanto, un punto que tiene una dirección este de400 000 metros son unos 100 km al oeste del meridiano central. Para la mayoría de esos puntos, la distancia real sería ligeramente superior a 100 km, medida en la superficie de la Tierra, debido a la distorsión de la proyección. Las coordenadas UTM varían entre aproximadamente166 000 metros a834 000 metros en el ecuador.

En el hemisferio norte, las posiciones se miden hacia el norte a partir del cero en el ecuador. El valor máximo de "orientación al norte" es de aproximadamente9 300 000 metros en la latitud 84 grados Norte, el extremo norte de las zonas UTM. El norte del hemisferio sur en el ecuador se establece en10 000 000 metros. Los vientos del norte disminuyen hacia el sur desde estos10 000 000 metros a aproximadamente1 100 000 metros a 80 grados Sur, extremo sur de las zonas UTM. Por lo tanto, ningún punto tiene un valor norte negativo.

Por ejemplo, la Torre CN está en 43°38′33.24″N 79°23′13.7″O / 43.6425667, -79.387139 (Torre CN) , que está en la zona UTM 17, y la posición de la cuadrícula es630 084  m al este,4 833 438  m al norte. Dos puntos de la Zona 17 tienen estas coordenadas, uno en el hemisferio norte y otro en el sur; el formato no ambiguo es especificar el designador completo de la zona y el hemisferio, es decir, "17N 630084 4833438".

Fórmulas simplificadas

Estas fórmulas son una versión truncada de la serie de aplanamiento de Mercator transversal, que originalmente fue derivada por Johann Heinrich Louis Krüger en 1912. ^[9] Tienen una precisión de alrededor de un milímetro .3000 km del meridiano central. ^[10] También se han dado comentarios concisos para su derivación. ^{[11] [12]}

El sistema de referencia espacial WGS 84 describe la Tierra como un esferoide achatado a lo largo del eje norte-sur con un radio ecuatorial de km y un aplanamiento inverso de . Tomemos un punto de latitud y de longitud y calculemos sus coordenadas UTM, así como el factor de escala del punto y la convergencia del meridiano utilizando un meridiano de referencia de longitud . Por convención, en el hemisferio norte km y en el hemisferio sur km. Por convención también y km. ${\displaystyle a=6378.137}$ ${\displaystyle 1/f=298.257\,223\,563}$ ${\displaystyle \,\varphi }$ ${\displaystyle \,\lambda }$ ${\displaystyle k\,\!}$ ${\displaystyle \gamma \,\!}$ ${\displaystyle \lambda _{0}}$ ${\displaystyle N_{0}=0}$ ${\displaystyle N_{0}=10000}$ ${\displaystyle k_{0}=0.9996}$ ${\displaystyle E_{0}=500}$

En las siguientes fórmulas, las distancias están expresadas en kilómetros . En primer lugar, se ofrecen algunos valores preliminares:

${\displaystyle {\begin{aligned}n&={\frac {f}{2-f}},&A&={\frac {a}{1+n}}\left(1+{\frac {n^{2}}{4}}+{\frac {n^{4}}{64}}+\cdots \right),\\{}\end{aligned}}}$

${\displaystyle {\begin{aligned}\alpha _{1}&={\frac {1}{2}}n-{\frac {2}{3}}n^{2}+{\frac {5}{16}}n^{3},&\alpha _{2}&={\frac {13}{48}}n^{2}-{\frac {3}{5}}n^{3},&\alpha _{3}&={\frac {61}{240}}n^{3},\\[12pt]\beta _{1}&={\frac {1}{2}}n-{\frac {2}{3}}n^{2}+{\frac {37}{96}}n^{3},&\beta _{2}&={\frac {1}{48}}n^{2}+{\frac {1}{15}}n^{3},&\beta _{3}&={\frac {17}{480}}n^{3},\\[12pt]\delta _{1}&=2n-{\frac {2}{3}}n^{2}-2n^{3},&\delta _{2}&={\frac {7}{3}}n^{2}-{\frac {8}{5}}n^{3},&\delta _{3}&={\frac {56}{15}}n^{3}.\end{aligned}}}$

Desde latitud, longitud (φ,la) a coordenadas UTM (E, N)

Primero calculamos algunos valores intermedios:

${\displaystyle t=\sinh \left(\tanh ^{-1}\left(\sin \varphi \right)-{\frac {2{\sqrt {n}}}{1+n}}\tanh ^{-1}\left({\frac {2{\sqrt {n}}}{1+n}}\sin \varphi \right)\right),}$

${\displaystyle \xi '=\tan ^{-1}\left({\frac {t}{\cos(\lambda -\lambda _{0})}}\right),\,\,\,\eta '=\tanh ^{-1}\left({\frac {\sin(\lambda -\lambda _{0})}{\sqrt {1+t^{2}}}}\right),}$

${\displaystyle \sigma =1+\sum _{j=1}^{3}2j\alpha _{j}\cos(2j\xi ')\cosh(2j\eta '),\,\,\,\tau =\sum _{j=1}^{3}2j\alpha _{j}\sin(2j\xi ')\sinh(2j\eta ').}$

Las fórmulas finales son:

${\displaystyle E=E_{0}+k_{0}A\left(\eta '+\sum _{j=1}^{3}\alpha _{j}\cos(2j\xi ')\sinh(2j\eta ')\right),}$

${\displaystyle N=N_{0}+k_{0}A\left(\xi '+\sum _{j=1}^{3}\alpha _{j}\sin(2j\xi ')\cosh(2j\eta ')\right),}$

${\displaystyle k={\frac {k_{0}A}{a}}{\sqrt {\left\{1+\left({\frac {1-n}{1+n}}\tan \varphi \right)^{2}\right\}{\frac {\sigma ^{2}+\tau ^{2}}{t^{2}+\cos ^{2}(\lambda -\lambda _{0})}}}},}$

${\displaystyle \gamma =\tan ^{-1}\left({\frac {\tau {\sqrt {1+t^{2}}}+\sigma t\tan(\lambda -\lambda _{0})}{\sigma {\sqrt {1+t^{2}}}-\tau t\tan(\lambda -\lambda _{0})}}\right).}$

donde es Este, es Norte, es el Factor de Escala y es la Convergencia de la Red. ${\displaystyle E}$ ${\displaystyle N}$ ${\displaystyle k}$ ${\displaystyle \gamma }$

Desde coordenadas UTM (E, N, Zona, Hemi) hasta latitud, longitud (φ,la)

Nota: Hemi = +1 para el norte, Hemi = −1 para el sur

Primero calculemos algunos valores intermedios:

${\displaystyle \xi ={\frac {N-N_{0}}{k_{0}A}},\,\,\,\eta ={\frac {E-E_{0}}{k_{0}A}},}$

${\displaystyle \xi '=\xi -\sum _{j=1}^{3}\beta _{j}\sin \left(2j\xi \right)\cosh \left(2j\eta \right),\,\,\,\eta '=\eta -\sum _{j=1}^{3}\beta _{j}\cos \left(2j\xi \right)\sinh \left(2j\eta \right),}$

${\displaystyle \sigma '=1-\sum _{j=1}^{3}2j\beta _{j}\cos \left(2j\xi \right)\cosh \left(2j\eta \right),\,\,\,\tau '=\sum _{j=1}^{3}2j\beta _{j}\sin \left(2j\xi \right)\sinh \left(2j\eta \right),}$

${\displaystyle \chi =\sin ^{-1}\left({\frac {\sin \xi '}{\cosh \eta '}}\right).}$

Las fórmulas finales son:

${\displaystyle \varphi =\chi +\sum _{j=1}^{3}\delta _{j}\sin \left(2j\chi \right),}$

${\displaystyle \lambda _{0}=\mathrm {Z} \mathrm {o} \mathrm {n} \mathrm {e} \times 6^{\circ }-183^{\circ }\,}$

${\displaystyle \lambda =\lambda _{0}+\tan ^{-1}\left({\frac {\sinh \eta '}{\cos \xi '}}\right),}$

${\displaystyle k={\frac {k_{0}A}{a}}{\sqrt {\left\{1+\left({\frac {1-n}{1+n}}\tan \varphi \right)^{2}\right\}{\frac {\cos ^{2}\xi '+\sinh ^{2}\eta '}{\sigma '^{2}+\tau '^{2}}}}},}$

${\displaystyle \gamma =\mathrm {H} \mathrm {e} \mathrm {m} \mathrm {i} \times \tan ^{-1}\left({\frac {\tau '+\sigma '\tan \xi '\tanh \eta '}{\sigma '-\tau '\tan \xi '\tanh \eta '}}\right).}$

Véase también

• Sistema Europeo de Referencia Terrestre 1989 (ETRS89)
• Sistema de referencia de cuadrícula militar , una variante del UTM diseñada para simplificar la transferencia de coordenadas.
• Mercator transversal modificado , una variación del UTM utilizado en Canadá con zonas espaciadas 3° de longitud a diferencia de los 6° del UTM.
• Proyección transversal de Mercator , la proyección cartográfica utilizada por UTM.
• Sistema de coordenadas estereográficas polares universales , utilizado en los polos Norte y Sur.
• Código de Ubicación Abierta , un sistema zonificado jerárquico
• MapCode , un sistema zonificado jerárquico

Referencias

1. "Universal Transverse Mercator (UTM)". Biblioteca de software de transformación de coordenadas PROJ .^{[ enlace muerto permanente ]}
2. Snyder, John P. (1987). Proyecciones cartográficas: un manual de trabajo . Oficina de Imprenta del Gobierno de los Estados Unidos.
3. Dracup, Josef F. "Historia de la NOAA: topografía y cartografía: estudios geodésicos 1940-1990". www.history.noaa.gov . Archivado desde el original el 18 de diciembre de 2019.
4. Buchroithner, Manfred F. ; Pfahlbusch, René. Cuadrículas geodésicas en mapas fiables: nuevos hallazgos sobre el origen de la cuadrícula UTM. Cartografía y ciencia de la información geográfica, 2016, doi:10.1080/15230406.2015.1128851.
5. Radio ecuatorial 6.378.206,4 metros, radio polar 6.356.583,8 metros
6. Radio ecuatorial 6.378.388 metros, recíproco del aplanamiento 297 exactamente
7. "LAS CUADRICULAS UNIVERSALES: Universal Transverse Mercator (UTM) y Universal Polar Stereographic (UPS)" (PDF) . Agencia Nacional de Inteligencia Geoespacial . 18 de septiembre de 1989. Archivado (PDF) desde el original el 13 de febrero de 2024 . Consultado el 13 de febrero de 2024 .
8. "Lectura de mapas militares 201" (PDF) . Agencia Nacional de Inteligencia Geoespacial . 2002-05-29 . Consultado el 2009-06-19 .
9. Krüger, Luis (1912). "Konforme Abbildung des Erdellipsoids in der Ebene". Deutsches GeoForschungsZentrum GFZ. doi :10.2312/GFZ.b103-krueger28. {{cite journal}}: Requiere citar revista |journal=( ayuda )
10. Karney, Charles FF (2011). "Transversal Mercator con una precisión de unos pocos nanómetros". Journal of Geodesy . 85 (8): 475–485. arXiv : 1002.1417 . Código Bibliográfico :2011JGeod..85..475K. doi :10.1007/s00190-011-0445-3. S2CID  118619524.
11. Kawase, K. (2012): Derivación concisa de fórmulas de conversión de coordenadas extensivas en la proyección de Gauss-Krüger, Boletín de la Autoridad de Información Geoespacial de Japón , 60 , págs. 1–6
12. Kawase, K. (2011): Una fórmula general para calcular la longitud del arco meridiano y su aplicación a la conversión de coordenadas en la proyección Gauss-Krüger, Boletín de la Autoridad de Información Geoespacial de Japón, 59 , 1–13

Enlaces externos

• Coordenadas UTM en Google Maps.
• Entendiendo la proyección UTM.

Lectura adicional

• Snyder, John P. (1987). Map Projections – A Working Manual (Proyecciones cartográficas: manual de trabajo). Documento profesional 1395 del Servicio Geológico de los Estados Unidos. Imprenta del Gobierno de los Estados Unidos, Washington, D.C.