En la combinatoria poliédrica , una rama de las matemáticas, el teorema de Steinitz es una caracterización de los grafos no dirigidos formados por las aristas y vértices de poliedros convexos tridimensionales : son exactamente los grafos planos 3-conexos por vértices . Es decir, todo poliedro convexo forma un grafo plano 3-conexo, y todo grafo plano 3-conexo puede representarse como el grafo de un poliedro convexo. Por esta razón, los grafos planos 3-conexos también se conocen como grafos poliédricos . [1]
Este resultado proporciona un teorema de clasificación para los poliedros convexos tridimensionales, algo que no se conoce en dimensiones superiores. [2] Proporciona una descripción completa y puramente combinatoria de los grafos de estos poliedros, permitiendo que otros resultados sobre ellos, como el teorema de Eberhard sobre la realización de poliedros con tipos de caras dados, se puedan demostrar más fácilmente, sin referencia a la geometría de estas formas. [3] Adicionalmente, se ha aplicado en el dibujo de grafos , como una forma de construir visualizaciones tridimensionales de grafos abstractos. [4] Branko Grünbaum ha llamado a este teorema "el resultado más importante y más profundo conocido sobre 3-politopos ". [5]
El teorema aparece en una publicación de 1922 de Ernst Steinitz , [6] de quien recibe su nombre. Puede demostrarse por inducción matemática (como hizo Steinitz), hallando el estado de energía mínima de un sistema de resortes bidimensionales y elevando el resultado a tres dimensiones, o utilizando el teorema de empaquetamiento circular . Se conocen varias extensiones del teorema, en las que el poliedro que realiza un grafo dado tiene restricciones adicionales; por ejemplo, todo grafo poliédrico es el grafo de un poliedro convexo con coordenadas enteras, o el grafo de un poliedro convexo cuyos bordes son todos tangentes a una esfera media común .
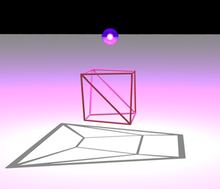
Un grafo no dirigido es un sistema de vértices y aristas , cada arista conecta dos de los vértices. Como es común en la teoría de grafos, para los propósitos del teorema de Steinitz estos grafos están restringidos a ser finitos (los vértices y las aristas son conjuntos finitos ) y simples (no hay dos aristas que conecten los mismos dos vértices, y ninguna arista conecta un vértice consigo misma). A partir de cualquier poliedro se puede formar un grafo, haciendo que los vértices del grafo correspondan a los vértices del poliedro y conectando dos vértices cualesquiera del grafo por una arista siempre que los dos vértices del poliedro correspondientes sean los puntos finales de una arista del poliedro. Este grafo se conoce como el esqueleto del poliedro. [7]
Un grafo es plano si puede dibujarse con sus vértices como puntos en el plano euclidiano y sus aristas como curvas que conectan estos puntos, de modo que ninguna de las curvas de las aristas se cruce entre sí y de modo que el punto que representa un vértice se encuentre sobre la curva que representa una arista solo cuando el vértice sea un punto final de la arista. Por el teorema de Fáry , todo dibujo plano puede enderezarse de modo que las curvas que representan las aristas sean segmentos de línea . Un grafo es 3-conexo si tiene más de tres vértices y, después de la eliminación de dos de sus vértices, cualquier otro par de vértices permanece conectado por un camino. El teorema de Steinitz establece que estas dos condiciones son necesarias y suficientes para caracterizar los esqueletos de los poliedros convexos tridimensionales: un grafo dado es el grafo de un poliedro tridimensional convexo, si y solo si es plano y conexo por 3 vértices. [5] [8]

Una dirección del teorema de Steinitz (la dirección más fácil de demostrar) establece que el gráfico de cada poliedro convexo es plano y 3-conexo. Como se muestra en la ilustración, la planaridad se puede demostrar utilizando un diagrama de Schlegel : si uno coloca una fuente de luz cerca de una cara del poliedro y un plano en el otro lado, las sombras de las aristas del poliedro formarán un gráfico plano, incrustado de tal manera que las aristas sean segmentos de línea recta. La 3-conectividad de un grafo poliédrico es un caso especial del teorema de Balinski que establece que el grafo de cualquier politopo convexo de dimensión 3 es -conexo. La conectividad del gráfico de un politopo, después de eliminar cualquiera de sus vértices, se puede demostrar eligiendo un vértice más , encontrando una función lineal que sea cero en el conjunto resultante de vértices y siguiendo los caminos generados por el método simplex para conectar cada vértice a uno de los dos vértices extremos de la función lineal, con el vértice elegido conectado a ambos. [9]
La otra dirección, más difícil, del teorema de Steinitz establece que todo grafo plano 3-conexo es el grafo de un poliedro convexo. Hay tres enfoques estándar para esta parte: pruebas por inducción, elevación de incrustaciones de Tutte bidimensionales a tres dimensiones utilizando la correspondencia de Maxwell-Cremona y métodos que utilizan el teorema de empaquetamiento de círculos para generar un poliedro canónico .

Aunque la prueba original de Steinitz no se expresó en términos de teoría de grafos, se puede reescribir en esos términos e implica encontrar una secuencia de transformaciones ΔY e YΔ que reducen cualquier grafo plano 3-conexo a , el grafo del tetraedro. Una transformación YΔ elimina un vértice de grado tres de un grafo, agregando aristas entre todos sus vecinos anteriores si esas aristas no existían ya; la transformación inversa, una transformación ΔY, elimina las aristas de un triángulo de un grafo y las reemplaza por un nuevo vértice de grado tres adyacente a los mismos tres vértices. Una vez que se encuentra dicha secuencia, se puede invertir y convertir en operaciones geométricas que construyen el poliedro deseado paso a paso a partir de un tetraedro. Cada transformación YΔ en la secuencia inversa se puede realizar geométricamente cortando un vértice de grado tres de un poliedro. Una transformación ΔY en la secuencia inversa se puede realizar geométricamente eliminando una cara triangular de un poliedro y extendiendo sus caras vecinas hasta el punto donde se encuentran, pero solo cuando ese triple punto de intersección de las tres caras vecinas está en el lado más alejado de la cara eliminada del poliedro. Cuando el triple punto de intersección no está en el lado más alejado de esta cara, una transformación proyectiva del poliedro es suficiente para moverlo al lado correcto. Por lo tanto, por inducción sobre el número de transformaciones ΔY e YΔ necesarias para reducir un grafo dado a , cada grafo poliédrico se puede realizar como un poliedro. [5]
Un trabajo posterior de Epifanov fortaleció la prueba de Steinitz de que cada grafo poliédrico puede ser reducido por transformaciones ΔY e YΔ. Epifanov demostró que si se especifican dos vértices en un grafo plano, entonces el grafo puede ser reducido a una sola arista entre esos terminales combinando transformaciones ΔY e YΔ con reducciones serie-paralelo . [10] La prueba de Epifanov era complicada y no constructiva, pero fue simplificada por Truemper usando métodos basados en menores de grafos . Truemper observó que cada grafo de cuadrícula es reducible por transformaciones ΔY e YΔ de esta manera, que esta reducibilidad se conserva por menores de grafos y que cada grafo plano es un menor de un grafo de cuadrícula. [11] Esta idea puede usarse para reemplazar el lema de Steinitz de que existe una secuencia de reducción. Después de este reemplazo, el resto de la prueba puede llevarse a cabo usando inducción de la misma manera que la prueba original de Steinitz. [8] Para estas demostraciones, llevadas a cabo utilizando cualquiera de las formas de hallar secuencias de transformaciones ΔY e YΔ, existen grafos poliédricos que requieren un número no lineal de pasos. Más precisamente, cada grafo planar puede ser reducido utilizando un número de pasos como máximo proporcional a , e infinitos grafos requieren un número de pasos como mínimo proporcional a , donde es el número de vértices en el grafo. [12] [13]
Una forma alternativa de demostración por inducción se basa en eliminar aristas (y comprimir los vértices de grado dos que pudieran quedar después de esta eliminación) o contraer aristas y formar un menor del grafo plano dado. Cualquier grafo poliédrico puede reducirse mediante un número lineal de estas operaciones, y nuevamente las operaciones pueden invertirse y las operaciones inversas pueden realizarse geométricamente, dando una realización poliédrica del grafo. Sin embargo, si bien es más simple demostrar que existe una secuencia de reducción para este tipo de argumento, y las secuencias de reducción son más cortas, los pasos geométricos necesarios para invertir la secuencia son más complicados. [14]
Si se dibuja un gráfico en el plano con aristas rectas, entonces una tensión de equilibrio se define como una asignación de números reales distintos de cero (pesos) a las aristas, con la propiedad de que cada vértice está en la posición dada por el promedio ponderado de sus vecinos. De acuerdo con la correspondencia de Maxwell-Cremona, una tensión de equilibrio se puede elevar a una superficie tridimensional continua lineal por partes de modo que las aristas que forman los límites entre las partes planas de la superficie se proyecten al dibujo dado. El peso y la longitud de cada arista determinan la diferencia en pendientes de la superficie a cada lado de la arista, y la condición de que cada vértice esté en equilibrio con sus vecinos es equivalente a la condición de que estas diferencias de pendiente hagan que la superficie se encuentre consigo misma correctamente en la vecindad del vértice. Los pesos positivos se traducen en ángulos diedros convexos entre dos caras de la superficie lineal por partes, y los pesos negativos se traducen en ángulos diedros cóncavos. A la inversa, toda superficie lineal por partes continua proviene de una tensión de equilibrio de esta manera. Si se dibuja un grafo plano finito y se le da una tensión de equilibrio de tal manera que todos los bordes interiores del dibujo tienen pesos positivos y todos los bordes exteriores tienen pesos negativos, entonces al traducir esta tensión en una superficie tridimensional de esta manera, y luego reemplazar la superficie plana que representa el exterior del grafo por su complemento en el mismo plano, se obtiene un poliedro convexo, con la propiedad adicional de que su proyección perpendicular sobre el plano no tiene cruces. [15] [16]
La correspondencia de Maxwell-Cremona se ha utilizado para obtener realizaciones poliédricas de grafos poliédricos al combinarla con un método de dibujo de grafos planos de WT Tutte , la incrustación de Tutte . El método de Tutte comienza fijando una cara de un grafo poliédrico en una posición convexa en el plano. Esta cara se convertirá en la cara exterior de un dibujo de un grafo. El método continúa estableciendo un sistema de ecuaciones lineales en las coordenadas del vértice, según el cual cada vértice restante debe colocarse en el promedio de sus vecinos. Luego, como mostró Tutte, este sistema de ecuaciones tendrá una solución única en la que cada cara del grafo se dibuja como un polígono convexo. [17] Intuitivamente, esta solución describe el patrón que se obtendría al reemplazar los bordes interiores del grafo por resortes ideales y dejar que se asienten en su estado de energía mínima. [18] El resultado es casi una tensión de equilibrio: si uno asigna un peso uno a cada borde interior, entonces cada vértice interior del dibujo está en equilibrio. Sin embargo, no siempre es posible asignar números negativos a las aristas exteriores para que también estén en equilibrio. Tal asignación siempre es posible cuando la cara exterior es un triángulo, y por lo tanto este método puede usarse para realizar cualquier grafo poliédrico que tenga una cara triangular. Si un grafo poliédrico no contiene una cara triangular, su grafo dual sí contiene un triángulo y también es poliédrico, por lo que uno puede realizar el dual de esta manera y luego realizar el grafo original como el poliedro polar de la realización dual. [4] [19] Un método alternativo para realizar poliedros usando elevaciones evita la dualidad al elegir cualquier cara con como máximo cinco vértices como la cara exterior. Cada grafo poliédrico tiene una cara así, y al elegir la forma fija de esta cara con más cuidado, se puede levantar la incrustación de Tutte del resto del grafo. [20]

Según una variante del teorema de empaquetamiento circular , para cada grafo poliédrico existe un sistema de círculos en el plano o en cualquier esfera, que representan los vértices y las caras del grafo, de modo que:
El mismo sistema de círculos forma una representación del grafo dual intercambiando los papeles de los círculos que representan vértices y los círculos que representan caras. A partir de cualquier representación de este tipo en una esfera, inserta en un espacio euclidiano tridimensional, se puede formar un poliedro convexo que es combinatoriamente equivalente al grafo dado, como una intersección de semiespacios cuyos límites pasan por los círculos de las caras. Desde cada vértice de este poliedro, el horizonte en la esfera, visto desde ese vértice, es el círculo que lo representa. Esta propiedad del horizonte determina la posición tridimensional de cada vértice, y el poliedro puede definirse de manera equivalente como la envoltura convexa de los vértices, posicionados de esta manera. La esfera se convierte en la esfera media de la realización: cada borde del poliedro es tangente a la esfera, en un punto donde dos círculos de vértice tangente cruzan dos círculos de cara tangente. [22]
Es posible probar una forma más fuerte del teorema de Steinitz, que cualquier grafo poliédrico puede ser realizado por un poliedro convexo cuyas coordenadas son números enteros . [23] Por ejemplo, la prueba original basada en la inducción de Steinitz puede ser fortalecida de esta manera. Sin embargo, los números enteros que resultarían de la construcción de Steinitz son doblemente exponenciales en el número de vértices del grafo poliédrico dado. Escribir números de esta magnitud en notación binaria requeriría un número exponencial de bits. [19] Geométricamente, esto significa que algunas características del poliedro pueden tener un tamaño doblemente exponencialmente mayor que otras, lo que hace que las realizaciones derivadas de este método sean problemáticas para aplicaciones en el dibujo de grafos . [4]
Investigadores posteriores han encontrado algoritmos de realización basados en elevación que utilizan solo un número lineal de bits por vértice. [20] [24] También es posible relajar el requisito de que las coordenadas sean números enteros y asignar coordenadas de tal manera que las coordenadas de los vértices sean números enteros distintos en el rango de 0 a y las otras dos coordenadas sean números reales en el intervalo unitario , de modo que cada arista tenga una longitud de al menos uno mientras que el poliedro general tenga un volumen lineal. [25] [26] Se sabe que algunos grafos poliédricos se pueden realizar en cuadrículas de solo tamaño polinomial; en particular, esto es cierto para las pirámides (realizaciones de grafos de rueda ), prismas (realizaciones de grafos de prisma ) y poliedros apilados (realizaciones de redes apolíneas ). [27]
Otra forma de afirmar la existencia de realizaciones enteras es que cada poliedro convexo tridimensional tiene un poliedro entero combinatoriamente equivalente. [23] Por ejemplo, el dodecaedro regular no es en sí mismo un poliedro entero, debido a sus caras de pentágono regular, pero puede realizarse como un piritoedro entero equivalente . [20] Esto no siempre es posible en dimensiones superiores, donde existen politopos (como los construidos a partir de la configuración de Perles ) que no tienen un equivalente entero. [28]
Un grafo de Halin es un caso especial de grafo poliédrico, formado a partir de un árbol incrustado en el plano (sin vértices de grado dos) conectando las hojas del árbol en un ciclo . Para los grafos de Halin, se pueden elegir realizaciones poliédricas de un tipo especial: el ciclo exterior forma una cara base convexa horizontal, y cada una de las otras caras se encuentra directamente sobre la cara base (como en los poliedros realizados mediante elevación), y todas estas caras superiores tienen la misma pendiente. Las superficies poliédricas con caras de igual pendiente sobre cualquier polígono base (no necesariamente convexo) se pueden construir a partir del esqueleto recto del polígono , y una forma equivalente de describir esta realización es que la proyección bidimensional del árbol sobre la cara base forma su esqueleto recto. La prueba de este resultado utiliza la inducción: cualquier árbol enraizado puede reducirse a un árbol más pequeño quitando las hojas de un nodo interno cuyos hijos son todos hojas, el gráfico de Halin formado a partir del árbol más pequeño tiene una realización por la hipótesis de inducción, y es posible modificar esta realización para agregar cualquier número de hijos de hojas al nodo del árbol cuyos hijos fueron eliminados. [29]
En cualquier poliedro que representa un grafo poliédrico dado , las caras de son exactamente los ciclos en que no se separan en dos componentes: es decir, eliminar un ciclo facial de deja el resto de como un subgrafo conexo. Tales ciclos se denominan ciclos periféricos . Por lo tanto, la estructura combinatoria de las caras (pero no sus formas geométricas) se determina de forma única a partir de la estructura del grafo. Otro fortalecimiento del teorema de Steinitz, por Barnette y Grünbaum, establece que para cualquier grafo poliédrico, cualquier cara del grafo y cualquier polígono convexo que represente esa cara, es posible encontrar una realización poliédrica de todo el grafo que tenga la forma especificada para la cara designada. Esto está relacionado con un teorema de Tutte, que dice que cualquier grafo poliédrico se puede dibujar en el plano con todas las caras convexas y cualquier forma especificada para su cara exterior. Sin embargo, los dibujos de grafos planos producidos por el método de Tutte no necesariamente se elevan a poliedros convexos. En cambio, Barnette y Grünbaum prueban este resultado usando un método inductivo. [30] También es siempre posible, dado un grafo poliédrico y un ciclo arbitrario en , encontrar una realización para la cual forma la silueta de la realización bajo proyección paralela . [31]
La realización de poliedros utilizando el teorema de empaquetamiento de círculos proporciona otro fortalecimiento del teorema de Steinitz: cada grafo plano 3-conexo puede representarse como un poliedro convexo de tal manera que todos sus bordes sean tangentes a la misma esfera unitaria , la esfera media del poliedro. [22] Al realizar una transformación de Möbius cuidadosamente elegida de un empaquetamiento de círculos antes de transformarlo en un poliedro, es posible encontrar una realización poliédrica que realice todas las simetrías del grafo subyacente, en el sentido de que cada automorfismo de grafo es una simetría de la realización poliédrica. [32] [33] De manera más general, si es un grafo poliédrico y es cualquier cuerpo convexo tridimensional suave , es posible encontrar una representación poliédrica de en la que todos los bordes sean tangentes a . [34]
Los métodos de empaquetamiento de círculos también se pueden utilizar para caracterizar los grafos de poliedros que tienen una circunsfera a través de todos sus vértices, o una insfera tangente a todas sus caras. (Los poliedros con una circunsfera también son significativos en geometría hiperbólica como los poliedros ideales ). En ambos casos, la existencia de una esfera es equivalente a la resolubilidad de un sistema de desigualdades lineales en variables reales positivas asociadas con cada borde del grafo. En el caso de la insfera, estas variables deben sumar exactamente uno en cada ciclo de cara del grafo, y más de uno en cada ciclo de no cara. Dualmente, para la circunsfera, las variables deben sumar uno en cada vértice, y más de uno a través de cada corte con dos o más vértices en cada lado del corte. Aunque puede haber exponencialmente muchas desigualdades lineales para satisfacer, una solución (si existe) se puede encontrar en tiempo polinomial utilizando el método del elipsoide . Los valores de las variables de una solución determinan los ángulos entre pares de círculos en un empaquetamiento circular cuyo poliedro correspondiente tiene la relación deseada con su esfera. [35] [36]

En cualquier dimensión mayor que tres, el problema algorítmico de Steinitz consiste en determinar si una red dada es la red de caras de un politopo convexo . Es poco probable que tenga complejidad de tiempo polinomial, ya que es NP-duro y más fuertemente completo para la teoría existencial de los reales , incluso para politopos de cuatro dimensiones, por el teorema de universalidad de Richter-Gebert. [38] Aquí, la teoría existencial de los reales es una clase de problemas computacionales que pueden formularse en términos de encontrar variables reales que satisfagan un sistema dado de ecuaciones e inecuaciones polinomiales. Para el problema algorítmico de Steinitz, las variables de dicho problema pueden ser las coordenadas de los vértices de un politopo, y las ecuaciones y inecuaciones pueden usarse para especificar la planitud de cada cara en la red de caras dada y la convexidad de cada ángulo entre caras. La completitud significa que cualquier otro problema de esta clase puede transformarse en una instancia equivalente del problema algorítmico de Steinitz, en tiempo polinomial. La existencia de tal transformación implica que, si el problema algorítmico de Steinitz tiene una solución en tiempo polinomial, entonces también la tiene cada problema en la teoría existencial de los reales, y cada problema en NP. [39] Sin embargo, debido a que un grafo dado puede corresponder a más de una red de caras, es difícil extender este resultado de completitud al problema de reconocer los grafos de 4-politopos. La determinación de la complejidad computacional de este problema de reconocimiento de grafos permanece abierta. [40]
Los investigadores también han encontrado caracterizaciones grafo-teóricas de los grafos de ciertas clases especiales de poliedros tridimensionales no convexos [37] [41] y politopos convexos cuatridimensionales. [40] [42] [43] Sin embargo, en ambos casos, el problema general sigue sin resolverse. De hecho, incluso el problema de determinar qué grafos completos son los grafos de poliedros no convexos (excepto para el tetraedro y para el poliedro de Császár ) sigue sin resolverse. [44]
El teorema de Eberhard caracteriza parcialmente los multiconjuntos de polígonos que pueden combinarse para formar las caras de un poliedro convexo. Puede demostrarse formando un grafo plano triconexo con el conjunto dado de caras del polígono y luego aplicando el teorema de Steinitz para encontrar una realización poliédrica de ese grafo. [3]
László Lovász ha demostrado una correspondencia entre representaciones poliédricas de grafos y matrices que realizan los invariantes de grafos de Colin de Verdière de los mismos grafos. El invariante de Colin de Verdière es el corank máximo de una matriz de adyacencia ponderada del grafo, bajo algunas condiciones adicionales que son irrelevantes para grafos poliédricos. Estas son matrices simétricas cuadradas indexadas por los vértices, con el peso del vértice en el coeficiente diagonal y con el peso de la arista en los coeficientes fuera de la diagonal y . Cuando los vértices y no son adyacentes, se requiere que el coeficiente sea cero. Este invariante es como máximo tres si y solo si el grafo es un grafo planar . Como muestra Lovász, cuando el gráfico es poliédrico, se puede obtener una representación del mismo como un poliedro encontrando una matriz de adyacencia ponderada de corank tres, encontrando tres vectores que formen una base para su espacio nulo , usando los coeficientes de estos vectores como coordenadas para los vértices de un poliedro y escalando estos vértices apropiadamente. [45]
La historia del teorema de Steinitz es descrita por Grünbaum (2007), [46] quien señala su primera aparición en forma críptica en una publicación de Ernst Steinitz , escrita originalmente en 1916. [6] Steinitz proporcionó más detalles en notas de clase posteriores, publicadas después de su muerte en 1928. Aunque los tratamientos modernos del teorema de Steinitz lo establecen como una caracterización grafo-teórica de los poliedros, Steinitz no utilizó el lenguaje de los grafos. [46] La formulación grafo-teórica del teorema fue introducida a principios de la década de 1960 por Branko Grünbaum y Theodore Motzkin , con su prueba también convertida a la teoría de grafos en el texto de Grünbaum de 1967 Convex Polytopes . [46] El trabajo de Epifanov sobre las transformaciones ΔY e YΔ , que fortalece la prueba de Steinitz, estuvo motivado por otros problemas además de la caracterización de los poliedros. Truemper (1989) atribuye a Grünbaum la observación de la relevancia de este trabajo para el teorema de Steinitz. [11]
La correspondencia de Maxwell-Cremona entre diagramas de tensión y levantamientos poliédricos fue desarrollada en una serie de artículos de James Clerk Maxwell de 1864 a 1870, basados en trabajos anteriores de Pierre Varignon , William Rankine y otros, y fue popularizada a fines del siglo XIX por Luigi Cremona . [47] La observación de que esta correspondencia se puede utilizar con la incrustación de Tutte para demostrar el teorema de Steinitz proviene de Eades y Garvan (1995); [4] véase también Richter-Gebert (1996). [38]
El teorema de empaquetamiento de círculos fue demostrado por Paul Koebe en 1936 [48] [49] y (independientemente) por EM Andreev en 1970; [49] [50] fue popularizado a mediados de la década de 1980 por William Thurston , a quien (a pesar de citar a Koebe y Andreev) a menudo se le atribuye el mérito de ser uno de sus descubridores. [49] La versión de Andreev del teorema ya estaba formulada como una caracterización similar a la de Steinitz para ciertos poliedros en el espacio hiperbólico , [50] y el uso del empaquetamiento de círculos para realizar poliedros con esferas medias proviene del trabajo de Thurston. [51] El problema de caracterizar poliedros con esferas inscritas o circunscritas, finalmente resuelto utilizando un método basado en realizaciones de empaquetamiento de círculos, se remonta al trabajo inédito de René Descartes alrededor de 1630 [52] y a Jakob Steiner en 1832; [35] [53] Los primeros ejemplos de poliedros que no tienen realización con una circunsfera o insfera fueron dados por Steinitz en 1928. [35] [54]
Abgeschlossen am 31 de agosto de 1916