Transformación YΔ y ΔY

Una operación sobre gráficos

Representación de las transformaciones ΔY e YΔ aplicadas a un gráfico

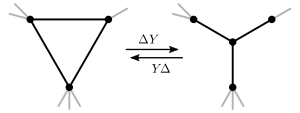
En teoría de grafos , las transformaciones ΔY e YΔ (también escritas delta-wye y wye-delta ) son un par de operaciones sobre grafos . Una transformación ΔY reemplaza un triángulo por un vértice de grado tres; y a la inversa, una transformación YΔ reemplaza un vértice de grado tres por un triángulo. Los nombres de las operaciones derivan de las formas de los subgrafos involucrados, que se parecen respectivamente a la letra Y y a la letra mayúscula griega Δ .

Una transformación YΔ puede crear aristas paralelas , incluso si se aplica a un grafo simple . Por esta razón, las transformaciones ΔY e YΔ se consideran más naturalmente como operaciones en multigrafos . En multigrafos, ambas operaciones conservan el número de aristas y son inversas exactas entre sí. En el contexto de grafos simples, es común combinar una transformación YΔ con un paso de normalización posterior que reduce las aristas paralelas a una sola arista. Esto puede no conservar el número de aristas ni ser exactamente reversible a través de una transformación ΔY.

La transformación YΔ puede generar múltiples aristas. Si se eliminan las múltiples aristas en un paso de normalización y se aplica una transformación ΔY, no se obtendrá el gráfico original.

Definición formal

Sea un gráfico (potencialmente un multigráfico). ${\displaystyle G}$

Supongamos que contiene un triángulo con vértices y aristas . Una transformación ΔY de en elimina las aristas y agrega un nuevo vértice adyacente a cada uno de . ${\displaystyle G}$ ${\displaystyle \Delta }$ ${\displaystyle x_{1},x_{2},x_{3}}$ ${\displaystyle e_{12},e_{23},e_{31}}$ ${\displaystyle G}$ ${\displaystyle \Delta }$ ${\displaystyle e_{12},e_{23},e_{31}}$ ${\displaystyle y}$ ${\displaystyle x_{1},x_{2},x_{3}}$

Por el contrario, si es un vértice de grado tres con vecinos , entonces una transformación YΔ de en elimina y agrega tres nuevos bordes , donde conecta y . Si el gráfico resultante debe ser un gráfico simple, entonces cualquier borde paralelo resultante debe reemplazarse por un solo borde. ${\displaystyle y}$ ${\displaystyle x_{1},x_{2},x_{3}}$ ${\displaystyle G}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle e_{12},e_{23},e_{31}}$ ${\displaystyle e_{ij}}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$

Pertinencia

Las transformaciones ΔY e YΔ son una herramienta tanto en la teoría de grafos pura como en sus aplicaciones.

Ambas operaciones preservan una serie de propiedades topológicas naturales de los grafos. Por ejemplo, aplicar una transformación YΔ a un vértice de 3 de un grafo plano , o una transformación ΔY a una cara triangular de un grafo plano, da como resultado nuevamente un grafo plano. ^[1] Esto se usó en la prueba original del teorema de Steinitz , que muestra que cada grafo plano 3-conexo es el grafo de arista de un poliedro . Aplicar las transformaciones ΔY e YΔ a un grafo sin enlaces da como resultado nuevamente un grafo sin enlaces. ^[2] Este hecho se usa para describir de manera compacta los menores prohibidos de las clases de grafos asociados como familias ΔY generadas a partir de un pequeño número de grafos (ver la sección sobre familias ΔY a continuación).

Existe una aplicación particularmente relevante en ingeniería eléctrica en el estudio de sistemas de potencia trifásicos (ver transformada Y-Δ (ingeniería eléctrica) ). ^[3] En este contexto también se conocen como transformaciones estrella-triángulo y son un caso especial de transformaciones estrella-malla .

Familias ΔY

Los seis miembros de la familia Petersen con aristas que denotan una aplicación de una única transformación YΔ o ΔY

La familia ΔY generada por un grafo es la familia de grafos más pequeña que contiene y está cerrada bajo las transformaciones YΔ y ΔY. De manera equivalente, se construye a partir de la aplicación recursiva de estas transformaciones hasta que no se genere ningún grafo nuevo. Si es un grafo finito, genera una familia ΔY finita, cuyos miembros tienen todos el mismo número de aristas. ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$

La familia ΔY generada por varios gráficos es la familia más pequeña que contiene todos estos gráficos y está cerrada bajo la transformación YΔ y ΔY.

Algunas familias notables se generan de esta manera:

• La familia Petersen se genera a partir del grafo completo . Está formada por los seis menores prohibidos para la clase de grafos sin enlaces. ^[2] ${\displaystyle K_{6}}$
• La familia Heawood se genera a partir de y . Consta de 78 grafos, cada uno de los cuales es un menor prohibido para la clase de grafos de 4 planos. ^[4] ${\displaystyle K_{7}}$ ${\displaystyle K_{3,3,1,1}}$

Grafos reducibles en YΔY

El gráfico formado al conectar un vértice a cada vértice de grado tres de un gráfico de dodecaedro rómbico no tiene enlaces pero no es YΔY-reducible.

Un gráfico es YΔY-reducible si puede reducirse a un solo vértice mediante una secuencia de transformaciones ΔY o YΔ y los siguientes pasos de normalización:

• Quitar un bucle ,
• eliminando un borde paralelo ,
• eliminando un vértice de grado uno,
• suavizar un vértice de grado dos, es decir, reemplazarlo por una única arista entre sus dos antiguos vecinos.

Los grafos YΔY-reducibles forman una familia cerrada de menores y por lo tanto tienen una caracterización de menores prohibidos (por el teorema de Robertson-Seymour ). Los grafos de la familia Petersen constituyen algunos (pero no todos) de los menores excluidos. ^[5] De hecho, ya se conocen más de 68 mil millones de menores excluidos. ^[6]

La clase de grafos reducibles por YΔY se encuentra entre las clases de grafos planares y grafos sin enlaces: cada grafo planares es reducible por YΔY, mientras que cada grafo reducible por YΔY es sin enlaces. Ambas inclusiones son estrictas: no es planares sino reducibles por YΔY, mientras que el grafo en la figura no es reducible por YΔY sino sin enlaces. ^[5] ${\displaystyle K_{5}}$

Referencias

1. Truemper, K. (1989). Sobre la reducción delta-wye para grafos planares. Journal of graph theory, 13(2), 141–148.
2. Robertson, Neil ; Seymour, PD ; Thomas, Robin (1993), "Incorporaciones sin enlaces de gráficos en el espacio tridimensional", Boletín de la Sociedad Matemática Americana , 28 (1): 84–89, arXiv : math/9301216 , doi :10.1090/S0273-0979-1993-00335-5, MR  1164063.
3. Johnson, DE, Hilburn, JL, Johnson, JR y Scott, PD (1986). Análisis básico de circuitos eléctricos. Englewood Cliffs: Prentice-Hall.
4. van der Holst, H. (2006). Gráficos y obstrucciones en cuatro dimensiones. Journal of Combinatorial Theory, Serie B, 96(3), 388–404.
5. Truemper, Klaus (1992), Descomposición matroide (PDF) , Academic Press, págs. 100-101
6. Yu, Y. (2006). Más menores prohibidos para la reducibilidad Wye-Delta-Wye. la revista electrónica de combinatoria, R7-R7.