Sistema autónomo (matemáticas)

Sistema de ecuaciones diferenciales ordinarias cuyo estado actual determina únicamente su evolución

Diagrama de estabilidad que clasifica los mapas de Poincaré de sistemas autónomos lineales como estables o inestables según sus características. La estabilidad generalmente aumenta hacia la izquierda del diagrama. ^{[1] Algunos} puntos de equilibrio son sumidero, fuente o nodo . ${\displaystyle x'=Ax,}$

El caso bidimensional se refiere al plano de fase .

En matemáticas , un sistema autónomo o ecuación diferencial autónoma es un sistema de ecuaciones diferenciales ordinarias que no depende explícitamente de la variable independiente . Cuando la variable es el tiempo, también se denominan sistemas invariantes en el tiempo .

Muchas leyes de la física , donde generalmente se supone que la variable independiente es el tiempo , se expresan como sistemas autónomos porque se supone que las leyes de la naturaleza que se cumplen ahora son idénticas a las de cualquier punto en el pasado o el futuro.

Definición

Un sistema autónomo es un sistema de ecuaciones diferenciales ordinarias de la forma donde x toma valores en el espacio euclidiano n -dimensional ; t se interpreta a menudo como tiempo. $${\displaystyle {\frac {d}{dt}}x(t)=f(x(t))}$$

Se distingue de los sistemas de ecuaciones diferenciales en la forma en que la ley que rige la evolución del sistema no depende únicamente del estado actual del sistema sino también del parámetro t , a menudo interpretado también como tiempo; tales sistemas, por definición, no son autónomos. $${\displaystyle {\frac {d}{dt}}x(t)=g(x(t),t)}$$

Propiedades

Las soluciones son invariantes bajo traslaciones horizontales:

Sea una solución única del problema del valor inicial para un sistema autónomo. Entonces resuelve Denotando obtiene y , por lo tanto Para la condición inicial, la verificación es trivial, ${\displaystyle x_{1}(t)}$ $${\displaystyle {\frac {d}{dt}}x(t)=f(x(t))\,,\quad x(0)=x_{0}.}$$ ${\displaystyle x_{2}(t)=x_{1}(t-t_{0})}$ $${\displaystyle {\frac {d}{dt}}x(t)=f(x(t))\,,\quad x(t_{0})=x_{0}.}$$ ${\displaystyle s=t-t_{0}}$ ${\displaystyle x_{1}(s)=x_{2}(t)}$ ${\displaystyle ds=dt}$ $${\displaystyle {\frac {d}{dt}}x_{2}(t)={\frac {d}{dt}}x_{1}(t-t_{0})={\frac {d}{ds}}x_{1}(s)=f(x_{1}(s))=f(x_{2}(t)).}$$ $${\displaystyle x_{2}(t_{0})=x_{1}(t_{0}-t_{0})=x_{1}(0)=x_{0}.}$$

Ejemplo

La ecuación es autónoma, ya que la variable independiente ( ) no aparece explícitamente en la ecuación. Para representar gráficamente el campo de pendientes y la isoclina de esta ecuación, se puede utilizar el siguiente código en GNU Octave / MATLAB ${\displaystyle y'=\left(2-y\right)y}$ ${\displaystyle x}$

Ffun = @( X , Y )( 2 - Y ) .* Y ; % function f(x,y)=(2-y)y [ X , Y ] = meshgrid ( 0 : .2 : 6 , - 1 : .2 : 3 ); % elige los tamaños de los gráficos DY = Ffun ( X , Y ); DX = ones ( size ( DY )); % genera los valores de los gráficos quiver ( X , Y , DX , DY , 'k' ); % traza el campo de dirección en negro hold on ; contour ( X , Y , DY , [ 0 1 2 ], 'g' ); % añade las isoclinas (0 1 2) en verde title ( 'Campo de pendiente e isoclinas para f(x,y)=(2-y)y' )                                 

Se puede observar en el gráfico que la función es -invariante, y también lo es la forma de la solución, es decir, para cualquier desplazamiento . ${\displaystyle \left(2-y\right)y}$ ${\displaystyle x}$ ${\displaystyle y(x)=y(x-x_{0})}$ ${\displaystyle x_{0}}$

Resolver la ecuación simbólicamente en MATLAB , ejecutando

syms y(x) ; ecuación = ( diff ( y ) == ( 2 - y ) * y ); % resuelve la ecuación para una solución general simbólicamente y_general = dsolve ( ecuación );           

obtiene dos soluciones de equilibrio , y , y una tercera solución que involucra una constante desconocida , . ${\displaystyle y=0}$ ${\displaystyle y=2}$ ${\displaystyle C_{3}}$-2 / (exp(C3 - 2 * x) - 1)

Tomando algunos valores específicos para la condición inicial , se puede agregar la gráfica de varias soluciones.

Campo de pendientes con isoclinas y soluciones

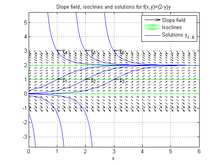
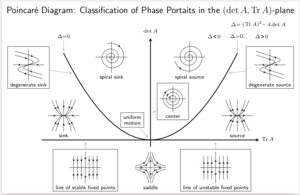
% resuelve el problema del valor inicial simbólicamente % para diferentes condiciones iniciales y1 = dsolve ( ecuación , y ( 1 ) == 1 ); y2 = dsolve ( ecuación , y ( 2 ) == 1 ); y3 = dsolve ( ecuación , y ( 3 ) == 1 ); y4 = dsolve ( ecuación , y ( 1 ) == 3 ); y5 = dsolve ( ecuación , y ( 2 ) == 3 ); y6 = dsolve ( ecuación , y ( 3 ) == 3 ); % grafica las soluciones ezplot ( y1 , [ 0 6 ]); ezplot ( y2 , [ 0 6 ]); ezplot ( y3 , [ 0 6 ]); ezplot ( y4 , [ 0 6 ]); ezplot ( y5 , [ 0 6 ]); ezplot ( y6 , [ 0 6 ]); title ( 'Campo de pendientes, isoclinas y soluciones para f(x,y)=(2-y)y' ) legend ( 'Campo de pendientes' , 'Isoclinas' , 'Soluciones y_{1..6}' ); text ([ 1 2 3 ], [ 1 1 1 ], strcat ( '\leftarrow' , { 'y_1' , 'y_2' , 'y_3' })); text ([ 1 2 3 ], [ 3 3 3 ], strcat ( '\leftarrow' , { 'y_4' , 'y_5' , 'y_6'                                                                     })); cuadrícula activada ; 

Análisis cualitativo

Los sistemas autónomos se pueden analizar cualitativamente utilizando el espacio de fases ; en el caso de una variable, esta es la línea de fase .

Técnicas de solución

Las siguientes técnicas se aplican a ecuaciones diferenciales autónomas unidimensionales. Cualquier ecuación unidimensional de orden es equivalente a un sistema de primer orden de dimensión 1 (como se describe en la reducción a un sistema de primer orden ), pero no necesariamente al revés. ${\displaystyle n}$ ${\displaystyle n}$

Primer orden

La ecuación autónoma de primer orden es separable , por lo que se puede resolver reorganizándola en la forma integral. $${\displaystyle {\frac {dx}{dt}}=f(x)}$$ $${\displaystyle t+C=\int {\frac {dx}{f(x)}}}$$

Segundo orden

La ecuación autónoma de segundo orden es más difícil, pero se puede resolver ^[2] introduciendo la nueva variable y expresando la segunda derivada de mediante la regla de la cadena como de modo que la ecuación original se convierta en que es una ecuación de primer orden que no contiene ninguna referencia a la variable independiente . La resolución proporciona como una función de . Luego, recordando la definición de : $${\displaystyle {\frac {d^{2}x}{dt^{2}}}=f(x,x')}$$ $${\displaystyle v={\frac {dx}{dt}}}$$ ${\displaystyle x}$ $${\displaystyle {\frac {d^{2}x}{dt^{2}}}={\frac {dv}{dt}}={\frac {dx}{dt}}{\frac {dv}{dx}}=v{\frac {dv}{dx}}}$$ $${\displaystyle v{\frac {dv}{dx}}=f(x,v)}$$ ${\displaystyle t}$ ${\displaystyle v}$ ${\displaystyle x}$ ${\displaystyle v}$

$${\displaystyle {\frac {dx}{dt}}=v(x)\quad \Rightarrow \quad t+C=\int {\frac {dx}{v(x)}}}$$

lo cual es una solución implícita.

Caso especial:x ″= f ( x )

El caso especial donde es independiente de ${\displaystyle f}$ ${\displaystyle x'}$

$${\displaystyle {\frac {d^{2}x}{dt^{2}}}=f(x)}$$

se beneficia de un tratamiento separado. ^[3] Este tipo de ecuaciones son muy comunes en la mecánica clásica porque siempre son sistemas hamiltonianos .

La idea es hacer uso de la identidad

$${\displaystyle {\frac {dx}{dt}}=\left({\frac {dt}{dx}}\right)^{-1}}$$

lo cual se desprende de la regla de la cadena , salvo que surjan problemas debidos a la división por cero .

Al invertir ambos lados de un sistema autónomo de primer orden, se puede integrar inmediatamente con respecto a : ${\displaystyle x}$

$${\displaystyle {\frac {dx}{dt}}=f(x)\quad \Rightarrow \quad {\frac {dt}{dx}}={\frac {1}{f(x)}}\quad \Rightarrow \quad t+C=\int {\frac {dx}{f(x)}}}$$

que es otra forma de ver la técnica de separación de variables. La segunda derivada debe expresarse como una derivada con respecto a en lugar de : ${\displaystyle x}$ ${\displaystyle t}$

$${\displaystyle {\begin{aligned}{\frac {d^{2}x}{dt^{2}}}&={\frac {d}{dt}}\left({\frac {dx}{dt}}\right)={\frac {d}{dx}}\left({\frac {dx}{dt}}\right){\frac {dx}{dt}}\\[4pt]&={\frac {d}{dx}}\left(\left({\frac {dt}{dx}}\right)^{-1}\right)\left({\frac {dt}{dx}}\right)^{-1}\\[4pt]&=-\left({\frac {dt}{dx}}\right)^{-2}{\frac {d^{2}t}{dx^{2}}}\left({\frac {dt}{dx}}\right)^{-1}=-\left({\frac {dt}{dx}}\right)^{-3}{\frac {d^{2}t}{dx^{2}}}\\[4pt]&={\frac {d}{dx}}\left({\frac {1}{2}}\left({\frac {dt}{dx}}\right)^{-2}\right)\end{aligned}}}$$

Para volver a enfatizar: lo que se ha logrado es que la segunda derivada con respecto a se ha expresado como una derivada de . La ecuación original de segundo orden ahora se puede integrar: ${\displaystyle t}$ ${\displaystyle x}$

$${\displaystyle {\begin{aligned}{\frac {d^{2}x}{dt^{2}}}&=f(x)\\{\frac {d}{dx}}\left({\frac {1}{2}}\left({\frac {dt}{dx}}\right)^{-2}\right)&=f(x)\\\left({\frac {dt}{dx}}\right)^{-2}&=2\int f(x)dx+C_{1}\\{\frac {dt}{dx}}&=\pm {\frac {1}{\sqrt {2\int f(x)dx+C_{1}}}}\\t+C_{2}&=\pm \int {\frac {dx}{\sqrt {2\int f(x)dx+C_{1}}}}\end{aligned}}}$$

Esta es una solución implícita. El mayor problema potencial es la imposibilidad de simplificar las integrales, lo que implica dificultad o imposibilidad de evaluar las constantes de integración.

Caso especial:x ″ = x′nf ( x )​^​

Utilizando el enfoque anterior, la técnica puede extenderse a la ecuación más general

$${\displaystyle {\frac {d^{2}x}{dt^{2}}}=\left({\frac {dx}{dt}}\right)^{n}f(x)}$$

donde es un parámetro distinto de dos. Esto funcionará ya que la segunda derivada se puede escribir en una forma que involucre una potencia de . Reescribiendo la segunda derivada, reordenando y expresando el lado izquierdo como una derivada: ${\displaystyle n}$ ${\displaystyle x'}$

$${\displaystyle {\begin{aligned}&-\left({\frac {dt}{dx}}\right)^{-3}{\frac {d^{2}t}{dx^{2}}}=\left({\frac {dt}{dx}}\right)^{-n}f(x)\\[4pt]&-\left({\frac {dt}{dx}}\right)^{n-3}{\frac {d^{2}t}{dx^{2}}}=f(x)\\[4pt]&{\frac {d}{dx}}\left({\frac {1}{2-n}}\left({\frac {dt}{dx}}\right)^{n-2}\right)=f(x)\\[4pt]&\left({\frac {dt}{dx}}\right)^{n-2}=(2-n)\int f(x)dx+C_{1}\\[2pt]&t+C_{2}=\int \left((2-n)\int f(x)dx+C_{1}\right)^{\frac {1}{n-2}}dx\end{aligned}}}$$

El derecho llevará +/− si es par. El tratamiento debe ser diferente si : ${\displaystyle n}$ ${\displaystyle n=2}$

$${\displaystyle {\begin{aligned}-\left({\frac {dt}{dx}}\right)^{-1}{\frac {d^{2}t}{dx^{2}}}&=f(x)\\-{\frac {d}{dx}}\left(\ln \left({\frac {dt}{dx}}\right)\right)&=f(x)\\{\frac {dt}{dx}}&=C_{1}e^{-\int f(x)dx}\\t+C_{2}&=C_{1}\int e^{-\int f(x)dx}dx\end{aligned}}}$$

Órdenes superiores

No existe un método análogo para resolver ecuaciones autónomas de tercer orden o de orden superior. Dichas ecuaciones solo se pueden resolver con exactitud si tienen alguna otra propiedad simplificadora, por ejemplo, linealidad o dependencia del lado derecho de la ecuación solo de la variable dependiente ^{[4] [5]} (es decir, no de sus derivadas). Esto no debería sorprender, considerando que los sistemas autónomos no lineales en tres dimensiones pueden producir un comportamiento verdaderamente caótico , como el atractor de Lorenz y el atractor de Rössler .

De la misma manera, las ecuaciones generales no autónomas de segundo orden no se pueden resolver explícitamente, ya que también pueden ser caóticas, como en un péndulo forzado periódicamente. ^[6]

Caso multivariado

En , donde es un vector columna -dimensional que depende de . ${\displaystyle \mathbf {x} '(t)=A\mathbf {x} (t)}$ ${\displaystyle \mathbf {x} (t)}$ ${\displaystyle n}$ ${\displaystyle t}$

La solución es donde es un vector constante. ^[7] ${\displaystyle \mathbf {x} (t)=e^{At}\mathbf {c} }$ ${\displaystyle \mathbf {c} }$ ${\displaystyle n\times 1}$

Duraciones finitas

Para las EDO autónomas no lineales es posible, bajo ciertas condiciones, desarrollar soluciones de duración finita, ^[8] lo que significa que, a partir de su propia dinámica, el sistema alcanzará el valor cero en un tiempo final y permanecerá allí en cero para siempre. Estas soluciones de duración finita no pueden ser funciones analíticas en toda la línea real y, debido a que serán funciones no Lipschitz en el tiempo final, no resisten ^{[ aclaración necesaria ]} la unicidad de las soluciones de las ecuaciones diferenciales de Lipschitz.

Como ejemplo, la ecuación:

${\displaystyle y'=-{\text{sgn}}(y){\sqrt {|y|}},\,\,y(0)=1}$

Admite la solución de duración finita:

${\displaystyle y(x)={\frac {1}{4}}\left(1-{\frac {x}{2}}+\left|1-{\frac {x}{2}}\right|\right)^{2}}$

Véase también

• Sistema no autónomo (matemáticas)

Referencias

1. Matemáticas Egwald - Álgebra lineal: sistemas de ecuaciones diferenciales lineales: análisis de estabilidad lineal Consultado el 10 de octubre de 2019.
2. Boyce, William E.; Richard C. DiPrima (2005). Ecuaciones diferenciales elementales y problemas de volumen límite (8.ª ed.). John Wiley & Sons. pág. 133. ISBN 0-471-43338-1.
3. "Ecuación autónoma de segundo orden" (PDF) . Eqworld . Consultado el 28 de febrero de 2021 .
4. Ecuación autónoma de tercer orden en eqworld .
5. Ecuación autónoma de cuarto orden en eqworld .
6. Blanchard; Devaney ; Hall (2005). Ecuaciones diferenciales . Brooks/Cole Publishing Co., págs. 540-543. ISBN 0-495-01265-3.
7. "Método de la matriz exponencial". Math24 . Consultado el 28 de febrero de 2021 .
8. Vardia T. Haimo (1985). "Ecuaciones diferenciales de tiempo finito". 1985 24th IEEE Conference on Decision and Control . págs. 1729–1733. doi :10.1109/CDC.1985.268832. S2CID  45426376.