Poder de frenado (radiación de partículas)

Fuerza retardante que actúa sobre partículas cargadas debido a interacciones con la materia.

En física nuclear y de materiales , el poder de frenado es la fuerza retardante que actúa sobre partículas cargadas , típicamente partículas alfa y beta , debido a la interacción con la materia , lo que resulta en la pérdida de energía cinética de la partícula . ^{[1] [2]} El poder de frenado también se interpreta como la velocidad a la que un material absorbe la energía cinética de una partícula cargada . Su aplicación es importante en una amplia gama de áreas termodinámicas, como la protección radiológica , la implantación de iones y la medicina nuclear . ^[3]

Gráfico que muestra las relaciones entre la radiactividad y la radiación ionizante detectada

Definición y curva de Bragg

Tanto las partículas cargadas como las no cargadas pierden energía al atravesar la materia. Los iones positivos se consideran en la mayoría de los casos a continuación. El poder de frenado depende del tipo y la energía de la radiación y de las propiedades del material por el que pasa. Dado que la producción de un par de iones (normalmente un ion positivo y un electrón (negativo)) requiere una cantidad fija de energía (por ejemplo, 33,97 eV en aire seco ^{[4] : 305} ), el número de ionizaciones por longitud de trayectoria es proporcional al poder de frenado. El poder de frenado del material es numéricamente igual a la pérdida de energía E por unidad de longitud de trayectoria, x :

${\displaystyle S(E)=-dE/dx}$

El signo menos hace que S sea positivo.

Curva de Bragg de partículas alfa de 5,49 MeV en el aire

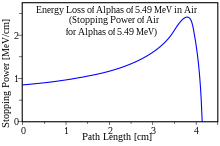
La fuerza suele aumentar hacia el final del rango y alcanza un máximo, el pico de Bragg , poco antes de que la energía caiga a cero. La curva que describe la fuerza en función de la profundidad del material se denomina curva de Bragg . Esto tiene una gran importancia práctica para la radioterapia .

La ecuación anterior define el poder de frenado lineal que en el sistema internacional se expresa en N pero que normalmente se indica en otras unidades como M eV /mm o similares. Si se compara una sustancia en forma gaseosa y sólida, entonces los poderes de frenado lineal de los dos estados son muy diferentes simplemente por la diferente densidad. Por lo tanto, a menudo se divide la fuerza por la densidad del material para obtener el poder de frenado másico que en el sistema internacional se expresa en m ⁴ / s ² pero que normalmente se encuentra en unidades como MeV/(mg/cm ² ) o similares. El poder de frenado másico depende entonces muy poco de la densidad del material.

La imagen muestra cómo el poder de frenado de las partículas alfa de 5,49 MeV aumenta a medida que la partícula atraviesa el aire, hasta alcanzar el máximo. Esta energía particular corresponde a la radiación de las partículas alfa del gas radiactivo natural radón ( ²²² Rn), que está presente en el aire en cantidades mínimas.

El rango medio se puede calcular integrando la potencia de frenado recíproca sobre la energía: ^[5]

${\displaystyle \Delta x=\int _{0}^{E_{0}}{\frac {1}{S(E)}}\,dE}$

dónde:

E ₀ es la energía cinética inicialde la partícula

Δ x es el rango de "aproximación de desaceleración continua (CSDA)" y

S ( E ) es la potencia de frenado lineal.

La energía depositada se puede obtener integrando el poder de frenado a lo largo de toda la longitud del recorrido del ion mientras se mueve en el material.

Detención electrónica, nuclear y radiactiva

El frenado electrónico se refiere a la desaceleración de un ion proyectil debido a las colisiones inelásticas entre los electrones ligados en el medio y el ion que se mueve a través de él. El término inelástico se utiliza para indicar que se pierde energía durante el proceso (las colisiones pueden dar lugar tanto a excitaciones de los electrones ligados del medio como a excitaciones de la nube de electrones del ion). La potencia de frenado electrónico lineal es idéntica a la transferencia de energía lineal sin restricciones .

En lugar de transferencia de energía, algunos modelos consideran la potencia de frenado electrónica como transferencia de momento entre el gas de electrones y el ion energético. Esto es coherente con el resultado de Bethe en el rango de alta energía. ^[6]

Dado que el número de colisiones que experimenta un ion con electrones es grande, y dado que el estado de carga del ion mientras atraviesa el medio puede cambiar con frecuencia, es muy difícil describir todas las interacciones posibles para todos los estados de carga de iones posibles. En cambio, la potencia de frenado electrónico a menudo se da como una función simple de la energía que es un promedio tomado de todos los procesos de pérdida de energía para diferentes estados de carga. Se puede determinar teóricamente con una precisión de unos pocos % en el rango de energía por encima de varios cientos de keV por nucleón a partir de tratamientos teóricos, siendo el más conocido la fórmula de Bethe . A energías inferiores a aproximadamente 100 keV por nucleón, se vuelve más difícil determinar el frenado electrónico utilizando modelos analíticos. ^{[7] Recientemente} , la teoría funcional de la densidad dependiente del tiempo en tiempo real se ha utilizado con éxito para determinar con precisión el frenado electrónico para varios sistemas ion-objetivo en un amplio rango de energías, incluido el régimen de baja energía. ^{[8] [9]} ${\displaystyle F_{e}(E)}$

Poder de frenado electrónico y nuclear para iones de aluminio en aluminio, en función de la energía de las partículas por nucleón. El máximo de la curva de frenado nuclear se produce normalmente a energías del orden de 1 keV por nucleón .

Paul ha realizado representaciones gráficas de valores experimentales del poder de frenado electrónico para muchos iones en muchas sustancias. ^[10] La precisión de varias tablas de frenado se ha determinado mediante comparaciones estadísticas. ^[11]

El poder de frenado nuclear se refiere a las colisiones elásticas entre el ion del proyectil y los átomos en la muestra (la designación establecida "nuclear" puede ser confusa ya que el frenado nuclear no se debe a fuerzas nucleares, ^[12] pero tiene la intención de señalar que este tipo de frenado implica la interacción del ion con los núcleos en el objetivo). Si uno conoce la forma de la energía potencial repulsiva entre dos átomos (ver a continuación), es posible calcular el poder de frenado nuclear . En la figura de poder de frenado que se muestra arriba para iones de aluminio en aluminio, el frenado nuclear es insignificante excepto en la energía más baja. El frenado nuclear aumenta cuando aumenta la masa del ion. En la figura que se muestra a la derecha, el frenado nuclear es mayor que el frenado electrónico a baja energía. Para iones muy ligeros que se desaceleran en materiales pesados, el frenado nuclear es más débil que el electrónico en todas las energías. ${\displaystyle E(r)}$ ${\displaystyle F_{n}(E)}$

Especialmente en el campo de daños por radiación en detectores, el término " pérdida de energía no ionizante " (NIEL) se utiliza como un término opuesto a la transferencia de energía lineal (LET), véanse, por ejemplo, las referencias. ^{[13] [14] [15]} Dado que, por definición, la potencia de frenado nuclear no implica excitaciones electrónicas, la NIEL y el frenado nuclear pueden considerarse la misma cantidad en ausencia de reacciones nucleares.

Por lo tanto, la potencia de frenado total no relativista es la suma de dos términos: . Se han ideado varias fórmulas de potencia de frenado semiempíricas. El modelo propuesto por Ziegler, Biersack y Littmark (el llamado frenado "ZBL", véase el capítulo siguiente), ^{[16] [17]} implementado en diferentes versiones de los códigos TRIM/SRIM , ^[18] es el que se utiliza con más frecuencia en la actualidad. ${\displaystyle F(E)=F_{e}(E)+F_{n}(E)}$

El poder de frenado radiativo , que se debe a la emisión de radiación de frenado en los campos eléctricos de las partículas en el material atravesado, debe considerarse a energías iónicas extremadamente altas. ^[12] Para los proyectiles de electrones, el frenado radiativo siempre es importante. A energías iónicas altas, también puede haber pérdidas de energía debido a reacciones nucleares, pero tales procesos normalmente no se describen mediante el poder de frenado. ^[12]

Cerca de la superficie de un material objetivo sólido, tanto la detención nuclear como la electrónica pueden provocar pulverización catódica .

El proceso de desaceleración en sólidos

Ilustración de la desaceleración de un solo ion en un material sólido

Al principio del proceso de desaceleración a altas energías, el ion se desacelera principalmente por detención electrónica y se mueve casi en línea recta. Cuando el ion se ha desacelerado lo suficiente, las colisiones con núcleos (detención nuclear) se vuelven cada vez más probables, dominando finalmente la desaceleración. Cuando los átomos del sólido reciben energías de retroceso significativas cuando son golpeados por el ion, se retiran de sus posiciones reticulares y producen una cascada de colisiones adicionales en el material. Estas cascadas de colisiones son la principal causa de producción de daños durante la implantación de iones en metales y semiconductores.

Cuando las energías de todos los átomos del sistema han caído por debajo del umbral de energía de desplazamiento , cesa la producción de nuevos daños y el concepto de detención nuclear ya no tiene sentido. La cantidad total de energía depositada por las colisiones nucleares sobre los átomos de los materiales se denomina energía nuclear depositada.

El recuadro de la figura muestra una distribución típica de los iones depositados en el sólido. El caso que se muestra aquí podría ser, por ejemplo, la desaceleración de un ion de silicio de 1 MeV en silicio. El rango medio para un ion de 1 MeV está típicamente en el rango micrométrico .

Repulsivopotenciales interatómicos

A distancias muy pequeñas entre los núcleos, la interacción repulsiva puede considerarse esencialmente coulombiana. A distancias mayores, las nubes de electrones apantallan los núcleos entre sí. Por lo tanto, el potencial repulsivo puede describirse multiplicando la repulsión coulombiana entre núcleos por una función de apantallamiento φ(r/a),

${\displaystyle V(r)={1 \over 4\pi \varepsilon _{0}}{Z_{1}Z_{2}e^{2} \over r}\varphi (r/a)}$

donde φ(r/a) → 1 cuando r → 0. Aquí y son las cargas de los núcleos que interactúan, y r la distancia entre ellos; a es el llamado parámetro de apantallamiento. ${\displaystyle Z_{1}}$ ${\displaystyle Z_{2}}$

A lo largo de los años se han propuesto una gran cantidad de potenciales repulsivos y funciones de apantallamiento diferentes, algunos determinados de forma semiempírica y otros a partir de cálculos teóricos. Un potencial repulsivo muy utilizado es el propuesto por Ziegler, Biersack y Littmark, el denominado potencial repulsivo ZBL. Se ha construido ajustando una función de apantallamiento universal a potenciales obtenidos teóricamente calculados para una gran variedad de pares de átomos. ^[16] El parámetro y la función de apantallamiento ZBL tienen las formas

${\displaystyle a=a_{u}={0.8854a_{0} \over Z_{1}^{0.23}+Z_{2}^{0.23}}}$

y

${\displaystyle \varphi (x)=0.1818e^{-3.2x}+0.5099e^{-0.9423x}+0.2802e^{-0.4029x}+0.02817e^{-0.2016x}}$

donde x = r/a _u , y a ₀ es el radio atómico de Bohr = 0,529 Å.

La desviación estándar del ajuste del potencial repulsivo universal ZBL a los potenciales específicos de pares calculados teóricamente a los que se ajusta es del 18 % por encima de 2 eV. ^[16] Se pueden obtener potenciales repulsivos aún más precisos a partir de cálculos de energía total autoconsistentes utilizando la teoría funcional de la densidad y la aproximación de densidad local (LDA) para el intercambio y correlación electrónicos. ^[19]

Canalización

En los materiales cristalinos, en algunos casos, el ion puede "canalizarse", es decir, enfocarse en un canal entre los planos cristalinos donde casi no experimenta colisiones con los núcleos. ^[20] Además, el poder de frenado electrónico puede ser más débil en el canal. ^[21] Por lo tanto, el frenado nuclear y electrónico no solo dependen del tipo y la densidad del material, sino también de su estructura microscópica y sección transversal.

Simulaciones por computadora de desaceleración de iones

Los métodos de simulación por ordenador para calcular el movimiento de iones en un medio se han desarrollado desde la década de 1960 y ahora son la forma dominante de tratar teóricamente el poder de frenado. La idea básica de estos métodos es seguir el movimiento del ion en el medio simulando las colisiones con los núcleos del medio. El poder de frenado electrónico suele tenerse en cuenta como una fuerza de fricción que frena el ion.

Los métodos convencionales utilizados para calcular los rangos de iones se basan en la aproximación de colisión binaria (BCA). ^[22] En estos métodos, el movimiento de iones en la muestra implantada se trata como una sucesión de colisiones individuales entre el ion de retroceso y los átomos en la muestra. Para cada colisión individual, la integral de dispersión clásica se resuelve mediante integración numérica.

El parámetro de impacto p en la integral de dispersión se determina a partir de una distribución estocástica o de una manera que tenga en cuenta la estructura cristalina de la muestra. El primer método es adecuado únicamente en simulaciones de implantación en materiales amorfos, ya que no tiene en cuenta la canalización.

El programa de simulación BCA más conocido es TRIM/SRIM ( acrónimo de TRansport of Ions in Matter, en versiones más recientes llamado Stopping and Range of Ions in Matter), que se basa en el frenado electrónico ZBL y el potencial interatómico . ^{[16] [18] [23]} Tiene una interfaz de usuario muy fácil de usar, y tiene parámetros predeterminados para todos los iones en todos los materiales hasta una energía iónica de 1 GeV, lo que lo ha hecho inmensamente popular. Sin embargo, no tiene en cuenta la estructura cristalina, lo que limita severamente su utilidad en muchos casos. Varios programas BCA superan esta dificultad; algunos bastante conocidos son MARLOWE, ^[24] BCCRYS y crystal-TRIM.

Aunque los métodos BCA se han utilizado con éxito para describir muchos procesos físicos, presentan algunos obstáculos para describir el proceso de desaceleración de iones energéticos de forma realista. La suposición básica de que las colisiones son binarias da lugar a graves problemas cuando se intenta tener en cuenta múltiples interacciones. Además, al simular materiales cristalinos, el proceso de selección del siguiente átomo reticular que colisiona y el parámetro de impacto p siempre implican varios parámetros que pueden no tener valores perfectamente bien definidos, lo que puede afectar los resultados en un 10-20% incluso para elecciones aparentemente bastante razonables de los valores de los parámetros. La mejor fiabilidad en BCA se obtiene incluyendo múltiples colisiones en los cálculos, lo que no es fácil de hacer correctamente. Sin embargo, al menos MARLOWE lo hace.

Una forma fundamentalmente más sencilla de modelar colisiones atómicas múltiples es la que proporcionan las simulaciones de dinámica molecular (MD), en las que se calcula la evolución temporal de un sistema de átomos resolviendo numéricamente las ecuaciones de movimiento. Se han ideado métodos MD especiales en los que se ha reducido el número de interacciones y átomos implicados en las simulaciones MD para que sean lo suficientemente eficientes para calcular rangos de iones. ^{[25] [26]} Las simulaciones MD describen automáticamente el poder de frenado nuclear. El poder de frenado electrónico se puede incluir fácilmente en las simulaciones de dinámica molecular, ya sea como una fuerza de fricción ^{[25] [27] [ 28] [29] [26] [30] [31] [32]} o de una manera más avanzada siguiendo también el calentamiento de los sistemas electrónicos y acoplando los grados de libertad electrónicos y atómicos. ^{[33] [34] [35]}

Partícula ionizante mínima

Más allá del máximo, el poder de frenado disminuye aproximadamente como 1/v ² con el aumento de la velocidad de la partícula v , pero después de un mínimo, aumenta de nuevo. ^[36] Una partícula ionizante mínima (MIP) es una partícula cuya tasa media de pérdida de energía a través de la materia está cerca del mínimo. En muchos casos prácticos, las partículas relativistas (por ejemplo, los muones de rayos cósmicos ) son partículas ionizantes mínimas. Una propiedad importante de todas las partículas ionizantes mínimas es que es aproximadamente verdadera donde y son las cantidades cinemáticas relativistas habituales. Además, todas las MIP tienen casi la misma pérdida de energía en el material cuyo valor es: . ^[36] ${\displaystyle \beta \gamma \simeq 3}$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ ${\displaystyle -{\frac {dE}{dx}}\simeq 2{\frac {\text{MeV}}{\mathrm {g} \,{\text{cm}}^{-2}}}}$

Véase también

• Longitud de radiación
• Longitud de atenuación
• Cascada de colisiones
• Ciencia de los materiales de radiación

Referencias

1. Bragg, WH (1905). "Sobre las partículas α del radio y su pérdida de alcance al pasar a través de varios átomos y moléculas". Phil. Mag . 10 (57): 318. doi :10.1080/14786440509463378.
2. Bohr, N. (1913). "Sobre la teoría de la disminución de la velocidad de las partículas electrificadas en movimiento al atravesar la materia". Phil. Mag . 25 (145): 10. doi :10.1080/14786440108634305.
3. Informe ICRU 73: Detención de iones más pesados ​​que el helio, Journal of the ICRU, 5 No. 1 (2005), Oxford Univ. Press ISBN 0-19-857012-0 
4. Podgorsak, EB, ed. (2005). Física de la oncología radioterápica: Manual para profesores y estudiantes (PDF) . Viena: Organismo Internacional de Energía Atómica. ISBN 978-92-0-107304-4. Recuperado el 25 de noviembre de 2012 .
5. Comisión Internacional de Unidades y Medidas de Radiación (1970). Transferencia de energía lineal (PDF) . Washington DC ISBN 978-0913394090. Informe ICRU 16 . Consultado el 1 de diciembre de 2012 .{{cite book}}: CS1 maint: location missing publisher (link)
6. Yang, C.; Di Li, Di Li; Geng Wang, Geng Wang; Li Lin, Li Lin; Tasch, AF; Banerjee, S. (2002). "Modelo mecánico cuántico del poder de frenado electrónico para iones en un gas de electrones libres". Tecnología de implantación de iones. 2002. Actas de la 14.ª Conferencia internacional sobre . págs. 556–559. doi :10.1109/IIT.2002.1258065. ISBN 0-7803-7155-0. Número de identificación del sujeto  117936302.
7. P. Sigmund: Detención de iones pesados. Springer Tracts in Modern Physics Vol. 204 (2004) ISBN 3-540-22273-1 
8. Zeb, M. Ahsan; Kohanoff, J.; Sánchez-Portal, D.; Arnau, A.; Juaristi, JI; Artacho, Emilio (31 de mayo de 2012). "Poder de frenado electrónico en oro: el papel de los electrones d y la anomalía H/He". Physical Review Letters . 108 (22): 225504. arXiv : 1205.1728 . Código Bibliográfico :2012PhRvL.108v5504Z. doi :10.1103/PhysRevLett.108.225504. PMID  23003620. S2CID  2682651.
9. Ullah, Rafi; Corsetti, Fabiano; Sánchez-Portal, Daniel; Artacho, Emilio (2015-03-11). "Poder de frenado electrónico en un semiconductor de banda estrecha a partir de primeros principios". Physical Review B . 91 (12): 125203. arXiv : 1410.6642 . Código Bibliográfico :2015PhRvB..91l5203U. doi :10.1103/PhysRevB.91.125203. S2CID  31233417.
10. "Poder de frenado de los iones ligeros". Archivado desde el original el 6 de febrero de 2012. Consultado el 19 de febrero de 2014 .
11. Paul, H (2006). "Una comparación de tablas de poder de frenado recientes para iones ligeros y medio-pesados ​​con datos experimentales y aplicaciones a la dosimetría de radioterapia". Nuclear Instruments and Methods in Physics Research B . 247 (2): 166–172. Bibcode :2006NIMPB.247..166P. doi :10.1016/j.nimb.2006.01.059.
12. Comisión Internacional de Unidades y Medidas de Radiación (octubre de 2011). Seltzer, Stephen M. (ed.). "Fundamental Quantities and Units for Ionizing Radiation" (PDF) . Journal of the ICRU . 11 (1) (edición revisada): NP.2–NP. doi :10.1093/jicru/ndr012. PMID  24174259. Informe 85a de la ICRU . Consultado el 14 de diciembre de 2012 .^{[ enlace muerto permanente ]}
13. Huhtinen, Mika (2002). "Simulación de la pérdida de energía no ionizante y la formación de defectos en silicio". Nuclear Instruments and Methods in Physics Research B . 491 (1–2): 194–215. Bibcode :2002NIMPA.491..194H. doi :10.1016/s0168-9002(02)01227-5.
14. Barry, AL; Houdayer, AJ; Hinrichsen, PF; Letourneau, WG; Vincent, J (1995). "La dependencia energética de las constantes de daño de por vida en LED de GaAs para protones de 1-500 MeV". IEEE Transactions on Nuclear Science . 42 (6): 2104–2107. Bibcode :1995ITNS...42.2104B. doi :10.1109/23.489259.
15. Lindström, G (2001). "Detectores de silicio duro de radiación: desarrollos de la colaboración RD48 (ROSE)". Nuclear Instruments and Methods in Physics Research A . 466 (2): 308–326. Bibcode :2001NIMPA.466..308L. doi :10.1016/S0168-9002(01)00560-5. hdl : 11568/67464 .
16. JF Ziegler, JP Biersack y U. Littmark. En The Stopping and Range of Ions in Matter, volumen 1, Nueva York, 1985. Pergamon. ISBN 0-08-022053-3 
17. JF Ziegler, JP Biersack y MD Ziegler: SRIM - La detención y el rango de iones en la materia, SRIM Co., 2008. ISBN 0-9654207-1-X 
18. Sitio web de SRIM
19. Nordlund, K; Runeberg, N; Sundholm, D (1997). "Potenciales interatómicos repulsivos calculados utilizando métodos de teoría de Hartree-Fock y funcional de la densidad". Nuclear Instruments and Methods in Physics Research B . 132 (1): 45. Bibcode :1997NIMPB.132...45N. doi :10.1016/S0168-583X(97)00447-3.
20. Eisen, FH (15 de marzo de 1968). "Canalización de iones de masa media a través del silicio". Revista canadiense de física . 46 (6): 561–572. doi :10.1139/p68-070. ISSN  0008-4204.
21. Ntemou, Eleni; Holeňák, Radek; Primetzhofer, Daniel (1 de mayo de 2022). "Deposición de energía por iones H y He a energías de keV en láminas de SiC monocristalinas autoportantes". Física y química de la radiación . 194 : 110033. doi :10.1016/j.radphyschem.2022.110033. ISSN  0969-806X.
22. Robinson, Mark; Torrens, Ian (1974). "Simulación por computadora de cascadas de desplazamiento atómico en sólidos en la aproximación de colisión binaria". Physical Review B . 9 (12): 5008. Bibcode :1974PhRvB...9.5008R. doi :10.1103/PhysRevB.9.5008.
23. Biersack, J; Haggmark, L (1980). "Un programa informático de Monte Carlo para el transporte de iones energéticos en objetivos amorfos☆". Nuclear Instruments and Methods . 174 (1): 257. Bibcode :1980NucIM.174..257B. doi :10.1016/0029-554X(80)90440-1.
24. Robinson, M (1992). "Estudios de simulación por ordenador de cascadas de colisiones de alta energía1". Nuclear Instruments and Methods in Physics Research B . 67 (1–4): 396–400. Bibcode :1992NIMPB..67..396R. doi :10.1016/0168-583X(92)95839-J.
25. Nordlund, K (1995). "Simulación de dinámica molecular de rangos de iones en el rango de energía de 1–100 keV". Ciencia de materiales computacionales . 3 (4): 448–456. doi :10.1016/0927-0256(94)00085-Q.
26. Beardmore, Keith; Grønbech-Jensen, Niels (1998). "Esquema de dinámica molecular eficiente para el cálculo de perfiles de dopantes debido a la implantación de iones". Physical Review E . 57 (6): 7278–7287. arXiv : physics/9901054 . Bibcode :1998PhRvE..57.7278B. CiteSeerX 10.1.1.285.6727 . doi :10.1103/PhysRevE.57.7278. S2CID  13994369. 
27. Hobler, G. (2001). "Sobre el rango útil de aplicación de las simulaciones de dinámica molecular en la aproximación de la interacción de retroceso". Nuclear Instruments and Methods in Physics Research B . 180 (1–4): 203. Bibcode :2001NIMPB.180..203H. doi :10.1016/s0168-583x(01)00418-9.
28. Caturla, M. (1996). "Procesamiento de silicio mediante haz de iones a energías de keV: un estudio de dinámica molecular". Physical Review B . 54 (23): 16683–16695. Bibcode :1996PhRvB..5416683C. doi :10.1103/PhysRevB.54.16683. PMID  9985796.
29. Smith, R. (1997). "Simulación de dinámica molecular del bombardeo iónico de Ni {100} de 0,1 a 2 keV". Efectos de la radiación y defectos en sólidos . 141 : 425. doi :10.1080/10420159708211586.
30. Duvenbeck, A. (2007). "Promoción de electrones y fricción electrónica en cascadas de colisiones atómicas". New Journal of Physics . 9 (2): 38. Bibcode :2007NJPh....9...38D. doi : 10.1088/1367-2630/9/2/038 .
31. Hou, M. (2000). "Deposición de cúmulos de AuN en superficies de Au(111). I. Modelado a escala atómica". Physical Review B . 62 (4): 2825. Bibcode :2000PhRvB..62.2825H. doi :10.1103/PhysRevB.62.2825.
32. Bjorkas, C. (2009). "Evaluación de la relación entre la mezcla de haces de iones, el acoplamiento electrón-fonón y la producción de daños en Fe". Nuclear Instruments and Methods in Physics Research B . 267 (10): 1830. Bibcode :2009NIMPB.267.1830B. doi :10.1016/j.nimb.2009.03.080.
33. Pronnecke, S. (1991). "El efecto de la pérdida de energía electrónica en la dinámica de los picos térmicos en Cu" (PDF) . Journal of Materials Research . 6 (3): 483. Bibcode :1991JMatR...6..483P. doi :10.1557/jmr.1991.0483. S2CID  96618269.
34. Duffy, DM (2007). "Incluyendo los efectos de la detención electrónica y las interacciones electrón-ión en simulaciones de daño por radiación". Journal of Physics: Condensed Matter . 17 (1): 016207. Bibcode :2007JPCM...19a6207D. doi :10.1088/0953-8984/19/1/016207. S2CID  122777435.
35. Tamm, A. (2016). "Interacción electrón-fonón dentro de la dinámica molecular clásica". Physical Review B . 94 (1): 024305. Bibcode :2016PhRvB..94a4305L. doi :10.1103/PhysRevB.94.014305.
36. http://pdg.lbl.gov/2005/reviews/passagerpp.pdf ^{[ URL básica PDF ]}

Lectura adicional

• (Lindhard 1963) J. Lindhard, M. Scharff y HE Shiøtt. Conceptos de rango y rangos de iones pesados. Estera. Fys. Med. Dan. Vídeo. Selsk., 33(14):1, 1963.
• (Smith 1997) R. Smith (ed.), Colisiones atómicas y de iones en sólidos y superficies: teoría, simulación y aplicaciones, Cambridge University Press, Cambridge, Reino Unido, 1997.

Enlaces externos

• Cálculos de potencia de frenado y pérdida de energía en sólidos mediante el modelo MELF-GOS Archivado el 25 de septiembre de 2010 en Wayback Machine
• Un módulo basado en la Web para el alcance y la potencia de frenado en Nucleonica
• Paso de partículas cargadas a través de la materia
• Tablas de alcance y poder de frenado para electrones, protones e iones de helio
• Poder de frenado: gráficos y datos
• Penetración de partículas cargadas a través de la materia; notas de clase de E. Bonderup